Research Article, J Phys Res Appl Vol: 7 Issue: 2
A New Quantum Probability Theory, Quantum Information Functor and Quantum Gravity
Maziar Esfahanian*
Department of Mathematical Sciences, Polytechnic University of Turin, Turin, Italy
*Corresponding Author: Maziar Esfahanian
Department of Mathematical Sciences,
Polytechnic University of Turin, Turin, Italy;
E-mail: maziar.esfahanian@polito.it
Received date: 22 January, 2023, Manuscript No. JPRA-23-87672;
Editor assigned date: 25 January, 2023, PreQC No. JPRA-23-87672 (PQ);
Reviewed date: 08 February, 2023, QC No. JPRA-23-87672;
Revised date: 21 April, 2023, Manuscript No. JPRA-23-87672 (R);
Published date: 28 April, 2023, DOI: 10.4172/JPRA.1000028
Citation: Esfahanian M (2023) A New Quantum Probability Theory, Quantum Information Functor and Quantum Gravity. J Phys Res Appl 7:2.
Abstract
Quantum information theory is an important branch of theoretical physics with important experimental applications and is much richer than the classical one. Nonetheless, it seems that there is no precise description for it and people usually refer to some special aspects which show the difference between these two theories like, for instance, the no cloning theorem. Our aim here is to propose a new definition of quantum information theory by means of category theoretic tools and then show it can be more “natural” than classical information theory in some respect. This definition also suggests that loop quantum gravity and string theory are two shapes of a same theory of quantum gravity which are describable as two different conceptions of space time and space in a special mathematical structure. This mathematical structure is topos. In addition, we claim that within this point of view information is more fundamental than the concepts of space and space time in physics. We got inspired from the works of John Baez to work on this subject.
Keywords: Quantum information, Information theory, No cloning theorem, Topos theory, Space time, Loop quantum gravity, String theory
Introduction
Quantum information theory is a highly important branch of theoretical and experimental physics and is much richer than classical one [1]. A precise definition of this theory is needed to better understand many concepts and problems in theoretical physics. For instance Wigner’s friend problem which has been recently tackled by experimental physicists [2,3]. In the present paper we introduce a new notion of quantum probability theory and then by means of this new concept, we define quantum information theory as a functor from a special category which we call stringy information structure to the category spin foams.
This new perspective has some significant effects on our understanding of string theory and Loop Quantum Gravity (LQG) which usually are considered as two different approaches to the quantum gravity.
We try to show that either string theory or LQG can be considered as different approaches to the concepts of space and space time in the framework of topos theory. In 2014, Rodolfo Gambini and Jorge Pullin have shown the necessity of considering some specific non local interactions in quantum field theory similar to those that appear in string theory to avoid significant violations of Lorentz invariance [4]. This observation can show us the possible existence of some connection between LQG and string theory.
In addition, when we consider the notion of space, we can see that in both classical physics and general relativity physicists define space as a “set of points”. Indeed, the basic object used to define space in theoretical physics is a set which belongs to the category sets, of sets and usual maps, and then space is defined by considering elements of a set as points of the space. We call this notion of space an atomic notion.
This seems to suggest a more general approach in which the concept of space and consequently of space time is replaced by another notion based on topos theory, the category of toposes and geometric morphisms (topoi) which contains the atomic notion as a special case and, at the same time, is more useful and compatible with some general features of string theory. So, we believe that this more general characterization of space and space time is more appropriate for the formulation of a new theory which is compatible with both LQG and string theory. For this reason we reckon that this is a novel and insightful approach. Within our new quantum probability theory one can define the “chance that a superposition of states” occurs in quantum theory prior to an act of measurement. Moreover classical probability theory is a special case of this more general quantum one. In other words the quantum probability theory that we put forward is a probability theory describing a before and an after a measurement which is also quiet iconoclastic. The concept of superposition which is a weird concept in quantum theory will be a natural case in constructive mathematics and logic of topos theory which is equipped with heyting algebra. Historically, constructive or intuitionistic mathematics introduced by Brouwer with discarding the law of excluded middle [5]. Later Heyting provided an algebra which was consistent with Brouwer intuitionistic logic. In our point of view the law of excluded middle in logic implies the concept of position in classical physics and atomic notion of space in geometry. Despite of this, intuitionistic logic (constructive mathematics) which has discarded the law of excluded middle implies the concept of superposition in quantum physics and non-atomic notion of space in geometry. Thus, we are going to introduce a type of new quantum probability theory in a way that one can see the background logic of theory is intuitionistic logic.
To introduce our new quantum probability theory we use the concepts of partitions of a finite set and information structure which were recently introduced by Baudot and Bennequi [6]. The paper is organized as follows. In section 1, we just review the definition of partition and information structures and their related notions. In section 2 we put forward the notion of stringy information structure. In section 3, we suggest the new notion of quantum probability based on the concept of stringy information structure and mention the role of heyting algebra and topos theory in this new probability theory. Section 4 is the place that we define the quantum information functor. Finally, in the conclusion section we suggest some applications of our perspective to QFT, string theory and some problems in quantum theory. We also make some more general speculations, outlining our philosophical perspective about the interpretation of quantum mechanics in light of our general definition of quantum probability theory [7-9].
Materials and Methods
Partitions of a finite set and information structures
In this paper we consider measure theory as a known tool and refer the reader to Marzuoli, et al. Also, as far as topos theory is concerned, we refer the reader to Zafiris, et al.; Marzuoli, et al. We start from definition of a partition Zhang, et al.
Definition 1.1: Let (X, Σ, μ) be a probability distribution sp waciteh σ- algebra Σ and measure μ. A finite collection of measurable sets, α={A1, . . . , An} when n ∈ N and Ai ∈ Σ for i=1, . . . , n is called a finite partition if the following properties are fulfilled:
∀i = 1, . . . , n; μ (Ai)>0. for i ≠j;Ai ∩ Aj=∅. μ (X − (∪ ni=1 Ai)) = 0.
Remark 1: Each element of a partition is called a part of partition.
Definition 1.2: Let α={A1, . . . , An} and β={B1, . . . , Bm} are two partitions of the space X. We define the joint partition of these two partitions by:
α ∨ β:={Ai ∩ Bj|Ai ∈ α, Bj ∈ β}.
Definition 1.3: A finite partition γ is a refinement of a finite partition α whenever
∀C ∈ γ; ∃A ∈ α: C ⊂ A.
In this case also we say γ is “finer” than α.
Definition 1.4: Let Ω be a finite set. We define π (Ω) as the category of all finite partitions Ω of whose objects are finite partitions of Ω and there is an arrow between two objects X and Y, X → Y when X is finer than Y. When X is finer than Y we write Y ≤ X [10].
Remark 2: (π(Ω), V, {Ω}) has a monoid structure and {Ω} its unit element. Indeed we can easily verify that: for each
X ∈ π(Ω); X ∨ {Ω}={Ω} ∨ X=X
In fact it is the terminal object of the category π(Ω) since any partition is finer than {Ω} and we can write: For all X ∈ π(Ω); X→ {Ω}. For this reason {Ω} is also named “coarse” partition.
Notation 1: We denote the terminal object of a category C by 1C, so for example 1π(Ω)={Ω}, which is the coarse partition. In addition we denote the initial object of category C by 0C. Note that the existence of an initial object generally depends on finiteness of the set Ω.
For the category π(Ω) we write 0π(Ω)=Atm(Ω) which is the finest partition and call it atomic partition. It is defined as the partition consisting of 1-element sets only.
Definition 1.5: An information structure S is a full subcategory o f π(Ω) which satisfies the following properties:
• The partition {Ω} belongs to to obj(S).
• For every X, Y and Z in obj (S) if X → Y and X → Z then Y ∨ Z
belongs to obj(S)
To introduce our stringy information structure we need the notion of a sieve on an object of a category for which we refer the reader to Karakostas, et al.
Category of stringy information structures
Definition 1.5: S is a full subcategory of π(Ω) and since S contains {Ω}, it contains the identity morphism and from this it follows that the only sieve on the object {Ω} which will appear will be the maximal one. We introduce another notion, which is based on the concept of sieves in a category and the concept of minimal generator for the atomic partition which we define below. To this end we put forward the following two definitions.
Definition 2.1: Let Xi={{i, Ω-{i}} for i=1,...n be all the partitions of Ω with only two parts, one of which consists of one element only. We say that objects X1, X2, . . . ,Xm define a minimal set of generators for Atm(Ω) when X1 ∨ X2 ∨. . .∨ Xm=Atm(Ω) and, if we omit just one of them, say Xj for j=1, . . . ,m, the joint partition is not the atomic one.
Definition 2.2: Stringy information structure: A stringy information structure SinfS on Ω is a subcategory (not necessarily full) of π(Ω) such that:
• {Ω} ∈ obj (SinfS).
• Be a closed set under ∨ and contains only one minimal set of
generators <X1, . . . , Xm> of Atm(Ω).
• Mor(SinfS)-{Loops(identity morphisms)} be the minimal sieve on
object {Ω} which is generated by the arrows X1 → {Ω}, X2 →
{Ω}, . . . , Xm → {Ω}.
Remark 3: A sieve S is said to be generated by a family F of arrows contained in it if every arrow in S factors through an arrow in F [13].
Theorem 2.3: A stringy information structure is an information structure.
Proof: By definition 2.2, it is clear that a stringy information structure has the terminal element and also because of property b) of definition 2.2 automatically property (b) of definition 1.5 holds.
Remark 4: Clearly, an information structure is not a stringy information structure in general.
Since an information structure in definition 1.5 is based on the concept of full category and the existence of the identity of terminal object (i.e. a loop on the terminal object) is a fact there, this structure leads to the appearance of just maximal sieves on the terminal object. For this reason, from now on, we will refer to an information structure as a loopy information structure. So according to theorem 2.3 every stringy information structure is a loopy information structure.
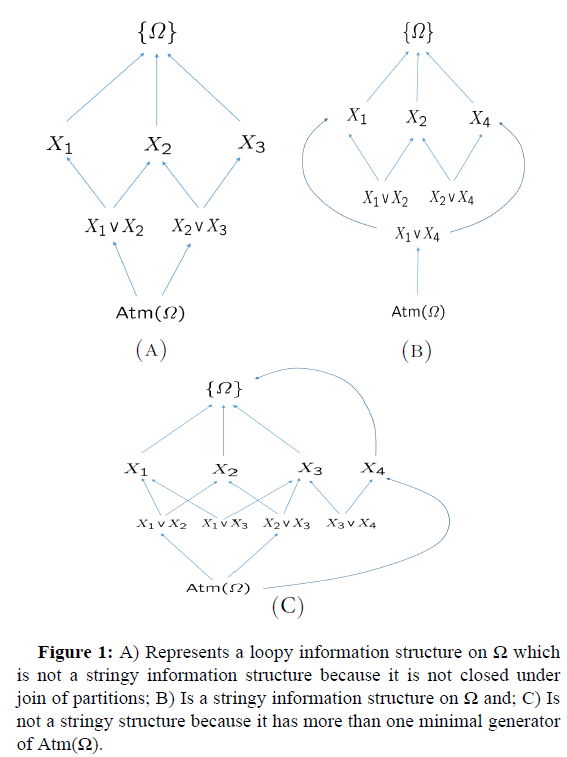
Example 2.4: Let Ω={1, 2, 3, 4}. In the Figure 1 below: Figure 1A represents a loopy information structure on Ω which is not a stringy information structure because it is not closed under join of partitions. Figure 1B is a stringy information structure on Ω and Figure 1C is not a stringy structure because it has more than one minimal generator of Atm(Ω).
Definition 2.5: Given finite sets X and Y, a stochastic map f: X~Y assigns a real number fyx to each pair x ∈ X and y ∈ Y in such a way that fixing any element x, the numbers fyx form a probability distribution Y.
Remark 5: A function f: X → Y can be seen as special case of a stochastic map when we look at it as a matrix of numbers fyx=δyf(x) where, δ is the kronecker delta [14].
Let Ω be a finite set, f: {Ω}~obj (SinfS) be a stochastic map and SinfS be a stringy information structure on Ω. From the property {Ω}=1π(Ω), it follows that f: {Ω}~obj (SinfS) is a probability distribution on obj(SinfS).
Definition 2.6: Let q: Ω~obj (SinfS1) and r: Ω~obj (SinfS2) be two probability distributions on obj (SinfS1) and obj(SinfS2), respectively. We say that a stochastic map p: obj (SinfS1)~obj (SinfS2) is a measure preserving function when p◦q=r.
We note that p can be a usual map too because we have seen in the above remark that it is possible to regard any usual function as a stochastic map.
Definition 2.7: We say that an ordered pair of (SinfS, q) is an informative stringy space if SinfS is a stringy information structure and q a probability distribution on obj(SinfS).
Notation 2: We denote the category of all informative stringy spaces and measure preserving maps among them by InfS.
Notation 3: Measure preserving maps play the role of measurements in quantum physics.
Meet of partitions, negation of a partition, quantized field (algebra) and new quantum probability
In part 1, we introduced the concept of partitions and their join. Here first of all we will define what the meet of partitions is, and then we shall introduce the new concepts of elementary and real quantized algebra which will help us to understand the measure theoretical background of our new definition of quantum probability based on the concept of stringy information structure.
Definition 3.1: Let X and Y be two partitions of a finite set Ω. The meet of X and Y is denoted by X ^ Y and defined as the finest partition which is less fine than both X and Y.
To compute the meet of two partitions we will use the graph theoretical method which is introduced in Mannone, et al. [15].
Example 3.2: Consider Ω={1, . . . , 4} and two of its partitions:
X4={{4}, {1, 2, 3}} X1 ∨ X2={{1}, {2}, {3, 4}}.
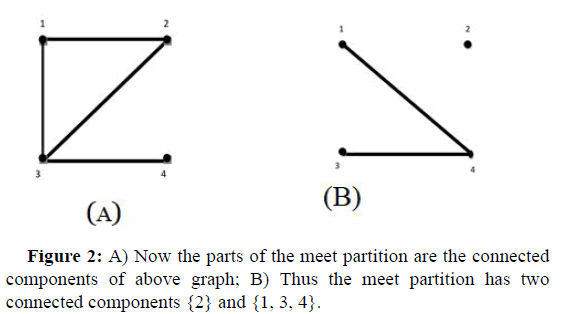
We associate a vertex with each element of Ω and draw a graph that has edges between each to vertices which are in a same part of at least one of partitions X4 ={{4, {1, 2, 3}} or X1 ∨ X2 ={{1}, {2}, {3, 4}}. So the graph is Figure 2A as like as in the Figure in next page. Now the parts of the meet partition are the connected components of above graph. So (X1 ∨ X2) ∧ X4={{1, 2, 3, 4}}={Ω}. Now consider partitions X1 ∨ X2={{1}, {2}, {3, 4}} and X2 ∨ X3={{2}, {3}, {1, 4}} and compute the meet partition for them. So we have: Figure 2B thus the meet partition has two connected components {2} and {1, 3, 4}, (X1 ∨ X2) ∧ (X2 ∨ X3)={{2}, {1, 3, 4}}=X2.
Definition 3.3: The implication partition X ⇒ Y of two partitions X and Y of a finite set Ω is the partition whose parts are the connected components of the graph obtained by associating a vertex with each element of Ω and joining by an edge only those pairs of vertices which are in a same part of Y but not in a same part of X (Figure 3).
Example 3.4: Consider Ω={1, 2, 3, 4} and these two partitions on it;
X4={{4}, {1, 2, 3}} and Y={{1, 2}, {3, 4}}.
For computing X4 ⇒ Y, following the above rules we draw the graph below and so we have the connected components: {1}, {2}, {3,4}. Thus we have (X4 ⇒ Y)={{1}, {2}, {3,4}}.
Definition 3.5: The negation or pseudo complement of a partition X of a finite set Ω is denoted by ¬X and defined as the partition X ⇒ {Ω}.
According to what we discussed above, one can easily see that the sextuple (π(Ω), ∨,∧ ⇒,¬,≼) is a non-distributive heyting algebra whose bottom element is {Ω} and top element is Atm(Ω), while (π(Ω), ∨, ∧, ⇒, ¬, ≼OP) also is a heyting algebra whose bott, m element is Atm(Ω) and top element is {Ω}. Where relation ≼OP is defined as the converse relation of “which means;
Y ≼OP X if and only if X ≼OP Y.
When X ≼OP Y we say Y is coarser than X.
We recall that Y ≼ X means partition X is finer than Y and so X ≼OP Y means that
Y is coarser than X if and only if X is finer than Y (Y ≼ X).
For some technical reasons to show compatibility of our new quantum probability with classical one we also need to use (π(Ω), ∨, ∧, ⇒, ¬, ≼OP).
We note that ∨ of (π(Ω), ∨, ∧, ⇒, ¬, ≼) plays the role of the meet in the Heyting algebra (π(Ω), ∨, ∧, ⇒, ¬, ≼OP) and ∧ of (π(Ω), ∨, ∧, ⇒, ¬, ≼) plays the role of the joint in the Heyting algebra (π(Ω), ∨, ∧, ⇒, ¬, ≼OP).
Quantized algebra (field)
Definition 3.6: An elementary quantized algebra of sets on Ω is a non-empty collection QA of subsets of pow(Ω), such that:
• {Ω} ∈ QA
• Q is closed under operator V: Let X ⊆ Pow(Ω) and Y⊆ Pow(Ω) we
define X ∨ Y:={A ∩ B|A ∈ X, B ∈ Y}on Pow(Ω).
• Q is closed under the power complement operation w dheifcihn edis:
if X ∈ QA then XPc:={Ac|A ∈ X} ∈ QA.
Now we can show that an algebra is a special case of an elementary quantized algebra.
Theorem 3.7: Let QA be an elementary quantized algebra, which contains only the subsets X ⊂ Pow(Ω) that chard (X)=1, then QA induces algebra A on Ω.
Proof: Since card ({Ω})=1, we have no problem with its presence in QA. Let X and Y be in QA so card(X)=card(Y)=1 by assumption. Let X={A} and Y={B} where A and B are subsets of Ω. We then have X ∨ Y={A ∩ B} ∈ QA by definition of QA. So if A and B are subsets of Ω such that {A}, {B} ∈ QA we construct A={Ai ⊂ Ω|{Ai} ∈ QA}. Now let Ai and Aj be elements of A so that {Ai} and {Aj} are elements of QA. Thus, by definition {Ai} ∨ {Aj}={Ai ∩ Aj} ∈ QA. So we have Ai ∩ Aj ∈ A. Now let Ai ∈ A, so {Ai} ∈ QA and {Ai}Pc ={Aic} ∈ QA. (By definition) thus Aic ∈ A and, because of Demorgan’s Law we have Ai ∪ Aj ∈ A. Finally, {Ω}Pc={Ωc}={∅} ∈ QA so we have ∅ ∈ A. Thus A is algebra on Ω.
Definition 3.8: A real quantized algebra on Ω is a non-empty collection RQA of subsets of Pow(Ω) such that:
•{Ω}∈ RQA
•RQA closed under V (joint of the subsets of Pow(Ω)).
Theorem 3.9: Let Ω be a finite set. π(Ω) is a real quantized algebra.
Proof: Clearly {Ω}, being a partition, belongs to π(Ω) and, by definition, π(Ω) is closed under the joint operation between partitions.
Remark 6: Every elementary quantized algebra is a real quantized algebra which, in addition, includes the complement operation. Therefore any probability theory built on such a structure contains the notion of incompatibility of some events induced by the mathematical concept of complementarity between sets.
We want to build a probability theory which is suited to describing quantum super positions. To this end choose as mathematical framework for defining our notion of quantum probability not an elementary quantized algebra but rather a real one as the universe set. According to the definition of a stringy information structure, it is a real quantized Algebra and also it is a subcategory of π(Ω). We define our quantum probability on a stringy information structure, because of its nice categorical properties and the existence of a heyting algebra.
Definition 3.10: Suppose Ω is a finite set and SinfS is a stringy information structure equipped with same converse relation ≼OP of (π(Ω), ∨, ∧, ⇒, ¬, ≼OP). We define the quantum probability of two partitions X and Y of (obj(SinfS), ≼OP) as follows:
QP (X|Y):=P (X ∨ Y)/P (Y ).
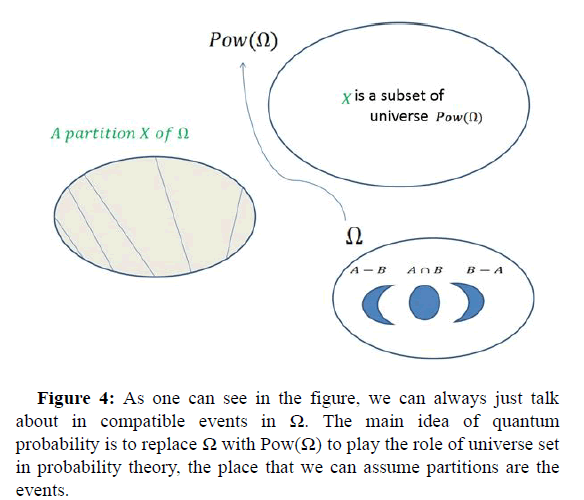
Here, we try to illustrate the main point of quantum probability in Figure 4.
Remark 7: We used converse relation ≼OP in the definition of Quantum Probability (QP) because we wanted to adapt the order with what we have in classical probability theory which has the empty set in the bottom and the universe set at the top of the order of classical algebra of subsets.
Properties of quantum probability theory
• If Y={Ω} the top element of (SinfS, ≼) then we have,
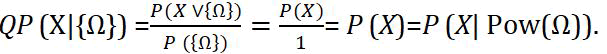
(Compatibility of quantum probability theory with classical probability theory).
• QP never vanishes for any pairs of non-empty partitions. It means
there are no incompatible events in quantum probability theory. This
property allows us to talk about quantum superposition in a natural
way, consistently with the way this notion is defined in physics.
• Let Y = Atm(Ω) the bottom element of (SinfS, ≼) then we have:
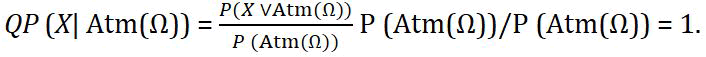
• We note that, for instance, one can define the probability of a o fs eat Ω as which is finite because we have no empty partition so th atthe cardinality of a partition is never zero.
Results and Discussion
Quantum information functor and quantum gravity
Definition 4.1: Let Ω be a finite set and SinfS a stringy Information Structure equipped with same converse relation ≼OP of (π(Ω), ∨, ∧, ⇒, ¬, ≼OP).
We define a quantum information functor on Ω at a partition X as the following functor.
QInf FX: SinfS → Spinfoamsn
(Xi → X) ›→ Conv ({QP (Xi|X)} ∪ {0}),
Where (Xi → X) is the refinement arrow while by conv ({QP (Xi| X)} ∪ {0}) we mean the convex hull of {QP(Xi|X) ∪ {0} and spinfoamsn denotes the category of n-dimensional spin foams (morphisms) and their boundaries, which are (n-1)-dimensional spin networks.
Definition 4.2: Classical information theory is a special case which arises when we put X={Ω} in above definition.
Remark 8: We put {0} in the definition to make it compatible with classical information theory based on the notion of classical probability.
Although we have not enough information about conv ({QP (Xi|X)} ∪ {0}) yet, here we conjecture that it represents a full subcategory of spin foams with a monoidal structure. A formal proof of this statement is work in progress.
Definition 4.3: A Quantum Information Theory (QIT) on a finite set Ω is the category QIT of all functors QInf FX: SinfS spin foamsn, for all partitions X of Ω, and natural transformations between them.
It is known that a spinfoam is a kind of set and so the category of spinfoams is a subcategory of the category sets. We denote by ℇ=(C, sets) the category of all functors from category to category of sets is a topos when is a small category. Thus, QIT=(SinfS, spinfoamsn) is a topos (Table 1). Of course when we change our stringy information structure we arrive at another QIT on our universe set and consequently another topos will emerge. Therefore, in our category theoretic perspective quantum information theory is the study of the category topoi of toposes which we constructed in this text.
| Quantum probability | General relativity | Quantum theory | |
|---|---|---|---|
| Philosophical perspective | Neo-realism (superposition as aspects of being which looks like positions) | Ontology is equivalent to epistemology (mass determines the geometry of space) | Ontology is equivalent to epistemology (reduction of superposition to position) |
| Aspects of being | Partitions in a stringy information structure (states) | (n-1)-dimensional manifold (space) | Hilbert space (states) |
| Aspects of becoming | Refinements | Cobordism between (n-1)-dimensional manifolds (space time) | Operator between Hilbert spaces (process) |
| Aspects of interacting | Factoring some arrows through other arrows | Composition of cobordisms | Composition of operators |
| Aspects of stability | Loops | Identity cobordism | Identity operator |
Table 1: Analogy among quantum probability, general relativity and quantum theory.
Conclusion
We know about the idea of strings as one-dimensional objects which play in string theory the role of zero dimensional particles in Quantum Field Theory (QFT), and the notion of Dirichlet branes as hypersurfaces where open strings can end. It sounds that this increase in the dimension of the fundamental object when going from QFT to string theory calls for a more general categorical setting which is more suitable for a consistent formulation of a quantum gravity theory. More precisely, in terms of Baez’s concept of “aspects of being and becoming”, we can say that Dirichlet Branes are aspects of being. When particles are replaced by strings, it is probably appropriate to that of a non global object. This in turn would lead to a generalization of the notion of a Dirichlet Brane to a new geometrical entity which instead of allowed end points for open strings consists of “allowed non global generalizations of end points for open strings”.
Let us recall at this point that a non global element in a topos (or generally in a category) is an arrow whose domain is not a terminal object. So these elements do not behave as points of a connected space, which are global elements in categorical framework, since they can be reached from any other points by a path.
This suggested refinement of the notion of Dirichlet Branes and the content of this paper may support the necessity of giving up the atomic notion of space and space time in favor of a new concept which naturally emerges in our framework of topos, in which quantum information turns out to be more fundamental than space and spacetime themselves.
In addition, in our perspective, we can see quantum information theory is more natural than the classical one, because classical information arises when we restrict the quantum information functor to the coarsest partition {Ω} and arrive to the functor
QInf F{Ω}: SinfS → spin foamsn
(Xi → {Ω}) ›→ conv ({QP (Xi|{Ω})} ∪ {0}),
It means we have an information theory based on a probability theory associates a probability also with quantum states prior to any act of measurement, with the notions that we introduced in this paper. In this way, we can see logic becomes probability theory and then with defining quantum information functor we can see logic becomes information and information becomes space, space time and mechanics, in special case quantum mechanics.
Moreover, with our quantum probability theory, it may be possible to reformulate some deep open questions such as Wigner’s friend problem which is about quantum measurement in an ultimate observer-independent theory.
Let us end this concluding section by some more general comments of philosophical nature about the concepts which we dealt with in this paper.
Topological quantum field theory, as a toy model of string theory in a categorical framework, is a functor from the category n cobs of ndimensional cobordisms to the category Hilbs of Hilbert spaces (objects) and linear operator between them (morphisms).
Let us quote from John Baez: “Space and states are aspects of being and space time and processes are aspects of becoming”.
Let us summarize some categorical analogues of general relativity and quantum theory similarly to what Baez did in with add some analogues of quantum information theory and also aspects of interacting.
Neo-realism is the conceptual consequence of the fact that, from a categorical perspective, a physical theory expressed in a topos looks like classical physics described in the topos of sets.
If we want to define quantum information theory based on our definition of quantum probability we should accept the position of neo-realists. This iconoclastic idea of talking about partitions as states and quantum probability will remove the weirdness of quantum theory and quantum information theory, even if our theory is a toy model of a more general and rich theory of information.
Acknowledgment
This work is part of my research program as PhD student of the doctorate school in Pure and applied in mathematics at Turin polytechnic. I would like to thank Dr. B.L. Cerchiai and Prof. M. Trigiante for useful discussions.
References
- Freedman MH (2001) Quantum computation and the localization of modular functors. Found Comput Math 1:183-204.
- Freedman MH, Larsen M, Wang Z (2002) A modular functor which is universal for quantum computation. Comput Math Phys 227:605-622.
- Ghafari F, Tischler N, Di Franco C, Thompson J, Gu M, et al. (2019) Interfering trajectories in experimental quantum enhanced stochastic simulation. Nat Commun 10:1630.
[Crossref] [Google Scholar] [PubMed]
- Gambini R, Pullin J (2014) Emergence of string like physics from Lorentz invariance in loop quantum gravity. Int J Mod Phys D 23:1442023.
- DiVincenzo DP (2000) The physical implementation of quantum computation. Progress of Physics 48:771-783.
- Marzuoli A, Rasetti M (2002) Spin network quantum simulator. Phys Lette A 306:79-87.
- Zafiris E (2010) Boolean information sieves: A local to global approach to quantum information. Int J Gen Syst 39:873-895.
- Marzuoli A, Rasetti M (2005) Computing spin networks. Ann Phys 318:345-407.
- Zhang Y, Kauffman LH (2008) Topological like features in diagrammatical quantum circuits. Quantum Inf Process 7:3-2.
- Rasetti M (2010) Topology, formal languages and quantum information. Milan J Math 78:289-317.
[Crossref] [Google Scholar] [PubMed]
- Pavlovic D (2011) Relating toy models of quantum computation: Comprehension, complementarity and dagger mix autonomous categories. Electron Notes Theor Comput Sci 270:121-139.
- Karakostas V, Zafiris E (2017) Contextual semantics in quantum mechanics from a categorical point of view. Synthese 194:847-886.
- Panangaden P, Paquette EO (2011) A categorical presentation of quantum computation with anyons. New Stru Phys 983-1025.
- Baianu IC, Brown R, Glazebrook JF (2007) A non-Abelian, categorical ontology of space times and quantum gravity. Axiomathes 17:353-408.
- Mannone M, Seidita V, Chella A (2022) Categories, quantum computing, and swarm robotics: A case study. Mathematics 10:372.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi