Research Article, Int J Cardiovasc Res Vol: 4 Issue: 4
Application of the Reservoir Wave Approach to the Renal Circulation
| Kristen C Handkamer2, Lindsay M Burrowes2, J Christopher Bouwmeester2, Ryan Richardet2, Rodger Loutzenhiser2,3, and John V Tyberg1-3* | |
| 1Departments of Cardiac Sciences, University of Calgary, Alberta, Canada | |
| 2Department of Physiology and Pharmacology, University of Calgary, Alberta,Canada | |
| 3Libin Cardiovascular Institute of Alberta, University of Calgary, Alberta, Canada | |
| Corresponding author : John V Tyberg, MD, PhD University of Calgary Faculty of Medicine, 3280 Hospital Drive NW, HRIC GAA18, Calgary, Alberta, Canada Tel: +403-220-6866 E-mail: jtyberg@ucalgary.ca |
|
| Received: January 09, 2015 Accepted: March 26, 2015 Published: March 28, 2015 | |
| Citation: Handkamer KC, Burrowes LM, Bouwmeester JC, Richardet R, Loutzenhiser R, et al. (2015) Application of the Reservoir-Wave Approach to the Renal Circulation. J Cardiovasc Res 4:4. doi:10.4172/2324-8602.1000214 |
Abstract
Application of the Reservoir Wave Approach to the Renal Circulation
In this pilot study of the renal circulation we applied the reservoirwave approach, a time-domain method for the analysis of arterial pressure and flow that defines the magnitudes of the series resistances that account for the total vascular resistance of an organ. Renal and systemic pressures and flows were measured in anesthetized dogs. Unilateral infusions of angiotensin II (ANG II) or endothelin-1 (ET-1) decreased renal conductance by 30% and 50%, respectively. These decreases in conductance were accounted for by increases in large-artery resistances by 83% and 79%, respectively, and by increases in microcirculatory resistances by 171% and 275%, respectively. Reservoir resistance did not change with ANG II, but increased by 36% with ET-1. P∞ (the theoretical non-zero pressure at which flow ceases) increased from 28.2 ± 4.5 to 37.0 ± 5.7 mmHg (P<0.01) with ANG II and increased from 32.7 ± 5.9 to 43.7 ± 3.3 mmHg (P<0.05) with ET-1. The marked increase in P∞, particularly with ET-1, suggests a preferential decrease in diastolic renal blood flow. The reservoir-wave approach may provide a useful tool for studying the unique aspects of the renal circulation in health and disease.
Keywords: Venous resistances; Renal circulation; Renal diseases
Keywords |
|
| Venous resistances; Renal circulation; Renal diseases | |
Introduction |
|
| Hypertension is a major risk factor for chronic kidney disease (CKD) and its subsequent progression into end-stage renal disease (ESRD) [1,2]; the risk for ESRD increases by 6.7% with every 10 mmHg rise in baseline systolic blood pressure [3]. Hypertension and renal disease can each be the cause or the consequence of the other and thus a better understanding of the interrelationship of blood pressure and the kidney is needed [4]. | |
| A decade ago, Wang et al. proposed a novel analysis of arterial pressure and flow waveforms, the reservoir-wave approach [5]. In essence, it involved a reinvention of Frank’s 2-element Windkessel [6], modified to include a non-zero asymptotic pressure (P∞); it represents measured pressure as the instantaneous summation of wave-related excess pressure and volume-related reservoir pressure [5]. Since its inception, the reservoir-wave approach [5,7] has been successfully applied to the systemic [5,8-11] and pulmonary circulations [12-14]. It has never been applied to the renal circulation, despite the importance and unique characteristics of that circulation. | |
| The primary purpose of this pilot study was to develop a methodology that would allow for the application of the reservoirwave approach to the renal circulation. In doing so, we examined how a unilateral, renal arterial infusion of vasoconstrictors altered conductance, P∞, and series resistances. We compared those parameters to those calculated from the previous, ipsilateral control observation and also to those calculated from concurrent observations of the non-infused contralateral kidney. We used two vasoconstrictors, endothelin-1 (ET-1) and angiotensin II (ANG II), both of which are potent, naturally occurring proteins [15,16]. Similar to ET-1, ANG II has been implicated in both CKD and renal hypertension. While it is agreed that ET-1 generally functions as a vasoconstrictor, various investigators have reached different conclusions as to its relative afferent and efferent arteriolar effects [3,17-21]. Loutzenhiser et al. [18] Fretschner et al. [21] and Inscho et al. [17] have all reported a preferential constriction of the afferent arteriole following ET-1 administration. ANG II was selected, as relatively equal effects on both the pre- and post-glomerular resistance vessels have been reported [22]. The reservoir-wave approach to the renal circulation suggests that ET-1 and ANG II decreases total conductance by raising P∞ and, therefore, by increasing microcirculatory/venous resistance. | |
Materials and Methods |
|
| All experimental protocols were approved by the Animal Care Committee of the University of Calgary and were consistent with the criteria of the Canadian Council on Animal Care and the American Physiological Society. | |
| Fourteen healthy male dogs (18-32 kg) were surgically instrumented. Two days before the experiment, the dogs were pretreated with a cyclo-oxygenase inhibitor (ibuprofen; 12.5 mg/kg bolus) to reduce prostaglandin formation and were given additional table salt in their daily diet (2 g NaCl per day) to suppress the renin angiotensin system (RAS) [23]. Food and water were withheld on the morning of the experiment. An ACE inhibitor (enalaprilat; 0.02 mg/ kg/h i.v.) was given after anesthesia to further reduce endogenous ANG II levels [24,25]. | |
| Anesthesia was induced with sodium thiopental (25 mg/kg, i.v. bolus) and a cuffed endotracheal tube was inserted. The animal was placed in a supine position and ventilated (3:2::oxygen:nitrous oxide mixture) using a constant-volume respirator (Harvard Apparatus, Holliston, MA) adjusted to a tidal volume of 15-19 ml/kg and a rate of 16-18 breaths per minute [26]. A 5-mg induction dose of fentanyl citrate was administered and anesthesia was maintained with a fentanyl infusion (0.20 mg/kg/h), in conjunction with midazolam (0.05 mg/kg/h). Body temperature was maintained at 37°C using a circulating water blanket and monitored throughout. Fluids (5% dextrose in normal saline) were administered as a constant drip via the left jugular vein. A standard 3-lead ECG was recorded and lidocaine (3 bolus intravenous doses of 1 mg/kg, 5 minutes apart, followed by a continual drip at 1 mg/ml) was administered as necessary to suppress arrhythmias. Based on regular blood-gas analyses, the respirator was adjusted as necessary to achieve a pH between 7.38 and 7.40, a PO2 greater than 120 mmHg and a PCO2 of 35-45 mmHg. A midline thoracotomy and laparotomy were performed and highfidelity catheter-tip manometers (Scisense Inc., London, ON) were placed in the left ventricle, ascending aorta, and in the aorta adjacent to the renal arteries (as a surrogate for renal artery pressure and to avoid obstructing the artery). Fluid-filled catheters and conventional transducers were used to measure pressure in the right renal vein and inferior vena cava (IVC). Ultrasonic flow probes (Transonic Systems Inc., Ithaca, NY) were placed on the ascending aorta and on both renal arteries. A drug-infusing catheter, fashioned by creating perforations just proximal to the occluded end of a length of polyethylene tubing (PE 50), was advanced into the left renal artery, via the left femoral artery. Both ureters were catheterized, which allowed unobstructed urine flow. | |
| Starting with the sixth experiment, to obviate the surgical stress of the midline laparotomy, a bilateral flank approach was developed for renal instrumentation. This involved an approximately 10-cm surgical incision while the animal was in the lateral decubitus position, allowing access to the renal artery for placement of the ultrasonic flow probes and ensuring proper location of the infusion catheter. Following this procedure, the incisions were re-approximated to minimize fluid loss and the animal was returned to a supine position. Starting with the twelfth experiment, to reduce surgical stress further we discontinued the midline-thoracotomy. We sacrificed the measurement of ascending aortic flow but employed a Swan-Ganz, triple-lumen catheter to determine the downstream left atrial pressure and measure cardiac output. Catheter placement was confirmed using fluoroscopy. | |
| Of the 14 animals surgically instrumented, data were successfully collected from 9. Two animals died prior to the completion of the instrumentation (Experiments 5 and 6) and data were discarded from Experiment 1 because of a tachycardia. Furthermore, data were discarded from an additional two animals (Experiments 7 and 11) because renal flow could not be altered by either vasoconstrictors or vasodilators, perhaps indicating catheter misplacement or other technical malfunction. | |
| Pharmacologic interventions | |
| Because vasoconstriction induced by ET-1 has been shown to be persistent [18], ANG II was always given first. ANG II (20 ng/kg/ min) and ET-1 (5 ng/kg/min) were dissolved in saline and infused continuously at doses sufficient to reduce renal arterial flow by approximately 50%. A 20-min stabilization period was allowed before data were collected. To eliminate respiratory variation, the ventilator was turned off at end-expiration for 10-s intervals to collect data. After ANG II administration, a 20-min recovery/wash-out period was allowed. Then a control recording was repeated to document any alteration in baseline values. During this period only saline (2 ml/min) was infused into the renal artery. Following the completion of the experiment and while the animal was still under full general anesthesia, it was euthanized with an IV bolus of saturated KCl. | |
| Analysis of hemodynamic data | |
| Based on the assumption that the rate of change of reservoir pressure (PRes) should be proportional to the rate of change of volume, Wang et al. [5] defined PRes according to the following equation (modified for the renal artery). | |
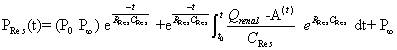 |
|
| t0 and P0 are the time and pressure at the onset of ejection; P∞ is the extrapolated value of the exponential decline in arterial diastolic pressure and, theoretically, the pressure at which renal arterial outflow would stop; RRes and CRes are the resistance and compliance of the reservoir; and Q Renal – A is renal artery blood flow. | |
| An example of the application of the reservoir-wave approach to the renal circulation is shown in Figure 1. The waveform of aortic pressure waveform measured at the level of the renal arteries and its mean value are shown. Also shown is the waveform of reservoir pressure and its mean value [5]. A solid horizontal line indicates the value of P∞. | |
| Figure 1: An example of the application of the reservoir-wave approach to the renal circulation. An aortic pressure waveform (top black solid line) recorded at the level of the renal arteries is shown as well as its mean value (black dashed line). Also shown is the waveform of reservoir pressure (red solid line) as calculated from pressure and renal arterial flow (not shown) and its mean value (red dashed line). The difference between measured aortic pressure and reservoir pressure is excess pressure; its rapid rise at the beginning of systole is due primarily to the forward-going compression wave generated by the LV. The dashed blue horizontal line indicates the value of P∞. Inferior vena caval pressure (PIVC) waveform is indicated by the bottom black solid line; its mean value, by the black dashed line. As shown on the right, these values allow total renal vascular resistance (RVR) to be divided into series segmental resistances: renal large-artery resistance (RLrg-A), renal arterial reservoir resistance (Rres), and microcirculatory/ venous resistance Rmicro/ven. | |
| The mean values of each waveform and P∞ correspond to the bar graph on the right side of Figure 1. These values allow total renal vascular resistance [(mean arterial pressure – mean IVC pressure)/ mean renal arterial flow] to be divided into series segmental resistances: renal large-artery resistance, renal arterial reservoir resistance, and microcirculatory/venous resistance [9]. (Because renal venous blood flow was not measured, it was not possible to calculate venous resistance and, thereby, to identify microcirculatory resistance as distinct from venous resistance.) | |
| P∞ was determined by plotting renal artery pressure against renal flow during the last 140 ms of diastole [27]; the linear extrapolation of this relationship resulted in a positive-pressure intercept at zero flow. [We assumed that resistance was linear and constant during this interval. Renal autoregulation implies changing resistance but the delay in the onset of pressure-dependent renal vasodilation in the rat has been estimated to be 0.4 to 1.0 seconds [28,29] too long to affect this determination.] This zero-flow pressure was calculated individually for each beat during the 10-s data-collection period and the results were averaged. Defining this zero-flow pressure to be equivalent to P∞, we then inserted it as a known constant into the direct search algorithm (fminsearch) [5]. We then proceeded to use the algorithm to minimize the mean-squared error between the measured and the iteratively calculated values of reservoir pressure during diastole and, thus, to determine reservoir pressure throughout the cardiac cycle. | |
Statistical Analysis |
|
| Data are presented as means ± SEM. Data were analyzed using SigmaPlot for Windows Version 12.3 (Systat Software Inc., San Jose, CA). Interventional data from both the left and right kidney were assessed against baseline data using a two-tailed, paired t-test in the cases where data passed a Shapiro-Wilk normality test. Where normality failed, we used a non-parametric Wilcoxon signed-rank test. An asterisk was placed next to the SEM values calculated with the Wilcoxon signed-rank test. Wilcoxon signed-rank tests were also employed to examine whether the kidney receiving the intervention differed from the contra-lateral kidney. P values less than 0.05 were taken to be significant. | |
Results |
|
| Conductance | |
| Conductance, the reciprocal of resistance, denotes the rate of blood flow that the kidney will accept for a given arterio-venous pressure difference (Figure 2) shows that both ANG II and ET-1 decreased the conductance of the infused kidney, from 3.14 ± 0.59 to 2.21 ± 0.35 mL/min/mmHg (P <0.01) and from 2.51 ± 0.36 to 1.25 ± 0.29 mL/min/mmHg (P<0.01), respectively. Having determined the degree to which ANG II and ET-1 decreased conductance, we used the reservoir-wave approach to define how these conductance decreases were mediated by changes in the series resistance components. | |
| Figure 2: Pooled data showing the change in absolute conductances of the left (infused) kidney, before (dark gray) and after (light gray) infusion of ANG II (left panel) and ET-1 (right panel). | |
| P∞ | |
| The value of P∞ is critical to determining the values of reservoir and microcirculatory/venous resistances, as shown in Figure 1. Figure 3 shows that ANG II and ET-1 increased the P∞ of the infused kidney from 28.6 ± 4.5 to 36.8 ± 6.0 mmHg (P<0.01) and from 33.1 ± 3.8 to 43.6 ± 3.0 mmHg (P<0.05), respectively. | |
| Figure 3: Pooled data showing the differences in P∞ (mmHg) values before (dark gray) and after (light gray) infusion of ANG II (left panel) and ET-1 (right panel). | |
| Serial resistance changes | |
| Figure 4 shows changes in pooled mean resistance components with ANG II (left) and ET-1 (right). Note that the total heights of the columns (total renal vascular resistance) vary reciprocally with the heights of the conductance columns (Figure 2). Note also that the increases in the heights of the microcirculatory/venous columns (light gray, bottom) are approximately equivalent to the increases in the respective P∞ columns (Figure 3), indicating that the increases in microcirculatory/venous resistances account for the decreases in conductance (Figure 2). With ANG II administration, largeartery resistance increased by 83% (P<0.05), reservoir resistance did not change, and microcirculatory/venous resistance increased by 171% (P<0.05*). With ET-1 administration, large-artery resistance increased by 79% (P<0.05*), reservoir resistance increased by 36% (P<0.05), and microcirculatory/venous resistance increased by 275% (P<0.01). | |
| Figure 4: Changes in pooled mean resistances due to ANG II (left) and ET-1 (right). With ANG II administration (left panel), large-artery resistance (dark gray, top) increased by 83% (P < 0.05), reservoir resistance (middle) did not change, and microcirculatory/venous resistance (light gray, bottom) increased by 171% (P < 0.05*). With ET-1 administration (right panel), large-artery resistance increased by 79% (P < 0.05*), reservoir resistance increased by 36% (P < 0.05), and microcirculatory/venous resistance increased by 275% (P < 0.01). Note that the increases in the heights of the microcirculatory/venous columns are approximately proportional to the increases in the respective P8 columns suggesting that the increases in microcirculatory/venous resistances account for the decreases in conductance. | |
| Change in renal blood flow vs change in P∞ | |
| ANG II and ET-1 appear to have decreased renal blood flow in proportion to the increase in P∞. In Figure 5, the decrease in renal blood flow (%) is plotted against the increase in P∞ (mmHg) for leftkidney infusions of ANG II (top) and ET-1 (bottom). Black solid circles indicate the results of individual experiments; the circles with SEM error bars indicate the average results. Straight lines were arbitrarily drawn from the origin through the points to the x-axis. ANG II decreased renal blood flow to 62.8 ± 3.5% of the control value and increased P∞ by 10.2 ± 3.6 mmHg; by interpolation, a 50% reduction in flow was associated with an increase in P∞ of 13.6 mmHg. ET-1 decreased renal blood flow to only 37.1 ± 4.1% of the control value and increased P∞ by 14.5 ± 2.7 mmHg; by interpolation, a 50% reduction in flow was associated with an increase in P∞ of 11.5 mmHg. (For ANG II, if the experiment in which the increase in P∞ was negligible [i.e., the left-most, almost vertical line in the bottom panel] is considered to be an outlier and ignored, the results of the two interventions become very similar: a 50% reduction in flow is associated with an increase in P∞ of ~12.0 mmHg with the administration of either vasoconstrictor). | |
| Figure 5: The reduction in left kidney flow (percent control) versus the change in arterial P∞ (mmHg) during the infusion of ANG II (top panel) and ET-1 (bottom panel). For each individual experiment, the percentage reduction in flow was plotted against the increase in P∞ and shown by a filled circle; arbitrarily, a straight line was then drawn from the origin (flow = 100% of control flow; ΔP∞ = 0 mHg) through the filled circle to the zero-flow x-axis. Pooled mean values (± SEM) of flow reduction and ΔP∞ are given by the open circle; the bold dashed line was drawn through that point. On average, ANG II reduced flow to 62.8 ± 3.5% of the control value and raised P8 by 10.2 ± 3.6 mmHg; interpolation revealed that a 50% reduction in control renal flow was associated with an increase in P∞ of approximately 13.5 mmHg. ET-1 reduced flow to only 37.1 ± 4.1% of the control value and raised P8 by 14.5 ± 2.7 mmHg; interpolation revealed that a 50% reduction in control renal flow was associated with an increase in P∞ of approximately 11.3 mmHg. | |
Discussion |
|
| Application of the reservoir-wave approach | |
| This pilot study is the first application of the reservoir-wave approach to the renal circulation. The results suggest that the increase in total renal resistance was specifically due to an increase in microcirculatory/venous resistance, which was due to an increased renal arterial P∞. | |
| Conductance | |
| Our methodology confirmed that conductance decreased with ANG II and ET-1 administration. ANG II and ET-1 reduced conductance by 36% and 50% of the control values, respectively (Figure 2). The reservoir-wave approach suggested that this conductance decrease was mediated by changes in the series resistance components (in particular, the increase in microcirculatory/venous resistance). Given the potency of ET-1 and its seeming predilection to constrict afferent arterioles [17,18], to find that ET-1 increased microcirculatory/venous resistance more than ANG II was not unexpected. | |
| P∞ | |
| As diastolic pressure decreases exponentially, Wang et al. observed that it approaches a non-zero value (i.e., P∞), which they reasoned would be the arterial pressure at which flow out of the aortic reservoir would stop [5]. If the P∞ of peripheral circulations were substantially lower, this would explain diastolic flow to those circulations. | |
| The reservoir-wave approach appears to offer new insights with respect to the mechanisms of diastolic arterial flow. Whereas there is negligible diastolic flow in the proximal aorta because there is no upstream compliance, diastolic flow is substantial in cerebral, coronary, intestinal, and renal arteries. We suggest that this diastolic flow represents a redistribution of blood volume between upstream and downstream capacitances, i.e., between the proximal aorta and the vital organs for which this diastolic flow appears to be critical. Because this flow is driven by the difference between reservoir pressure and P∞, we have termed this reservoir flow. | |
| The increase in P∞ following the intra-renal arterial infusion of vasoconstrictors (ET-1 and ANG II) would seem to have been anticipated by Burton almost 6 decades age [30]. Burton described the concept of active tension due to the contraction of smooth muscle fibers within the vessel wall, which is thus subject to the influence of vasoactive substances such as ANG II and ET-1 [30]. As blood pressure decreases, vessel diameter decreases until the distending force of the pressure is equaled by the opposing active tension; a further decrease in pressure results in complete vessel closure [30]. Burton labeled the pressure at which point flow theoretically ceases as the critical closing pressure (analogous to P∞) and suggested that it would be a useful index of vascular tone [30]. As indicated above, the value of P∞ is critical in the reservoir-wave approach in that it distinguishes between reservoir and microcirculatory/venous resistances. As might have been expected, the reservoir-wave approach suggested that ANG II and ET-1 increased the P∞ of the infused kidney (Figure 3). | |
Comparison of the Infused to the Non-infused Kidney |
|
| Both ET-1 and ANG II were administered via a purpose-built infusion catheter in the left renal artery. Had that catheter not delivered the agents selectively or had the agents been given in excess such that they would pass through the left kidney into the general circulation, changes might have been detected in the right kidney. However, since neither of the agents delivered to the left kidney resulted in significant P∞ or conductance changes in the right kidney, we conclude the agents were delivered selectively and that only minimal quantities were passed from the renal vein into the systemic circulation. This same surgical approach could therefore be used to study the renal hemodynamic effects of other pharmacologic agents. | |
Limitations |
|
| A major drawback of the methodology used to apply the reservoir-wave approach to the renal circulation is that it is surgically intensive. Anesthesia and the extensive surgical preparation might have affected the results but such extensive measurements were not feasible in unanesthetized animals. Since we did not denervate the renal arteries, there could have been some influence of reno-renal reflexes, whereby interventions to one kidney could have resulted in functional changes by the contra-lateral kidney mediated via the sympathetic nervous system [31]. Renal nerves allow for two-way communication between the central nervous system and the kidneys which allows for the sympathetic regulation of renal blood flow, renin release and sodium and water balance [31]. Since our focus was on the application of the reservoir-wave approach to the renal circulation, we only examined the short-term alterations in vascular conductance, renal vascular resistance and P∞. A less invasive method of determining renal arterial pressure and flow would be required to determine any long-term hemodynamic consequences of increased renal ANG II and ET-1. | |
| Initially, the experimental protocol was particularly intensive surgically. In attempts to reduce the surgical stress, we abbreviated and simplified the protocol twice. (The methodology for measuring renal arterial pressure and flow and IVC pressure remained constant throughout all the experiments.) Most importantly, the results after the final iteration of the protocol confirmed the observations with respect to the breakdown of series resistance components that had been made with the initial protocol. | |
Conclusion |
|
| In this pilot study we applied the reservoir-wave approach to the renal circulation and the results suggest that the infusion of vasoconstrictors, either ANG II or ET-1, decreased the conductances of the infused kidney and that these decreases in conductance were due to increased P∞ and, therefore, increased microcirculatory/ venous resistance. | |
Acknowledgments |
|
| The study was supported by the inaugural The Kidney Foundation of Canada/Pfizer Canada -Cardio-renal Research Award. Also, the authors thank Cheryl Meek whose outstanding surgical expertise made these studies possible. | |
References |
|
|
|
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi