Research Article, Res J Opt Photonics Vol: 2 Issue: 1

Closed Form Wave Solution of Nonlinear Equations by Modified Simple Equation Method

Hossain AKMKS^1*, Akbar MA², Hossain MJ³ and Rahman MM⁴

¹Department of Mathematics, Begum Rokeya University, Rangpur, Bangladesh

²Department of Applied Mathematics, University of Rajshahi, Rajshahi, Bangladesh

³Department of Mathematics, University of Rajshahi, Rajshahi, Bangladesh

*Corresponding Author : Hossain AKMKS
Department of Mathematics, Begum Rokeya University, Rangpur, Bangladesh
Tel: 1911764291
E-mail: kazi_bru@yahoo.com

Received: November 20, 2017 Accepted: January 04, 2018 Published: January 09, 2018

Citation: Hossain AKMKS, Akbar MA, Hossain MJ, Rahman MM (2018) Closed Form Wave Solution of Nonlinear Equations by Modified Simple Equation Method. Res J Opt Photonics 2:1.

Abstract

Keywords: Modified simple equation (MSE) method; Third extended fifth order nonlinear equation; The nonlinear telegraph equation; nonlinear evolution equations (NLEEs); Closed form wave solutions

Mathematics Subject Classifications (2010)

35C07, 35C08, 35C09, 35K05, 35P99

Introduction

The study of the nonlinear evolution equations (NLEEs) and its closed form wave solutions has become very significant task in the recent years. The exploration of closed form wave solution is one of the easiest way to explains the evolution of the nonlinear wave phenomena that arises in the field of physical science and engineering. To better understand the inner mechanism of physical complex phenomena in nature, described by NLEEs, closed form wave solutions of NLEEs are essentially needed. In particular, the soliton solutions are very significant in the study of the models arising from various natural phenomena in scientific engineering fields such as optical fibers, high energy physics, nuclear physics, meteorology, geochemistry, elastic media, solid state physics, biophysics etc. Mathematical modeling of physical and engineering problems are inherently governed by nonlinear evolution equation (NLEEs). Therefore searching closed form wave solution of nonlinear evolution equations now becomes very important and interesting subject in nonlinear sciences. As a result, many authors who are concerned in nonlinear phenomena which exist in all fields of engineering and scientific works have been investigating the closed form wave solutions of nonlinear evolution equations. In recent times there are significant development have been made for exploring the closed form wave solutions of NLEEs and established many efficient and potential methods to solve the NLEEs for example the nonlinear transformation method [1], the sine-cosine method [2], the Exp-function method [3-6], the modified Exp-function [7], the Hirota’s bilinear transformation method [8,9], the variational method [10,11], the functional variable method [12], the modified simple equation method [13-18], the Adomian decomposition method [19], the extended direct algebraic method [20,21], the exp(- φ(η)) expansion method [22,23], the (G’/G) expansion method [24-30], the enhanced (G’/G) expansion method [31], the simplest equation method [32], the auxiliary ordinary differential equation method [33], the improve (G’/G) expansion method [34,35], the generalized Kudryashov method [36] etc. The recently developed modified simple equation method is getting attractiveness in use because of its straight forward and easy calculation procedure.

The aim of this paper to construct more closed form wave solutions of the nonlinear telegraph equation and the third extended fifth order nonlinear equation using the modified simple equation method. The remaining part of the paper is arranged as follows: In Section 2, method is described. In Section 3, the MSE method is applied to explore the solutions. In Section 4, graphical representation of the obtained solutions and In Section 5 conclusions are provided.

Description of Modified Simple Equation (MSE) Method

To describe the modified simple equation method we consider a nonlinear equation of two variables of x and t in the following form:

(1)

where P is polynomial of u(x, t) and its partial derivatives and u(x,t) is an unknown function.

The essential parts of this method are given in the following

Step 1: Introducing a compound variable ξ with the combination of real variables x and (2)

where c is the wave speed.

Equation (1) converts into an ODE with the help of Equation (2) of the following form:

(3)

where Q is a polynomial in u(ξ) and its derivatives with respect to ξ.

Step 2: The solution of (3) can be expressed of the form:

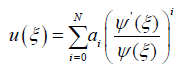(4)

Where ψ(ξ) is not known and to be calculated such that ψ’(ξ)≠ 0 and α_i(i=0,1,2,3,…N) are arbitrary constants to be determined such that α_N ≠ 0. Since ψ(ξ) is not known function or not a solution of any equation so it is not possible to guess in advance what kind of solution may be obtained. This is the exceptionality of this method. Therefore it might be possible to achieve some fresh solution by this method.

Step 3: The positive integer N can be evaluated by balancing the highest order of derivative term and nonlinear terms appearing in (3).

Step 4: Calculate the derivatives u’,u”,...and place in Equation (4) into (3) then we find the function ψ(ξ). These make a polynomial of (1/ψ(ξ)) and now equating the like terms of this polynomial to zero gives a system of algebraic and differential equation which on solving we get the values of αi ’s and ψ(ξ)'

Exploration of the Solutions

In this section, the modified simple equation method (MSE) has been put to use to examine the closed form solutions leading to solitary wave solutions to the third extended fifth order nonlinear equation and the nonlinear telegraph equation.

Example 1

Now we will apply the method which is described in section 2 to explore the closed form wave solution of nonlinear telegraph equation [36]:

(5)

Equation (5) is referred to as (1+1) dimensional hyperbolic telegraph equation with constant coefficients which models a mixture between diffusion and wave propagation by introducing a term that accounts for effects of finite velocity to standard heat or mass transport equation.

The wave transformation u(x,t)=u(ξ),ξ=x-ωt reduces the PDE (5) to ODE in the following form

(6)

where ω is a constant (wave speed) to be determined latter.

Balancing between the highest order derivative term u’’and highest order nonlinear term u³ gives n = 1.

Hence the solution form of (6) turns into

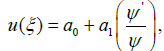(7)

Where α₀ and α₁ are constant such that α_i ≠ 0 and the unknown function ψ(ξ) to be calculated. Putting the value of (7) with its derivatives in equation (6) and equating the coefficient of ψ⁰, ψ^-1, ψ^-2, ψ^-3 to zero we attain the following successive algebraic and differential equation,

(8)

(9)

(10)

(11)

By Equation 8 and (11) we achieve and , since α_i ≠ 0. From Equation 10 it can be figure out that

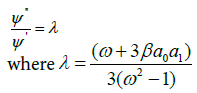(12)

Integrating Equation (12) with respect to ξ, yields

(13)

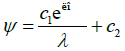and (14)

where c₁ and c₁ are arbitrary constants.

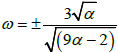Case 1: When and , solving equation (8) and (9) with (13) and (14), we achieve and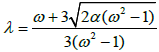 then substitute these values of α₀, α₁, ω and λ in (7) provides

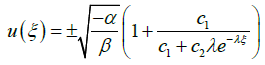(15)

Hence in u(x,t) variables, the general closed form wave solution of nonlinear telegraph equation is as follows:

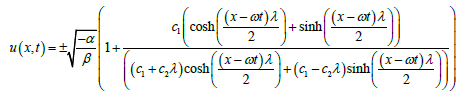(16)

As c₁ and c₂ are arbitrary constant one may randomly can choose their values. So if we let c₁ = 1 and c₂ = 1/λ then we get the following closed form wave solution

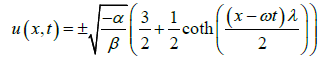(17)

Again setting c₁ = -1 and c₂ = 1/λ in Equation (16), we obtain the closed form wave solution of nonlinear telegraph equation of the form:

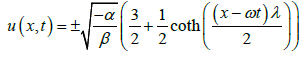(18)

Using hyperbolic functions identities, Equation (17) and Equation (18) can be rewritten as,

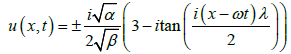(19)

and

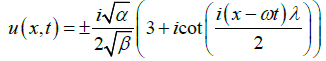(20)

where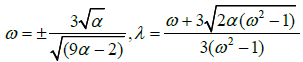

Case 2: When α_i = 0 and , solving equation (18) and (19) with (13) and (14), we get 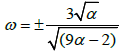and 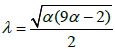then replace with these values of α₀, α₁, ω and λ in (17) provides the closed form wave solution in u(x,t) variables :

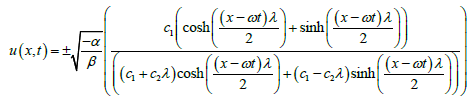(21)

Since c₁ and c₂ are arbitrary constant we may pick their values. If we replace c₁ = 1 and c₂ = 1/λ we get the closed form solution of nonlinear telegraph equation in the following form:

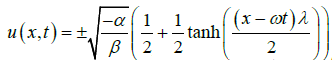(22)

Putting c₁ = -1 and c₂ = 1/λ in Equation (21) then the closed form wave solution is as follows

with hyperbolic functions characteristics, Equation (22) and Equation (23) can be modified as,

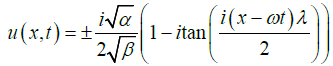(24)

and

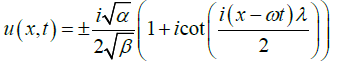(25)

Where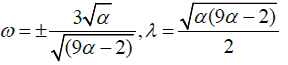

Example 2

In this subsection we will use the modified simple equation method to search the closed form wave solution of the third extended fifth order nonlinear equation of the form [37]

(26)

The wave transformation u(x,t)=u(ξ),ξ = kx+ly-ωt transfers (26) to the ODE of the form

(27)

Integrating (27) twice with respect to ξ and assuming the constant of integration to zero, we obtain

(28)

Balancing between the highest-order derivative term u’’’ and the highest-order nonlinear term u’² we get n=1.

Therefore, the solution of Equation (28) becomes

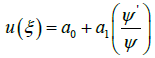(29)

Where ψ(ξ) is an unknown function to evaluated latter and α0 and α1 are constant such that α_i ≠ 0. Substituting Equation 29 with its derivatives into (29) and then equating the coefficient of ψ⁰, ψ^-1, ψ^-2, ψ^-3 to zero we get a system of successive algebraic and differential equation.

(30)

(31)

(32)

(33)

From Equation (33), we obtain α_i =3l.

And from Equation (30), we get

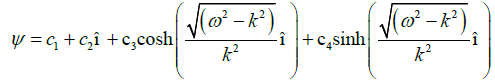(34)

Where c₁, c₂, c₃ and c₄ are arbitrary constants.

Solving Equation (31) by using (34) and α_i =3l we achieve ω = ±k.

Case 1: When αi =3l and ω = k then c₁ = c₁+ c₃

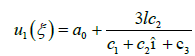(35)

Since c₁ and c₃ are constant so any one can put c₁ = c₁+ c₃. The general closed form wave solution of third extended fifth order nonlinear equation is as follows:

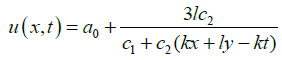(36)

where ξ = kx+ly- ωt and ω = k.

Case 2: When α_i =3l and ω = -k then

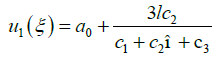(37)

Since c₁ and c₃ are integration constants, one may arbitrarily choose c₁ = c₁+c₃.Thus, the general closed form traveling wave solution of the third extended fifth order non-linear equation is obtained as follows:

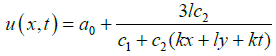(38)

where ξ = kx+ly- ωt and ω = -k

Graphical Representation of the Obtained Solutions

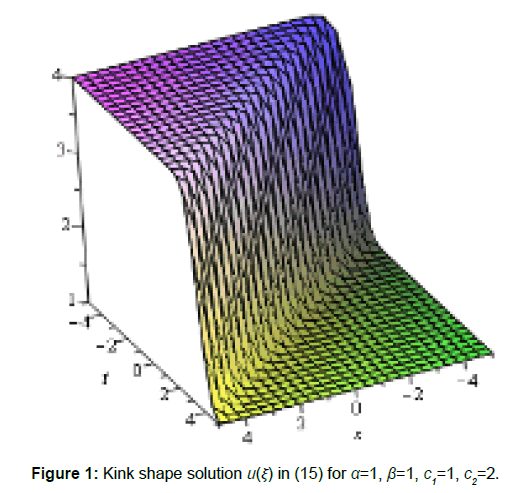
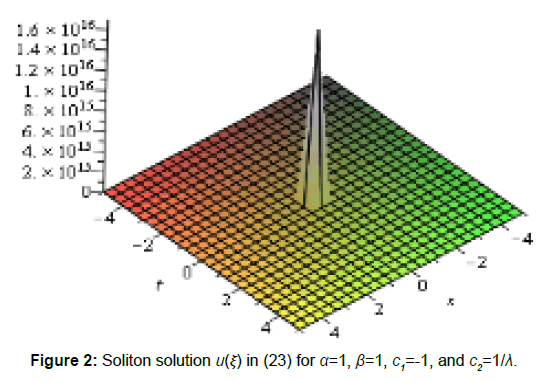
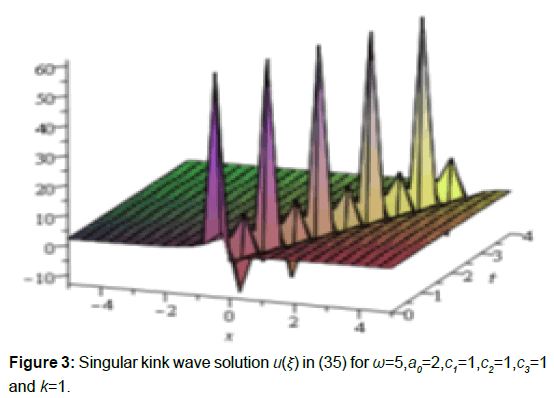
In this section, we have explained the obtained solutions of the nonlinear telegraph equation and the third extended fifth order nonlinear equation. From the above we observed that the solution from Equation 15, 17 and 19 travelling wave solutions which are kink shape type wave solutions. The solutions shown in Equation 18, 20, 23 correspond to soliton solution. The solution (Equation 15) is represented in Figure 1. Which express the nature of kink shape wave solution with α=1, β=1, c₁=1, c₂=2 and the interval -5≤ x,t ≤ 5.The soliton solution (23) for α=1, β=1, c₁=-1, and c₂=1/λ within the interval -5≤ x,t ≤ 5. is given by Figure 2. The figures of others solutions are similar to kink type and soliton type and ignored these figures for simplicity. Again the solutions of third extended fifth-order nonlinear equation we also observed that the solutions (35) to (38) are traveling wave solutions which are all Singular kink wave solution. The solution (35) is represented in Figure 3. It shows nature of singular kink shape travelling solution with wave speed ω=5, a₀=2, c₁=1, c₂=1,c₃=1 and k=1 with the interval -5≤ x ≤ 5 and 0 ≤ t ≤ 4. The figures of solution 36 to 38 are similar to singular kink type and ignored these figures for simplicity (Figure 3).

Conclusion

In this article, the modified simple equation method has been successfully applied to explore the closed form wave solution of two nonlinear equation named the nonlinear telegraph equation and the third extended fifth order nonlinear equation. The solutions are verified to test the correctness by putting the solutions back into the original equation and found correct. The used method has many advantages: it is straightforward and calculation procedure is very concise. Therefore this efficient method could be more effectively used to solve various NLEEs which regularly arise in science, engineering and other technical arenas.

Acknowledgements

The authors wish to take this chance to express their gratitude to the referees for their valuable observations and suggestions which improved the quality of this article.

References

1. Yang L, Liu J, Yang K (2001) Exact solutions of nonlinear PDE nonlinear transformation and reduction of nonlinear PDE to a quadrature. Phys Lett A 278: 267-270.
2. Wazwaz AM (2004) A applied sine-cosine method for handle nonlinear wave equations. Math Comput Modeling 40: 499-508.
3. Akbar MA, Ali NHM (2011) Exp-function method for duffing equation and new solutions of (2+1) dimensional dispersive long wave equations. Prog Appl Math 1: 30-42.
4. Naher H, Abdullah AF, Akbar MA (2011) The exp-function method for new exact solutions of the nonlinear partial differential equations. In J Phys Sci 6: 6706-6716.
5. Bekir A, Boz A (2008) Exact solutions for nonlinear evolution equations using exp-function method. Phys Letts A 372: 1619-1625.
6. Naher H, Abdullah AF, Akbar MA (2012) New traveling wave solutions of the higher dimensional nonlinear partial differential equation by the exp-function method. J Appl Math 1-14.
7. Hassan QMUl, Ahmad J, Shakeel M (2014) A novel analytical technique to obtain kink solutions for higher order nonlinear fractional evolution equations, abstract and applied analysis. Abstr Appl Anal 14: 1-11.
8. Hirota R (1973) Exact envelope soliton solutions of a nonlinear wave equation. J Math Phys 14: 805-810.
9. Hirota R, Satsuma J (1981) Soliton solutions of a coupled KDV equation. Phys Lett A 85: 404-408.
10. Helal MA, Seadawy AR (2009) Variational method for the derivative nonlinear schrodinger equation with computational applications. Physica Scripta 80: 350-360.
11. Seadawy AR (2011) New exact solutions for the KdV equation with higher order nonlinearity by using the variational method. Comp Math Appl 62: 3741-3755.
12. Cevikel AC, Beker A, Akar M, San S (2012) A procedure to construct exact solution of nonlinear evolution equations. Pramana J Phys 79: 337-344.
13. Akter J, Akbar MA (2015) Exact solutions to the benney-luke equation and the Phi-4 equations by using modified simple equation method. Results in Phys 5: 125-130.
14. Hossain AKMKS, Akbar MA, Wazwaz AM (2017) Closed form solutions of complex wave equations via modified simple equation method. Cogent Phys 4: 1312751.
15. Khan K, Akbar MA (2013) Exact and solitary wave solutions for the tzitzeica-dodd-bullough and the modified kdv-zakharov-kuznetsov equations using the modified simple equation method. Ain Shams Eng J 4: 903-909.
16. Hossain AKMKS, Akbar MA (2017) Traveling wave solutions of nonlinear evolution equations via modified simple equation method. Int Jour of App Math and Theoretical Phy 3: 20-25.
17. Khan K, Akbar MA, Ali NHM (2013) The Modified simple equation method for exact and solitary wave solutions of nonlinear evolution equation: the GZK-BBM equation and right-handed non-commutative burgers equations. ISRN Math Phys 1-5.
18. Hossain AKMKS, Akbar MA, Azad AK (2017) Closed form wave solutions of two nonlinear equations. Cogent Phys 4: 1-14
19. Adomian G (1994) Solving frontier problems of physics: the decomposition method. Springer Netherlands, Boston, MA.
20. Seadawy AR (2014) Stability analysis for zakharov-kuznetsov equation of weakly nonlinear ion-acoustic waves in a plasma. Comp and Math Appl 67:172-180.
21. Seadawy AR (2016) Three-dimensional nonlinear modified zakharov-kuznetsov equation of ion-acoustic waves in a magnetized plasma. Comp and Math Appl 71: 201-212.
22. Roshid HO, Alam MN, Akbar MA, Islam R (2015) Traveling wave solutions of the simplified mch equation via exp(-�?(x)) expansion method. British J of Math & Comp Sci 5: 595-605.
23. Islam R, Alam MN, Hossain AKMKS, Roshid HO (2013) Traveling wave solutions of nonlinear evolution equations via Exp(−Φ(η)) expansion method, Global J Sci Frontier Res 13: 63-71.
24. Naher H, Abdullah FA (2014) New approach of (G′/G) expansion method for rlw equation. Res J of App Sci Eng and Tech 7: 4864-4871.
25. Akbar MA, Ali NHM, Zayed EME (2012) Abundant exact traveling wave solutions of the generalized bretherton equation via (G′/G) expansion method. Commun Theor Phys 57: 173-178.
26. Akbar MA, Ali NHM, Mohyud DST (2012) The alternative (G′/G) expansion method with generalized riccati equation: application to fifth order (1+1)-dimensional caudrey-dodd-gibbon equation. Int J Phys Sci 7: 743-752.
27. Liu X, Tian L, Wu Y (2010) Application of the (G′/G) expansion method to two nonlinear evolution equations. Appl Math Comput 217: 1376-1384.
28. Alam MN, Akbar MA, Roshid HO (2013) Study of nonlinear evolution equations to construct traveling wave solutions via the new approach of generalized (G′/G) expansion method. Math Stat 1: 102-112.
29. Zhang ZY, Zhong J, Dou SS, Liu J, Peng D, et al. (2013) A new method to construct traveling wave solutions for the klein-gordon zakharov equations, Rom Journ Phys 587: 766-777.
30. Aslan I (2016) Exact solutions for fractional DDEs via auxiliary equation method coupled with the fractional complex transform. Math Meth Appl Sci 39: 5619-5625.
31. Hossain AKMKS, Akbar MA (2017) Closed form solutions of two nonlinear equations via enhanced (G′/G) expansion method. Cogent Math 4: 1312751.
32. Kudryashov NA (2005) Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Solitons Fractals 24: 1217-1231.
33. Zhang ZY (2013) Exact traveling wave solutions of the perturbed klein-gordon equation with quadratic nonlinearity in (1+1)-dimension, part i-without local inductance and dissipation effect. Turk J Phys 37: 259-267.
34. Naher H, Abdullah FA (2014) The improved (G′/G) expansion method to the (2+1)-dimensional breaking soliton equation. Journal of Computational Analysis & Applications 16: 220-235.
35. Zhang J, Jiang F, Zhao X (2010) An improved (G′/G) expansion method for solving nonlinear evolution equations. Int J Com Math 87: 1716-1725.
36. Zayed EME, Al-Nowehy AG (2016) Exact Traveling Wave Solutions for Nonlinear PDEs in Mathematical physics using the generalized kudryashov method. J Elec Eng 13: 203-227.
37. Wazwaz AM (2014) Kink solutions for three new fifth order nonlinear equations. App Math Modeling 38: 110-118.