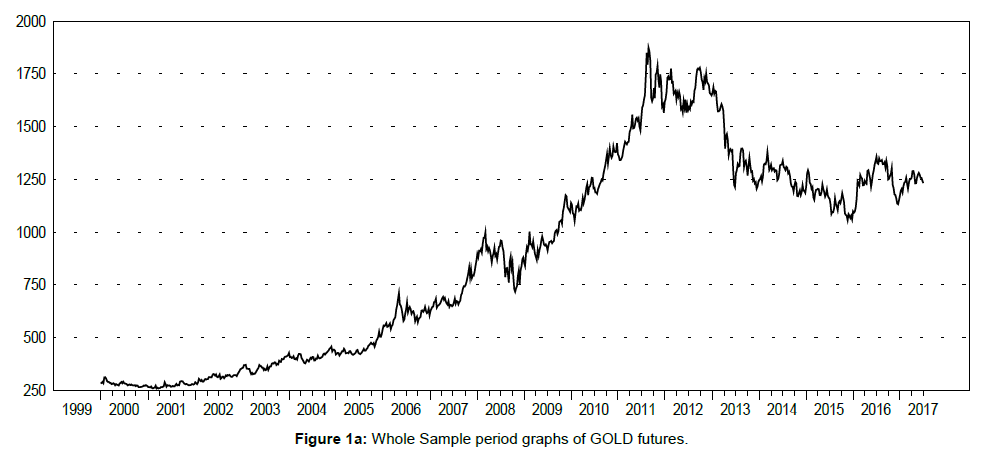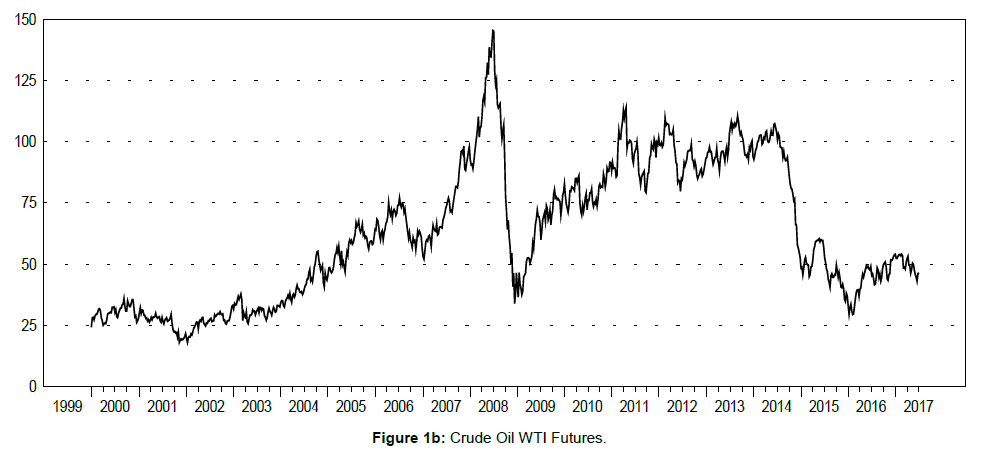Research Article, Res J Econ Vol: 1 Issue: 1
Crisis Effects on Relations between US Commodities Futures: An E-garch Approach
Dimitrios G Tsoutsas*
Department of Economics, University of Thessaly, Greece
*Corresponding Author : Dimitrios G Tsoutsas
Department of Economics, University of Thessaly, 78 Street, PC: 38333, Volos, Greece
Tel: 24210-74771/24210-74776
E-mail: dts@hotmail.gr
Received: September 16, 2017 Accepted: September 30, 2017 Published: October 06, 2017
Citation: Tsoutsas DG (2017) Crisis» Effects on Relations between US Commodities’ Futures: An E-garch Approach. Res J Econ 1:1.
Abstract
This paper estimates the nexus among gold futures, crude oil WTI futures, and natural gas futures before and after the global financial crisis’ outburst. Weekly data are employed and estimations are applied during two sub-periods by using a Nelson’s Exponential Generalized Autoregressive Conditional Heteroskedasticity (E-GARCH) approach in order to test for asymmetries in volatilities. Results provide evidence of significant effects of gold price on oil and gas price volatility in an exponential way, but reverse causality does not hold. Moreover, oil prices are found to depend on gas prices.
Keywords: Global financial crisis; Gold futures; Oil futures; Gas futures
Introduction
There is an increasing bulk of academic writing about effects of the global financial crisis on commodity prices in the US. The high volatility in financial markets that the domino effects of the Lehman Brothers collapse have brought about has been under scrutiny in a number of scientific studies. Our paper comes to fill a gap in the existing literature by employing an exponential GARCH approach to study inter-relations between three of the most important commodities traded in the US markets in times of extremely high volatility in the US economic conditions.
Batten and Lucey [1] examine volatility in the gold futures market by employing a GARCH methodology and find significant fluctuations across the trading day and week in volatility, which is related to information. Moreover, they argue that the price-sensitive information from other asset markets is consistent with the stochastic character of volatility in gold markets. Moreover, Tully and Lucey [2] by employing an asymmetric power GARCH model undertake an investigation of the gold price and find that it is in tight connection to the dollar. When it comes to Masih et al. [3], they argue that oil price fluctuations affect equity market performance in Korea. They also find that oil price shocks have a direct as well as an indirect effect on firm profitability. Interestingly, Suenaga et al. [4] examine the volatility dynamics of daily natural gas futures on the NYMEX and find strong seasonality due to a time-to-maturity impact. In another perspective, Pindyck [5] finds evidence of a statistically significant positive time trend in volatility for natural gas, whereas to a smaller extent for oil. Furthermore, he argues that crude oil volatility and returns have predictive power for natural gas volatility and returns, but the other way around does not hold.
Narayan et al. [6] by examining the long-run relationship between gold and oil futures prices at different maturities find that the oil market can be used for predicting the gold market prices as well as the other way around. Consequently, these two markets are found to be jointly inefficient. By another perspective, Hamilton and Wu [7] examine the use of futures contracts for hedging against commodity price risk and argue that significant alterations in oil futures risk premia have taken place since 2005 and risk premia on longer maturities have lowered. According to Alquist and Kilian [8], the negative sign of the oil futures spread could be regarded as an indicator of volatility in the crude oil quotes, which is driven by precautionary demand due to uncertainty.
To the best of my knowledge, this paper is the first to explore volatility inter-relations during the global financial crisis between US gold futures, oil futures, and gas futures by employing an E-GARCH methodology. The financial accelerator dynamics driven by ample liquidity provisions by the Federal Reserve through unconventional monetary practices should trigger inflationary pressures and spur commodities’ futures prices, which are considered as safer assets.
The remainder of this paper is structured as follows. Section 2 describes the data and methodology employed for econometric estimations. Section 3 provides and discusses the empirical results from the E-GARCH estimations. Finally, Section 4 concludes.
Data and Methodology
The data used are derived from the investing.com webpage and are in a weekly frequency. The variables employed are the gold futures quotes with a maturity of August 2017, symbolized as ‘‘Gold Futures - Aug 17 (GCQ7)’’, the crude oil futures of the same maturity, indicated as ‘‘Crude Oil WTI Futures - Aug 17 (CLQ7)’’, and the gas futures again of the same maturity, known as ‘‘Natural Gas Futures - Aug 17 (NGQ7)’’. The start date is January 3rd, 2000 and the end date is July 2nd, 2017. The estimation period is further divided into two sub periods, the first starting from January 3rd, 2000 and ending at September 30th, 2008. Notably, the second sub period starts on October 2008 where the after-Lehman Brothers collapse period onset took place and ends at July 2nd, 2017.
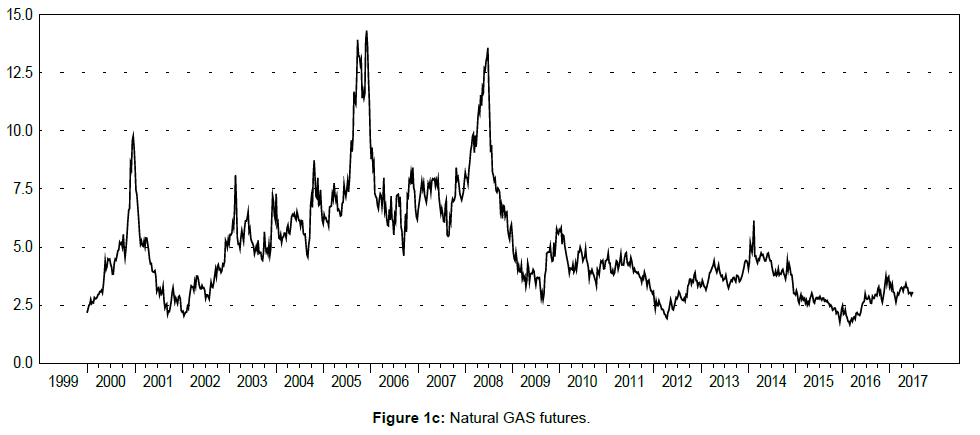
Figures 1a-c display the time curves of the futures quotes concerning each of the three commodities for the whole sample period. It is easily observed that the gold futures quotes present a significant upwards tendency which is most emphasized after the year 2005 up to 2012. Thereafter, a significant drop is detected during 2013, and the quotes are roughly stabilized from this time point up to the present. Moreover, the crude oil futures quotes are found to be severely increased from 2006 to 2008, whereas an even more intense fall is seen during 2008. This indicates that these derivatives were significantly influenced by the sudden outburst of the global financial crisis. Another sudden fall is obvious during 2014, while after that the crude oil futures quotes are stabilized. When it comes to the prices of natural gas futures, we observe a sudden increase during 2005, as well as another sudden rise of approximately the same magnitude just before 2008. Interestingly, after the sudden fall of these quotes during 2008, the natural gas futures prices were stabilized.
Moreover, Tables 1a-1c provides the descriptive statistics for each of these quotes series in the whole sample period, the pre-crisis sub period, and the post-Lehman Brothers collapse sub period. By being based on values of variance, we could argue that both of three series under consideration are highly volatile in the whole sample period, as well as in each of the sub periods. Furthermore, it should be emphasized that during the post-Lehman Brothers collapse sub period, there is a significantly higher level of kurtosis for all three futures commodities quotes. This is in tandem with the much higher mean values of gold and oil futures quotes for the same sub period. Nevertheless, it should be emphasized that higher values of positive asymmetry are present during the pre-crisis period, thereby strengthening the perspective that the crisis has negatively affected the US derivatives market. No great differences in terms of asymmetry are observable between sub periods.
| GOLD | OIL | GAS | |||
|---|---|---|---|---|---|
| Obs | 914 | Obs | 914 | Obs | 914 |
| Mean | 880.6353 | Mean | 62.26416 | Mean | 4.886303 |
| Std. Dev. | 469.8556 | Std. Dev. | 27.87455 | Std. Dev. | 2.270333 |
| Variance | 220764.2 | Variance | 776.9906 | Variance | 5.15441 |
| Skewness | .161429 | Skewness | .343418 | Skewness | 1.376416 |
| Kurtosis | 1.689567 | Kurtosis | 2.075839 | Kurtosis | 5.218644 |
Table 1a: Whole Sample Descriptive Statistics.
| GOLD | OIL | GAS | |||
|---|---|---|---|---|---|
| Obs | 457 | Obs | 457 | Obs | 457 |
| Mean | 464.4856 | Mean | 49.96602 | Mean | 6.154691 |
| Std. Dev. | 195.5126 | Std. Dev. | 26.99822 | Std. Dev. | 2.484514 |
| Variance | 38225.19 | Variance | 728.9039 | Variance | 6.172811 |
| Skewness | .9804895 | Skewness | 1.282105 | Skewness | .7701696 |
| Kurtosis | 2.889641 | Kurtosis | 4.244036 | Kurtosis | 3.765275 |
Table 1b: Pre-Crisis Descriptive Statistics.
| GOLD | OIL | GAS | |||
|---|---|---|---|---|---|
| Obs | 457 | Obs | 457 | Obs | 457 |
| Mean | 1296.785 | Mean | 74.5623 | Mean | 3.617915 |
| Std. Dev. | 238.0477 | Std. Dev. | 22.88295 | Std. Dev. | .9605408 |
| Variance | 56666.71 | Variance | 523.6294 | Variance | .9226387 |
| Skewness | .2348554 | Skewness | -.2294032 | Skewness | .5144593 |
| Kurtosis | 2.708069 | Kurtosis | 1.640782 | Kurtosis | 3.427155 |
Table 1c: Post-Crisis Outburst Descriptive Statistics.
The methodology applied is the Nelson Exponential GARCH approach Nelson [9], in order to examine whether there has been an exponential effect of the volatility of each commodity futures’ price on the corresponding price of another commodity’s futures. I select this approach as in my belief is the most suitable for examining alterations in quotes in times of large volatility and uncertainty in the derivatives markets of the US. As the Lehman Brothers collapse triggered a substantial destabilizing impact primarily in the US financial and capital markets, which was led by a high level of contagion, it is almost certain that effects were non-linear. Thereby, I employ an exponential structure in volatility studying so as to better capture non-linear dynamics. The interconnectedness and the level of substitutability among commodities are examined in a framework where the effect of each of the variables under consideration onto the others is under scrutiny. In order for better fit of results, all data are transformed into logarithmic differences before the estimations take place.
In the same vein with the original work of Nelson [9], let us assume that Zt is a series of independent identically distributed standardized random variables with mean 0 and variance 1. Notably, in an E-GARCH specification, volatility takes an exponential form and is modeled according to:
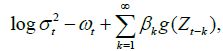
Where σ2 denotes variance, and ωt and βk are deterministic coefficients.
![]()
It can easily be derived that E[g(Zt)] =0
Notably, the conditional variance ![]() , being an explicit multiplicative function of lagged innovations, renders volatility capable of reacting asymmetrically to volatility-causing news. This is what differentiates the Exponential GARCH approach from the classical GARCH specification, as in the latter, the volatility is an additive function of the lagged error terms. Thereby, the asymmetrical character of the E-GARCH methodology enables the estimation of domino-fed and highly leverage-hit impacts of the Lehman Brothers collapse to be accomplished through in a highly more suitable theoretical and econometric framework.
, being an explicit multiplicative function of lagged innovations, renders volatility capable of reacting asymmetrically to volatility-causing news. This is what differentiates the Exponential GARCH approach from the classical GARCH specification, as in the latter, the volatility is an additive function of the lagged error terms. Thereby, the asymmetrical character of the E-GARCH methodology enables the estimation of domino-fed and highly leverage-hit impacts of the Lehman Brothers collapse to be accomplished through in a highly more suitable theoretical and econometric framework.
Empirical Results and Economic Implications
Empirical findings from E-GARCH estimations about the whole sample period, the pre-crisis period, as well as the period after the Lehman Brothers collapse, are presented in Tables 2a-2c, respectively. It should be highlighted that the main E-GARCH indicator, denoted as ‘‘egarch_a L1’’, represents exponential effects in lags of residuals estimated. Interestingly, in each sub period examined, this coefficient is found to be highly statistically significant providing credence to our choice of selecting this specification for estimating the global crisis effects. It should be noted that in the tables following, each variable’s effect is measured by the coefficient indicated by the respective variable, eg. ‘‘GOLD’’ or ‘‘OIL’’, whereas ‘‘earch_L1’’ stands for nonexponential lagged residuals, and ‘‘_cons’’ denotes a constant term.
| OIL | GAS | GOLD | GAS | GOLD | OIL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GOLD | .3418939 | GOLD | .2370913 | OIL | .1021114 | OIL | .3665044 | GAS | .0293547 | GAS | .1845069 |
| (0.000)*** | (0.014)** | (0.000)*** | (0.000)*** | (0.007)*** | (0.000)*** | ||||||
| earch L1. | .1023516 | earch L1. | .0967871 | earch L1. | -.00992 | earch L1. | .0855354 | earch L1. | -.0212464 | earch L1. | .1173514 |
| (0.000)*** | (0.015)** | 0.807 | (0.025)** | 0.595 | (0.000)*** | ||||||
| earch_a L1. | .3058657 | earch_a L1. | .2441685 | earch_a L1. | .4205492 | earch_a L1. | .3020629 | earch_a L1. | .4000857 | earch_a L1. | .334016 |
| (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | ||||||
| _cons | -5.998484 | _cons | -5.304281 | _cons | -7.46542 | _cons | -5.370938 | _cons | -7.422157 | _cons | -6.037264 |
| (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | ||||||
| Log-L | 1451.949 | Log-L | 1128.314 | Log-L | 2116.765 | Log-L | 1159.796 | Log-L | 2098.701 | Log-L | 1468.231 |
| Wald chi2(1) | 38.20 | Wald chi2(1) | 6.08 | Wald chi2(1) | 63.94 | Wald chi2(1) | 71.19 | Wald chi2(1) | 7.19 | Wald chi2(1) | 85.15 |
| Prob > chi2 | (0.000)*** | Prob > chi2 | (0.014)** | Prob > chi2 | (0.000)*** | Prob > chi2 | (0.000)*** | Prob > chi2 | (0.007)*** | Prob > chi2 | (0.000)*** |
Table 2a: E-GARCH estimations in the whole sample period, Impacts on each possible pair of derivatives of commodities are investigated.
| OIL | GAS | GOLD | GAS | GOLD | OIL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GOLD | .4482374 | GOLD | .5322146 | OIL | .0985416 | OIL | .5396598 | GAS | .0513847 | GAS | .2036987 |
| (0.000)*** | (0.001)*** | (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | ||||||
| earch L1. | -.0254224 | earch L1. | .0639368 | earch L1. | -.0085373 | earch L1. | .054057 | earch L1. | .0126467 | earch L1. | -.0371476 |
| 0.538 | 0.295 | 0.881 | 0.318 | 0.826 | 0.469 | ||||||
| earch_a L1. | .2517311 | earch_a L1. | .2201763 | earch_a L1. | .3608479 | earch_a L1. | .3439792 | earch_a L1. | .4379549 | earch_a L1. | .2323441 |
| (0.005)*** | (0.033)** | (0.000)*** | (0.000)*** | (0.000)*** | (0.002)*** | ||||||
| _cons | -6.060197 | _cons | -5.143986 | _cons | -7.4528 | _cons | -5.224543 | _cons | -7.440581 | _cons | -6.110076 |
| (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | ||||||
| Log-L | 737.5508 | Log-L | 526.9564 | Log-L | 1054.532 | Log-L | 547.6244 | Log-L | 1052.523 | Log-L | 748.5999 |
| Wald chi2(1) | 18.13 | Wald chi2(1) | 11.81 | Wald chi2(1) | 18.19 | Wald chi2(1) | 52.71 | Wald chi2(1) | 12.98 | Wald chi2(1) | 61.38 |
| Prob > chi2 | (0.000)*** | Prob > chi2 | (0.000)*** | Prob > chi2 | (0.000)*** | Prob > chi2 | (0.000)*** | Prob > chi2 | (0.000)*** | Prob > chi2 | (0.000)*** |
Table 2b: E-GARCH estimations in the sub period before the outburst of the crisis, Effects on each possible pair of derivatives on commodities are examined.
| OIL | GAS | GOLD | GAS | GOLD | OIL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GOLD | .225175 | GOLD | -.0072696 | OIL | .10419 | OIL | .2386106 | GAS | .0006741 | GAS | .1381861 |
| (0.001)*** | 0.950 | (0.000)*** | (0.000)*** | 0.969 | (0.000)*** | ||||||
| earch L1. | .2539735 | earch L1. | .1386403 | earch L1. | -.022956 | earch L1. | .1302503 | earch L1. | -.0664464 | earch L1. | .2438642 |
| (0.000)*** | (0.012)** | 0.719 | (0.021)** | 0.264 | (0.000)*** | ||||||
| earch_a L1. | .394196 | earch_a L1. | .2895454 | earch_a L1. | .5039422 | earch_a L1. | .3071596 | earch_a L1. | .401762 | earch_a L1. | .418011 |
| (0.000)*** | (0.006)*** | (0.000)*** | (0.003)*** | (0.000)*** | (0.000)*** | ||||||
| _cons | -5.938898 | _cons | -5.515687 | _cons | -7.477113 | _cons | -5.56282 | _cons | -7.422074 | _cons | -5.967646 |
| (0.000)*** | 0.000 | (0.000)*** | (0.000)*** | (0.000)*** | (0.000)*** | ||||||
| Log-L | 719.584 | Log-L | 613.2219 | Log-L | 1062.632 | Log-L | 623.6334 | Log-L | 1050.303 | Log-L | 724.6752 |
| Wald chi2(1) | 10.22 | Wald chi2(1) | 0.01 | Wald chi2(1) | 46.78 | Wald chi2(1) | 21.56 | Wald chi2(1) | 0.01 | Wald chi2(1) | 20.66 |
| Prob > chi2 | (0.001)*** | Prob > chi2 | 0.9502 | Prob > chi2 | (0.000)*** | Prob > chi2 | (0.000)*** | Prob > chi2 | 0.9687 | Prob > chi2 | (0.000)*** |
Table 2c: E-GARCH estimations in the sub period after the outburst of the financial crisis, Impacts on each possible pair of derivatives of commodities are under scrutiny.
Results for the full sample period provide evidence that gold futures’ prices indeed affect oil futures’ prices as well as gas futures’ prices in a positive manner, as they are increased by 0.34 and 0.24, respectively. Moreover, the exponential impacts of gold futures’ prices on oil futures’ prices and gas futures’ prices are also found to be positive and statistically significant. Notably, all exponential effects are found to be positive (0.3058657, 0.2441685, 0.4205492, 0.3020629, 0.4000857, 0.334016) and statistically significant at the 1% level (each p-value is equal to 0.000). Interestingly, these basic commodities futures’ quotes seem to move towards the same direction, indicating that higher gold hedge prices lead to higher oil hedge prices and higher gas hedge prices in an exponentially increasing manner. All results are characterized by high levels of robustness (as p-values of each coefficient as well as the Prob statistic indicate by being near zero). Nevertheless, the other directions of causality that are effects from oil or gas futures quotes to gold futures quotes are not found to be statistically trustworthy. Notably enough, there is evidence that oil futures’ prices have a positive and statistically significant impact on gas futures’ prices in an exponential way and this is also valid the other way round.
Based on the econometric estimations concerning the first sub period (pre-Lehman Brothers collapse period), results are in high resemblance to the overall period case. Interestingly, the gold futures’ quotes are also found to be affected by the oil and gas futures’ quotes (0.0985416 and 0.0513847, respectively) but the exponential character of these impacts is not as strong as in the rest of the relations. Gold futures prices are found to be exponentially affected by gas futures prices in a stronger degree than affected by oil futures prices (0.3608479 and 0.2323441, respectively).
Outcomes from estimations about the after Lehman Brothers default period provide similar evidence to the pre-crisis sub period. The exponential impacts are found to be positive (0.394196, 0.2895454, 0.50394422, 0.3071596, 0.401762, and 0.418011) and statistically significant, as all p-values tend to zero (0.000, 0.006, 0.000, 0.003, 0.000, and 0.000). It is noteworthy that the impacts of gold futures’ quotes on oil futures’ quotes and gas futures’ quotes become weaker. When the reverse causality is examined, gas prices are found to affect gold prices in an exponentially negative manner. The same is found for gas quotes’ effects on gold quotes, where the negative exponential impact is higher than before, but remains statistically non-significant.
Conclusion
This study examines how US gold, oil, and gas futures quotes affect each other’s volatility in prices during the high uncertainty period of the global financial crisis. There is evidence derived from E-GARCH econometric estimations that gold futures prices affect oil futures prices in a modest extent, as well as gas oil prices in a lesser extent. Interestingly, the reverse effect does not hold in a statistically significant manner. Moreover, oil futures quotes and gas futures quotes are found to affect each other by bringing about higher volatility levels from one to the other, in an exponentially asymmetric way.
Notably, effects of commodities futures quotes become less positive and weaker during the crisis perhaps owing to the increased uncertainty and volatility due to external factors that prevail during the crisis. A tendency towards negative signs of effects of futures quotes between commodities is found by estimations.
As the main consequence of the global financial crisis has been the emergence of high volatility in financial markets, the aim of this paper is to cast light on volatility dynamics during unconventional eras. This way, we fill a gap in the recent literature about commodities interrelations during non-ordinary economic conditions. Effects of the Lehman Brothers collapse on the US real economy have to be studied through its impact on asset prices, mainly via the quotes of financial derivatives, due to the highly sophisticated character of US financial markets. The fluctuations of derivatives on basic commodities that stand out as main drivers and re-presenters of economic growth provide a more granular look on the US economy perspectives. Moreover, they effectively capture heterogeneity in price reactions and measure the financial but also consequently macroeconomic instability that domino effects bring about, in a nutshell. One of the main motivations in writing this paper is helping even by the slightest degree in the research towards this direction.
References
- Alquist R, Kilian L (2010) What do we learn from the price of crude oil futures? J Appl Econ 25: 539-573.
- Batten JA, Lucey BM (2010) Volatility in the gold futures market. Appl Econ Lett 17: 187-190.
- Hamilton JD, Wu JC (2014) Risk premia in crude oil futures prices. J Int Money Finance 42: 9-37.
- Masih R, Peters S, De Mello L (2011) Oil price volatility and stock price fluctuations in an emerging market: evidence from South Korea. Energy Econ 33: 975-986.
- Narayan PK, Narayan S, Zheng X (2010) Gold and oil futures markets: Are markets efficient? Appl Energy 87: 3299-3303.
- Nelson DB (1991) Conditional heteroskedasticity in asset returns: A new approach. Econometrica 1: 347-370.
- Pindyck RS (2004) Volatility in natural gas and oil markets. The Journal of Energy and Development 30: 1-9.
- Suenaga H, Smith A, Williams J (2008) Volatility dynamics of NYMEX natural gas futures prices. Journal of Futures Markets 28: 438-463.
- Tully E, Lucey BM (2007) A power GARCH examination of the gold market. RIBAF 21: 316-325.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi