Research Article, J Polym Sci Appl Vol: 6 Issue: 1

Dissipative Particle Dynamics Simulation of Free and Restricted Polymer Chain Motion under External Force in Nano-Channel

Ramin Zakeri^*

Department of Mechanical Engineering, Shahrood University of Technology, Shahrood, Iran

*Corresponding Author: Ramin Zakeri
Department of Mechanical Engineering, Shahrood University of Technology, Shahrood, Iran
E-mail: r_zakeri@shahroodut.ac.ir

Received date:  07 December, 2021, Manuscript No. JPSA-21-28393;

Editor assigned date: 09 December, 2021, PreQC No. JPSA-21-28393 (PQ);

Reviewed date: 23 December, 2021, QC No JPSA-21-28393;

Revised date: 03 January, 2022, Manuscript No. JPSA-21-28393 (R);

Published: 07 January, 2022, DOI:10.4172/jpsa.1000119

Citation: Zakeri R (2022) Dissipative Particle Dynamics Simulation of Free and Restricted Polymer Chain Motion under External Force in Nano-Channel. J Polym Sci Appl 6:1.

Keywords: Dissipative Particles Dynamics (DPD); Micro/Nano flow; Polymer chain; Numerical simulation

Introduction

From biology and medicine to space exploration, the subject of micro/nanofluid transfer along with solid nanoparticles or polymer nanofibers has always been important. For example, biological samples are usually transported by microfluidics, and this is done by micro-systems, or by cooling through a heat exchanger and using nanofluids. It seems that the topic of nano/microfluid, which is used for biological sample transfer or solid particle transfer, is a very practical and important issue in the fine scales [1-7].

From a practical point of view, the transfer of fluid with particles is done by micro pumps, such as drug delivery to patients [8] or cooling of electronic components by nanofluid transfer [9]. The proposed fluid transfer methods are very diverse, such as electrosmotic micropumps [10]. Interaction of Electric field motion and electrostatic surface, magnetic hydrodynamics (magnetic field motion and Lorentz force), piezoelectric (electric field vibrations), acoustic (wave pressure gas increase) and Also, one of the common practical and simple methods of particle fluid transfer by micro-pressure gradient pump is that in this research, the last method has been selected. In this method, by creating a constant pressure gradient, all fluid particles begin to move under the influence of a constant force [11-14].

Also, the transfer of polymer by microfluid and micropump has been studied by researchers to investigate various applications such as polymer chain transfer, DNA, separation and different species and blood cells. One case in point is the study of the behavior of polymer chains or their complex behavior in nano/microfluids. The study and analysis of polymer chain movement in various fields of study such as biology, genetics, etc. is very essential. Transfer of polymers by micro/nanofluid is observed in many biological processes in living cells or chemical processes through narrow pores, protein transfer through cell membranes and the penetration of viruses into the cell nucleus. Knowledge of the behavior and motion of the polymer chain is very useful in the design and fabrication of transmitter microsystems as well as the behavior of the biosystem or drug delivery [15].

The difficulties and costs associated with experimental studies have led researchers to use computational simulation methods as a primary design and analysis tool that is very useful for designing and understanding the complex behavior of polymer chains [16]. The most important and classic method of simulation is the molecular dynamics method. This method is used in very small nanometer scale and is not suitable for simulation of many application microsystems because it has very high computational costs, although simulation with this method is very close to real physics. To overcome this limitation, researchers have sought methods that are less computationally costly but at the same time closer to the actual physics of non-continuous and molecular fluids [17]. The latest method proposed is the Dissipative Particle Dynamics (DPD) method. The DPD method is a mesoscopic method that has been widely used in micro/nanoscale simulations recently. In this method, using molecular clusters, known as particles, instead of considering all real molecules, all the motion and collision of clusters or particles are considered as a group and has a lower computational cost compared to the molecular dynamics method [18,19].

The most recent proposed method, the Dissipative Particle Dynamics (DPD) method [20], used the DPD method to study the dynamics and rheology of polymer solutions and suspensions consisting of spherical particles with adsorbed polymers. They found that both polymer solutions and polymer domain suspensions have Newtonian behavior with low shear rates, while they perform thin shear behavior for higher shear rates [21] used the DPD method to study the behavior of a polymer within a capillary and the effect of polymers on the melting process in a shear flow. Based on the DPD method proposed an electrophoresis model for DNA that was able to simulate the electroosmotic and electrophoretic motion of the accompanying DNA in the micro/nanoscale channel [22].

Using this model, they were able to obtain free-moving DNA discharge while avoiding expensive electrostatic interactions in molecular simulations. They also calculated the movements of the particles in realistic geometry with great precision [23]. Used the DPD method to study the separation of diets in a micro device using the entropic trapping mechanism. They showed that longer strands of DNA were faster than shorter strands. They concluded that entropic trapping was the result of delayed entry. In addition, they concluded that trapping the particles in a corner did not help to isolate the DNA [24]. Studied the effect of Schmidt number on the rheology of nonlinear elastic chains using the DPD method studied single and bilayer layers of polymer coatings using DPD method [23]. They focused on possible differences between the link ring and the linear polymer chains in relation to the radius of rotation, roughness, orientation, and density profiles as functions of distance from the link plate. They also studied the laws of the gyration radius and normal and parallel components used the DPD method to simulate the performance of a soft polymer micro-stimulator in an electrosmotic flow in a simple micro-channel and a divergent convergent. The results showed that the displacement of soft polymer increases with increasing electric field, number of grains and decreasing harmonic bond coefficient [25].

In this study, considering that the movement of the chain in free mode (free polymer chain) and restricted conditions (two fixed ends of a polymer chain), comparison between two cases has been carried out for finding more about flow behavior on polymer chain including investigation of polymer displacement, gyration radius, velocity auto correlation function. All of the study has been followed with assumption of constant external force in DPD formulation. Numerical simulation of Dissipated Particle Dynamics (DPD), polymer chain and the present model as mentioned, the molecular dynamics method considers each particle as a molecule and the collision between particles is according to Newton's second law. The temporal and longitudinal scales of this method are very small and if we want to use it in larger scale (mesoscale), it will have a high computational cost. In the particle dynamics method, the number of molecules is considered as a particle. The mesoscopic method is a coarse-grained method in which each particle with mass of m_i represents a large number of molecules. The relationship between velocity (v→_i), position (r→_i), and force between particles, like the molecular dynamics method, is written according to the relationship of Newton's second law, which is presented below [26].

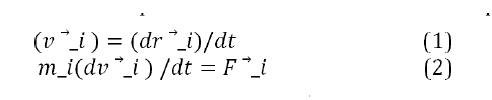
In general, the force F→_i consists of two general external and internal forces. The external force is the same as the magnetic or electrosmotic force, and the internal force is the intermolecular force, which includes the three survival forces, the random f→_ij^R and the dissipation f →_ij^D, which are listed below [26].

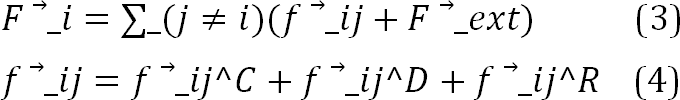
Note that the two forces of dissipation and random are entered into the calculations because this method, unlike the method of molecular dynamics, examines the collision of the representatives of molecules and the creation of two forces of dissipation and randomness based on the mathematics of cluster collision is mandatory. It should also be noted that if a pressure difference or a constant force is considered, which is considered in this article, the external force is considered a fixed value. This term is the same as the source term in the CFD which is used to account for external force. Conservative force is derived from the internal force classification of Leonard Jens's mediation, which is defined as follows [27].

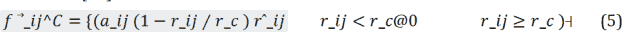
In the above relation a_ijis the collision coefficient of two particles i and j and outside the collision radius is considered zero. Also, based on the DPD formulation r_ij=|r→_ij |, r Ì?_ij=r→_ij⁄|r→_ij | and aij=75kBT/ρ Also, the other two terms of the internal forces of dissipative force and random force are calculated by relations (10), respectively:

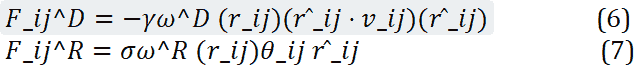
θi is a random function with zero mean properties and a single variance. In the above equations σ and γ, respectively, the power factor for acceleration and random forces vij = (vi- vj), and ωD and ωR are two weight functions, which are calculated in the following equation.

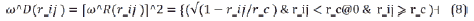
The Verlet algorithm is used to solve the above equations. According to this algorithm, with the initial assumption of velocity values, the displacement is initially calculated and then the forces between particles are calculated and in the iteration loop a new velocity and a new position are calculated and the force field is updated and the velocity and position values of the particles are updated again. As mentioned, the polymer chain consists of a number of beads and springs between them. To simulate the presence of a polymer chain in the flow, the force calculation field includes particle-to-particle collision, particle to polymer beads collision, and polymer bead to polymer bead collision, which must be taken into account in the calculation of survival force. In other words, particle collisions include bead-to-bead collisions with bead to fluid particles. Also, between the items in this type of spring simulation, it is assumed that it is necessary to calculate the spring force and add it to the survival force. Due to the collision of fluid particles or spherical particles with each other, they cause the spherical particles to move relative to each other and the spring force is increased [28,29].

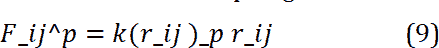
In the above relation k (r_ij )_p is the hardness coefficient which is considered the same for all items in the present simulation. In the force field calculation loop, the spring force between the beads is calculated and added to the conservative force at the moment the DPD grains hit the beads or bead to bead, and the force field is updated [30]. The model in this research is a polymer chain within a simple channel in the nanochannel that moves under the constant force of nanofluid particles and causes a change in the state of the polymer chain, which is like connecting a number of beads and springs to each other. The walls of the channel are made of solid particles and are returned to the field of motion when the fluid particles collide. Determination of fluid material, walls and polymer chain beads was explained numerically. As the particles leave the channel, a periodic boundary condition causes the particles to return to the computational field at the beginning of the channel. Figure 1 shows the introduced model, which in the next section; the results of polymer movement in the channel will be reviewed and analyzed. To develop our result for finding more about polymer chain behavior in free and restricted modes, the radius of gyration and the Velocity Auto-Correlation Function (VACF) would be so effective. The radius of gyration formulation is

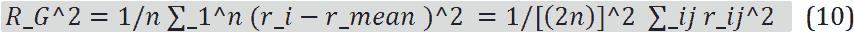
In which n is the beads number in a monomer, r_ mean is the mean position of the polymer chain and r_ij=|r→_i-r→_j |. Also, formulation of VACF is at the first, should be calculated [30].

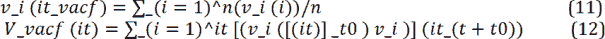
Where (v_i) velocity of the center-of-mass of the polymer chain it_vacf is iteration number of time step, (((it))_t0) and (it_(t+t0) ) are the initial time of polymer motion and summation of initial time with delay time [31].

Results

In this section, we examine the results obtained from the DPD simulation of the displacement of polymer beads in two modes of free movement and a polymer with two fixed ends which is assumed that the motion factor is under the influence of constant force. First, the results for a simple channel are compared with the analytical results, and then the above cases are investigated to investigate the complex behavior of the polymer chain in the two cases.

3-1-Validation of DPD particles in nano channels

As mentioned, the new method of dissipating particle dynamics is a reliable method for simulating non-continuous fluids in multi-nanometer-to-micro scales. This method has the advantage of having a larger time and length scale compared to molecular dynamics method and the same as the lattice Boltzmann method [11] (reducing the computational cost) while by increasing the number of degrees of freedom (advantage over the lattice Boltzmann method) will give more realistic simulation than the LBM or CFD method. The geometry in this study consists of a simple channel in which DPD particles are placed and the walls are made of particles and the bounce back condition is applied. The particles are also directed to the beginning of the channel by implementation of periodic boundary condition when they reach the end of the channel. The particle motion is a constant external force that causes the particles to be pushed forward and reach its maximum velocity in the zero velocity walls and in the half channel.

In Table 1, the simulation condition in a simple channel under the influence of the constant force of the pressure gradient is given and in figure 2, the velocity profile diagram in the fully developed state is compared by DPD method and analytical solution. As the particles move by a constant force, the particles that are close to the wall are more affected by the shear force and have a lower velocity, while as the distance from the wall increases, the shear force decreases and the velocity of the particles increases. Note that the non-continuous motion of particles and the collision of particles always fluctuate in the actual physics of flow. The accuracy of the results shows that less than 10% of the difference between the results and the analytical results is reported. As mentioned, this percentage of difference is due to such fluctuations in particle motion that it is inherent in the Lagrangian solution method and is closer to the real physics of particle motion.

Table 1: Constant value for simulation of nanofluid motion in the nanochannel.

Figure 1: Schematic of DPD particle motion in a channel. (A) Free motion, (B) Resisted motion.

Schematic of DPD particle motion in a channel with periodic and bounce-back boundary condition and presence of polymer chain in nanochannel for two cases of free motion (A); and resisted motion of polymer chain (B).

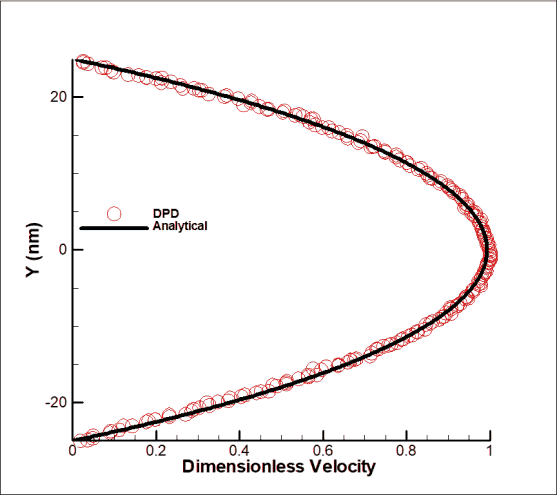
Figure 2: Comparison of DPD (circle) and analytical (continuous line) simulation solution of velocity profiles in simple channel for constant force mode (pressure difference).

3-2 Development of results in the free polymer chain motion condition

In this study, a polymer chain is placed in the channel away from the channel walls and the movement of the polymer under the influence of a constant forward force and the application of a periodic boundary condition in different states of elastic force between the beads is investigated. When particles hit the beads, considering the spring stiffness coefficient, it will cause the motion of polymer chain. Figure 3 shows the motion of a polymer with a hardness coefficient of 8000, a coefficient of collision of a polymer with a fluid of 18, and a polymer with a polymer of 10 over a period of 4.5 seconds. Over time, the polymer moves forward under the influence of DPD particles. There is no holding force to prevent the polymer chain from moving, and the polymer moves freely for a few nanometers in 4.5 seconds. How the polymer moves depends on the direction of the particles, the stiffness of the items. Based on Equation 5, we have several types of collisions, including the collision of fluid particles with each other, fluid to polymer, and polymer to polymer. The polymer is also affected by this collision field and shows a complex motion. The question here is that what the effect of changing the hardness coefficient (polymer type) is on the displacement rate which is answered as follows. To further investigate the issue, the stiffness ratio between the items has been changed to affect how it moves.

Figure 4 shows the different modes of motion of the polymer considering the hardness coefficients of 5000, 6000, 7000 and 8000. Note that two types of boundary conditions are used in this simulation, namely the bounce back boundary condition used in the channel wall and the periodic boundary condition in which particles are directed to the beginning of the channel when they reach the end of the channel. The polymer is brought to the beginning of the channel by reaching the end of the channel. As can be seen, with increasing the hardness of the polymer, not only does the polymer have less displacement but also it tends to stand vertically while in the case of lower hardness coefficient, the polymer has moved more freely to the sides. Overall, with a 1.6 time increase in hardness, a 53% reduction in polymer displacement was observed.

Then, to investigate the behavior of the polymer in 4.5 seconds, the two parameters of gyration radius and velocity correlation function are investigated in figure 5; the first shows the degree of turbulence of the polymer chain position over time and the second parameter shows the speed fluctuations of the polymer chain. As expected, as the stiffness coefficient increases, the gyration radius also decreases and the motion fluctuations of the polymer decrease over time. Also, the velocity correlation function shows velocity fluctuations in different stiffness coefficients that do not have a specific decreasing or increasing trend and only show velocity turbulence in all cases. The above study shows that with increasing the hardness coefficient of the polymer, it tends to stand against flow and less movement occur and will fluctuate less due to the hardening of the spring force. The important point is that by increasing the stiffness coefficient, the nonlinear behavior in displacement is observed, which is further investigated at the end of the study and compared with the two-way restrained motion (Figures 3-5).

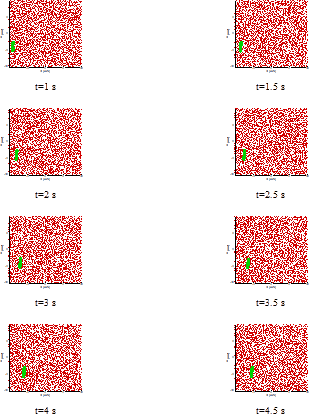
Figure 3: Free movement of the polymer chain in a simple channel under the influence of a constant external force of 0.01 and a hardness coefficient of 8000 between the spheres for a free polymer chain in 4.5 seconds.

Figure 4: Free movement of the polymer in a simple channel with different hardness coefficient and constant force 0.01.

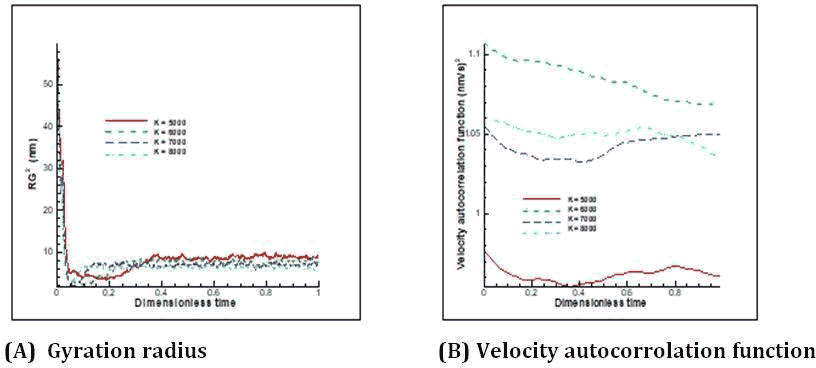
Figure 5: Changes in gyration radius (A) Velocity correlation function (B) Over time for free movement of the polymer chain in different stiffness (bond coefficient) states.

3-3 Development of results in the restricted polymer chain motion condition

Next, in order to develop the results, it is considered the two fixed ends of a polymer chain (first and last beads of polymer chain). Due to the movement of DPD particles by constant force, the interaction of fluid particles with polymer will cause to transfer the momentum and the polymer chain tends to stretch. It should be considered that because of restrictions of spring between beads and two fixed ends of a polymer, a restricted motion of polymer is formed over time steps. On the other hand, the collision of particles in different directions will be limited. In Figure 6, two fixed ends of a polymer are installed at points 4 and -4, in which the tendency to stretch appears under the influence of the constant force of the pressure gradient and the motion of the DPD particles. In the first second, the amount of elongation is very small, but with the movement of particles and collisions, and on the other hand, trapping of some particles and momentum transfer, the amount of elongation increases until it is almost completed in 1.5 seconds, after which the polymer maintains its position. For 50 beads, a hardness coefficient of 8000 and a constant force of 0.01 results in about 20% displacement is resulted in relative to the channel width.

One of the things we are looking for in this research is the effect of changing the hardness coefficient on the displacement rate of the polymer. By changing the hardness coefficient, the amount of polymer movement changes and is shown in Figure 7. In this study, by increasing the hardness coefficient by 1.6 times, the displacement rate decreased by 37% compared to the hardness factor of 5000. The displacement process is not completely linear due to the spring effect, but the displacement process is more linear than the free polymer displacement mode, which is further explained at the end of the section. In order to investigate the complex behavior of the polymer over time, two properties of the polymer chain motion have been studied, which are the gyration radius and the velocity autocorrelation function. By reducing the hardness coefficient, the polymer moves to the sides more easily, and in addition to more tension, the irregularity of movement also increases a little, and the radius of rotation moves with more turbulence. Also, the correlation function shows, as mentioned before, the velocity turbulence in motion, but does not show a specific decreasing or increasing trend such as the rotation radius, which is shown in Figure 8. This study, as in the previous case, shows that with increasing the hardness coefficient, the polymer displacement decreases and the tendency to maintain the initial state is higher and has a more linear trend than the first case. Figure 9 shows a comparison diagram of the displacement of the polymer chain in 4.5 seconds in different modes of stiffness in the two modes of free movement and motion with restraint mode with the assumption of constant force. As can be seen, although both modes show decreasing behavior in displacement with increasing stiffness coefficient, there is a uniform nonlinear behavioral pattern in the free motion mode. In the free motion mode, with increasing stiffness coefficient, the tendency to move with the collision of DPD particles decrease and there is a greater tendency to stand and without tendency to move, while in the restrained motion mode, a more linear motion is shown by changing the stiffness coefficient. In other words, by moving the particles and colliding with the two fixed ends of a polymer, the momentum is transferred more efficiently, and some particles are trapped in the chain, and the momentum transfer is performed better, and figures 9 shows higher linear displacement compared to free motion.

In general, by increasing the stiffness coefficient by 1.6 times, a 53% reduction in displacement has been calculated for the free movement mode and a 37% reduction in displacement for the two fixed ends of a polymer or restricted mode. Also, by calculating the standard deviation in the two cases of free and restricted motion for the parameters of the gyration function and the velocity correlation function in Figure 10, it is important to note that the trend of gyration radius changes as shown earlier and has a decreasing trend. In both cases, the chain motion decreases sharply with increasing stiffness, resulting in a smaller turning radius, which results in more decreasing changes in contrast to free movement. It is noteworthy that the velocity correlation function reports changes in oscillating velocity over time, which are reported by changes in the stiffness coefficient and turbulence of the polymer chain. The above study shows that the DPD method is a reliable and efficient method for predicting the complex behavior of polymer chains and can be used in various other cases (Figures 6-10).

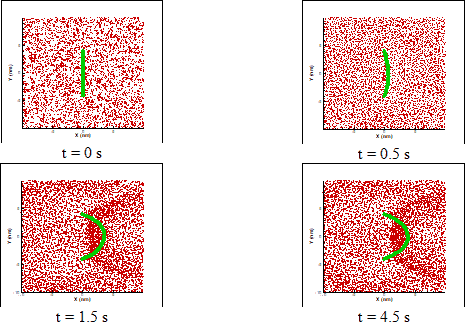
Figure 6: Movement with two fixed ends of a polymer chain in a simple channel under the influence of a constant external force of 0.01 and a stiffness coefficient of 8000 between the spheres.

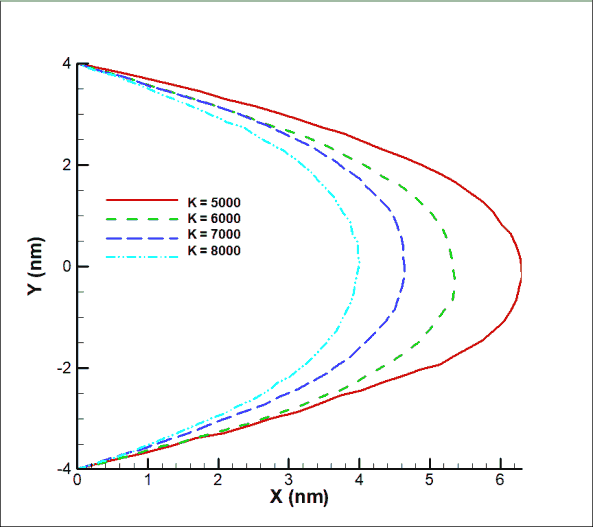
Figure 7: Movement with two fixed ends of a polymer chain in a simple channel considering different stiffness coefficient.

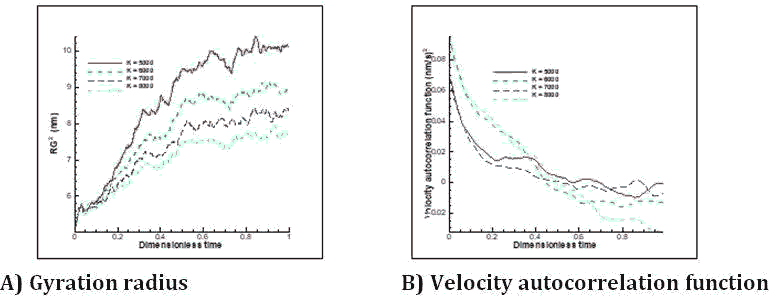
Figure 8: Changes in gyration radius (A) Velocity correlation function (B) Over time in different stiffness (bond coefficient) states for two fixed ends of a polymer chain.

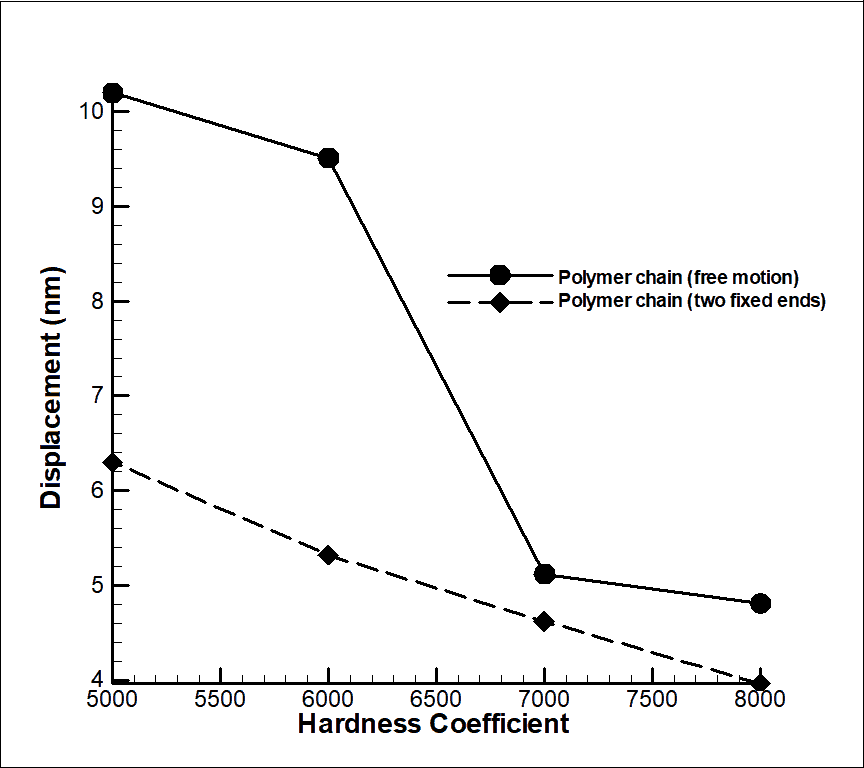
Figure 9: Polymer chain displacements to spring stiffness coefficient between beads for two modes of free movement and restricted movement.

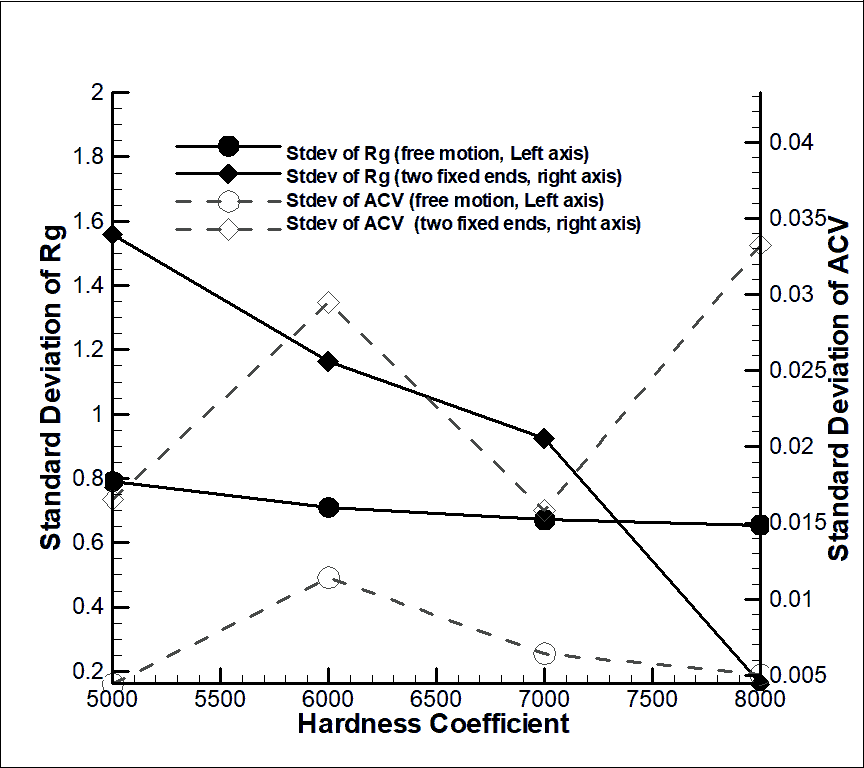
Figure 10: Changes in standard deviation of Gyration Radius (Rg), left axis and Velocity Correlation Function (VACF), right axis according to different stiffness coefficient of polymer chain

Conclusion

In this study, the behavior of a polymer chain in a simple channel was simulated under different conditions of free polymer movement and two fixed ends for a polymer by Dissipation Particle Dynamics (DPD) method. Initially, in order to evaluate the simulation numerical code, the results were evaluated in a simple channel under the influence of constant force in a fully developed state, with analytical results and the accuracy of the results were reported with an error of less than 10%. Next, the polymer chain was placed in a simple channel and the behavior of the polymer chain was investigated and analyzed for 4.5 seconds at a constant force of 0.01. Also, in different cases, the hardness coefficient from 1 to 1.6 times the 5000 hardness coefficient in a time interval of 4.5 seconds was studied. In free movement, about 53% decreases in displacement were observed by increasing the stiffness coefficient by 1.6 times, and the chain was less inclined to twist around itself and it decreased in oscillations of the radius of gyration, and perturbations in the velocity auto correlation function were observed by passing time. In the case of the two fixed ends, with increasing stiffness coefficient, the tendency to stretch decreases and with increasing 1.6 times the stiffness coefficient, about 37% decrease in polymer chain at constant force of 0.01 is obtained. Decreases in gyration radius and turbulence in the velocity correlation function have also been observed. It can be concluded that the DPD method is a powerful method in simulating the motion of micro/nanofluid along with the polymer chain and investigating the complex behavior of the fluid polymer under different condition.

References

1. Manz A, Harrison DJ, Verpoorte EMJ, Fettinger JC, Paulus A, et al. (1992) Planar chips technology for miniaturization and integration of separation techniques into monitoring systems: Capillary electrophoresis on a chip. J Chromatogr 593: 253–258. Crossref, Google Scholar.
2. Woolley AT, Hadley D, Landre P, Demello AJ, Mathies RA, et al. (1996) Functional integration of PCR amplification and capillary electrophoresis in a microfabricated DNA analysis device. Anal Chem 68: 4081–4086. Crossref, Google Scholar, Indexed.
3. Taylor MT, Nguyen P, Ching J, Petersen KE (2003) Simulation of microfluidic pumping in a genomic DNA blood-processing cassette. J Micromech Microeng 13: 201–208. Crossref, Google Scholar, Indexed.
4. Khandurina J, McKnight TE, Jacobson SC, Waters LC, Foote RS, et al. (2000) Integrated system for rapid PCR-based DNA analysis in microfluidic devices. Anal Chem 72: 2995–3000. Crossref, Google Scholar.
5. Jiang L, Mikkelsen J, Koo JM, Huber D, Yao S, et al. (2002) Closed-loop electroosmotic microchannel cooling system for VLSI circuits. IEEE Trans Compon Packag Technol 25: 347–355. Crossref, Google Scholar.
6. Tuckerman DB, Pease RFW (1981) High-performance heat sinking for VLSI. IEEE Electron Device Lett 2: 126–129. Crossref, Google Scholar.
7. Zhang L, Koo JM, Jiang L, Goodson KE, Santiago JG, et al. (2002) Measurements and modeling of two-phase flow in micro channels with nearly constant heat flux boundary conditions. J Microelectromech Sys 11: 12–19. Crossref, Google Scholar.
8. Dash AK, Cudworth GC (1998) Therapeutic applications of implantable drug delivery systems. J Pharmacol Toxicol Methods 40: 1–12. Crossref, Google Scholar, Indexed.
9. Wang EN, Zhang L, Jiang L, Koo JM, Maveety JG, et al. (2002) Micromachined jet arrays for liquid impingement cooling of VLSI chips. J Microelectromech Syst 13: 833-842. Crossref, Google Scholar.
10. Jafari S, Zakeri R, Darbandi M (2018) DPD simulation of non-Newtonian electroosmotic fluid flow in nanochannel. Molecular Simulation 44: 1444-1453. Crossref, Google Scholar.
11. Beskok A, Srinivasa AR (2002) Simulation and analysis of a magnetoelastically driven micro-pump. J Fluids Eng 123: 435–438. Crossref, Google Scholar, Indexed.
12. Accoto D, Carrozza MC, Dario P (2000) Modelling of micropumps using unimorph piezoelectric actuator and ball valves. J Micromech Microeng 10: 277–81. Crossref, Google Scholar.
13. Li X, Pivkin I, Liang H (2013) Hydrodynamic effects on flow-induced polymer translocation through a microfluidic channel. Polymer 54: 4309-4317. Crossref, Google Scholar, Indexed.
14. Xu Z, Yang Y, Zhu G, Chen P, Huang Z, et al. (2019) Simulating transport of soft matter in micro/nano channel flows with dissipative particle dynamics, advanced theory and simulations. Adv Theory Simul 2: 1800160. Crossref, Google Scholar, Indexed.
15. Laser DJ, Santiago JG (2004) A review of micropumps. J Micromech Microeng 14: 35-64. Crossref, Google Scholar.
16. Chen CW, Jiang Y (2019) Computational fluid dynamics study of magnus force on an axis-symmetric, disk-type auv with symmetric propulsion. Symmetry 11: 395-397. Crossref, Google Scholar.
17. Guillouzic S, Slater GW (2006) Polymer translocation in the presence of excluded volume and explicit hydrodynamic interactions. Physics Letters 359: 261-264. Crossref, Google Scholar.
18. Ikonen T, Bhattacharya A, Ala-Nissila T, Sung W (2012) Unifying model of driven polymer translocation. Physical Review E 85: 1-5. Crossref, Google Scholar.
19. Hoogerbrugge P, Koelman J (1992) Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys Lett 19: 153-155. Crossref, Google Scholar.
20. Zhang K, Manke CW (2000) Simulation of polymer solutions by dissipative particle dynamics. Mol Simul 25: 157-166. Crossref, Google Scholar.
21. Willemsen S, Hoefsloot H, Iedema P (2002) Mesoscopic simulation of polymers in fluid dynamics problems. J Stat Phys 107: 53-65. Crossref, Google Scholar.
22. Duong�Hong D, Han J, Wang JS, Hadjiconstantinou NG, Chen YZ, et al. (2008) Realistic simulations of combined DNA electrophoretic flow and EOF in nano�fluidic devices. Electrophoresis 29: 4880-4886. Crossref, Google Scholar.
23. Pan H, Ng TY, Li H, Moeendarbary E (2010) Dissipative particle dynamics simulation of entropic trapping for DNA separation. Sens Actuator A Phys 157: 328-335. Crossref, Google Scholar.
24. Guo J, Li X, Liu Y, Liang H (2011) Flow-induced translocation of polymers through a fluidic channel: A dissipative particle dynamics simulation study. J Chem Phys 134: 1-10. Crossref, Google Scholar.
25. Ranjith SK, Patnaik B, Vedantam S (2014) Transport of DNA in hydrophobic microchannels: A dissipative particle dynamics simulation. Soft matter 10: 4184-4191. Crossref, Google Scholar, Indexed.
26. Zakeri R (2019) Dissipative particle dynamics simulation of the soft micro actuator using polymer chain displacement in electro-osmotic flow. Mol Simul 45: 1488-1497. Crossref, Google Scholar.
27. Groot RD, Warren PB (1997) Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J Chem Phys 107: 4423–4435. Crossref, Google Scholar.
28. Duong-Hong D, Phan-Thien N, Fan X (2004) An implementation of no-slip boundary conditions in DPD. Comput Mech 35: 24–29. Crossref, Google Scholar, Indexed.
29. Nikunen P, Karttunen M, Vattulainen (2003) How would you integrate the equations of motion in dissipative particle dynamics simulations? Computer Physics Communications 153: 407-423. Crossref, Google Scholar.
30. Mao J, Yao Y, Zhou Z, Hu G (2015) Polymer translocation through nanopore under external electric field: dissipative particle dynamics study. Appl Math Mech 36: 1581-1592. Crossref, Google Scholar.
31. Cichocki B, Felderhof BU (1995) Velocity autocorrelation function of interacting brownian particles. Phys Rev E 51: 5549-5555. Crossref, Google Scholar, Indexed.