Editorial, J Phys Res Appl Vol: 1 Issue: 1

Finding a Method for Producing Small Impedance Particles with Prescribed Boundary Impedance is Important

Ramm AG^*

Department of Mathematics, Kansas State University, Manhattan, USA

*Corresponding Author : Alexander G Ramm
Department of Mathematics, Kansas State University, Manhattan, USA
Tel: (785) 532-0580
E-mail: ramm@math.ksu.edu

Received: November 10, 2017 Accepted: November 13, 2017 Published: November 17, 2017

Citation: Ramm AG (2017) Finding a Method for Producing Small Impedance Particles with Prescribed Boundary Impedance is Important. J Phys Res Appl 1:1.

Abstract

Keywords: Scattering theory; Materials science

Introduction

Creating materials with a desired refraction coefficient is a problem of major scientific and technological importance. These materials include meta materials, that is, materials in which group velocity is directed opposite to the phase velocity; materials with a desired radiation pattern, that is materials with a desired scattering amplitudes at a fixed frequency and a fixed incident wave direction. Such materials may scatter the incident plane wave so that most of the energy of the scattered wave goes, for example, in a desired cone. The author developed a theory of wave scattering by many small impedance particles with prescribed boundary impedance [1,10]. This theory allows one to give a recipe for creating materials with a desired refraction coefficient by distributing (with some distribution density) in a given material many small impedance particles with a prescribed boundary impedance. The recipe is formulated in this paper. In order to use it practically one has to solve two technological problems:

1. How to distribute (embed) in a given material many small impedance particles,

and

2. How to produce a small particle with prescribed boundary impedance.

The first of these problems is currently solved.

The aim of this paper is to draw attention of physicists, materials science specialists and engineers to solving the second technological problem. The contents of this paper is very close to the paper of Ramm AG [2], not yet published, and parts of this paper are taken from [2] verbatim. Wave scattering by many small impedance particles is developed in the book of Ramm AG [1], where the basic physical assumption is É�?�? « d « λ. Here ‘É�?�?’ is the characteristic size of the small particles, ‘d’ is the minimal distance between neighboring particles, and λ is the wave length in the medium. It is proved there that if one prepares many small particles with prescribed boundary impedance and embeds these particles (with a specified in [1] distribution density, see formula (7) below) into a given material, then one obtains a material whose refraction coefficient approximates any desired refraction coefficient with an arbitrary small error.

Therefore the basic practical problem of preparing small impedance particles with prescribed boundary impedance is of great interest both technologically and physically.

In section 2 the basic definitions are given. It is explained what a small particle is, what an impedance particle is, what a boundary impedance is. We argue that impedance boundary condition makes physical sense on a particle of arbitrary size and that a small particle with prescribed boundary impedance should exist.

The problem is: how can one produce (manufacture) such a particle practically?

In section 3 a recipe for creating materials with a desired refraction coefficient is formulated. This recipe is taken from the author’s monograph of Ramm AG [1].

Basic Definitions

Let D₁⊂ R³ be a bounded domain with a connected smooth boundary S₁, D′₁ :=R³ \ D′₁ be the unbounded exterior domain and S² be the unit sphere in R³.

Consider the scattering problem:

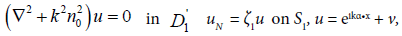(1)

where k > 0 is the wave number, a constant, α ∈ S² is a unit vector in the direction of the propagation of the incident plane wave e^ikα•x, N is the unit normal to S₁ pointing out of D₁, u_N is the normal derivative of u, ζ₁ is the boundary impedance, Imζ₁ ≤ 0, n₀ > 0 is the refraction coefficient of the small impedance particle D₁, n₀ is a constant, the scattered field v satisfies the radiation condition

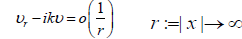(2)

The scattering amplitude A(β,α, k) is defined by the following formula:

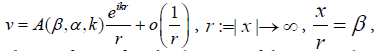(3)

where α, β ∈ S², β is the direction of the scattered wave, α is the direction of the incident wave. A particle of a characteristic size a is called small if it is much smaller than the wave length in the medium, that is, kn₀É�?�? « 1.

The function A(β, α, k) is called the scattering amplitude. It is known (see Ramm AG [3], p.25, or [4], [5]) that the solution to the scattering problem (1)-(3) does exist and is unique.

If there are many (M » 1) small impedance particles Dj, embedded in a bounded domain D filled with material whose refraction coefficient is n₀, then the wave scattering problem can be formulated as follows:

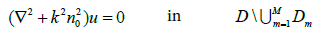(4)

(5)

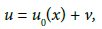(6)

where the scattered field v satisfies the radiation condition, Imζ_m ≤ 0, M is the total number of the embedded particles. The incident field u₀ is assumed known. It satisfies equation (4) in R³, and, as was noted earlier, n₀ = 1 in D’. For simplicity we assume here that all small particles are of the same characteristic size É�?�?. In Ramm AG [1] small particles of various sizes and shapes are allowed.

Let G be the Green’s function of the scattering problem in the absence of the embedded particles. Outside D the refraction coefficient n₀ is assumed to be equal to 1. Assume that the distribution of small particles is given by the formula

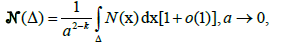(7)

where 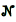(Δ) is the number of particles in an arbitrary open subset of D, N (x) ≥ 0 is a given continuous function, κ ∈ [0, 1) is a number, and the boundary impedance is defined as follows:

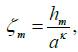(8)

where 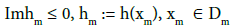is an arbitrary point and h(x) is a given continuous function in D. This function, number κ and the function N (x) can be chosen by the experimenter. It is proved in Ramm AG [1]. p. 48. that the field u in D satisfies, as

É�?�? → 0, the following integral equation:

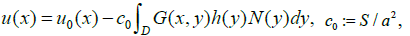(9)

where S is the surface area of a small particle, h(x) and N(x) are defined in (7)-(8). For simplicity we assume here that the surface area S is the same for all small particles. It follows from (9) that the new refraction coefficient in D, which one gets after embedding many small impedance particles, is

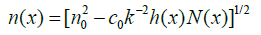(10)

Since h(x) and N (x) are at our disposal, one can get by formula (10) any desirable refraction coefficient, such that Imn²(x) ≥ 0.

Why should the equation (5) make sense physically regardless of the size of the particle?

Because a problem whose solution exists and is unique must have sense physically.

Why should the small impedance particles with prescribed boundary impedance exist?

Because the particles with ζ=∞, acoustically soft particles, do exist, and the particles with ζ=0, acoustically hard particles, do exist, we conclude that small particles with any “intermediate” value of the boundary impedance should also exist.

The problem we raise is:

How can one produce practically (fabricate) such particles?

Recipe for Creating Material with a Desired Refraction Coefficient

Let us formulate the result in the following theorem

Theorem 1. Given n²(x) and a bounded domain D, one can create in D a material with a desired refraction coefficient n(x), Imn²(x) ≥ 0, by embedding 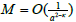small impedance particles according to the distribution law (7). The refraction coefficient 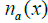corresponding to a finite É�?�?, approximates the desired refraction coefficient n(x) in the sense

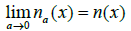(11)

The functions h(x) and N (x) defined in (7)-(8) are found by the Steps 1, 2 of the Recipe formulated below; see also p. 53 in [1].

Finally, let us discuss briefly the possibility to create material with negative refraction coefficient.

By formulas (3.1.1) and (3.1.2) in [3] one gets n(x) < 0 if the argument of 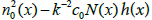is equal to 2π. Assume that 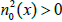We know that 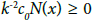Let us take 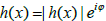where Ï�?�? > 0 is very small, that is, Imh(x) ≥ 0 and Imh(x) is very small. One proves (see also [1], p.52) that equation (9) is uniquely solvable for Imh ≥ 0 sufficiently small. For such h(x) one concludes that the argument 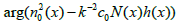is very close to 2π and the square root in (10) is negative, provided that 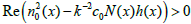. This argument shows that it is possible to create materials with negative refraction coefficient n(x) by embedding in a given material many small particles with properly chosen boundary impedances (6).

A recipe for creating materials with a desired refraction coefficient

Problem 1. Given a material with a known n₀(x) in a bounded domain D and n₀(x) = 1 in D′ one wants to create in D a material with a desired n(x).

Step 1. Given 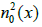and n²(x), calculate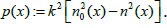

This is a trivial step.

Step 2. Given p(x), calculate h(x) and N (x) from the equation 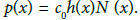The constant c₀ one can take to be c = 4π if the small particles are balls of radius a. This we can assume without loss of generality if we are interested in creating materials with a desired refraction coefficient [1].

There are infinitely many solutions h and N to the above equation [8]. For example, one can fix arbitrarily

N (x) > 0 in D, N (x) = 0 in D′ and find h(x) = h₁(x) + ih₂(x) by the formulas:

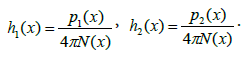
Here p₁(x)= Rep(x) and p₂(x) = Imp(x).

Note that Imn²(x) ≥ 0 implies Imh(x) ≤ 0, so our assumption Imh(x) ≤ 0 is satisfied. For example, one may take N (x) = const > 0.

Step 2 is also trivial.

Step 3. Given N (x) and h(x) = h₁(x) + ih₂(x), distribute 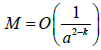small impedance balls of radius a in the bounded region D according to the distribution law (7), where κ ∈ [0, 1) is the number (parameter) that can be chosen by the experimenter. Note that condition d » a is satisfied automatically for the distribution law (7). Indeed, if d is the minimal distance between neighboring particles, then there are at most 1/d³ particles in a cube with the unit side, and since D is a bounded domain there are at most O(1/d³) of small particles in D. On the other hand, by the distribution law (7) one has,

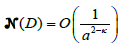
Thus 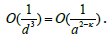Therefore 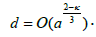Consequently, condition a « d « λ is satisfied, where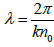

Moreover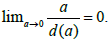

References

1. Ramm AG (2013) Scattering of acoustic and electromagnetic waves by small bodies of arbitrary shape: Applications to creating new engineered materials. Momentum Press, New York, USA.
2. Ramm AG (2017) On the importance of producing small impedance particles with pre- scribed boundary impedance. Thesis, Cornell University Library, New York. 
3. Ramm AG (1986) Scattering by obstacles. D.Reidel, Netherlands.
4. Ramm AG (2005) Inverse problems, Springer, New York, USA.
5. Ramm AG (2017) Scattering by obstacles and potentials. World Scientific, Singapore.
6. Ramm AG (2010) Uniqueness theorem for inverse scattering problem with non-overdetermined data. J Phys A Math Theor 43: 112001.
7. Ramm AG (2010) Uniqueness of the solution to inverse scattering problem with backscattering data. Eurasian Math J 1: 97-111.
8. Ramm AG (2011) Uniqueness of the solution to inverse scattering problem with scattering data at a fixed direction of the incident wave. J Math Phys 52: 123506.
9. Ramm AG (2016) Uniqueness of the solution to inverse obstacle scattering with non-overdetermined data. Appl Math Lett 58: 81-86.
10. Ramm AG (2017) Creating materials with a desired refraction coefficient. Morgan & Claypool Publishers, San Rafael, California, USA.