Research Article, J Phys Res Appl Vol: 1 Issue: 1
Fundamental Investigations of Fermi Surface and Optoelectronic Properties of Pyrochlore Oxide Superconductor (KOs2O6): GGA+U+SOC and DFT
Muhammad Irfan1, Safdar Hussain1, Saleem Ayaz Khan2, Sikander Azam3* and Souraya Goumri-Said4*
1Department of Physics, University of Sargodha, 40100 Sargodha, Pakistan
2New Technologies e Research Center, University of West Bohemia, Univerzitni 8, 306 14 Pilsen, Czech Republic
3Department of Physics, the University of Lahore, 40100 Sargodha, Pakistan
4College of Science, Physics Department, Alfaisal University, P.O. Box 50927, Riyadh, 11533, Saudi Arabia
*Corresponding Authors : Souraya Goumri-Said
College of Science, Physics Department, Alfaisal University, P.O. Box 50927, Riyadh, 11533, Saudi Arabia
Tel: 966-011-215-8984
E-mail: sosaid@alfaisal.edu
Sikander Azam
Department of Physics, The University of Lahore, Pakistan
Tel: (+92)3325794925
E-mail: sikander.physicst@gmail.com
Received: November 08, 2017 Accepted: December 13, 2017 Published: December 18, 2017
Citation: Irfan M, Hussain S, Khan SA, Azam S, Goumri-Said S (2017) Fundamental Investigations of Fermi Surface and Optoelectronic Properties of Pyrochlore Oxide Superconductor (Kos2o6): GGA+U+SOC and DFT. J Phys Res Appl 1:1.
Abstract
We employed first-principle calculations techniques to explore the optoelectronic properties of pyrochlore oxide superconductor named KOs2O6. Due to the existence of localized f and d-states in the electronic configuration of Osmium element, the spin orbit coupling and GGA+U approach were considered in computation in order to describe correctly the d-d coupling. KOs2O6 is a metallic and exhibit a large electrical conductivity as found from Fermi surface. The calculated optoelectronic properties have explored the real and the imaginary parts of the dielectric constant along with the other related optical properties like the refractive index, energy loss function and the absorption along with the reflectivity.
Keywords: Superconductors; Electronic structure; Optoelectronic properties; Fermi surface; FPLAPW; DFT
Introduction
Pyrochlore oxides have demonstrated several interesting phenomena, such as those explored in the metal–insulator transition. They can show colossal magneto resistance, magnetic frustration, and can behave as superconductors, as well as ferroelectrics [1]. The earliest pyrochlore oxide superconductor Cd2Re2O7 having a Currie temperature (Tc=1.0K) was discovered in 2001 showing a predictable Bardeen–Cooper–Schrieffer (BCS-type) superconductivity [2]. Most recently, a novel family of pyrochlore oxide superconductors, AOs2O6, was synthesized and characterized with Tc=3.3, 6.3 and 9.6 K for of A=Cs, Rb and K, respectively [3-5]. Numerous experiments conducted on the pyrochlore oxide (KOs2O6) have reached a superconductivity behavior at maximum critical temperature (Tc). However, some reported deficiencies found in NMR experiments [6] with high coherence peak, have led to measure higher critical field Hc2 ~38T [7]. These results were confirmed by the anisotropic constraint recorded from muon spin rotation (mSR) experiments [8]. Indeed, the investigational outcomes for changing A with Cs or Rb have shown a slight conventional appearance, while the method of superconductivity is expected to be identical for the three compounds [5,6].
The invention of superconductivity inside the b-Pyrochlores increases the complexity of the fundamental method. Whereas the process in Cd2Re2O7, a-pyrochlore [7], is capable of understanding in the weak-coupling BCS supposition of superconductivity [8], Hiroi and collaborators have recommended from the onset that KOs2O6 is an eccentric superconductor, with the combination of arbitrary spin fluctuations [9]. Furthermore, Brühwiler and collaborators [10] recommended that RbOs2O6 possibly will be a predictable BCS-type superconductor, and modern pressure causes dimensions showed to take more support to their results [11]. We specify the closed resemblance among two compounds, it appears improbable that their superconductivity contains dissimilar foundation. Undoubtedly, a cautious learning of the electronic configuration of these materials explained on the bases of superconductivity process.
In this work, we have presented complete study of KOs2O6 solid and carried out a self-consistent ab-initio density-functional calculation of its electrical and optoelectronic, using the fullpotential linearized augmented plane-wave (FLAPW) method. Our calculations are made within the generalized gradient approximation (GGA) to the EXC (exchange-correlation). Due to the existence of localized d-states, we included the spin-orbit coupling (SOC) term and GGA+U approach in order to pronounce correctly the d-d coupling. We observed the dependence of total energy, volume, lattice constants, density of states and optical properties for the KOs2O6.
Computational Details
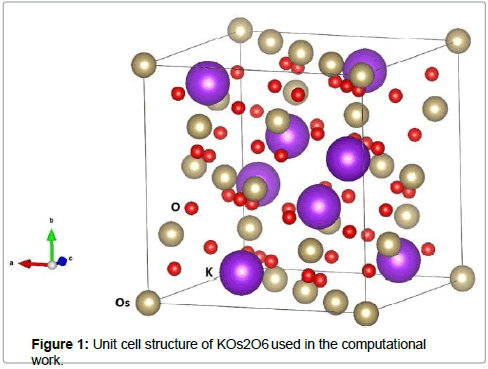
In this work, we used the full- potential linearized augmented plane waves (FPLAPW) method to investigate the physical properties of KOs2O6 with WIEN2k package [12]. The PBEsol GGA (generalized gradient approximation) [13] is used for the exchange correlation prospective. RMT represents the least muffin-tin radius, Kmax is the cut off vector of the plane wave, and in the interstitial region RMTX Kmax=8. The magnitude of principal vector in the charge density Fourier expansion has relation Gmax=16 Ry1/2 and angular momentum contains the value 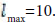 . The core cut of energy is described by the valence and core separation, chosen as -6.0 Ry depressed by of spin- orbit interaction. When the total energy reaches to 10– 5 Ry, so iteration was finished. The optical scheming reveals a denser k- mesh for the convergence, so a fine k-mesh 12×12×12 was selected. We treated the exchange correlation (Exc) within the GGA (generalized gradient approximation) along with the effective Hubbard parameter, U=7.0 eV. Herein we also considered the spin–orbit coupling (SOC) due to the Os (Osmium) heavy metal using the variational approach [14,15]. For the ab-initio calculations the crystallographic parameters of KOs2O6 were taken from the experimental J.-I. Yamaura et al. work of the [16]. The structure of KOs2O6 crystallizes in a cubic structure with SG (space group) number 227 (Fd−3m) with lattice constant a = b = c = 10:089 (2) Å, and has 18 atoms per unit cell: two K (8b), four Os (16c), and twelve O (48f) which is demonstrated in Figure 1. The K, Os and O atoms are positioned at (fractional coordinates) 0.375 0.375 0.375, 0.0, 0.0, 0.0 and 0.3145(8) 0.125 0.125. Using the Murnaghan equation [17] we studied the ground states properties like lattice constant, bulk modulus and its derivative with respect to pressure by fitting total energy correspond to unit cell volume. Our calculated relaxed and optimized lattice parameters compared to experimentally deduced lattice parameters [16] are listed in Tables 1 and 2. These results agree well with the experimental data reported [16].
. The core cut of energy is described by the valence and core separation, chosen as -6.0 Ry depressed by of spin- orbit interaction. When the total energy reaches to 10– 5 Ry, so iteration was finished. The optical scheming reveals a denser k- mesh for the convergence, so a fine k-mesh 12×12×12 was selected. We treated the exchange correlation (Exc) within the GGA (generalized gradient approximation) along with the effective Hubbard parameter, U=7.0 eV. Herein we also considered the spin–orbit coupling (SOC) due to the Os (Osmium) heavy metal using the variational approach [14,15]. For the ab-initio calculations the crystallographic parameters of KOs2O6 were taken from the experimental J.-I. Yamaura et al. work of the [16]. The structure of KOs2O6 crystallizes in a cubic structure with SG (space group) number 227 (Fd−3m) with lattice constant a = b = c = 10:089 (2) Å, and has 18 atoms per unit cell: two K (8b), four Os (16c), and twelve O (48f) which is demonstrated in Figure 1. The K, Os and O atoms are positioned at (fractional coordinates) 0.375 0.375 0.375, 0.0, 0.0, 0.0 and 0.3145(8) 0.125 0.125. Using the Murnaghan equation [17] we studied the ground states properties like lattice constant, bulk modulus and its derivative with respect to pressure by fitting total energy correspond to unit cell volume. Our calculated relaxed and optimized lattice parameters compared to experimentally deduced lattice parameters [16] are listed in Tables 1 and 2. These results agree well with the experimental data reported [16].
| X | Y | Z | ||||
|---|---|---|---|---|---|---|
| Exp. | Opt. | Exp. | Opt. | Exp. | Opt. | |
| K | 0.375 | 0.391 | 0.375 | 0.391 | 0.375 | 0.391 |
| Os | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| O | 0.3145(8) | 0.3186 | 0.125 | 0.127 | 0.125 | 0.127 |
Table 1: Comparison between experimental and optimized atomic positions for KOs2O6.
| Os–O (Å) | O–Os–O (˚) | Os–O–Os (˚) | |||
|---|---|---|---|---|---|
| Exp. | Opt. | Exp. | Opt. | Exp. | Opt. |
| 1.898(3) | 1.912 | 90.8(3)/89.2(3) | 91.05/89.9 | 139.9(4) | 141.02 |
Table 2: Selected bond lengths (Å) for KOs2O6 resulting from relaxation of the unit cell and compared to the experimental data [16].
Results and Discussion
Electronic structure
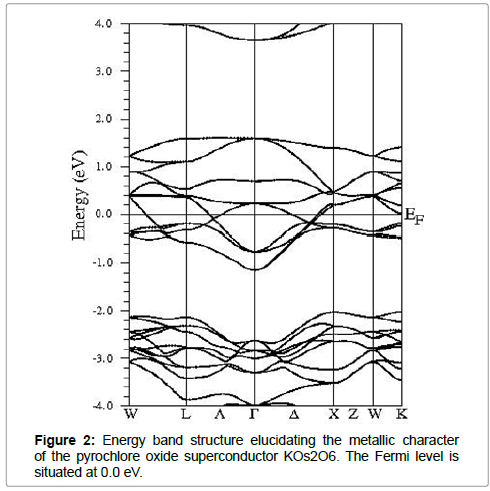
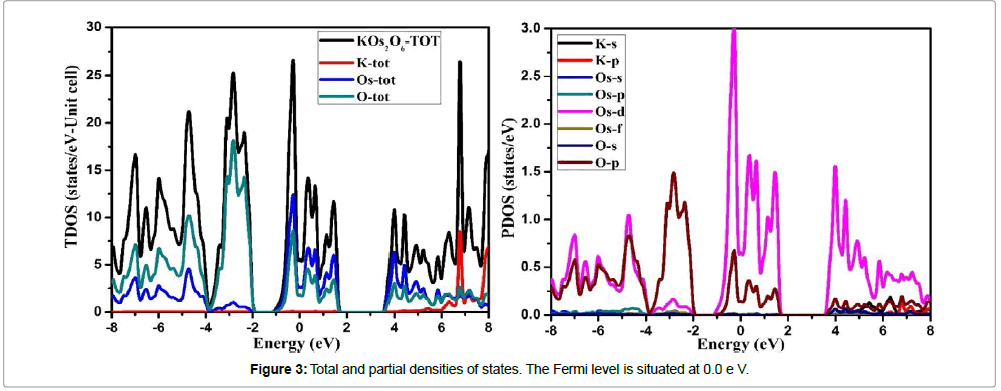
Our investigated material has localized d states electrons, so the SOC (spin orbit coupling) cannot be overlooked. Therefore the electronic structure for the KOs2O6 cannot be explained by simple GGA functional. Hence GGA+U along with the SOC approach is used successfully in strong correlated systems to state appropriately the d-d coupling. The calculated energy band structure of KOs2O6 is demonstrated in Figure 2. As can be seen that band structure display no band gap at the EF (Fermi level) that confirms the metallic behavior. Figure 3 shows the total and partial densities of states (TDOS/PDOS) for the KOs2O6 material within GGA+SOC+U (U=6.0 eV) approach in the energy range -8.0 to 8.0.0 eV. As we have included the U parameter to GGA, clearly one can observe a large splitting in Os-d states. By using the GGA+U+SOC, we also calculated the NEF (density of electrons) at the Fermi level along with the electronic specific heat, 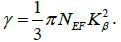
As the electronic specific heat depends only on the NEF, with the factor that all other terms are constant. The calculated value for the investigated material is 4.7 (mJ/moleK2). The PDOS (partial densities of states) that are shown in Figure 3b confirmed the influence of GGA+U+SOC correlation on the Os-5d6 states. The U (Hubbard) parameter split the Os-5d6 states into both states i.e., in occupied and unoccupied states, as a result of EF (Fermi level). The band, mainly the p states of O atom shows hybridization with Os atom around Fermi level (valence band). Contributions of s and p states of K at the Fermi level and in the occupied states are negligible. The lower part of the VB (valence band) between -8.0 ~ -4.0 eV is mainly due to the s and p states of O. Whereas in between -4.0 ~ Fermi level and around the it the main contributions come from the s and p states of O and Os atom along with the Os-d contribution. The d states of Os of and p states of O atom located between the Fermi level and -4.0 eV show a strong interaction between them. Also, we observed a robust contribution of Os-d and O-p states to DOS along the whole energy axis in the conduction band.
Fermi surfaces
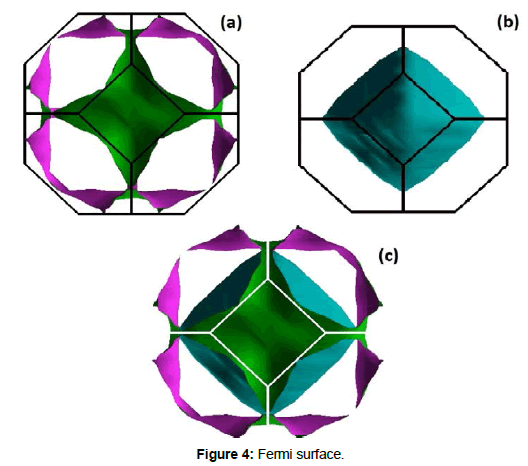
To complete the explanation and elucidate the electrical as well as the optical characteristics due to the electronic configuration we have computed the Fermi surfaces (FS) for the accessible electronic orbital in KOs2O6 as displayed in Figures 4a, 4b and 4c. Furthermore, the Fermi surface is useful to get improved information of the states crossing the Fermi level. In the present material, the orbitals which are crossing the Fermi level beside the Γ−F route are 101 to 102, located in 2D Fermi surfaces and these FS contains two sheets (i.e. these sheets match to the numbers of bands cross the Fermi level in the absolute compound). Also, these FS are having an electronic sheets and set of holes. The vacant region includes holes and the shaded area is prepared up of electrons. The conductivity in the examined compounds is approximately dissimilar from each other as it is obvious commencing the FS iso-surfaces. Moreover, the color amended in FS takes place due to the alteration in electron velocity. The red and violet colors are indicated fast electrons while the slow velocities of electrons are exhibited with the residual color, owing to the intermediary velocity of electrons. It is understandable from our topological investigation of FS that the present material is showing a good electrical conductivity due its metallic character. As result, the computed FS were very helpful to investigate the job of electrons in the scheme, whose topology is immediately connected to the transport properties of materials and mostly to the electrical conductivity.
Optical properties
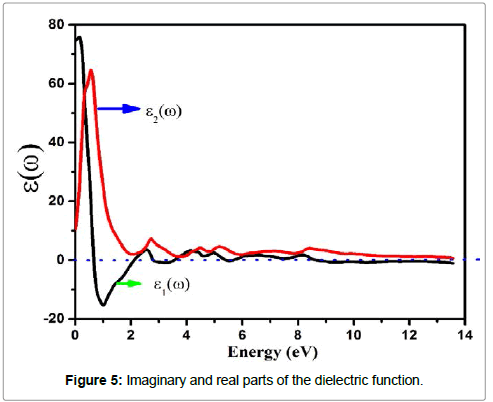
The optical response of the system can be investigated by dielectric constant in the presence of external electric field. The relation for dielectric constant is expressed by: ε(ω)=ε1(ω) +ε2(ω), where the real part, ε1(ω) shows dispersive nature through the material surface and imaginary part 2(ω) illustrate light absorption of the material. In the present approximation excitonic effects are ignored but local field effect is considered. The interband and interaband transitions are contributed in ε(ω). For metals only the contribution from interaband transitions is significant. The interband transitions can further divided into direct and indirect transitions, which engage scattering of phonons and predictable to give only small contribution ofε(ω). The momentum matrix elements have been calculated on a grid of 3000 special k- points for KOs2O6. The imaginary part of dielectric function ε2(ω) is used to analyze interband contribution by sum of all possible transitions from unoccupied and occupied states. The imaginary part can be analyzed by the formula
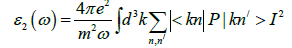
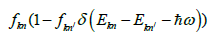 (2)
(2)
Where m is mass, e is electron charge, ω is the volume, hω the energy of incident phonon, P is momentum operator, fkn/ is the Fermi distribution, and |kn\> represents crystal wave function. The matrix element can be evaluated from Eq. 1 by MT and interstitial regions separately. More details about the calculation matrix element s are given elsewhere [18]. The summary over the BZ in Eq.1 is performed by linear interpolation on a network of uniformly disseminated points, the tetrahedron method [19]. The imaginary part of dielectric function 2(ω) is analyzed in the irreducible part of the BZ. The dielectric function is a tensor, and computation of all components is complex one. So we must initiate correct symmetry of the crystal to decrease the number of components. For cubic structure, we require to compute xx=yy=zz component of total dielectric function. For KOs2O6 structure [α=β=γ=90°], the dielectric tensor is then
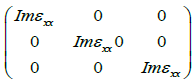
Hence, we get dielectric functions resolved into one Cartesian component. Moreover this decomposition remains valid for all optical constants given afterward. The real part of complex dielectric function is computed by Kramer-kroning relation, while imaginary part is calculated by addition of all allowed intensities in occupied and unoccupied states. If we have complex dielectric function we can compute some other parameters like absorption coefficient, refractive index, reflectivity and extinction coefficient etc.
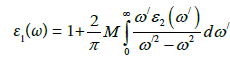
Where M is represents the principle value of the integral.
The optical constants i.e. refractive index n(ω), and extinction coefficient K(ω), are observed from the real and imaginary parts of the complex dielectric function as [20,21]
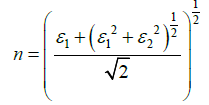 (3)
(3)
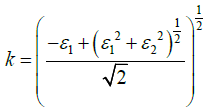 (4)
(4)
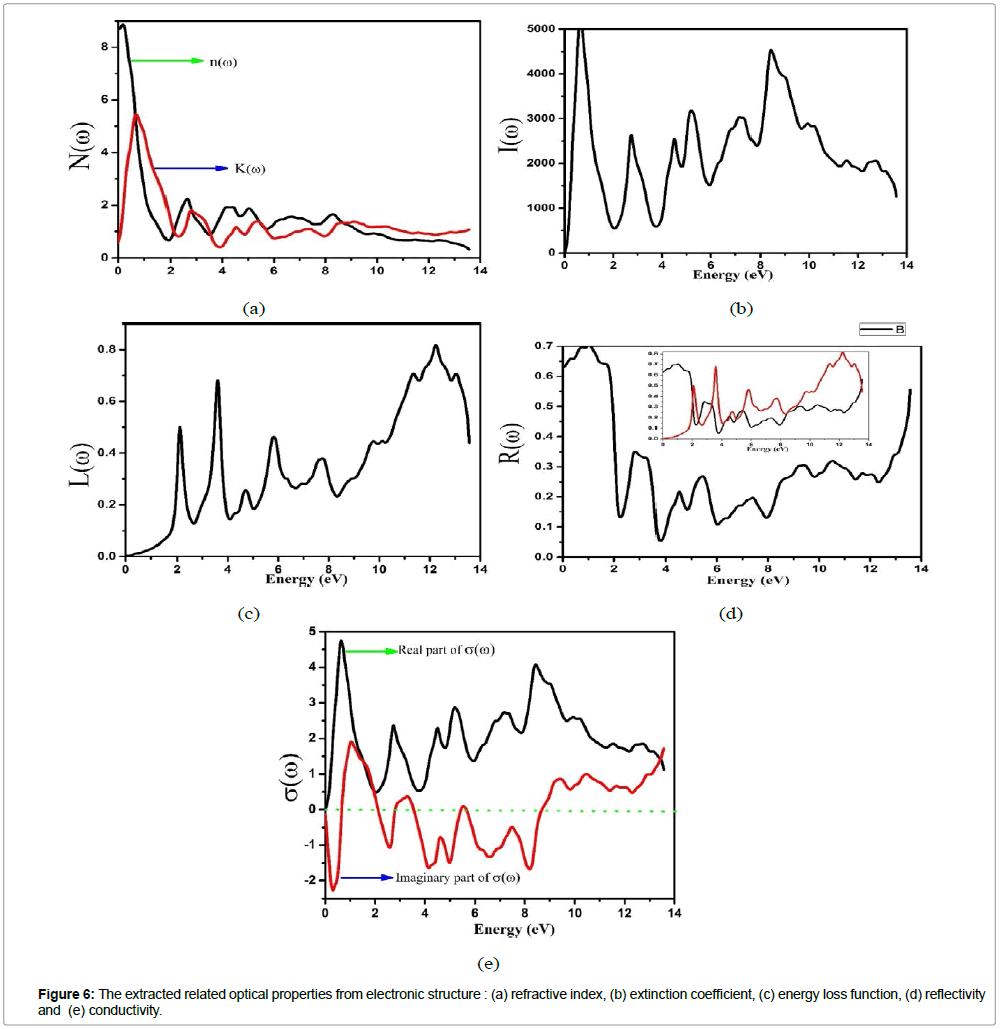
Moreover, the other optical parameters, such as absorption coefficient I(ω), reflectivity R(ω), and energy loss function L(ω) are derived from ε1(ω) and ε2(ω) [22]. For the optical properties of KOs2O6, we select a fine k- mesh (extra k points than selected for SCF cycle). In this work, we have found good quality results for 690 kpoints in IBZ, which resulted from 3000 k- points in BZ. The optical structure of KOs2O6 observed accurately by applying GGA+U+SOC functional on k- points of 12×12×12 order. Figures 5 and 6(a-e) indicate the plots of energy range [0-14] eV, of the real and imaginary parts of ε(ω)and related optical properties respectively. It is observed from the calculated spectra of ε1(ω) that the zero frequency ε1(0) depends upon energy band gap. As the under investigated material has the metallic nature so the absorption starts from 0.0 eV and its value of ε1(0) = 76.0. After that it reduces and goes to negative around 1.0 eV and attain the zero value above 2.0 eV. The value of ε1(ω) is negative in between 1.0 – 2.6 eV. The negative value of ε1(ω) reveals that incident light is reflected totally from the surface of material, which shows the metallic nature of the samples. The main parameter for the design of optoelectronic devices is imaginary part of dielectric function. The energy band gap and maximum absorption intensity of light in a specific region can be computed by using ε2(ω). The maximum value of ε2(ω) arise at energy less than 0.5 eV. After this it decreases and finally reaches the zero. The refractive index and extinction coefficient are calculated from the following relations ε1(ω)= n2-k2 and ε2(ω)= 2nk . Figure 6a, represents the graphical analysis of the n(ω), k(ω) , where they exhibit the same behavior as the dielectric constants ε1(ω),ε2(ω). Moreover 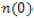 , and ε1(0) satisfy the relation n 2 0=ε1(0) and agreed well with our optimized result. In addition n(ω)is dimensionless and shows the propagation of energy in the matter. n(ω) varies with wavelength of light due to dispersion, from which light splits its constituent colours. The value of n(ω), must be higher in the optical field and most of the materials have in the range of one and two. In our observation, the maximum value of n(ω) for is > 0.5 eV. The peaks of plot disappear at the higher energy. It means that transparency of materials decreases at higher energy, and due to band transition (valence to conduction) high energy photons are absorbed. The value of n(ω) less than unity in the region 10-14 eV. Moreover, it is observed from the fractional refractive index that the group velocity is higher than speed of light, and this velocity shifts to negative values. This behavior might lead to consider the present material for non-linear response. For the surface analysis of the samples reflectivity (Figure 6b) is also computed, which is the difference of the incident and reflected power as describe in the Figure 6a, its value at zero frequency limit R(0) is 64 %. The peaks of R(ω) is analogous to the peaks ε1(ω). So the value reflectivity R(ω) is maximum in the region where absorption coefficient covers minimum value. Furthermore, there are large numbers of peaks laying in the spectrum region lower energy range. It is more surprising that maximum value of R(ω) and minimum value of ε1(ω) investigated in the same region. This is due to fact, that in the metallic portion all incident radiations are reflected and the band gap is zero, lacking absorption of incident light. In the inset of Figure 6d, we can see that at the point where we have increase in the reflectivity we have at that point we have decrease in the energy loss function (see Fig 6c). k(ω) and ε2(ω) have same nature, and are very useful to find the absorption of light and band edge by using the relation
, and ε1(0) satisfy the relation n 2 0=ε1(0) and agreed well with our optimized result. In addition n(ω)is dimensionless and shows the propagation of energy in the matter. n(ω) varies with wavelength of light due to dispersion, from which light splits its constituent colours. The value of n(ω), must be higher in the optical field and most of the materials have in the range of one and two. In our observation, the maximum value of n(ω) for is > 0.5 eV. The peaks of plot disappear at the higher energy. It means that transparency of materials decreases at higher energy, and due to band transition (valence to conduction) high energy photons are absorbed. The value of n(ω) less than unity in the region 10-14 eV. Moreover, it is observed from the fractional refractive index that the group velocity is higher than speed of light, and this velocity shifts to negative values. This behavior might lead to consider the present material for non-linear response. For the surface analysis of the samples reflectivity (Figure 6b) is also computed, which is the difference of the incident and reflected power as describe in the Figure 6a, its value at zero frequency limit R(0) is 64 %. The peaks of R(ω) is analogous to the peaks ε1(ω). So the value reflectivity R(ω) is maximum in the region where absorption coefficient covers minimum value. Furthermore, there are large numbers of peaks laying in the spectrum region lower energy range. It is more surprising that maximum value of R(ω) and minimum value of ε1(ω) investigated in the same region. This is due to fact, that in the metallic portion all incident radiations are reflected and the band gap is zero, lacking absorption of incident light. In the inset of Figure 6d, we can see that at the point where we have increase in the reflectivity we have at that point we have decrease in the energy loss function (see Fig 6c). k(ω) and ε2(ω) have same nature, and are very useful to find the absorption of light and band edge by using the relation 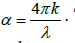 The peaks of k(ω) and n(ω) are showing tendency from valence to conduction band, which occur due to a direct transition. The α (absorption coefficient) is very prominent parameter, used to approximate the decaying rate of intensity per unit band gap and distance of the investigating material. The maximum value of α lies in the selected energy range between 0.0 ~ 14.0 eV, which is shown in the inset of Figure 6d. Figure 6e shows the optical conductivity σ(ω)for KOs2O6. As we are dealing with a metallic material so the absorption starts from 0.0 eV. From the plots it is shown that σ(ω) reaches its highest values in 0.5 ~ 10.0 eV ranges and then drops to smallest amount with supplementary growth in the photon energy. Consequently it is analyzed that all peaks, particulars of σ(ω)coincide with the peaks of α for both compounds, in the deliberated range of energy. So the σ(ω) occurs in these compounds due to the absorption in the first BZ one beside high symmetry points.
The peaks of k(ω) and n(ω) are showing tendency from valence to conduction band, which occur due to a direct transition. The α (absorption coefficient) is very prominent parameter, used to approximate the decaying rate of intensity per unit band gap and distance of the investigating material. The maximum value of α lies in the selected energy range between 0.0 ~ 14.0 eV, which is shown in the inset of Figure 6d. Figure 6e shows the optical conductivity σ(ω)for KOs2O6. As we are dealing with a metallic material so the absorption starts from 0.0 eV. From the plots it is shown that σ(ω) reaches its highest values in 0.5 ~ 10.0 eV ranges and then drops to smallest amount with supplementary growth in the photon energy. Consequently it is analyzed that all peaks, particulars of σ(ω)coincide with the peaks of α for both compounds, in the deliberated range of energy. So the σ(ω) occurs in these compounds due to the absorption in the first BZ one beside high symmetry points.
Conclusion
We employed the first-principle approach that is based on the DFT (density functional theory) method with GGA+U+SOC (spin-orbit coupling), to explore the electronic and optoelectronic properties of pyrochlore oxide superconductor KOs2O6. The ground state properties that are based on the internal structure parameters, like lattice constants and bulk modulus were comprehended from the structural relaxation and optimization. The employed computational approach (i.e., GGA+U+SOC) produced a correct description of the structural parameters along with the electronic properties. We have also studied the Fermi surface shape to assess their behaviors. We also focused on the optoelectronic properties in which we studied the dielectric function like the real and the imaginary parts along with the other related optical properties. As KOs2O6 has a metallic nature therefore the inter-band and intra-band transitions are contributed in ε(ω). For metals only the contribution from intra-band transitions is significant. There have been no previous experimental or theoretical results for the electronic optical properties available for the present pyrochlore oxide superconductor KOs2O6. These outcomes of the current study can be considered as a prediction study with the hope that it will stimulate other research on these materials.
References
- Subramanian MA, Aravamudan G, Rao GVS (1983) Oxide pyrochlores- A review. Prog Solid State Chem 15: 55-143.
- Hanawa M, Muraoka Y, Tayama T, Sakakibara T, Yamaura J, et al. (2001) Superconductivity at 1 K in Cd2Re2O7. Phys Rev Lett 87: 187001.
- Yonezawa S, Muraoka Y, Matsushita Y, Hiroi Z (2004) Superconductivity in a pyrochlore-related oxide KOs2O6. J Phys Condens Matter 16: L9-L12.
- Yonezawa S, Muraoka Y, Matsushita Y, Hiroi Z (2004) New Pyrochlore Oxide Superconductor RbOs2O6. J Phys Soc Jpn 73: 819-821.
- Yonezawa S, Muraoka Y, Hiroi Z (2004) New β-Pyrochlore Oxide Superconductor CsOs2O6. J Phys Soc Jpn 73: 1655-1656.
- Brühwiler M, Kazakov SM, Zhigadlo ND, Karpinski J, Batlogg B (2004) Superconductivity in the geometrically frustrated pyrochlore RbOs2O6. Phys Rev B 70: 020503.
- Hanawa M, Muraoka Y, Tayama T, Sakakibara T, Yamaura J, Hiroi Z (2001) Superconductivity at 1 K in Cd2Re2O7. Phys Rev Lett 87: 187001.
- Hiroi Z, Yonezawa S, Muraoka Y (2004) Unprecedented Superconductivity in β-Pyrochlore Osmate KOs2O6. J Phys Soc Jpn 73: 1651-1654.
- Koda A, Higemoto W, Ohishi K, Saha SR, Kadono R, et al. (2005) Possible Anisotropic Order Parameter in Pyrochlore Superconductor KOs2O6 Probed by Muon Spin Rotation. J Phys Soc Jpn 74: 1678-1681.
- Yonezawa S, Muraoka Y and Hiroi Z (2004) New β-Pyrochlore Oxide Superconductor CsOs2O6. J Phys Soc Jpn 73: 1655-1656
- Hiroi Z, Hanawa M (2002) Superconducting properties of the pyrochlore oxide Cd2Re2O7. J Phys Chem Solids 63: 1021-1026.
- Blaha P, Schwarz K, Madsen GKH, Kvasnicka D, J Luitz (2001) WIEN2K, An augmented plane wave + local orbitals program for calculating crystal properties. Thesis, Technische Universität Wien, Austria.
- Perdew JP, Ruzsinszky A, Csonka GI, Vydrov OA, Scuseria GE, et al. (2008) Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys Rev Lett 100:136406.
- Bendjedid A, Seddik T, Khenata R, Baltache H, Murtaza G, et al. (2015) GGA+U study on phase transition, optoelectronic and magnetic properties of AmO2 with spin–orbit coupling. J Magn Magn Mater 396: 190-197.
- Azam S, Khan SA, Minar J, Khan W, Din H, et al. (2015) Coulomb interaction and spin-orbit coupling calculations of thermoelectric properties of the quaternary chalcogenides Tl2PbXY4 (X = Zr, Hf and Y = S, Se). Semicond Sci Technol 30: 105018.
- Yamaura J, Yonezawa S, Muraoka Y, Hiroi Z, et al. (2006) Crystal structure of the pyrochlore oxide superconductor KOs2O6. J Solid State Chem 179 336-340.
- Murnaghan FD (1944) The Compressibility of Media under Extreme Pressures. Proc Natl Acad Sci U S A 30: 244-249.
- Ambrosh-Draxl C, Sofo JO (2006) Linear optical properties of solids within the full-potential linearized augmented planewave method. Comput Phys Commun 175: 1-14.
- Blochl PE, Jepsen O, Andersen OK (1994) Improved tetrahedron method for Brillouin-zone integrations. Phys Rev B 49:16223.
- Delin A, Eriksson AO, Ahuja R, Johansson B, Brooks MS, et al. (1996) Optical properties of the group-IVB refractory metal compounds. Phys Rev B 54: 1673.
- Amin B, Ahmad I, Maqbool M, Goumri-Said S, Ahmad R (2011) Ab initio study of the bandgap engineering of Al1−xGaxNAl1−xGaxN for optoelectronic applications. J Appl Phys 109: 023109.
- Saha S, Sinha TP, Mookerjee A (2000) Electronic structure, chemical bonding, and optical properties of paraelectric BaTiO3. Phys Rev B 62: 8828.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi