Mini Review, J Phys Res Appl Vol: 7 Issue: 4

Historical Journey of the Fast Fourier Transform-From Enlightenment Europe via Bletchley Park to the Modern World

Keith John Jones^*

Consultant Mathematician (Retired), Weymouth, Dorset, UK

*Corresponding Author: Keith John Jones
Consultant Mathematician (Retired), Weymouth, Dorset, UK
E-mail: keith.jones8@talktalk.net

Received date: 25 November, 2023, Manuscript No. JPRA-23-121188;

Editor assigned date: 27 November, 2023, Pre QC No. JPRA-23-121188 (PQ);

Reviewed date: 11 December, 2023, QC No. JPRA-23-121188;

Revised date: 18 December, 2023, Manuscript No. JPRA-23-121188 (R);

Published date: 25 December, 2023, DOI: 10.4172/JPRA.1000048.

Citation: Jones KJ (2023) Historical Journey of the Fast Fourier Transform-From Enlightenment Europe via Bletchley Park to the Modern World. J Phys Res Appl 7:4.

Abstract

Keywords:

DFT; FFT; History

Introduction

The subject of spectrum analysis started in earnest with work of Joseph Fourier (1768-1830), who asserted and proved that an arbitrary function could be transformed into a sum of trigonometric functions. It seems likely, however, that such ideas were already common knowledge amongst European mathematicians by the time Fourier appeared on the scene, mainly through the earlier work of Leonard Euler (1707-1783) and Joseph Louis Lagrange (1736-1813), with the first appearance of the discrete version of this transformation, the Discrete Fourier Transform (DFT), dating back to Euler’s investigations of sound propagation in elastic media in 1750 and to the astronomical work of Alexis Claude Clairut (1713-1765) in 1754 [1]. Today, due to the suitability of the frequency domain for convolutionbased filtering operations, the DFT plays a central role in many disciplines, including signal/image processing and computer vision.

Turning to its definition, the DFT is a unitary transform, which for the case of N input/output samples, may be expressed in normalized form via the equation

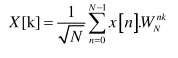
for k=0,1, .…, N-1 where the transform kernel – also known as the Fourier matrix – derives from the term

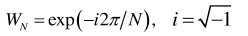
the primitive N^th complex root of unity [2]. The direct computation of the DFT involves O(N2) arithmetic operations, so that many of the early scientific problems involving it’s use could not be seriously attacked without access to fast algorithms for its efficient solution. The key to designing such algorithms is the identification and exploitation of symmetries – through the application of suitable number theoretic and/or algebraic techniques – whether the symmetries exist in just the transform kernel or the input/output data as well.

Literature Review

One early area of activity for the DFT involved astronomical calculations and in the early part of the 19th century Carl Friedrich Gauss (1777-1855) used it for the interpolation of asteroidal orbits from equally-spaced sets of observations [1]. He developed a fast twofactor algorithm for its computation that was identical to that described in 1965 by James Cooley and John Tukey – as with many of Gauss’s greatest ideas, however, the algorithm wasn’t published outside of his collected works and only then in an obscure Latin form. This algorithm, which for a transform of length N=N1×N2 involves just O((N1+N2).N) arithmetic operations, was probably the first member of the class of algorithms now commonly referred to as the Fast Fourier Transform (FFT), which is unquestionably the most ubiquitous algorithm in use today for the analysis of digital data. In fact, Gauss is known to have first used the above-mentioned algorithm as far back as 1805, the same year that Admiral Nelson routed the French fleet at the Battle of Trafalgar – interestingly, Fourier served in Napoleon Bonaparte’s army from 1798 to 1801, during its invasion of Egypt, acting as scientific advisor.

Pioneering work was later carried out in the early 20^th century by the German mathematician Carl Runge, who in 1903 recognized that the periodicity of the DFT kernel could be exploited to enable the computation of a 2N-point DFT to be reduced to that of two N-point DFTs, this factorization technique being subsequently referred to as the doubling algorithm. The Cooley-Tukey algorithm, which does not rely upon any specific factorization of the transform length, may thus be viewed as a simple generalization of this algorithm, as successive application of the doubling algarithm leads directly to the radix-2 version of the Cooley-Tukey algorithm which involves just O(N.log₂N) arithmetic operations. Runge’s influential work was subs- equently picked up and popularized in publications by Karl Stumpff in 1939 and Gordon Danielson and Cornelius Lanczos in 1942, each in turn making contributions of their own to the subject.

Danielson and Lanczos, for example, produced reduced-complexity solutions by exploiting symmetries in the transform kernel, whilst Stumpff discussed versions of both the doubling and the related tripling algorithm [3-7].

Discussion

All the techniques developed, including those of more recent origin such as the nesting algorithm of Schmuel Winograd from 1975 (which exploits his own minimum-complexity small-DFT routines) and the split-radix algorithm of Pierre Duhamel from 1984, rely upon the familiar divide-and-conquer principle, whereby the computation of a composite-length DFT is broken down into that of a number of smaller DFTs where the small-DFT lengths correspond to the factors of the original transform length. Depending upon the particular factorization of the transform length noting, from the Fundamental Theorem of Arthmetic, that any integer greater than 1 can be uniquely factored into a product of primes [2] - this process may be repeated in a recursive fashion on the increasingly smaller DFTs [8,9].

The class of fast algorithms based upon the decomposition of a composite-length DFT into smaller DFTs whose lengths have common factors – such as the Cooley-Tukey algorithm – is known as the Common Factor Algorithm (CFA). When the small-DFT lengths are relatively prime, however, it becomes known as the Prime Factor Algorithm (PFA) [2,4]. The CFA requires that the intermediate results obtained between successive stages of small DFTs be multiplied by elements of the Fourier matrix, these terms commonly referred to as twiddle factors. For the case of the PFA, however, there is no such requirement as the resulting twiddle factors each equate to one. This attractive algorithm, which greatly extends the range of admissible transform lengths, arose through the development of a new data reordering scheme in 1958 by statistician Jack Good [10]. The scheme is based upon the ubiquitous Chinese Remainder Theorem – which provides a means of obtaining a unique solution to a set of simultaneous linear congruences – whose origins supposedly date back to the mathematician Sun Zi from the 1st century A.D. [11].

With regard to the various developments in FFT design that have taken place, it is the names of Cooley and Tukey that are invariably mentioned in any historical account. This does not really do justice, however, to the many previous contributers whose work was simply not picked up on, or appreciated, at the time of publication. The prime reason for such a situation was the lack of a suitable technology for their efficient implementation, this remaining the case until the arrival of the semiconductor revolution.

We return now to Good as his background is a fascinating one for anyone interested in the history of computing. During World War II he served at Bletchley Park, in Buckinghamshire, working alongside Alan Turing on, amongst other things, the decryption of messages produced by the Enigma machine as used by the German armed forces. At the same time, on the same site, a team of engineers under the leadership of Tom Flowers – all seconded from the Post Office Research Establishment at Dollis Hill in North London – were, unbeknown to the outside world, developing the world’s first electronic computer, the Colossus, under the supervision of Turing and Cambridge mathematician Max Newman. The colossus was built primarily to automate various essential code breaking tasks such as the cracking of the Lorenz code used by Adolf Hitler to communicate with his generals [12,13].

Jack Good – later to work with Turing and Newman at Manchester University on a successor to Colossus, the Manchester Mark I – therefore had direct involvement not only with the development of the FFT but also with that of the very technology that makes it such a crucially important algorithm today. The Colossus was the first serious device – albeit a very large and specialized one – on the pa th towards our current state of technology whereby the FFT may be mapped onto ever-smaller silicon devices for use in an ever-increasing number of applications ranging from astronomy and optics to mobile communications and cryptography. However, the parallel computing capabilities resulting from the recent technological innovations has necessitated a fundamental change in how we assess the complexity of the FFT, with straightforward arithmetic operation counts being replaced by new metrics such as those discussed by Jones relating to power consumption or computational density [14,15].

Conclusion

Thus, the journey of the FFT has been traced from its origins in Enlightenment Europe, via an unusual connection at Bletchley Park, to its unique place in the technological world of today. Moving into the future, intelligent FFT designs able to exploit the increasing levels of parallelism made available by modern computing technology – such as that provided by the Field-Programmable Gate Array (FPGA) – might enable one, for example, to: a) handle large multi-dimensional transforms, as typically required for the continuous real-time processing of multi-dimensional images; or, with the potential opportunities offered by those quantum computing technologies currently being developed, to b) assist with implementing Shor’s algorithm (concerning the factorization of ‘extremely’ large integers) on a quantum computer, thus offering the potential for breaking existing public-key cryptography schemes [16-20].

With problems such as these to address, both researchers and practitioners alike should find much to delight. The key, underlying requirement, in achieving success in these endeavors will be the effective application of mathematic techniques, both old and new:

“For the things of this world cannot be made known without knowledge of mathematics”.

Roger Bacon (1214-1294), English philosopher & scientist [21].

Conflicts of Interest

The author states that there are no conflicts of interest.

References

1. Heideman M, Johnson D, Burrus C (1984) Gauss and the history of the fast Fourier transform. IEEE ASSP Mag 1(4):14-21.

   [Crossref][Google Scholar]

2. Birkhoff G, Mac Lane S (2017) A survey of modern algebra. CRC Press.
3. Cooley JW, Tukey JW (1965) An algorithm for the machine calculation of complex Fourier series. Math Comput 19(90):297-301.

   [Google Scholar]

4. Brigham EO (1988) The fast Fourier transform and its applications. Prentice-Hall, Inc.; Jul 1.

   [Crossref][Google Scholar]

5. Runge C (1903) Uber die Zerlegung Empirisch Periodischer Funktioner in Sinnus-Wellen, Zeit. Fur Math und Physik 48:443-456.

   [Crossref][Google Scholar]

6. Stumpff K (1939) Tafeln und Aufgaben zur harmonischen Analyse und Periodogrammrechnung. Springer-Verlag.
7. Danielson GC, Lanczos C (1942) Some improvements in practical Fourier series and their application to X-ray scattering from liquids. J Franklin Inst 233(5):435-52.

   [Crossref][Google Scholar]

8. Winograd S (1980) Arithmetic complexity of computations. SIAM.
9. Duhamel P (1986) Implementation of" Split-radix" FFT algorithms for complex, real, and real-symmetric data. IEEE Trans 34(2):285-95.

   [Crossref][Google Scholar]

10. Good IJ (1958) The interaction algorithm and practical Fourier series J R Stat Soc Series B Stat Methodol 20(2):361-72.

    [Crossref][Google Scholar]

11. Pei D, Salomaa A, Ding C (1996) Chinese remainder theorem: applications in computing, coding, cryptography. World Scientific.
12. McKay S (2010) The secret life of bletchley park: the ww11 codebreaking centre and the men and women who worked there. Aurum.
13. Gannon P (2006) Colossus: bletchley park's last secret. Atlantic Books Ltd.
14. Lavington S (2012)  Alan turing and his contemporaries: building the world's first computers. BCS.

    [Crossref][Google Scholar]

15. Jones K (2022) The regularized fast Hartley transform. : Low-Complexity Parallel Computation of the FHT in One and Multiple Dimensions: Springer.
16. Akl SG (1989) The design and analysis of parallel algorithms. Prentice-Hall, Inc.
17. Maxfield C (2004) The design warrior's guide to FPGAs: devices, tools and flows. Elsevier.
18. Bernhardt C (2019) Quantum computing for everyone. MIT Press.
19. Shor PW (1994) Algorithms for quantum computation: Discrete logarithms and factoring. IEEE FOCS 124-134.

    [Crossref][Google Scholar]

20. Hankerson D, Menezes A (2004) Elliptic curve cryptography. Springer.

    [Google Scholar]

21. Zagorin P (1999) Francis Bacon. Princeton University Press.