Short Communication, J Phys Res Appl Vol: 9 Issue: 1

Macroscopic Quantum-Mechanical Scattering. Coherent Scattering of Neutrinos

Apostol M^*

Department of Theoretical Physics, Institute of Atomic Physics, Magurele- Bucharest MG-6, POBox MG-35, Romania

*Corresponding Author: Apostol M 
Department of Theoretical Physics, Institute of Atomic Physics, Magurele- Bucharest MG-6, POBox MG-35, Romania
E-mail: apoma@theory.nipne.ro

Received date: 09 October, 2023, Manuscript No. JPRA-23-116153;
Editor assigned date: 12 October, 2023, PreQC No. JPRA-23-116153 (PQ);
Reviewed date: 26 October, 2023, QC No. JPRA-23-116153;
Revised date: 17 January, 2025, Manuscript No. JPRA-23-116153 (R);
Published date: 24 January, 2025, DOI: 10.4172/jpra.1000131

Citation: Apostol M (2025) Macroscopic Quantum-Mechanical Scattering. Coherent Scattering of Neutrinos. J Phys Res Appl 9:1.

Abstract

Keywords: Neutrino scattering; Coherent scattering; Macroscopic coherence; Neutrino detection

Introduction

In two papers published in 1985 and 1988 Weber claimed that neutrinos (antineutrinos), from various sources like tritium, nuclear reactors and Sun, could be detected by their coherent scattering by a perfect, stiff, sapphire mono-crystal with a high Debye temperature (mounted on a torsion balance and equilibrated by a lead dummy)[1,2]. The coherent cross-section would be σ=N²σ₀, where N is the number of unit cells in the target and σ₀ is the cross-section of a single unit cell (particle, e.g., atomic nucleus). Such a highly enhanced cross-section ∼N² would give rise to a measurable force upon a torsion balance. Weber’s claims have been criticized both on theoretical and experimental grounds, the main objection being that the form-factor would reduce appreciably the cross-section, and, on the other hand, such a coherence effect is not observed in X, gamma rays or neutron scattering [3-7]. A discussion of the theoretical objections and negative experiments was given by Nicolescu, who presented a positive experiment; indeed, an experiment by Cruceru et al., exists, which confirms Weber’s prediction for solar neutrinos. The problem is still controversial. We show in this paper that a coherent scattering of neutrinos may appear in the conditions formulated by Weber and company, as a consequence of a quantum-mechanical treatment of the crystal as a whole (a macroscopic quantum-mechanical scattering). This is a distinctive condition of the neutrino scattering, which is not fulfilled by other projectiles, with a higher cross-section. The main reason for such a behavior is precisely the extremely small crosssection σ₀ (of the order 10⁻⁴⁴ cm²) of the neutrinos [8-10].

For σ₀=10⁻⁴⁴ cm² and N=10²² (less than 0.1 mol) the coherent crosssection is σ=1 cm². For a neutrino flux density Φ=10¹²/cm² s. The time between two collisions is τ=1/Φσ=10⁻¹² s. On the other hand, an atom in thermal equilibrium at room temperature has a velocity of the order v=10⁴ cm/s. In an elementary act of collision the atom is perturbed from its equilibrium state and receives a momentum of the order p=E/c, on average, where E is the energy of the neutrino projectile (and c=3 × 10¹⁰ cm/s is the speed of light). For E=1MeV the momentum transfer is of the order p=5 × 10⁻¹⁷g cm/s. Consequently, the energy perturbation of the atom is of the order ΔE=p²/M=2.5 × 10⁻¹¹ erg for M=10⁵ m_e, where m_e â? 10⁻²⁷ g is the electron mass (vp=5 × 10⁻¹³ erg << p²/2M). The time needed for this atom to recover its equilibrium is of the order Δt_eq â? ħ/ΔE 4 × 10⁻¹⁷s (where Ä§ â?10⁻²⁷ erg.s is Planck’s constant). We can see that τ >> Δt_eq. It follows that the atoms recover quickly their equilibrium state between two successive collisions, and the incident neutrino beam sees the crystal as a whole. Therefore, we need to adopt a quantum-mechanical treatment for the entire crystal. It is worth noting that if the cross-section increases to, say,

σ₀=10⁻²⁴ cm², as for X-, gamma rays or neutrons, the "collision" time decreases to τ=10⁻³² s, which is much shorter than the equilibrium time Δt_eq, all the other conditions remaining the same. In that case the incident projectile beam sees the crystal as consisting of distinct, independent atoms, such that a coherent scattering (σ=N²σ₀) for the entire crystal is not possible. The particularity of a coherent scattering suffered by neutrinos in the whole crystal resides precisely in their extremely small cross-section σ₀. On the other hand, a single-particle cross-section σ₀=10⁻²⁴ cm² increases considerably the total cross-section, such that we need to reconsider the scattering in this case [11].

Description

Macroscopic quantum-mechanical scattering: Let us assume a macroscopic target consisting of N â?« 1 identical "atoms" (atomic nuclei, molecules, unit cells in a crystal). The interaction with an incident beam of particles can be written as

Where a is the range of the single-particle interaction Ò» (ξ), ξ denotes the internal coordinates of the atoms and ri are the atomic positions. The time between two successive collisions is τ=1/Φσ, where Φ the incident is flux density and σ is the total cross-section. In an elementary act of collision an atom receives a momentum of the order of the momentum p of the incident particle. The atom has a thermal velocity

Where, T is the temperature and M is the mass of the atom. The atomic motion is perturbed by an energy of the order ΔE=p²/M+Ê?p, so it needs a time Δt_eq â?? ħ/ΔE E to recover its equilibrium. Let us asussume

then, the incident particles see the macroscopic target as a whole, and we need to work with the wave function of the whole, macroscopic, target. A perfect mono-crystal suffers two kinds of motion. One kind is the motion of the crystal as a whole, where all the laticial positions of the atoms r⁰_i move by the same distance. The wave function corresponding to this motion is

Where K is the quasi-wave vector of the crystal (quasi-momentum ħK) and

are (orthonormal) wave functions localized on the positions ri. We can see that the wave function ФФ_K has the translational symmetry of the crystal. We call Ф_K a coherent wave function. The other type of motion of the crystal is the thermal motion with atomic displacements

the corresponding wave function is

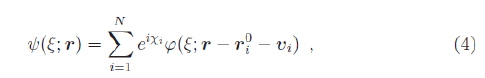
where e^iχi are random phase factors; we call ψ an incoherent wave function. Both these wave functions are normalized to N; they are orthogonal to each other. The wave function of the crystal is

where g is a weight coefficient. This coefficient is proportional to the square root of the relative number of vibration states of the crystal, properly normalized. This relative number of phonon states is proportional to

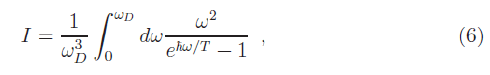
We can see that for high Debye temperatures the main contribution to Ñ°_K comes from the coherent wave function (gâ?ª1), while for low Debye temperatures the main contribution comes from the incoherent field (g→1).

Let us assume a wave function

for an incident particle, and an initial (i) wave function

where V denotes the volume. The normalization to unity of this wave function requires a factor

in the wave fuctions φ, such that the scalar product is

The matrix elements of the interaction between the wave functions Ф_K and ψ are zero. The matrix elements of the interaction between two wave functions Ф_K and Ф_K′ (coherent scattering) lead to the momentum conservation

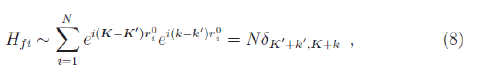
where k′, K′ are the wave vectors of the final state (f). We can see that the difference in momentum of the incident particle is taken by the crystal, which moves as a whole. According to equation (8) the coherent cross-section is

Where σâ?? is the single-particle cross-section. A similar calculation for the incoherent matrix elements (wave functions ψ) leads to

Where

We can see that the difference in momentum of the incident particle is taken by phonons; the incoherent scattering excites phonons. In addition, the incoherent cross-section is proportional to N. For the cross-section we need to average (qv_q)² over the thermal states. The maximum value of this average is of the order T/Mc² s (at room temperature), where c_s is the mean phonon velocity (of the order 10⁶ cm/s). This thermal factor is reminiscent of the Debye-Waller factor (and the diffuse scattering). The total incoherent cross-section can be written as

Where the single-particle cross-section Equation, arising from phonons, is smaller than σ₀ by the thermal factor.

The total cross-section of the crystal is

The incoherent cross-section is extremely small in comparison with the coherent cross-section. For atoms placed randomly (like in amorphous solids, liquids, etc) the coherent wave function Ф_K is absent and the weight coefficient is g=1.

Neutrino scattering

We adopt N â??10²² for the number of unit cells in the sapphire monocrystal (â?? 24 g, density 4 g/cm³) used in Weber’s experiments and other similar experiments (the volume of the unit cell of sapphire is large, â?? 10³Å³). Making use of σâ??=10⁻⁴⁴ cm² we get a coherent crosssection σ_coh â?? 1 cm². For a Debye temperature Θ =10³K the weight factor at room temperature is

The total coherent cross section is σ₀ 0.7 cm². We note that this cross-section is smaller than the cross-sectional area of the crystal. For a flux density Ф=10¹²/cm²· s the collision time is τ=1/Фσ_coh â?? 10⁻¹² s. At room temperature the thermal velocity of an atom is v â?? 10⁴ cm/s. For a neutrino energy E=1 MeV the momentum is p=E/c â?? 5 · 10⁻¹⁷g · cm/s. The perturbation energy is ΔE=p²/M â?? 2.5 × 10⁻¹¹ erg (for an atomic mass M=10⁵ m_e, where m_e is the electron mass); the contribution E=vp â?? 5 × 10⁻¹³ erg is much smaller. The equilibrium time is of the order teq=ħ/ E â?? 4 × 10⁻¹⁷ s. Since τ â?« teq the macroscopic quantum-scattering described above applies.

The force acting upon the target in the forward direction is F=Фσp â?? 3.5 × 10⁻⁵ dyn. This is a measurable force. We note that it is sensitive to the values of the input parameters. For instance, a Debye temperature Θ=100 K leads to a weight coefficient

and a weaker force by a factor â?? 5. Also, for an amorphous solid, although the conditions of a quantum-mechanical scattering may be fulfilled, the force is extremely weak, as a consequence of the very small incoherent cross-section.

For solar neutrinos (E â?? 300 keV) the single-particle cross-section may preserve its value, but the flux density is smaller (Ф â?? 10¹¹/cm² · s). The conditions of a coherent scattering are preserved, but the force may be diminished by a factor â?? 10⁻¹ (â?? 10⁻⁶ dyn). Also, a decrease may appear for tritium neutrinos (E=10keV, Ф â?? 10¹⁴/cm² · s), though a higher σâ?? or a slightly greater number of unit cells N may compensate the decrease (while preserving the conditions of coherent scattering). We note that a large number of atoms in the unit cell, as for a sapphire crystal, may increase the single-particle cross-section σâ??. We conclude that Weber-type experiments could exhibit measurable force acting upon a sapphire crystal.

Other projectiles

Coherence domains: We adopt the value σ₀=10⁻²⁴cm² for other types of projectiles (like X, gamma rays or neutrons). A coherent cross-section would be much larger than the cross-sectional area of the crystal. The crystal responds to this unphysical situation by developing coherence domains. Let us assume that nd uncorrelated domains exist in the crystal, each with Nd unit cells (as a mean size), such that nd=N/ Nd. By a formal analogy with the high-purity crystals we use the fraction f=1/Nd. This fraction varies between f=1/N, when we have only one domain, i.e. the whole target, and f=1, when the whole target is fragmented in "atomic" domains.

The scattering amplitude can be written as

Where

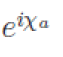
are random phase factors. By averaging the squared scattering amplitude over the phase factors, we get

Such that the cross-section becomes

Where σ_d is the cross-section of a domain. According to this equation, the coherent cross-section σ_coh=σâ??N² is reduced by the coherence domains to

we can see that this formula gives the total coherent cross-section (σ₀N²) for f=1/N and an incoherent cross-section (σ₀N) for f=1. In this latter case σ₀ should be replaced by

(a similar procedure leaves the incoherent cross section arising from phonons unchanged,

In order to have a quantum-mechanical scattering the conditions τÌ? t_^eq and σÌ? A should be satisfied, where A is the cross-sectional area of the target; these conditions lead to

and a number of unit cells Nd=1/f−24 cm² this number is too small for any macroscopic target (N_d<10²A, N=10²²); the domains are not well defined, such that f approaches unity and the scattering tends to an incoherent scattering. We conclude that the quantum-mechanical scattering cannot appear for large single-particle cross sections, like σâ??=10⁻²⁴cm². We note that for neutrinos (σâ??=10⁻⁴⁴cm²) f >10⁻²²/A, Nd<10²²A and we may have one domain in the whole target.

The coherent scattering occurs for neutrinos in a crystal precisely due to the small neutrino cross-section σâ??. The above considerations apply also to a polycrystalline target, where f is limited, in addition, by the size of the crystallites and, consequently, the cross-section is much diminished.

Classical scattering

If in equation (2) is not satisfied (i.e., if τ<σt_eq), the incident particles see the target "atoms" (atomic nuclei, molecules, unit cells) as independent scatters. We call this scattering a classical scattering. We can see that this condition implies low energies. The initial wave function is

(up to wave functions corresponding to the internal degrees of freedom), where k is the wave vector of the incident particle, K is the wave vector of the center of mass, R_c is the position of the center of mass and R=r+R_c. The matrix elements of the interaction given by equation (1),

includes the form-factor

Where k′ is the wave vector of the scattered particle and K′ is the final wave vector of the center of mass. We can see that the total momentum, including the momentum of the center of mass, is conserved. For a crystal

Where g is a reciprocal vector of the lattice. For an amorphous target g=0. It follows that we have diffraction peaks. For the crosssection of a peak we get dσ_g ∼ N²do_g, where the solid angle o_g extends to the range Δ_og â?? N^−2/3(2/dk′)², where d is the mean distance between unit cells (scatterers). It follows σ_g ∼ N^4/3/(dk′)². On the other hand the number of peaks is â?? (dk′)² â?« 1, such that the total cross-section is

where σ₀ is the single-particle cross-section. For one peak σ should be divided by the number of peaks. As it is well known, this crosssection is affected by the Debye-Waller factor and diffuse scattering. According to equation (15) for nd=N/N_d=fN domains the crosssection is

For f=1/N we recover the total cross-section N^4/3σ₀ of one domain, while for f=1 the cross-section reduces to Nσ₀ of an incoherent scattering. The conditions τÌ?=1/ФσÌ? < ð??t_eq to 

which implies N_d=1/f<(A/σ₀N)³ (σÌ?< A). For σ₀=10⁻²⁴ cm² and N=10²² the number of unit cells N^d<10⁶A³ in a domain may indicate well-defined domains for macroscopic targets. The force is bounded from above according to the inequality F<ФAp. The in equations (23) imply ΔE < ħФA, i.e. ΔE<10⁻¹⁵Aerg (Ф=10¹²/cm² · s). Therefore, we may set ΔE=vp and p<ħФ/v A. Consequently, this upper bound is given by (v=10⁴cm/s)

For any reasonably large area A and flux density Ф it is difficult to satisfy these conditions (p < ħФA/v) and to measure such a force in current experimental situations. For higher energies the energy transfer is higher and we need to apply in equations (18); the large crosssection in this case leads to an incoherent scattering.

Conclusion

A quantum-mechanical scattering is identified in certain conditions in macroscopic targets, which may lead to a coherent cross-section in high-purity, stiff mono crystals. This coherent scattering may explain the Weber-type experiments of neutrino detection by using sapphire mono crystals. The coherent-scattering conditions are not fulfilled by other types of projectiles, with higher single-particle cross-sections (like X, gamma or neutrons). In these cases a classical diffraction may occur in crystals, which generates a weak force, at the limit of detection.

Acknowledgment

The author is indebted to the members of the Laboratory of Theoretical Physics at Magurele-Bucharest for many fruitful discussions. This work has been supported by the Scientific Research Agency of the Romanian Government through Grant PN 19060101/2019

Statement

The author declares no conflict of interest.

 

References

1. Weber J (1985) Method for observation of neutrinos and antineutrinos. Phys Rev C Nucl Phys 31: 1468.

   [Crossref] [Google Scholar] [PubMed]

2. Weber J (1988) Apparent observation of abnormally large coherent scattering cross sections using keV and MeV range antineutrinos, and solar neutrinos. Phys Rev D Part Fields 38: 32.

   [Crossref] [Google Scholar] [PubMed]

3. Bertsch GF, Austin SM (1986) Comment on ‘‘Method for observation of neutrinos and antineutrinos’’. Phys Rev C Nucl Phys 34: 361.

   [Crossref] [Google Scholar] [PubMed]

4. Casella RC (1986) On the theory of coherent neutrino scattering from crystals. Il Nuovo Cimento A 94: 42-50.

   [Google Scholar]

5. Ho TH (1986) Comments on the. Method for Observation of Neutrinos and Antineutrinos. Physics Letters B. 168: 295.

   [Crossref] [Google Scholar]

6. Aharonov Y, Avignone III FT, Casher A, Nussinov S (1987) Constraints on anomalous scattering of neutrinos from crystals. Phys Rev Lett 58: 1173.

   [Crossref] [Google Scholar] [PubMed]

7. Lipkin HJ (1987) N dependence of coherent radiation from crystals. Phys Rev Lett 1987 58: 1176.

   [Crossref] [Google Scholar] [PubMed]

8. Franson JD, Jacobs BC (1992) Null result for enhanced neutrino scattering in crystals. Phys Rev A 46: 2235.

   [Crossref] [Google Scholar] [PubMed]

9. Su Y, Heckel BR, Adelberger EG, Gundlach JH, Harris M, et al. (1994) New tests of the universality of free fall. Phys Rev D Part Fields D 50: 3614.

   [Crossref] [Google Scholar] [PubMed]

10. Jun L, Xiao C, Jianguo L, Shuhua F, Fangyu L (1995) Test of abnormally large coherent scattering cross section using solar-neutrino. Chinese Phys Lett 12: 136.

    [Google Scholar]

11. Guo-Qiang F, Shan-Qing Y, Liang-Cheng T, Jun L (2006) Improvement of test of solar neutrino coherent scattering with torsion pendulum. Chinese Phys Lett 23: 2052.

    [Google Scholar]