Review Article, Res J Econ Vol: 1 Issue: 1

Marketing Investment Allocation: A Portfolio Theoretic Model

Subrahmanyam Ganti^*

School of Economics, University of Hyderabad, India

*Corresponding Author : Subrahmanyam Ganti
Visiting Professor, School of Economics, University of Hyderabad, India
Tel: +0891-2840511
E-mail: sganti12@gmail.com

Received: September 27, 2017 Accepted: October 15, 2017 Published: October 22, 2017

Citation: Ganti S (2017) Marketing Investment Allocation: A Portfolio Theoretic Model. Res J Econ 1:1.

Abstract

Keywords: Marketing; Investment; Trade-offs; Customers

Introduction

Marketing is turning simple ideas into strategy. A strategy is a coherent direction that encompasses marketing activities. Creating value beyond its products has been the objective of every company in the 21st century. New products may generate magnificent returns but such returns might stay short-lived because competitors constantly nip at the margins. In a world of mobile talent, open markets and brutal competition, it is increasingly difficult to maintain advantage over competitors through product innovation and customer cocreation. Ideas may be borrowed, but originality in their adaptation alone creates success. In this sense there are at least 16 distinct types of marketing models that cover multidimensional aspects of marketing strategies Hanlon et al. [1]. However, none of these models explores the applicability of the Markowitz’s portfolio allocation model to customer value segments. The present study exactly attempts to do that for the first time.

As a result, some companies have figured out how to outdistance rivals through customer-focused strategies that are virtually “imitation proof” [2]. Therefore, creating customer value through customer-focused strategies constitutes the single largest source of competitive advantage for marketers [3]. But what constitutes value and what is customer value still remain remarkably relevant issues for examination even today. While customer satisfaction with service quality and augmented product with value chain form part of the traditional components of a marketing strategy earlier, the recent perspectives have been on, ‘creating and delivering superior customer value’, ‘customer’s value to the firm’ and ‘customer-perceived value’. Integrating consumer value and customer-relationship value in a conceptual frame-work for value-marketing constitutes the mission of marketing management of a firm today. In fact, customer value constitutes the linchpin of marketing strategy and also co-terminus with organizational change in the 21^st century.

The rest of the study is organized as follows: Section 2 outlines the customer life-time value estimation analytics and highlights the five strategies for the marketing investment allocation to build marketing value. Section 3 outlines the portfolio approach rules to optimal allocation of the investment budget and derives some very interesting results and section 4 presents some concluding remarks and caveat.

Customer-lifetime value analytics

Marketing is the business activity of today and assurance of business tomorrow. Customer delight drives delightful earnings from a marketing strategy. The strategy works as a “pearl finder” (Snaiderbaur et al.) [4]. The ‘Pearl’ is the customer-lifetime value (CLV). Marketing metrics for assessing the customer- life time value is a straight forward method.

The value of a customer to a firm is the expected sum of discounted future earnings from the marketing strategy. For a single customer, with a generated margin of mt at time ‘t’, the discounted cash flow (DCF) approach to perpetuity yields the formula for customerlifetime value (CLV) as

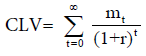                         (1)

Where ‘r’ is the discount rate assumed given. Of course, for convenience sake, this simplified formula is used. To estimate the CLV of the entire customer base, the acquisition rate of new customers and the obsolescence (defection) rate of existing customers need to be incorporated into the model. Suppose the acquisition rate at time ‘o’ is n_o at a cost of ao per customer and a customer retention rate of k_t then the CLV of cohort ‘o’ at time ‘o’ is given by

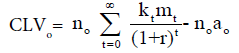(2)

Extending this to the CLV of the i^th cohort at time ‘o’ yields

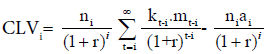                               (3)

In general, the CLV for the s^th cohort at time ‘o’ is given by

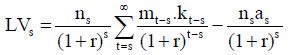                    (4)

Further extending this to the value of a firm’s customer base which is the aggregation of life time value of all cohorts, we get the firm customer base value (FV) as

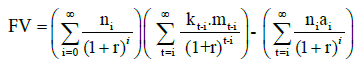         (5)

Customer-value squares

In the above formulation, the new acquisitions of customers could be those referred to by the existing customers. Marketing investment expenditures vary across the existing customers and the newly baptized (acquired) customers called “referrals”. They are treated as investment expenditures because no other costs incurred will have some continuing influence on the referrals for sometime. It is well known that a marketing man is a person who tells you your opinion but not his own. In contrast, a referral dutifully divulges one’s own opinion.

For analysis purposes, Kumar et al. [5] have classified all the customers into those retained and those newly acquired referrals. In terms of customer-lifetime value (CLV) and customer-referral value (CRV) a firm’s customer base can be arranged into a 2 x 2 matrix [5]. All the marketing strategies aim at converting “Affluents” and “Advocates” into “Champions” for maximizing return on the marketing investment. “Misers” are not moved as they may transmit negative and not-very-good messages about the product.

Five great marketing strategies

To err is human; but to really foul business up requires a bad marketing strategy. Great companies fully understand that only a thin line of demarcation runs between marketing relationship and relationship marketing. The only difference between the two is that one can do the latter without marketing. Blind opposition to marketing is as outdated a view as opposition to blind marketing. With a view to gaining first-mover advantage and to build strong network externalities, fast growing firms launch blind marketing strategies, regardless of the cost involved, some times. Of the five strategies to enhance the customer value to the firm [2], the first strategy involves capitalizing on the economies of interactions with the customers into additional returns on the marketing investment. This is in addition to exploiting of the conventional economies of scale, scope and experience into profits. This strategy leads to reducing risks faced by the consumers. Also, the product effectiveness can be maintained without causing faster depreciation of its effectiveness [6]. The second strategy involves maximizing benefits to customers by simplifying the route to those benefits. This route could catapult the company into becoming the link between own customers and the suppliers of complementary products. This not only increases the number of customer “touch points” but also better absorbs the inconveniences and risks associated with the use of the product. This, in turn, enhances customer loyalty and customer value to the firm. The third strategy is meant to gainfully shorten the product life cycle to reach the market much faster. This is said to enhance the turnover component of the return to marketing investment. The fourth strategy is for the company, to “be the nexus” in the supply chain. The purpose is to provide genuine information on related offers so as to enable the customers reduce their search costs. Finally, the fifth strategy works to “form the future” by reducing the lifetime costs for the customers and this protects their investments in the product. All these five strategies work towards not only in acquiring new customers but also in creating the loyalty value for the firm, especially, in the current segment of the consumers. Given that all these strategies confluence in customer relationship management (CRM), the issue of riskreturn trade-off and the optimal allocation of marketing investment becomes the immediate and challenging issue to be examined.

Portfolio model applicability

In this section, we model and develop decision rules for optimal portfolio allocation of marketing investments. For modeling purposes, we assume that the expenditures are broadly allocated between two customer segments – the existing customer segment and a new segment acquired by “referrals”. The two segments are inter-connected through the marketing budget. The two segments are likely to be different in their risk-return relationships. The extant customer segment is likely to be less risky in terms of predictability of its business growth pattern. In contrast, the new “referral” customer segment is considered a relatively more volatile segment regarding its future business returns. This higher volatility of the future returns needs to be compensated in the form of higher return in the riskreturn trade-off parlance. Thus, for purposes of optimal allocation of marketing investment, we can treat the existing customer base as relatively loyal (safer) one and the newer referral segment as the relatively risky one.

Within each segment, the customer base can be further segmented into several markets in terms of customer profitability distribution. The context is amenable for modeling it in a framework of portfolio allocation among ‘n’ customer segments. The portfolio allocation can be done in two stages. In the first stage, the portfolio allocations rules determine the investment allocation within each customer segment. In the second stage, the trade-offs determine the investment allocation between the two broader segments.

Marketing investment allocation

Portfolio theory [7-9] of the financial-asset portfolio allocation, is very much applicable contextually here in the allocation of marketing investment between the two consumer segments. This is done in two stages: First find the optimal mix of highly volatile intra-customer base segments where the risky return to the marketing investment needs to be decided. Next similar optimal mix of the intra-customer base of the relatively less volatile, current customer base needs to be decided. Once the risk-return trade-offs on each of the segments is arrived at, the second stage decision is to allocate the marketing budget between the two customer-base segments. Thus, idiosyncratic risks associated with some customer segments can be diversified away where the returns across the segments are less than perfectly correlated. For instance, the “Misers” segment is one such customer segment. To include this segment in the marketing portfolio results in risk diversification though the segment yields a low return. Section 3.2 elaborates on the analytics of the model and reports some specific interesting cases therein.

The analytics

Let the expected portfolio return R_p be

(1)

Where R₁ and R₂ are the expected returns on segments 1 and 2 and W₁ and W₂ are the shares (weights) of the marketing budget allocated to segments 1 and 2 respectively. Let the variance of the portfolio return be δ²_p, where

(2)

Here, δ₁, δ₂ are the variances, of R₁ and R₂, respectively, and P₁₂ is the correlation coefficient between the returns of the two customer segments. The Mean –Variance theory tells us that the optimization involves minimizing (2) subject to R_p ≤ W₁R₁+W₂R₂. Since W₁+W₂ = 1, we write W₁ and W₂ as equal to W and (1-W) relatively. Hereafter, we denote the correlation coefficient as equal to P. This helps us to rewrite (1) and (2) as

Taking the partial derivative of  w.r.t. W and solving for optimal W* we obtain

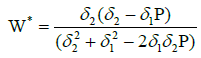
This is the optimal share of the marketing budget to be allocated to the first segment of the customer base. Several interesting special cases can be gleaned from relation (5)

Case 1: If P=1.0, then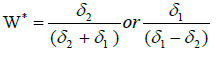

Thus, if the two segments are homogeneous in risk-return tradeoffs, then the optimal share of the budget to be allocated to the segment equals the ratio of standard deviation of one of the returns to the difference between the two standard deviations. In other words, investment in both the segments does not yield any benefits of diversification as the correlation coefficient is unity. So, invest in segment 1 or 2 but not in both.

Case 2: If P=0, then,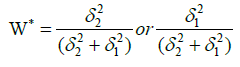

In this case only individual variances of the two segments need to be considered. Budget share is optimal when it equals the ratio of an individual segment variance to the sum of the variances of the two segments. Investing more in that customer segment with low risk (variance) of return would be optimal to achieve minimum risk of the portfolio.

Case 3a: If P= -1.0, then,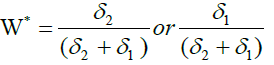

This result suggests that the optimal share of investment in the extant customer segment should equal the ratio of its risk to sum of the risks of both the customer segments.

Case 3b:

In this special case the optimal share in either segment is equal to exactly one half.

Case 4: Supposing that the return to marketing investment in the current customer segment is very stable and almost risk-free. It means implying that δ_p= W δ₂ and R_p = R_f + W (R₂-R_f) or W = R_p-R_f / R₂-R_f. This is a neat result. It suggests that if the current customer segment is the most loyal (means risk-free) one, then the entire marketing budget needs to be invested in the other segment for optimal returns.

Also, 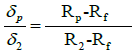this is again a neat result. These two results yield R_p = (R_f + R₂-R_f/δ₂). δ_p In this form, the term (R₂-R_f/δ₂) captures the value of risk as to by how much the expected return of the portfolio should go up for every one unit increase in risk. In other words, the higher is the return chosen for the marketing strategy of the customer segments, the greater is the risk of that strategy. So, to have the most efficient combination between a risky segment and a relatively risk-free segment, the analytics suggest that picking that risky segment with the highest return per unit of risk would be the optimal decision.

Concluding Remarks

Companies today must be interested in both the manner and matter of marketing efforts. Competing companies become increasingly similar in strategies if not in tactics. So they tend to be aggressive in marketing as differences in the way rivals interact with their customers create disparate fortunes. Marketing investment in reducing interaction costs and risks are crucial to these differences as it offers schematic and sustainable way to tap into new sources of customer value. This in turn enhances the portfolio return on the customer-value creating investment.

Optimal budget allocations between market segments leads to very interesting results as explained in cases 1-4 in section 3. Indeed, by implementing the portfolio approach to marketing budget allocations, a company can realize compounding gains in terms of return enhancement for a given risk or minimize risk for a given return. Of course our model takes into account the rates of return from each market segment, variability of the returns and risk neutral behavior of the companies in their market investments [10-12].

Some caveat

A couple of caveat is in order here. It is not true that ‘customer referral value’ is always relevant. One such case is the B2B marketing strategy. Customers in this segment do not, generally, make “referrals” because of the marketing rivalry among them. Individual customers also do not make “referrals” if they do not feel much delight and attachment to the product in a fast moving customer goods market.

Secondly, it is not suggested here that risk minimization is always the dominant objective of a firm. Finally, it is argued that comparative returns from the competing customer segments and their loyalty play a significant role in the portfolio approach to the marketing budget allocations. These models provide marketing strategies with gainfully reliable alternatives to the “rules-of-thumb” and “seat-of-the-pants” decision models.

Epigram-1

Marketing is programmed by an ambitious Mission, so the “Current” can constantly monitor the “Referrals”. It is these “Current” that can confidently check the Erosion And promptly persuade the product “Preferrals”.

Mistakes-2

The mistakes of a beginner are known by everyone but he mistakes of a true winner are known by no one else but him.

References

1. Hanlon A, Chaffey D (2013) Essential Marketing Models: Classic Planning Tools to Inform Strategy, Smart Insights (Marketing Intelligence).
2. Vandenbosch M, Dawar N (2002) Beyond better products: capturing value in customer interactions. Mit Sloan Manage Rev 43: 35.
3. Woodruff RB (1997) Customer value: the next source for competitive advantage. J Acad Market Sci 25: 139-153.
4. Snaiderbaur S (2009) Meeting the Criteria of Delighting Customers. Benedictine college School of Business 1-20.
5. Kumar V, Petersen JA, Leone RP (2007) How valuable is word of mouth? Harvard Bus Rev 85: 139.
6. Brown SP, Gruben WC (1997) Intellectual property rights and product effectiveness. Econ Rev 1:15.
7. Markowitz H (1952) Portfolio selection. J Financ 7: 77-91.
8. Markowitz HM (1959) Portfolio Selection, Efficient Determination of Instruments, Chicago, USA.
9. Sharpe FW (1970) Portfolio Theory and Capital Markets, New York, USA.
10. Goodstein LD, Butz HE (1998) Customer Value: The Linchpin of Organization change. Organ Dyn 27: 21-34.
11. Gupta S, Lehmann DR, Stuart JA (2004) Valuing Customer J Marketing Res 11: 7-18.
12. Payne A, Holt S (2001) Diagnosing Customer Value: Integrating the Value Process and Relationship Marketing. Brit J Manage 12: 159-182.