Research Article, Res J Opt Photonics Vol: 1 Issue: 1

Measuring the Topological Charge of Vortex Beams by the Cross Double-Slit Interference

Hehe Li^1,2*, Jingge Wang^1,2, Miaomiao Tang^1,2 and Xinzhong Li^1,2

¹School of Physics and Engineering, Henan University of Science and Technology, Luoyang, China

²Henan Key Laboratory of Photoelectric Energy Storage Materials and Applications, Luoyang 471023, China

*Corresponding Author : Hehe Li
School of Physics and Engineering, Henan University of Science and Technology, Luoyang, China
Tel: +86 379 6423 1434
E-mail: heheli@haust.edu.cn

Received: November 13, 2017 Accepted: November 14, 2017 Published: November 20, 2017

Citation: Li H, Wang J, Tang M, Li X (2017) Measuring the Topological Charge of Vortex Beams by the Cross Double-Slit Interference. Res J Opt Photonics 1:1.

Abstract

Keywords: Vortex beam; Topological charge; Cross double-slit interference

Introduction

The vortex beams possess the orbital angular momentum which is associated with the azimuthal phase of the vortex beam [1]. The vortex beams have been applied in the different fields of research, such as optical tweezers [2], optical micromachining [3], quantum communication [4,5], as well as the electron vortex beams [6,7] and the electron plasma waves with the orbital angular momentum [8,9].

The topological charge can take integer or fraction value [10], and it is an important parameter of the vortex beams. Thus the measurement of the topological charge is particularly important for the study of the vortex beams. There are two basic methods for measuring the topological charge of the vortex beams, one is the interference patterns, such as the double-slit interference [11,12], the interference of the dynamic angular double slits [13,14], the Mach-Zehnder interferometer [15-17]; the other is the diffraction patterns, such as the triangular aperture diffraction [18-20], the single-slit diffraction [21,22], the annular triangle aperture diffraction [23], the annular aperture diffraction [24], the multipinhole plate [25], the axicon [26] or tilted convex lens [27]. In these two methods, the magnitude and sign of the topological charge can be determined according to the relation between the topological charge and the intensity distribution of the interference or diffraction patterns.

In this paper, we investigate the interference pattern of a vortex beam by cross double-slit theoretically and experimentally. One has known that the diffraction intensity (fringes) of a single-slit depends on the amount of the topological charge [21,22]. The cross double-slit interference pattern can be considered as the superposition of the two single-slit diffraction patterns and its intensity distribution also depends on the topological charge. When the angle between the cross double-slit varies between 0 and 2π, it is found that the topological charge of the vortex beam is equal to the number of interference intensity period. This provides a method for measuring the topological charge of vortex beams. If the phase π/2 is added on one slit of the cross double-slit, the sign of the topological charge can be determined by the advance or delay of the intensity evolution.

Theoretical Formulation

Let us consider that the Fraunhofer diffraction pattern of a vortex beam by a slit. The complex amplitude of a vortex beam (Laguerre-Gaussian beam) can be written in the following simplified form [28].

(1)

where w₀ is the waist width and m is the topological charge of the vortex beam. By means of the Fraunhofer diffraction integral, the diffracted field can be obtained

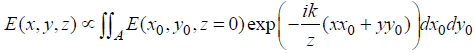(2)

where k=2π/λ is the wave vector, λ is the wavelength and the aperture is a slit which are shown in Figures 1a and 1c, the intensity distribution of the diffracted field are shown in Figures 1b and 1d, which we take the topological charge m=1. The Fraunhofer singleslit diffraction of the vortex beam has been investigated in previous works [21,22] and one obtains that the fringe formation depend on the amount of orbital angular momentum and the slit position in relation to the beam.

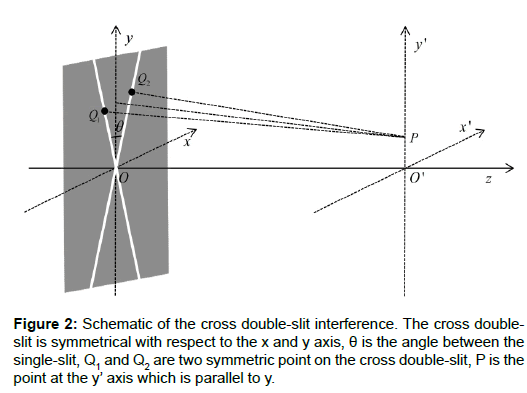
When a vortex beam is incident on a cross double-slit along the z axis just as shown in Figure 2, the angle between the cross doubleslit is θ. One knows that the point P at the y’ axis will experience a constructive or destructive interference pattern which can be considered as the superposition of the two single-slit diffraction patterns, just as shown in Figures 1e and 1f. If the diffracted field of one single-slit is E₁, the other can be written as E₂ exp (-imΔφ), Δφ is the phase difference between Q₁P and Q₂P and has the following form

(3)

where Δs=|Q₁P|-|Q₂P| is the optical path difference between Q₁P and Q₂P. Because the cross double-slit is symmetrical with respect to the y axis which is parallel to y’ axis, the optical path difference Δs=0, so Δφ=mθ. The interference intensity at P can be expressed as

(4)

where I_D=|E₁|²=|E₂|² is the intensity of the single-slit diffraction patterns. We notice that if the angle θ varies between 0 and 2π, there will be a periodic constructive or destructive interference pattern at the point P, the number of intensity periods is determined by the topological charge of the vortex beam.

According to Equation (4), Figure 3 shows the numerical simulation results of the cross double-slit interference pattern for the case of m=1 when the angle θ varies between 0 and 2π. It shows that there is a periodic constructive or destructive interference pattern at the point P and the number of intensity period is equal to the topological charge of the vortex beam (bright→dark→bright). The same result also can be obtained when the topological charge m is changed. For determining the sign of the topological charge, the phase π/2 can be added on one slit of the cross double-slit, Δφ=mθ+π/2, the interference intensity at P can be written as:

(5)

By comparing with the evolution of the interference intensity in Figure 3, there is an advanced or delayed intensity evolution which is determined by the sign of the topological charge. Using the spatial light modulator, the additional phase π/2 can be easily added on one slit of the cross double-slit experimentally.

Experimental Results and Discussion

The experimental setup of the cross double-slit interference of the vortex beams is shown in Figure 4. The vortex beam is generated using computer-generated hologram which is written in the spatial light modulator 1 (SLM1). The cross double-slit is written in the spatial light modulator 2 (SLM2) and we obtain the far-field diffraction pattern at the lens’s focal plane using a CCD. The experimental results for the cross double-slit interference of the vortex beams are shown in Figure 5, which corresponding to the numerical simulation results in Figure 3. In the experimental process, the angle of the cross double-slit varies between 0 and 2π and the topological charge of the vortex beam is m=1. We notice that the number of intensity period is equal to the topological charge of the vortex beam and it is same as the theoretical results obtained above.

Furthermore, using the computer simulation, the additional phase can be implemented on one slit of the cross double-slit and then the sign of the topological charge can be determined by the intensity change (advance or delay) of the interference pattern.

Conclusion

In this paper, we provide a way to measure the topological charge of vortex beams using the interference pattern by cross double-slit in theory and experiment. The cross double-slit interference pattern can be considered as the superposition of the two single-slit diffraction patterns, and its intensity distribution depends on the topological charge. It is shown that the topological charge can be determined by the number of interference intensity period when the angle between the cross double-slit varies between 0 and 2π, the sign of the topological charge can be determined by the advance or delay of the intensity evolution when the phase π/2 is added on one slit of the cross double-slit.

References

1. Allen L, Beijersbergen MW, Spreenw RJC, Woerdman JP (1992) Orbital angular momentum of light and the transformation of  laguerre-gaussian laser modes. Phys Rev A 45: 8185-8189.
2. Grier DG (2003) A revolution in optical manipulation. Nature 424: 810.
3. Ladavac K, Grier DG (2004) Microoptomechanical pumps assembled and driven by holographic optical vortex arrays. Opt Express 12: 1144-1149.
4. Torres JP, Deyanova Y, Torner L, Terriza GM (2003) Preparation of engineered two-photon entangled states for multidimensional quantum information. Phys Rev A 67: 052313.
5. Straupe S, Kulik S (2010) Quantum optics: The quest for higher dimensionality. Nat photonics 4: 585-586.
6. Verbeeck J, Tian H, Schattschneider P (2010) Production and application of electron vortex beams. Nature 467: 301-304.
7. Bliokh KY, Dennis MR, Nori F (2011) Relativistic electron vortex beams: Angular momentum and spin-orbit interaction. Phys Rev Lett 107: 174802.
8. Mendonca JT, Thide B, Then H (2009) Stimulated Raman and brillouin backscattering of collimated beams carrying orbital 125 angular momentum. Phys Rev Lett 102: 185005.
9. Mendonca JT, Ali S, Thide B (2009) Plasmons with orbital angular momentum. Phys Plasmas 16: 112103.
10. Berry MV (2004) Optical vortices evolving from helicoidal integer and fractional phase steps. J Opt A Pure Appl Opt 6: 259-268.
11. Sztul HI, Alfano RR (2006) Double-slit interference with Laguerre-Gaussian beams. Opt Lett 31: 999-1001.
12. Emile O, Emile J (2014) Young’s double-slit interference pattern from a twisted beam. Appl Phys B 117: 487-491.
13. Liu R, Long J, Wang F, Wang Y, Zhang P, et al. (2013) Characterizing the phase profile of a vortex beam with angular-double-slit interference. J Opt 15: 125712.
14. Fu D, Chen D, Liu R, Wang Y, Gao H, et al. (2015) Probing the topological charge of a vortex beam with dynamic angular double slits. Opt Lett 40: 788-791.
15. Leach J, Padgett MJ, Barnett SM, Franke-Arnold S, Courtial J, et al. (2002) Measuring the orbital angular momentum of a single photon. Phys Rev Lett 88: 257901.
16. Leach J, Courtial J, Skeldon K, Barnett SM, Franke-Arnold S, et al. (2004) Interferometric methods to measure orbital and spin or the total angular momentum of a single photon. Phys Rev Lett 92: 013601.
17. Li X, Tai Y, Lv F, Nie Z (2015) Measuring the fractional topological charge of lg beams by using interference intensity analysis. Opt Commun 334: 235-239
18. Hickmann JM, Fonseca EJS, Soares WC, Chavez-Cerda S (2010) Unveiling a truncated optical lattice associated with a triangular aperture using light’s orbital angular momentum. Phys Rev Lett 105: 053904.
19. De Araujo LEE, Anderson ME (2011) Measuring vortex charge with a triangular aperture, Opt Lett 36: 787-789.
20. Anderson ME, Bigman H, De Araujo LEE, Chaloupka JL (2012) Measuring the topological charge of ultra-broadband, optical-vortex beams with a triangular aperture. J Opt Soc Am B 29: 1968-1976.
21. PalGhai D, Senthilkumaran P, Sirohi RS (2009) Single-slit diffraction of an optical beam with phase singularity. Opt Laser Eng 47: 123-126.
22. Ferreira QS, Jesus-Silva A J, Fonseca EJS, Hickmann JM (2011) Fraunhofer diffraction of light with orbital angular momentum by a slit. Opt Lett 36: 3106-3108.
23. Liu Y, Tao H, Pu J, Lv B (2011) Detecting the topological charge of vortex beams using an annular triangle aperture. Opt Laser Technol 43: 1233-1236.
24. Guo C, Lu L, Wang H (2009) Characterizing topological charge of optical vortices by using an annular aperture. Opt Lett 34: 3686-3688.
25. Guo C, Yue S, Wei G (2009) Measuring the orbital angular momentum of optical vortices using a multi-pinhole plate. Appl Phys Lett 94: 231104.
26. Han Y, Zhao G (2011) Measuring the topological charge of optical vortices with an axicon. Opt Lett 36: 2017-2019.
27. Vaity P, Banerji J, Singh RP (2013) Measuring the topological charge of an optical vortex by using a tilted convex lens. Phys Lett A 377: 1154-1156.
28. Palacios DM, Maleev ID, Marathay AS (2003) Spatial correlation singularity of a vortex field. Phys Rev Lett 92: 143905.