Research Article, Res J Opt Photonics Vol: 2 Issue: 1

Multidimensional Modulation in Optical Fibers

Perrone P^*, Betti S and Rutigliano GG

Department of Electronic Engineering, University of Rome “Tor Vergata” Via del Politecnico, Rome, Italy

*Corresponding Author : Perrone P
Department of Electronic Engineering, University of Rome “Tor Vergata” Via del Politecnico, Rome, Italy
Tel: +3313747826
E-mail: pierluigi.perrone@uniroma2.it

Received: November 20, 2017 Accepted: January 01, 2018 Published: January 09, 2018

Citation: Perrone P, Betti S, Rutigliano GG (2018) Multidimensional Modulation in Optical Fibers. Res J Opt Photonics 2:1.

Abstract

Keywords: Polarization modulation; Optical multilevel modulations; Optical fiber; 4-Dimensional modulation format

Introduction

With coherent receivers being increasingly common in optical communications, it is possible a more efficient exploitation of all the resources of the electromagnetic field propagating through the optical link. In fact, coherent systems enable independent use of both quadratures and polarization components of the electromagnetic field for data transmission.

This means that one may use all the 4 Degrees of Freedom (DOFs) of the electromagnetic field to transmit data. The first pioneering work that exploited the possibility of the complete physical representation of the electromagnetic field as a four-dimensional vector was that of Betti et al. [1] with the realization of the 4-Quadrature modulation. Lossless propagation of such a signal vector can then be described by the 4x4 real Jones matrix, similarly to the 2x2 complex Jones matrix (see, e.g., Equation (7) and (8) of Betti et al. [1]), which has four independent parameters (DOFs). These four DOFs cover all the possible physical quantities in electromagnetic wave propagation.

Karlsson [2], completed the concept exposed by Betti et al. [1], by submitting an alternative formalism based on rotations in fourdimensional (4-D) Euclidean space. This formalism describes the presence of two nonphysical extra DOFs. It is clear how the optical coherent systems may well be the first communication systems that are naturally suited for using four–dimensional (4-D) signal constellations [3]. For example, the Dual Polarization-QPSK (DPQPSK) format (whose constellation diagram forms the 16 vertexes of a 4-D cube) used in current Dense Wavelength Division Multiplexing (DWDM) at 100 Gb/s per channel [4].

Meanwhile, as proved from transmission experiments on laboratory based Standard Single Mode Fibers (SSMFs), the current technology is very closer to information theory based capacity limits, estimated at ∼100-200 Tbit/s due to inter-channel nonlinear effects [4].

In recent years, the increasing demand for data rate generated the consciousness of a possible future capacity crunch due to optical fiber nonlinearity [5]. Starting from the above consideration, researchers are trying to explore new fiber types able to support much higher capacities.

In order to build a possible way to reach this fundamental objective, a novel multilevel polarization modulation, applied in twisted fibers in a Local Area Network environment, was first proposed by Perrone et al. [6] and then characterized [7]. This scheme, thanks to the twisting process applied to the optical fiber, exploited the optical birefringence for the creation of physical channels that confined the transmitted symbols during their propagation. A successive contribution, starting from the theory illustrated by Betti et al. [1], proposed a novel multilevel combined polarization-phase modulation in twisted fibers [8]. This scheme was able to reveal the four-dimensional transmitted symbols in the 3-D phase space in which each symbol is constrained around its initial position by the circular birefringence induced in the twisted fiber. Thanks to these innovative modulation schemes, it is possible (i) to decrease the complexity of both the transmitter and the receiver and (ii) to increase the throughput, with the same bandwidth, by exploiting a natural characteristic of the optical fiber such as the birefringence.

In this paper, highlighting the possibility to derive from the original 4-D space several not disjointed 3-D spaces, with a common coordinate between each possible pair among them, we focused on the two 3-D spaces based on two physical quantities of the electromagnetic wave: the polarization and the phase. In particular, our primary contribution consisted on the illustration of how it is possible to design, at the same time, various symmetric constellations in these two 3-D spaces, starting from the original 4-D space. Our novelty is the proposal of a novel multidimensional modulation generated from the union of the constellations in different spaces. As far as we know, this approach has not been proposed before.

The remainder of this paper is organized as follows:

The “Related works” section illustrates the basis for the concepts described in this article.

The “Multidimensional modulations” section details the proposed novel model. Finally, the “Conclusion” section synthesizes the results with a brief glimpse on the possible future developments and applications.

Related works

In order to completely describe and represent all the physical quantities that characterize an electromagnetic wave, it is necessary to adopt the 4-Dimensional point of view. In fact, as introduced by Betti et al. [1], the electromagnetic field propagating in a SSMF can be represented by a four-dimensional vector whose components are the phase and quadrature terms of the two polarization components of the field itself:

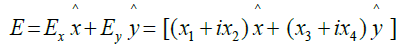(1)

The classical Jones description [9,10], constituted by a 2x2 matrix of complex elements, can be reconducted to an equivalent 4-Dimensional description, by expressing the complex Jones vector as the real 4-vector:

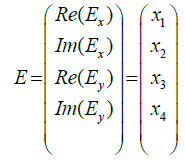(2)

This method provides the complete description of the polarized electromagnetic wave by means of its four real quadrature components. By exploiting this representation of the electromagnetic wave, Betti et al. [1] introduced a new multilevel coherent optical system, called 4-Quadrature modulation, that allows a wider use of the resources of the electromagnetic field for information transmission so to obtain a spectrally efficient modulation format with a limited penalty. The different states of the transmitted field can be viewed as points in a 4-D Euclidean space whose positions can be optimized so to minimize the bit-error probability. It is important to underlines that these four components represent four real physical quantities and not just mathematical encoding. This modulation suffers, during the spatial propagation along the optical fiber, the random rotations imposed by the linear birefringence, predominant in SSMFs, recoverable with a suitable tracking algorithm.

In the 4-D Euclidean space, these rotations present six different DOFs as illustrated by Karlsson [2]. He explained that four is the maximum number of physical quantities available for the electromagnetic field polarization. In particular, he proved that the two extra DOFs in the 4-dimensional description represent nonphysical transformations for travelling photons, since they do not follow the fundamental quantum mechanical boson commutation relations. Therefore, these two extra DOFs are non-physical quantities seen as rotations that can modify the polarization-phase degeneracy of well-known constellations but can also be synthesized with a DSP.

Polarization and phase spaces: Starting from the original 4-D space, the most used derived 3-D space was the polarization space. This space constitutes the environment for the Stokes parameters [11] that represent the State of Polarization (SOP) of the transmitted field. It is possible to derive the Stokes parameters from the four real components of the vector in equation (2) [12]:

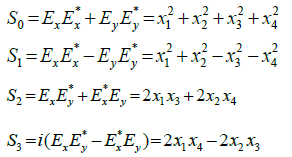(3)

The term S₀ represents the total power of the transmitted field.

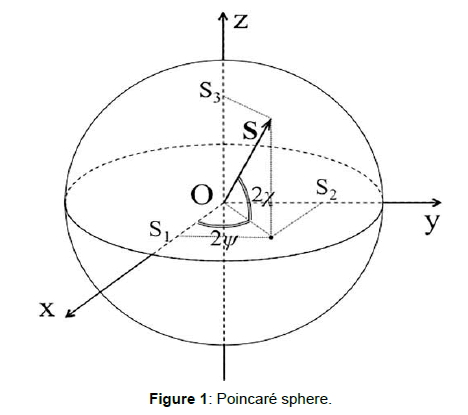
Several optical transmission systems based on polarization modulation have been proposed [13,14]. These systems are based on demodulation of polarization-modulated signals by means of Stokes parameters detection [15]; they exploit the property that each state of the transmitted signal can be represented by a point on the Poincaré sphere [16] (Figure 1). The position of the points that correspond to the transmitted polarization states must be chosen in such a way as to minimize the overall error probability. With these systems, it is possible to obtain a sensitivity improvement. In fact, on the spherical surface, the minimum distance among points representing the transmitted symbols decreases more slowly than on a circle. The SOP of the received optical field can be recognized at the receiver end by simple electronic processing exploiting the property that SOP fluctuations due to fiber birefringence are much slower than the data rate [17].

In the Poincaré sphere, represented in the polarization space, any point identifies a SOP with different longitude (ψ) and latitude (χ). This representation, with each SOP that identifies a different symbol, provides the multilevel polarization modulation.

The second 3-D space that derives from the original 4-D space is the phase space. From the physical point of view, this space and the polarization space form one pair of 3-D spaces with a common coordinate as above cited. Based on the theory described by Born et al. [18], the phase space has three phase parameters, defined in the following way [19]:

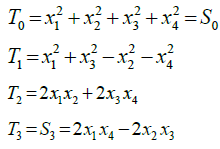(4)

The term T₀, equal to S₀, represents the total power of the transmitted field. The common coordinate to the two 3-D spaces is the third coordinate T₃ that coincides with S₃. It is therefore possible to define, in the phase space, a sphere equivalent to the Poincaré sphere called phase sphere. The two different spheres are related by exchanging x₃ and x₂ in the original 4-D space. The third common coordinate identifies in each sphere the latitude.

Applications in twisted fibers: With the aim to explore and to study the possibility of designing unconventional transmission models, useful to meet the growing data demand, two novel multilevel modulations were proposed by Perrone et al. [6,8]. These models have been designed to be suitable for the optical channel, less complex and more efficient at the same time.

The basic idea is the possibility to improve the single channel throughput of optical fiber by exploiting a natural characteristic of the fiber itself such as the birefringence. This innovative model introduces a new concept: it is more advantageous to design a modulation format that fits the natural characteristics of the channel instead of models that need to correct a posteriori the flaws introduced by the channel.

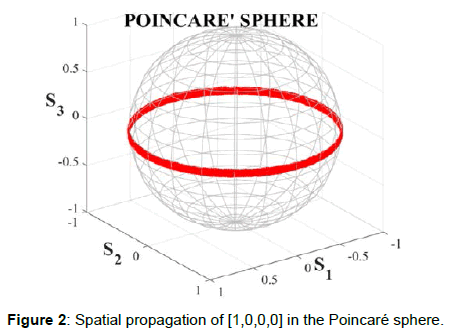
The first model, described by Perrone et al. in [6], introduced a novel multilevel modulation in the polarization space. Classical optical polarization modulations, the most interesting of them are described by Betti et al. [13] and Benedetto et al. [14], suffer the presence of the birefringence, a natural characteristic of optical fiber, which causes random fluctuations of the transmitted SOP during its spatial propagation. Differently from those models, the work by Perrone et al. [6] proposes the use of a suitable twisting process, applied during the manufacturing of the optical fiber, which is able to impose a strong circular birefringence in the core. This circular birefringence, being stronger than the linear birefringence, which causes the above-cited fluctuations and is predominant in SSMFs, creates privileged physical channels (called “bands of polarization”), in which the transmitted symbols are confined latitudinally (the term S3, see equations (3), experiences negligible oscillations around its initial value) during their spatial propagation Figure 2.

Figure 2 shows one of the described physical channels in which a linear SOP, represented by the projection of the point [1,0,0,0] in 4-D space, is confined during its spatial propagation. In this way, there is no longer need of a complex tracking birefringence circuit at the receiver side. This scheme, based on the birefringence models described by Wai et al. [20] and Galtarossa et al. [21], goes beyond the classical concept of symbols belonging to a rigid constellation in the Euclidean space. In fact, it creates a fluid constellation in which the decision regions are defined by the twisting process. The statistical and mathematical reference models described by Perrone et al. [7] strengthen the results exposed by Perrone et al. [6].

Summarizing, this model, which fits very well the LAN environments, presents these fundamental advantages: (i) the increase of the single-channel throughput with the same available bandwidth (by enhancing the twisting process), (ii) the costs reduction due to the low complexity required in transmitters and receivers.

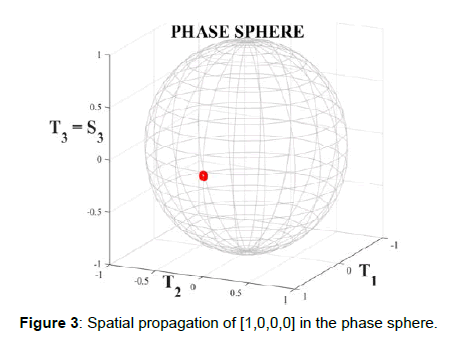
The second model, described by Perrone et al. [8], introduced a novel multilevel modulation in the phase space. This scheme, like the previous, is applied in a LAN environment with the use of a twisted fiber. The proposed model can be seen as a combined polarization-phase multilevel modulation because in the phase space, characterized by the three phase parameters, see equations (4), the third term T₃ coincides with the term S₃ of the polarization space. The twisting process is more advantageous in the phase space with respect to the polarization space. In fact, the induced circular birefringence, besides its effect on the third coordinate (T₃= S₃), is able to confine also the other two coordinates, which identify the longitude, T₁ and T₂. In this way, the transmitted symbol is totally confined, during its spatial propagation along the optical fiber, around its initial position Figure 3. As we can see in Figure 3, the same 4-D point [1,0,0,0] of Figure 2, projected this time in the phase space, experiences negligible oscillations around its initial position for all its three coordinates differently from the point in Figure 2 for which only the term S3 is confined by the twisting process.

This system improves the results reported by Perrone et al. [6], in which the number of physical channels (“bands”), which the twisting process is able to create, limit the number of transmitted symbols (the single channel throughput) because for each “band” of polarization only one symbol can be transmitted. The model by Perrone et al. [8] removes this flaw because in the phase sphere the twisting process is able to confine all the three phase parameters; in this way, it is possible to increase the number of symbols, and consequently the single channel throughput. System performance equals that of classical multilevel polarization modulation [14] with the advantage of a greater throughput and a less complex receiver without the birefringence tracking circuit.

Multidimensional modulations

The systems described by Perrone et al. [6,8] take into account respectively only one 3-D space. The idea underlying this paper is to consider at the same time two different 3-D spaces for the design of a unique constellation belonging to both of them. In order to reach this objective, we start from the original 4-D space in which the electromagnetic wave can be described, in terms of phase and polarization, in the following way [3]:

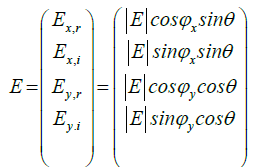(5)

where φ_x and φ_y are the phase terms defined in the interval (-π,π) and the angle Ï´ is usually indicated as the azimuth to describe the orientation in the xy-plane of the linear polarization states. P=|E|² is the optical transmitted power.

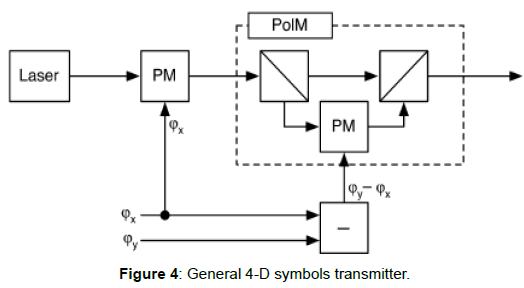
Thanks to this representation, it is possible to build a general transmitter for 4-Dimensional symbols [3] (Figure 4).

This transmitter has a lower optoelectronic hardware complexity, as it requires two Phase Modulators (PMs) and no external Polarization Beam Splitter (PBS). However, one PM is part of a Polarization Modulator (PolM). Other PolM structures and transmitter structures are described by Betti et al. [1,22] and Cusani et al. [23]. A more general PolM was realized in a LiNbO₃ structure [24]. Such a modulator has the possibility of producing any output polarization state for a given specific input polarization state, and its transfer (Jones) matrix can be written as follows:

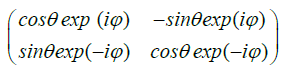(6)

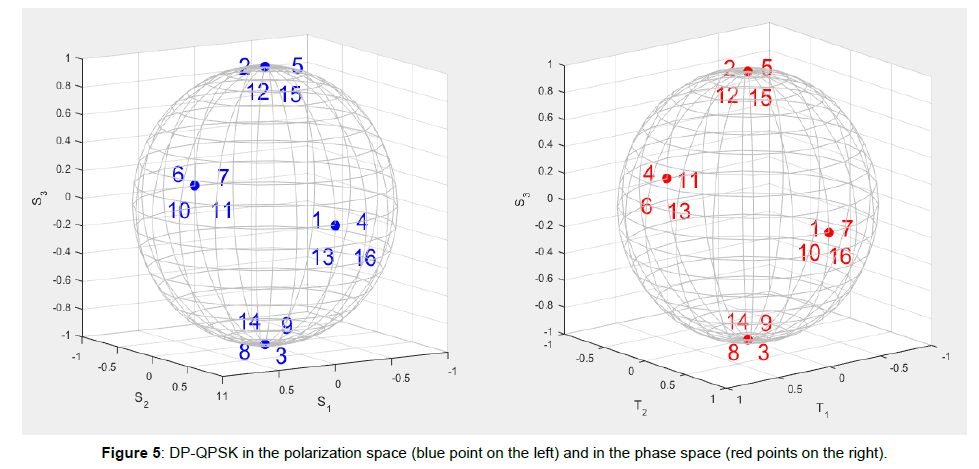
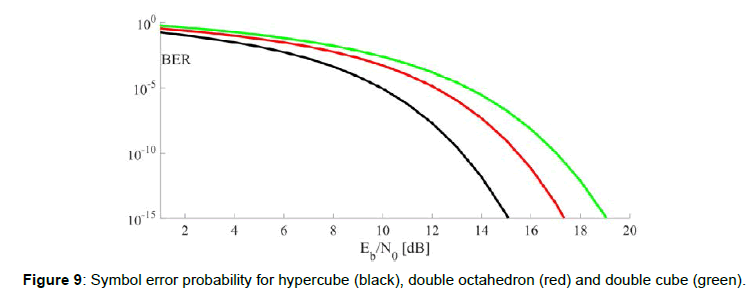
where the term φ=(φ_x-φ_y)/2 is the relative phase between the field vector components. This transmitter is the same used for the DP-QPSK modulation represented in the 4-D space by a hypercube. The hypercube is the best 16 vertexes constellation in the 4-D Euclidean space in terms of distances among the vertexes [25]. The same condition does not hold in the two 3-D spaces of polarization and phase. In these spaces, in fact, the 16 vertexes of the hypercube collapse in four points in each space (Figure 5).

We want instead to design a constellation that could be privileged, in terms of distances among each symbol in both the polarization and phase spaces. In order to analyze this problem, we manipulated equations (3), (4) and (5) obtaining the following results in terms of Stokes and phase parameters:

S₁ = -S₀ cos 2θ

S₂ = S₀ cos (Ï�?_x – Ï�?_y) sin 2θ

S₃ = S₀ sin (φ_y – φ_x) sin 2θ (7)

T₁ = T₀[(sin θ)² cos2φ_x + (cos θ)² cos 2φ_y]

T₂ = T₀[(sin θ)² sin2φ_x + (cos θ)² sin 2φ_y]

T₃ = T₀ sin (φ_y – φ_x) sin 2θ (8)

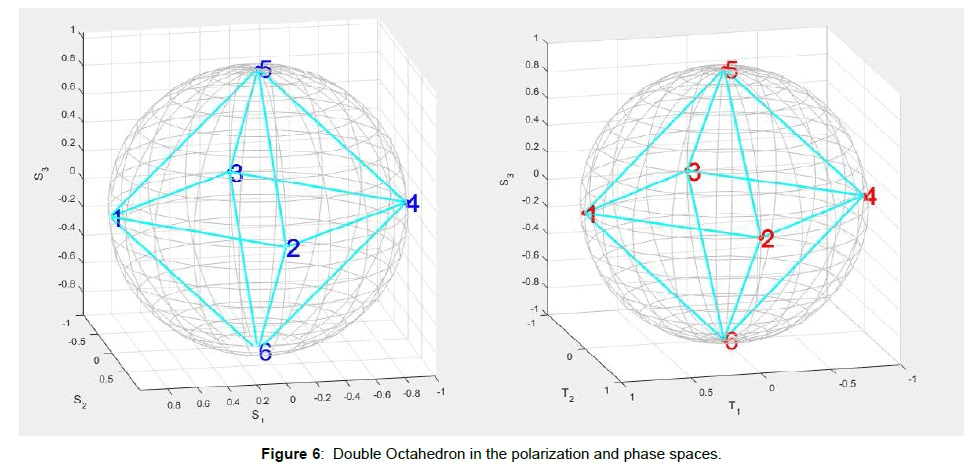
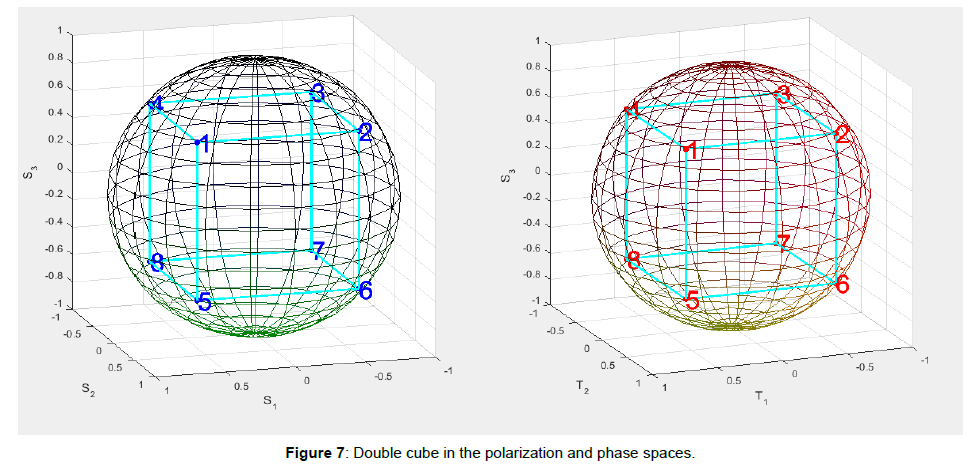
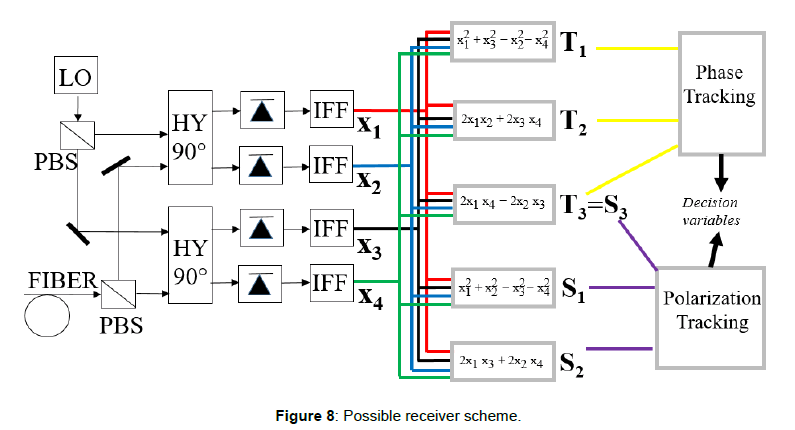
In this way, each term is a function of the polarization and the phase. Thanks to this result, we can design symmetric constellations in both the spaces to form the suitable polyhedron with the best distances among the symbols. For example, Figures 6 and 7 show two possible interesting constellations: the double octahedron and the double cube. Tables 1 and 2 define all the coordinates that characterize these two constellations. In particular, we report the Stokes parameters (S₁,S₂,S₃), the phase parameters (T₁,T₂,T₃) and the coordinates in the 4-Dimensional space (x₁,x₂,x₃,x₄). With this method, it is possible to handle the values of polarization and phase, at the transmitter side Figure 4, in order to design the desired constellation in the related spaces. The constellation in Figure 6 has 18 symbols while that in Figure 7 has 32 symbols. An important consideration is the following: the points placed at the poles of a 3-D space have only a symmetric point in the other space. This is because the latitude is the same (S₃=T₃) and there exists only a point with 90° of latitude. For the other points instead, there is a great possibility of choice because for each point at certain latitude in a 3-D space there exist infinite points at the same latitude in the other space. This type of modulation, differently from those described by Perrone et al. [6,8] can be applied in long haul optical links because it does not use the twisting process. At the receiver end, it will need to recover the phase and the polarization (Figure 8).

The block scheme of the receiver is shown in Figure 8. The received field polarization components are divided by using a PBS; then they are coupled with the corresponding polarization components of the local oscillator by means of two balanced π/2 optical hybrids (HY 90°). The four photodiodes detect the four fields at the output of the hybrids; the obtained electrical signals are proportional to the components of the representative vector of the received field [1]. After detection, there are four identical IF Filters (IFF). This first part of the receiver, which includes the optical and the IF stages, is the same of the receiver described by Betti et al. [1]. The second part of the receiver is the original one. The objective of this section of the receiver is to derive the five independent polarization and phase parameters, starting from the four real components of the received field, as described in equations (3) and (4). The difference with the receiver proposed by Perrone et al. [8] consists, besides the detection of five independent parameters instead of three, in the presence of both the polarization and phase tracking. These tracking mechanisms are necessary because this model is suitable for long-haul optical links that consist of SSMFs (not twisted fibers).

This system presents several advantages. First, it is possible to switch from a multilevel modulation such as the 4-Quadrature in which the symbols are not visible and controllable as they are mapped into a 4-D real Euclidean space to a multidimensional modulation in which the symbols belong, at the same time, to two different 3-D spaces. The Poincaré sphere in the polarization space and the Phase sphere in the phase space constitute the physical containers through which these symbols will be visualized. These two spaces are not disjointed because they are characterized by a common coordinate (S₃=T₃). The multidimensional designed constellation will be the union of two symmetric constellations existing simultaneously in the two 3-D spaces. Therefore, it will be possible to have more independent coordinates (five excluding the power) to exploit. Moreover, the visual representation becomes much more flexible and simple with the same complexity and performance. For example, this feature could be exploited to increase the level of physical security by demodulating the signal in a space rather than another with scrambling operations.

The system performance, calculated with the distance method [26], are illustrated in Figure 9.

Conclusion

In this paper, we proposed an innovative multidimensional modulation for long-haul optical links.

The main result is the proof that, starting from the original 4-D space in which an electromagnetic wave is completely represented, it is possible to derive two physical spaces suitable for hosting the union of two symmetric constellations. In this way, the designed constellation is easily representable.

This method, by suitably handling the polarization and the phase of the electromagnetic wave, permits to design privileged constellations, in terms of distances among the related symbols, not only in the general 4-D space but also in its derived 3-D spaces.

This constitutes an advantage because provides the possibility to switch from one to another 3-D space or to use at the same time both of them.

Possible applications and future developments can be related to physical layer security, with the scrambling of the constellations in the two spaces, and in the improvements of the channel throughput.

References

1. Betti S, Curti F, De Marchis G, Iannone E (1991) A novel multilevel coherent optical system: 4-quadrature signaling. IEEE J Lightw Technol 9: 514-523.
2. Karlsson M (2014) Four-dimensional rotations in coherent optical communications. J Lightw Technol 32: 1246-1257.
3. Agrell E, Karlsson M (2009) Power efficient modulation formats in coherent transmission systems. IEEE J Lightw Technol 27: 5115-5126.
4. Agrell E, Karlsson M, Chraplyvy AR, Richardson DJ, Krummrich PM et al. (2016) Roadmap of optical communications. J Opt 18: 063002.
5. Sillard P (2011) New fibers for ultra-high capacity transport. Opt Fiber Technol 17: 495-502.
6. Perrone P, Betti S, Rutigliano GG (2016) Optical communication system for high-capacity LAN. ‎Microw Opt Technol Lett 58: 389-393.
7. Perrone P, Betti S, Rutigliano GG (2017) Statistical model and performance analysis of a novel multilevel polarization modulation in local 'twisted' fibers. Photonics 4.
8. Perrone P, Betti S, Rutigliano GG (2017) A novel coherent multilevel combined phase and polarization shift keying modulation in twisted fibers. Fiber and Integrated Optics 36: 181-195.
9. Azzam R, Bashara H (1979) Ellipsometry and polarized light. North Holland,Oxford.
10. Ramachandra G, Ramaseshan S (1962) Handbook der physic. Springer, Berlin, Germany.
11. Stokes GG (1852) On the composition and resolution of streams of polarized light from different sources. Trans Cambridge Philos Soc 9: 399-416.
12. Gordon JP and Kogelnik H (2000) PMD fundamentals: Polarization mode dispersion in optical fibers. PNAS 97: 4541-4550.
13. Betti S, Curti F, De Marchis G, Iannone E (1990) Multilevel coherent optical system based on Stokes parameters modulation. IEEE J Lightw Technol 8: 1127-1136.
14. Benedetto S, Poggiolini PT (1994) Multilevel polarization shift keying: optimum receiver structure and performance evaluation. ‎IEEE Trans Commun 42: 1174-1186
15. Betti S, Curti F, Daino B, De Marchis G, Iannone E et al. (1988) A state of polarization and phase-noise independent coherent optical transmission system based on stokes parameters detection. Electron Lett 24: 1460-1461.
16. Poincaré H (1892) Théorie mathematique de la lumieré, 2nd Edtn., Gauthiers-Villars, Paris.
17. Simon A, Ulrich R (1977) Evolution of polarization along a single mode fibre. Appl Phys Lett 31: 517-520.
18. Born M, Wolf E (1959) Electromagnetic theory of propagation, interference and diffraction of light. Principles of optics, Pergamon press, Oxford, New York.
19. Dennis MR (2002) Polarization singularities in paraxial vector fields: morphology and statistics. Opt Commun 213: 201-221.
20. Wai PKA, Menyuk CR (1996) Polarization mode dispersion, decorrelation, and diffusion in optical fibers with randomly varying birefringence. IEEE J Lightw Technol 14: 148-157.
21. Galtarossa A, Palmieri L (2002) Measure of twist-induced circular birefringence in long single-mode fibers: theory and experiments. IEEE J Lightw Technol 20: 1149-1159.
22. Betti S, De Marchis G, Iannone E, Lazzaro P (1991) Homodyne optical coherent systems based on polarization modulation. J Lightw Technol 9: 1314-1320.
23. Cusani R, Iannone E, Salonico A, Todaro M (1992) An efficient multilevel coherent optical system: M-4Q-QAM. J Lightw Technol 6: 777-786.
24. Benedetto S, Djupsjöbacka A, Lagerström B, Paoletti R, Poggiolini P et al. (1994) Multilevel polarization modulation using a specifically designed LiNbO3 device. IEEE Photon Technol Lett 6: 949–951.
25. Rutigliano G, Betti S, Perrone P (2016) Multidimensional Secure Multilevel Polarization Shift Keying. Fiber and Integrated Optics 35: 199-211.
26. Proakis JG (1989) Digital Communications, 2nd Edtn., McGraw-Hill, New York.