Editorial, J Phys Res Appl Vol: 2 Issue: 1

On the Metric Structures and Connection Considerations of Gravitational Field in Finsler Spaces

Stavrinos PC^1*, Ikeda S² and Alexiou M³

¹Department of Mathematics, University of Athens, Ilissia, Athens, Greece

²Ikeda Institute of Applied Geometry, Okayama-City, Japan

³Physics Division, National Technical University of Athens, Athens, Greece

*Corresponding Author : Panayiotis C Stavrinos
Department of Mathematics, University of Athens,Ilissia, Athens, Greece
Tel: (30)2107276416
E-mail: pstavrin@math.uoa.gr

Received: March 12, 2018 Accepted: March 14, 2018 Published: March 20, 2018

Citation: Stavrinos PC, Ikeda S, Alexiou M (2018) On the Metric Structures and Connection Considerations of Gravitational Field in Finsler Spaces. J Phys Res Appl 2:1.

Abstract

Keywords: Metric structures; Nonlinear connections; Finsler Geometry; Fibre bundle; Gravitational field

Introduction

The last ten years the interest in the study of Applications of Finsler geometry to the general relativity, field theory and Cosmology has increased among the scientific community of Theoretical Physicists Different topics of elementary particles of gravitation and cosmology based on the Riemannian geometry are extended in the field Finsler geometry [1-33]. Especially metric models of locally anisotropic form e.g. as Finsler-Randers or Finsler-Randers-like metrics have played an important role in the evolution of structure of the gravitational field,for the Standard Model Extension (SME), Lorentz violation,cosmology [7,18]. Furthermore the concept of osculation between Riemann and Finsler space-time [2] was introduced by Stavrinos and contributed to provide a more connecting form in the study of subjects of general relativity and cosmology in this field, supported in the framework of Riemann-Finsler geometry [5,7].

In the framework of unified description of Finslerian gravitational field Ikeda developed the concept of nonlocalization which is embodied by the internal variable associated with each point of a manifold [34]. Namely, the nonlocalized gravitational field is nonlocalized by attaching the internal variable to each point of the Einstein’s gravitational field. Therefore, the nonlocalized gravitational field has some “non”-Riemannian spatial structure owing to the internal variable. The Finslerian gravitational field is one typical example of the nonlocalized gravitational field, which is nonlocalized by the internal vector y = (yⁱ, i = 1,2,3,4) annexed to each point x = (x^λ ,λ = 1,2,3,4), that is to say the Finslerian gravitational field is the total space of internal and external field for each point-x and fibre-y on the vector bundle.

In a more general consideration the non-locality can be produced attatching to a point p of a base manifold M ^k a scalar or a spinor [35-37]. The concept of nonlocality is introduced to the field theory in order to supply a unified description of elementary particles.

In this paper, after describing the nonlocalized spatial structure of the Finslerian gravitational field, we shall consider some kinds of nonlocalizations of the gravitational field by adopting different internal variables. In particular, we shall consider, in detail, the nonlocalization at the more higher order level (or the more microscopic level) than the Finslerian one. We also introduce the form of nonlinear connection in a FRW-spacetime in the total space of the vector bundle.

Some applications of nonlinear connection are given for different types of Finsler spacetime. As well we present considerations of nonlocalization for a Kawaguchi space in connection with a spinorial structure.

On the Finslerian Gravitational Field

As mentioned in Section 1, the Finslerian gravitational field is nonlocalized by the internal vector y associated with each point x. The vector y constitutes the so-called internal space or the fibre at each point x of the Einstein’s gravitational field, so that the Finslerian gravitational field is regarded as a unified field between the external (x) -field spanned by points {x} of the base manifold and the internal (y) -field spanned by vectors {y} in the internal space. In this consideration the metric tensor g_ij (x,y) is given in each fibre and comes from a differentiable fundamental function F: TM\{0} → R of one-degree homogeneous in the second variable y,

F(x, λy) =λF(x,y), λ>0, y=dx/dt [38,39]. The metric in the fibre has the form 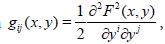which from physical considerations can be degenerate one. From a vector bundle-like view [34], the Finslerian gravitational field is identified with the total space of the vector bundle whose base manifold is the (x) -field and the fibre at the point x is the (y)- field.

In the total space, the following adapted frame is set properly:

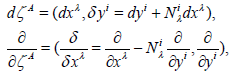(1)

where A=(λ,i)=1,2,3,…,8 and 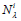denotes the nonlinear connection. A nonlinear connection (N-connection) lives on the total space of the tangent bundle of a manifold M and it can be introduced in the same manner as a linear connection [38,39]. It induces a parallel transport on the base manifold. Locally, a N-connection is defined by a Whitney sum on the tangent space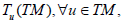

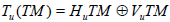where H_uTM denotes the horizontal subbundle and V_uTM the vertical one. Locally the coefficients of N-connection are given by 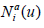with 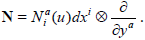The adapted frame is made to be adapted to the direct-sum structure of the metrical structure G_AB of the total space, where

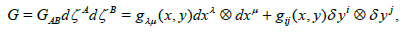(2)

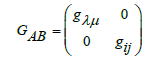
g_λu and g_ij represent the metrics on the base manifold and of fibres. The connection relation is represented by the metrical connection coefficients 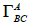, where

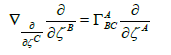
with

(3)

Namely, the covariant derivatives are defined, for example, for an arbitrary vector V(x,y) and have the form

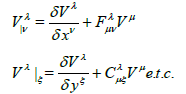(4)

The metrical conditions are considered by g_λμ|_v = 0, g_λμ| = 0 and g_ij|_l=0 and. As is understood from the above, the y-dependence of the Finslerian gravitational field is caused by the nonlocalization with respect to y. In the following, we shall consider some other kinds of nonlocalizations by adopting different kinds of internal variables and generalized or specialized structures of the Finslerian structure mentioned above.

On the Nonlocalization-I

First, if we take another vector z = (z^α: α=1,2,3,4) as the internal variable, besides y, then we can generalize the Finslerian structure by using two nonlinear connections 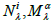as follows:

Adapted frame:

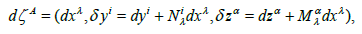(5)

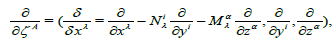
metrical structure:

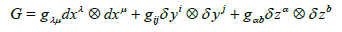(6)

connection relation:

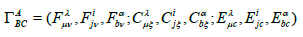(7)

covariant derivatives: 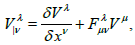(8)

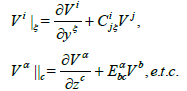
In the above formulas, if y^p= (yⁱ, y⁰) (y⁰is an independent scalar) that belongs to a 5-dimensional space, we can adopt it, instead of yⁱ or z^α, then (5) - (8) are reduced to those formulas for this case, where in (5) - (8), z^α, z^b… are replaced by y⁰ and the indices α, b,… are replaced by 0. This is adjusted to the time-dependent Lagrange geometry with space-time (3+1) dimensions [40-43]. In this case the form of consideration is reduced to the tangent bundle-like one with y⁰ being the time (y⁰ ≡ t) . On the other hand, if we choose only y⁰ as the independent internal variable, then the relations (1) - (4) are reduced to the following formulas:

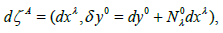
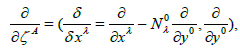(9)

A generalized Finsler - Randers model can be introduced from the metric (2)

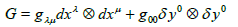(10)

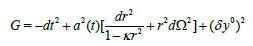
If we apply this study for a cosmological model Friedman- Robertson-Walker (FRW) then the metric of FRW can be extended to the form of the total space.

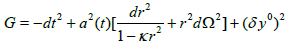(11)

In the above relation we have replaced the first term of the equation (10) with the metric of FRW-model and we have put g₀₀=1. In the case of y⁰ = t₀ = const the rel. (11) is reduced in a spacelike form

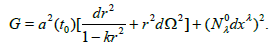
The Christoffel symbols of FRW model are given by

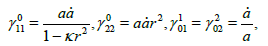
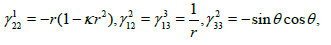(12)

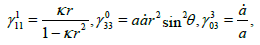
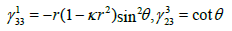
In this case the connection coefficients in the total space can be written as

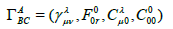
where 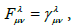with 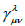Christoffel symbols of FRW metric. In the above mentioned case the covariant derivative of the vector V(x,y) is given by

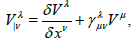
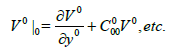(14)

Applications of Non-linear Connection

Some physical meanings of y⁰ and N_a⁰ have already been considered in [4] and for the C⁰₀₀ in cosmology [5].

1. In the classical Kaluza-Klein theory regarding x⁰ as the 5^th coordinate and set g₀₀ = 1 in the rel.(10), then we can find that the nonlinear connection N⁰_λ plays the role of electromagnetic potential. In this case, the torsion tensor defined by 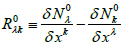represents the electromagnetic field tensor [44].

2. The Finsler-Randers (F-R) metric is given by F(x,y)=(a_ij(x)yⁱy^j)^1/2 + u_iyⁱwith a_ij(x) pseudo-Riemannian metric and u_m represents a weak primordial vector field, where Ç�?u_iÇ�? « 1 The time component u₀ of u_m is incorporated in the geometry of space-time by Cartan’s torsion tensor C⁰₀₀ with the relation 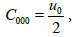[5]. If we substitute this relation to (14) we get

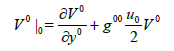
from the last relation we notice that the covariant derivative of V⁰ depends on u₀. A physical interprentation of the non-linear connection for the model of Finsler-Randers space with a type of rotation of angular momenta of galaxies can be given by [1]

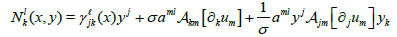(15)

where γⁱ_jk are the Christoffel symbols for the Riemannian spacetime and Akm means antisymmetrization and substruction between the indices k and m. A form of nonlinear connection for the FRWcosmological model in a FR space can be presented by substituting the values of the relation (12) in the relation (15). The Cartan nonlinear connection for a FRW model has the form 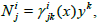where γⁱ_jk take the values from (12). By using Cartan’s nonlinear connection in the relation (15) we get

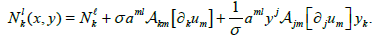(16)

The form of the adapted frame of the rel.(5) becomes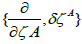

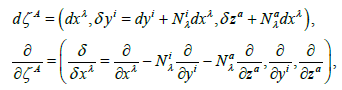(17)

where 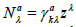are the local coefficients of Cartan nonlinear connection and z^k an internal variable as the yⁱ .

3. A weak nonlinear connection can be given in a F-R model by using a weak Riemannian metric of the form a_ij(x)=n_ij + hij(x), Ç�? h_ij Ç�?=1, where n_ij, represents the Minkowski metric and h_ij(x) a weak perturbation. The corresponding weak nonlinear connection 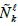for a F-R space-time is written because of (15) as

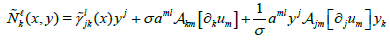(18)

with 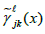the weak Christoffel symbols.

4. In the F-R cosmological model the rotation of a vector u from an axis can â�?�?�?�?^β be given in virtue of a rotation group 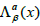. In this case, the nonlinear connection can be written in the form

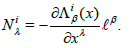
It expresses the variation of the rotation group with respect to the anisotropic axis â�?�?�?�?^β [4]. The rotation group can be used giving a profound geometrical and physical meaning to the concept of nonlinear connection N. The Berwald type form of the nonlinear connection Nⁱ _λ is given by

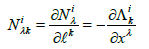
The tensor field 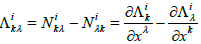denotes the curvature of nonlinear connection and expresses a torsion of variation of the rotation group Λⁱ_k . Non-linear connections have also been considered in the framework of a spinor theory for Finsler spaces [45,46].

On the Nonlocalization-II

Now, we shall consider the nonlocalization at the higher order level than the Finslerian one. First, if another vector Z(= z^α ;α = 1,2,3,4) is taken into account at the one more microscopic level, then the form of consideration is generalized to the second order vector bundlelike form. In this case, the relations (5) - (8) are generalized to the following formulas:

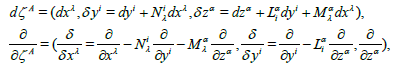(19)

metrical structure: 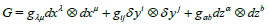(20)

connection relation: 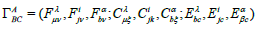(21)

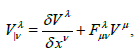
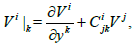
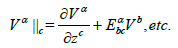(22)

Along this line, we can adopt two or more vectors at the second order or third order or more higher order level, if necessary. The formulas are generalized in the same manner as in (19) - (22) by replacing (x,y,z) with (x,y,z₁,z₂), (x,y,z₁,z₂,z₃),…, where many kinds of nonlinear connections and connection coefficients must be introduced. Similar with the previous consideration in 3 for the metric and the connection of FRW its form can be extended because of nonlocalization (20) - (22) in the framework of a higher order form.

On the Nonlocalization-III

Kawaguchi space and spinor connections

From a more physical viewpoint, if we adopt the more microscopic internal variables other than the vectors such as the spinor,etc. which do not obey the coordinate transformation, then we must take into account the order space-structure higher than the Finslerian space-structure. An analogous but different case has been studied in [28,36,46].

The higher order space (or Kawaguchi space) of order M(=1,2,3,…) is a metrical space in which an arc length along a curve x=x(t) is given by the integral

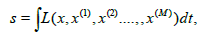(23)

Where L means the fundamental function and 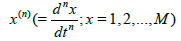plays the role of internal variable in our sense. Of course, this space is regarded as a generalized Riemann or Finsler space nonlocalized by x⁽ⁿ⁾, (x⁽ⁿ⁾(n ≥ 2) is not a vector). The Riemann space is the higher order space of order 0 and the Finsler space is the higher order space of order 1. Therefore, the nonlocalization in this section must be considered within the framework of the higher order space of order M ≥ 2, where the independent variable must be replaced by. (x,y,z≡x⁽ⁿ⁾) (n ≥ 2; y≡x⁽¹⁾)

In this case, δy and δz represent the base connections defined by (for a certain n ≥ 2)

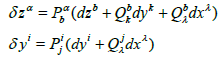(24)

where 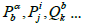are introduced to determine the isomorphisms between the elements of 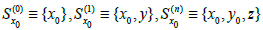and those of 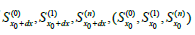and 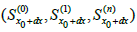being the spaces attached to the generalized line-elements 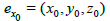and 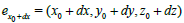respectively. The relation (24) can be formally reduced to the same forms as in (19) under some convenient conditions such as, 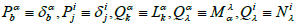but the contents of those quantities are different from each other intrinsically. Those base connections should be determined from a physical viewpoint, by the intrinsic behaviour of y and z .

As to the metrical structure and the connection relation for the case of (x,y,z=x⁽ⁿ⁾) they should be formulated within the framework of the higher order space of order M ≥ 2, which, however, cannot be written in similar and simple forms as in (20) - (22). But, from a physical viewpoint if z = x⁽ⁿ⁾ ,(n >2) is likened to the spinor ψ and (x, ψ) is chosen as the independent variable then (19) - (22) can be reformulated as follows

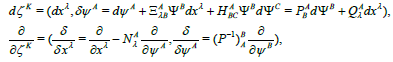(25)

where

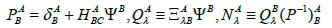
In this case the metric is given by

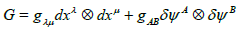(26)

with connections and covariant derivatives

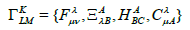(27)

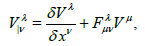
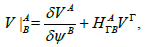(28)

Further, if we take up a nonlocalized spinor field Ï�?�? (x, ψ) then we can define its covariant derivatives in the form

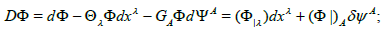(29)

where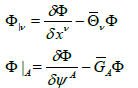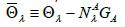

and and 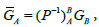A, B represent the spinor indices. Those quantities such as Θ_λ and G_A mean spin affine connections playing the role of spin gauge fields obeying the principle of minimal coupling.

As is understood from the above, our method to nonlocalization can be applied to any internal variable, even if there exist many different kinds of internal variables. One can also extend the content of previous mentioned theories and apply them for connections and metrics on Lorentzian manifolds and Lorentzian metrics on the tangent bundle of a Finsler space-time based on non-linear connections. Furthermore applications of null spacetime can be generalized in the geometry of the total space of a null congruence manifold which were considered in other works for a Lorentzian manifold [45].

This theme will be examined in an upcoming paper.

References

1. Stavrinos P, Diakogiannis F (2004) Finslerian structure of anisotropic gravitational field. Gravitation and Cosmology 10: 269.
2. Stavrinos P (2005) Congruences of fluids in a finslerian anisotropic space-time. Inter J Theor Phys 44: 245.
3. Torrome GR (2006) A Finslerian version of t’Hooft deterministic quantum models. J Math Phys 47: 072101.
4. Stavrinos P, Ikeda S (2006) Connection considerations of gravitational field in finsler spaces. Int J Theor Phys 45: 743.
5. Stavrinos P, Kouretsis A, Stathakopoulos M (2008) Friedmann like- Robertson Walker model in generalized metric spacetime with weak anisotropy. Gen Rel Grav 40: 1403.
6. Skakala J, Visser M (2009) Birefregence in pseudo-Finsler spacetimes. J of Phys: Conf Ser 189.
7. Kouretsis A, Stathakopoulos M, Stavrinos P (2009) General very special relativity. Phys RevD 79: 104011.
8. Kostelecky VA (2011) Riemann-Finsler Geometry and lorentz violating kinematics. Phys Let B 701: 137-143.
9. Kostelecky V, Russell N, Tso R (2012) Bipartite riemann-finsler geometry and lorentz violation. Physics Letters B 716: 470.
10. Torrome R (2012) On Fermat’s principle for causal curves in time oriented Finsler space-times.
11. Skakala J, Visser M (2011) Bi-metric pseudo Finslerian spacetimes. J Geom Phys 61: 1396-1400.
12. Vacaru S (2012) Principles of Einstein-Finsler gravity and perspectives in modern cosmology. Int J of Mod Phys D 21.
13. Voicu N (2011) On the fundamental equations of electromagnetism in Finslerian spacetimes. Prog Electromagn Res 113: 83.
14. Vacaru SI (2012) Modified dispersion relations in horava-lipschitz gravity and finsler brane models. GRG 44: 1015-1042
15. Stavrinos P (2012) Weak gravitational field in finsler-randers space and raychaudhuri equation. Gen Rel Gravit 44: 3029-3045.
16. Chang Z, Wang S (2013) Inflation and Primordial power spectra at anisotropic spacetime inspired by planck’s constraints on isotropy of CMB. Eur Phys JC 73: 2516.
17. Yang S, Lin K (2013) Dynamical effect of electromagnetic wave in spherical symmetrical Finsler spacetime. Int J Theor Phys 52: 3176-3181.
18. Bassilakos S, Stavrinos P (2013) Cosmological equivalence between the finsler-randers spacetime and the DGP gravity model. Phys Rev D 87: 043506.
19. Stavrinos P, Vacaru S (2013) Cyclic and Ecpyrotic Universes in modified Finsler osculating gravity on tangent Lorentz bundle. Classical Quantum Gravity 30: 55012.
20. Silva JEG, Almeida CAS (2014) Kinematics and dynamics in a bi-partite finsler spacetime. Phys Let B 731:74.
21. Xin Li, Chang Z (2014) Exact solution of vacuum field equation in Finsler spacetime. Phys Rev D 90: 064049.
22. Kouretsis A (2014) Cosmic magnetization in curved and lorentz violating space-times. Eur Phys Jour C 74: 2879.
23. Foster A, Pabst C (2015) Finsler pp-waves.
24. Foster J, Lehnert R (2015) Classical-physics applications for b space. Phys Let B 746: 164.
25. Mohseni M (2015) The Raychaudhuri equation for spinning test particles. GRG 47:24.
26. Caponio E, Stancarone G (2015) Standard static Finsler spacetime. Thesis, Cornell University, New York, USA.
27. Singh T, Chaubey R, Singh A (2015) Bounce conditions for FRW models in modified gravity theories. Eur Phys J Plus 130: 31.
28. Vacaru S (2015) Spinor and twistor geometry in einstein gravity and finsler modifications. Adv Appl Clifford Algebr 25: 453-485.
29. Minguzzi E (2015) Raychaudhuri equation and singularity theorems in Finsler spacetimes. Class Quantum Grav 32.
30. Silva JEG, Maluf R, Almeida CAS (2015) A non-linear dynamics for the scalar field in Randers spacetime.
31. Chang Z, Xin L, Wang S (2015) Quadropol-octopole alignment of CMB related to the primordial power spectrum with dipolar modulation in anisotropic spacetime. Chinese Phys C 39.
32. Alexiou M, Stavrinos P, Vacaru S (2016) Nonholonomic ricci flows of riemannian metrics and lagrange-finsler geometry. J Phys Math 7: 1161.
33. Silva JEG (2016) Symmetries and fields in Randers-Finsler spacetime.
34. IkedaS (1980) A differential geometrical consideration on a "nonlocal" field. Rep Math Phys 18:103.
35. Stavrinos P, Ikeda S (1999) Some connections and Variational Principle to the Finslerian scalar tensor theory of Gravitation. Rep Math Phys 44.
36. Vacaru S, Stavrinos P (2002) Spinors and space-time anisotropy. Thesis, Cornell University, New York, USA.
37. Stavrinos P, Manouselis P (1995) Nonlocalized field theory over spinor bundles poincare gravity and yang-mills fields. Rep Math Phys 36 293-306.
38. Miron R, Anastasiei M (1987) The geometry of Lagrange spaces: theory and applications. Kluwer Academic Publishers, Dordrecht, The Netherlands.
39. Vacaru S, Stavrinos P, Gaburov E, Gonta D (2006) Clifford and riemann-finsler structures in geometric mechanics and gravity. Geometry Balkan Press, Bucharest, Romania
40. Anastasiei M, Kawaguchi H (1989) A geometrical theory of time-dependent Lagrangians. Nonlinear connections Tensor NS 48: 272.
41. Ikeda S (1990) Some remarks on the Lagrangian theory of electromagnetism. Tensor N S 49: 204.
42. Kawaguchi A (1932) Die Differential geometrie in der verallgemeinerten Mannigfaltigkeit. Rend Circ Mate Palermo 56: 246.
43. Kawaguchi A (1952) On the theory of non-linear connections I. Tensor NS 2: 123.
44. Ikeda S (1991) On the theory of graviational field in finsler spaces. Tensor NS 50: 256-262.
45. Haesen S, Palomo F, Romero A (2009) Null congruence spacetimes constructed from 3-dimensional Robertson-Walker spaces. Differ Geom Appl 27: 240.
46. Vacaru S, Vicol N (2004) Nonlinear connections and spinor geometry.