Research Article, Res J Opt Photonics Vol: 2 Issue: 2

Single Electron Localization and Tunneling in Weakly Coupled Quantum Dot Array

Filikhin I¹, Karoui A^1*, Mitic V², Maswadeh W¹ and Vlahovic B¹

¹Centers For Research Excellence in Science and Technology, North Carolina Central University, 1801 Fayetteville St. Durham, NC 27707, USA

²University of Nis, Faculty of Electronic Engineering, Medvedeva 14, Nis, Serbia

*Corresponding Author : Karoui A
North Carolina Central University, 1801 Fayetteville St. Durham, NC 27707, USA
Tel: (919)530 6006
E-mail: akaroui@nccu.edu

Received: January 03, 2018 Accepted: January 25, 2018 Published: March 25, 2018

Citation: Filikhin I, Karoui A, Mitic V, Maswadeh W, Vlahovic B (2018) Single Electron Localization and Tunneling in Weakly Coupled Quantum Dot Array. J Opt Photonics 2:2.

Abstract

Keywords: Triple quantum dots; Quantum wells; Single electron states; Localization; Tunneling

Introduction

Due to their unique properties, nanosized semiconductor heterostructures, such as quantum wells (QWs), quantum dots (QDs) and quantum rings are of great interest for the development of highly efficient nano-devices. Also the ability of growing dense and uniform QD assemblies offers new ways for making new generation of quantum devices. However, there are fundamental issues associated with the practical use of QD assemblies. Actually, imperfections in real world QD assemblies impede making efficient QD based devices, and QD assemblies still perform poorly. For instance, QD based third generation solar cells [1-3] have efficiencies much lower than theoretical predictions [4-6] and even worse than QD-less photovoltaic devices. Also, QD based optical and quantum computing devices are still impractical [7-11], despite the varieties of theoretical studies and device design. Nonetheless, the technological implementation of the well-studied InAs/GaAs QDs is under way in various fields. More interestingly, Ge, SiGe, and Si QD arrays have been introduced in large scale optoelectronic integration [12], as well as in third generation solar cells. Also II-VI QDs have been utilized in ultra-bright and pure color display screens [13].

Primary steps for studying large QD assemblies consists in detailed investigation of Double Quantum Dots (DQDs), triple quantum dots (TQDs), QD rings, and QD chains. DQD and TQD are important at the fundamental level, as well as for future technologies. In particular, TQD system has received special attention in connection to electron confinement [14,15] and charge transport [16,17] for it is considered as the building block of two-dimensional quantum arrays, and an essential element for quantum computing. Special emphasis on tunneling, in such systems, stems from its importance for device performance [1]. Hence, we studied electron energy spectra and electron tunneling in InAs/GaAs DQD and TQD quantum systems. We compared the tunneling in these QD systems with chaotic and regular geometries, taking into account recently published results, for instance [18] as evidence of tunneling rate regularization in chaotic systems. Also, we confirmed a strong influence of the system boundaries on the tunneling rate.

Known fabrication technologies always yield, at best, slightly dissymmetric quantum dots and arrays. Dissimilar QDs in the form of truncated disks with atomically flat top surface have been reported in [19]. Such systems induce several convoluted quantum behaviors, for example the drastic change in charge carrier tunneling due to small violation of symmetry, asymmetry induced fine-structure splitting [20], and strong influence of charge transport by chaotic behaviour of such systems [21]. To be noted, chaos and tunneling in the meso- and nano-scale material features have an inalienable relation [22]. These phenomena are highly important for modern and future technologies as mirrored by the relatively long scientific debate [23-28]; for recent review see [29] and references there in.

With regard to charge dynamics in QD arrays, it has been recently demonstrated [30] that spectral distribution of electron localized/ delocalized states and the tunneling in DQDs are highly sensitive to the violation of the geometrical symmetry of QD array and their constituents, see also [31]. The tunneling is a fundamental mechanism of charge transfer in electron confining materials; it is best described by the classical model of wave transmission across the potential barrier of a double well [32,33]. One of the main features of this so called dynamical tunneling [34] is for example the splitting of the energy of the degenerate pairs of levels induced by the coupling between nano-objects. In such quantum system, the wave functions are linear combinations of the electron wave functions bound to the isolated nano-objects [35,36].

In present work, we study single electron localization and tunneling in Triple Quantum Well (TQW). We consider this system as a double QW weakly coupled to a third one, and we study the tunneling in the DQW effected by the third QW. We investigate the effect of coupling on induced states as well as the sensitivity of the tunneling to small symmetry violation.

Theoretical Model

In this work, we consider InAs quantum dots formed within GaAs layers. We focus on observed phenomena in InAs/GaAs QDs that could be approximated as two dimensional quantum wells (QW). The extension to three-dimensional models requires larger computing resources for numerical modelling, however it does not add fundamental insights.

A variety of QDs is modelled [37] based on the kp-perturbation single sub-band effective mass approximation. In these cases, the problem is mathematically formulated by the Schrödinger equation:

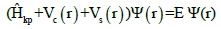(1)

where 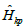is the single band kp-Hamiltonian operator 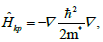m* is the electron effective mass, which depends on the radial position of the electron, thus can be written as m*(r), and Vc(r) is the band gap potential. The Ben-Daniel-Duke boundary conditions [38] are used at the interface of the QW material and the substrate. We use the confinement model proposed in [38] for the conduction band. Both potentials Vc(r) and Vs(r) act inside the QWs. While the potential Vc is attractive, the potential Vs is repulsive. The latter is added to simulate the strain effect in the InAs/GaAs heterostructure. We do not correct the electron mass, for instance, by taking into account the non-parabolic approximation, because of its small effect on this quantum system [29].

Inside the QD the bulk conduction band offset is null, i.e., Vc(r)= 0, while it is equal to Vc outside the QD. The band gap potential for the conduction band is chosen to be Vc(r)= 0.594 eV. The bulk effective masses of InAs and GaAs are m₂^* = 0.067 m₀ and m₂^* = 0.067 m₀, respectively, where m₀ is the free electron mass.

The magnitude of the effective potential Vs(r) that simulates the strain effect is adjusted so to reproduce experimental data for the InAs/ GaAs quantum dots. The adjustment depends mainly on the materials composing the heterojunction, and on the QD topology, to a lesser degree. For example, the magnitude of Vs for the conduction band chosen in [39] is 0.21 eV. This value was obtained in [40] to reproduce the results obtained based on eighth band k.p calculations for InAs/ GaAs QDs. The value of 0.31 eV was obtained from experimental data reported by Lorke et al. [41]

Numerical solution of Equation (1) gives the wave function and energy of a single electron in isolated QW or in pair of QWs (DQW) or in array of QWs. Upon appropriate choice of sizes of QWs, the system demonstrates atom-like electron energy spectrum that encompasses hundreds of confined electron levels.

To describe the tunneling of a single electron in a DQW, we define (for each energy level) a localization parameter σ as follows:

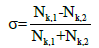
which varies within the range of [-1,1]. N_k,γ is the probability of electron localization in the Ω γ region, hence it can be written as N_k,γ =�?�?Ω _γ |Φ(x,y)|² , where γ =1,2 and Φ_k(x,y) is the electron wave function for k=1,2,...., the energy quantum numbers that constitute the electron spectrum in a DQW.

For the ideal case of QW₁ and QW₂ having the same shape and size, the electron presence in either QW₁(Ω₁) or QW₂(Ω₂) has equal probability. For this state, the electron is delocalized and σ = 0. The cases of σ equal or very close to 1 or -1 correspond to electron localization either in QW₁ or QW₂ .

Results and Discussion

Atom-like system

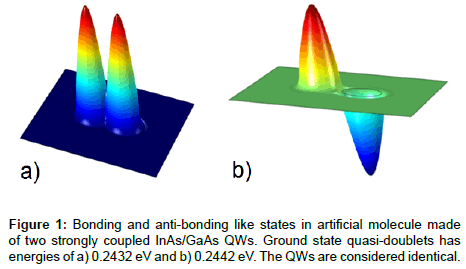
In a double quantum system, the single electron spectrum is composed of a set of symmetric and anti-symmetric state pairs (quasi-doublets). As example, two wave functions of the quasidoublets are presented in Figure 1, for strongly coupled QWs. In that case, the parameter σ is equal to 0 for either of the two quasi-doublet members. These electron states are delocalised. Energy splitting between members of the quasi-doublet is used as the tunneling rate. Akin diatomic molecules, the DQD appears to have two states, each is characterized by an energy level similar to bonding and anti-bonding energy of the molecule. In molecular physics, chemical reactions lead to transition from one quantum state to another, which result in dissociation or association of the constituent atoms. The case of weakly coupled DQW can be obtained from initial state of separated QWs by reduction of inter-dot distance. The localization parameter σ being within the interval -1< σ <1 allows the probability of electron localization on the left and on the right QW to vary and to be eventually different.

Double quantum wells

A pair of adjacent discs acting as QDs are assimilated to be a two dimensional double quantum well (DQW). Ideally symmetric or nearly symmetric quantum wells are important to current study. An example of experimental possibility for highly symmetric , elongationfree QDs was reported [42]. Dynamics of localized and delocalized states along electron spectrum in DQW with dependence on interdot distance was studied [30]. It was shown that tunneling between QWs occurs from high energy levels to the ground state as inter-dot distance consistently decreases. The electron spectrum appears to have three components resulting from: localized states, delocalized states, and states with different probability for localizations in the left and the right sides of the DQW. Noteworthy is the extreme sensitivity of the spectral distribution of the third component to small variations of QW shape, which violate left-right symmetry of the DQW.

This fact can be explained by the dependence of total wave function of “two level” quantum system [32] on the energy difference, ΔE_1,2 between left and right subsystems, considered isolated. One can write electron wave functions of a quasi-doublet (for one dimension system) as a combination of wave functions of isolated QWs (i.e., basis set):

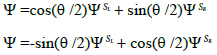(2)

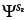where tan(θ)=2W/ΔE_1,2 with 0 ≤ θ ≤ π, W is matrix element of confinement potential of left (respectively, right) QW with wave functions (respectively, ) of isolated QWs. Competition of ΔE₁₂ and W effects defines the type of localization in the system. The wave functions are expressed by the formula 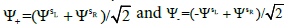for the ideal case of identical QWs, that is when ΔE₁₂=0. Such situation is seen in Figure 1 for delocalized states of a single electron. The localized states appear for isolated QWs when ΔE_1,2 ≠ 0, and W=0. The states with different probability for localizations in the left and the right sides of the DQW appear for the values of ΔE_1,2 and W which provide non-trivial coefficients in the form given in equation (2). Inverse dependence of the coefficient on ΔE_1,2 leads to high sensitivity of the wave function to variation of geometry of the left and right QWs. Due to numerical errors, related to discretization of Equation (1) on a finite coordinate mesh, the ideal situation of identical QWs cannot be realized in the presented numerical modeling. We estimate that the results presented in this paper have numerical error for ΔE_1,2 of about 10^-7eV, considering “identical” QWs.

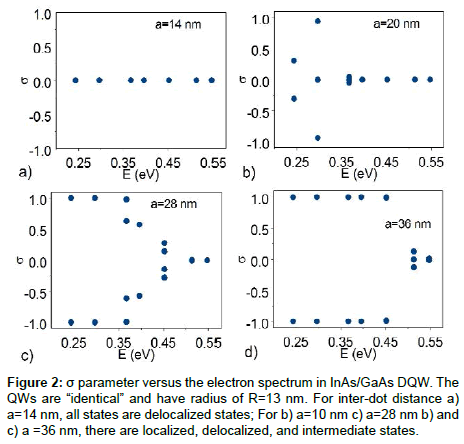
Typical spectral distribution of localized/delocalized states in DQW is shown in Figure 2 through the variation of σ parameter as a function of inter-dot distance. One can see that the σ parameter, as well as the quasi quadruplets and quasi doublets that readily appear in the DQD spectrum, are symmetric about σ = 0 axis. Calculations showed that if the inter-dot distance is less than 10 nm then all electron states are delocalized. However, when the distance is larger than 36 nm, no delocalization occurs and the QWs can be considered as isolated. When the inter-dot distance is between the values 10 nm and 36 nm, there are localized, delocalized and intermediate states in the spectrum. Dynamics of the spectral distribution of localized/ delocalized states can be described as follows: delocalized states consequently appear at the upper levels of the spectrum when the DQW inter-dot distance is decreased from initial value of 36 nm.

Sensitivity to symmetry breaking

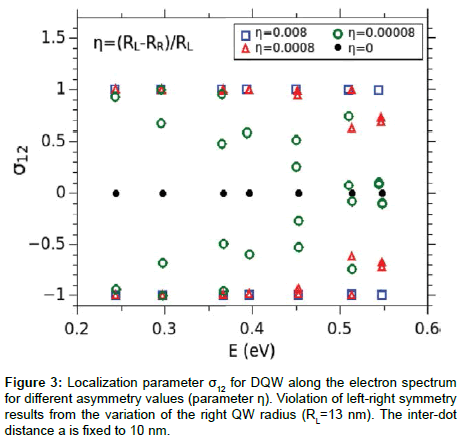
The sensitivity of the tunneling in DQWs to symmetry violation is illustrated in Figure 3, where σ₁₂ parameter (specifically describes the tunneling between QW₁ and QW₂ and characterizes the localization) is shown as a function of the energy of electron confined states for different values of �?�? (asymmetry parameter �?�?= (R_L-R_R)/R_L, where R_L and R_R are the radii of left and right QWs). The spectral distribution for ideally symmetric DQW (�?�? =0) encompasses totally delocalized states. A small symmetry violation (e.g., �?�? = 0.8%) changes the electron localization distribution to completely localized. It can be shown that the sensitivity of the localization parameter varies as 1/ΔE², where ΔE is the energy difference of the same level when considered in isolated left and right QWs. According to this relation, small symmetry violations, when ΔE →0, results in strong variations of electron localization.

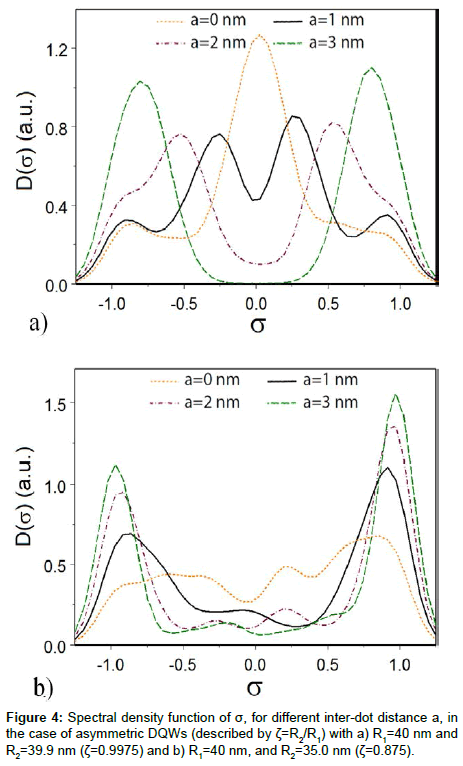
We further demonstrate in Figure 4 (see also [30]) that the spectral density D(σ), which readily shows the distribution of localized/ delocalized states of the DQW, is largely affected by the slightest asymmetry of the DQW configuration. In Figure 4 (a), a small dissymmetry appears, indeed, in the delocalized state distributions for the QW radii ratio ζ= 0.9975, the case of a slightly asymmetric DQW. Electrons are delocalized for most energy levels when interdot distance is zero (QWs are in close contact). This situation quickly changes when the distance increases to 3 nm, where most electron levels become localized. For a stronger asymmetry of DQW, for instance ζ= 0.875. (Shown in Figure 4 (b)), the electron probability is higher in the vicinity of the larger QD (on the right side), independent of the inter-dot distance. In contrast to the previous case, all electron states are mostly localized. For a distance null (when the QWs are in close contact), the distribution turns out chaotic, without any discerned peak.

Generally, violation of the DQW geometrical symmetry changes the inter-dot distance threshold beyond which the tunneling between the dots becomes possible. For identical QWs considered in previous section, a distance of less than 36 nm is required for electron tunneling. This distance is significantly smaller for asymmetric DQWs. One can clearly see in Figure 4 (a) that the distance is about 3 nm for DQW that has an asymmetry of ζ= 0.9975.

Triple Quantum Wells

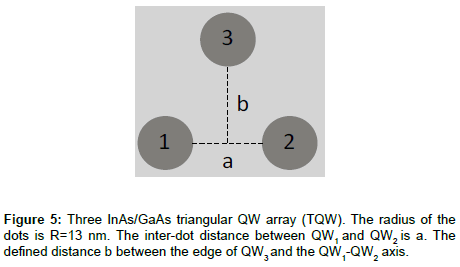
Effect of media: The modification of the tunneling in DQD by a third QD is understood as the effect of media on the electrons. Triple quantum well (TQW) array is considered with various configurations, in particular triangular and linear QW arrays. We focus on two effects, the first is related to adding a third quantum well (QW₃) to the system of two quantum wells (QW₁ and QW₂) and the second is related to small violations of symmetry though changes of QW positions in TQW. We assume a weak coupling of the QWs within the TQW. The changes in the electron localization dynamics over the whole spectrum is studied for a pair of QWs by varying the inter-dot distances within the TQW. Figure 5 shows the TQW geometry and its defining parameters. The QWs are assumed identical. The dot radii were chosen to be R₁=R₂=R₃=13nm. The height b and the distance a between QW₁ and QW₂ have been varied. The distance between QW₁ and QW₃ (which is equal to that between QW₂ and QW₃) is given as

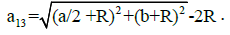
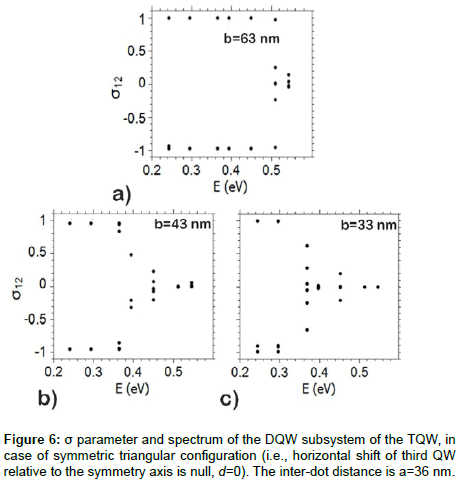
The spectral distribution of delocalized states in DQW and the effect of adding a third QD to form a TQW was modeled. In the TQW, the QWs were arranged in isosceles triangular configuration (see Figure 5). To analyze spectral distribution of localized and delocalized states within the TQW, we selected QW₁ and QW₂ to form a DQW subsystem, and studied the modification of the tunneling and the electron states by QW₃. As seen above, the tunneling in isolated DQW goes consecutively from high energy levels to the ground state when the inter-dot distance is decreased. The behavior of tunneling in DQW, within the TQW, is shown in Figure 6; it appears similar to that in isolated DQW. The spectral distribution of delocalized states in DQW demonstrates that the tunneling increases when the third QW gets closer to the QD pair. The tunneling parameter σ is presented in Figure 6, for three TQD configurations, where the height of the isosceles triangle is decreased from 63, to 43, to 33nm. As the third quantum dot gets closer to the others, significant tunneling occurs for the energy levels less than 0.55, 0.45, and 0.37 eV, as respectively shown in Figure 6 (a-c). Consequently, the part of electron spectrum of delocalized states is decreases.

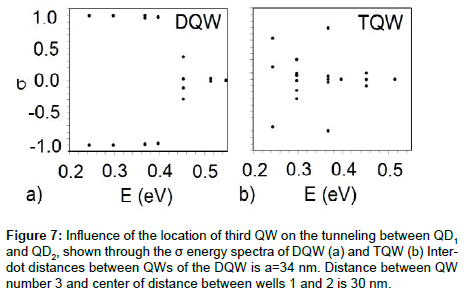
Further effects of the third QW interacting with the DQW is shown in Figure 7, where the spectral distribution of delocalized states in the DQW are compared to that of the same DQW associated with the third QW (i.e., forming a TQW). For the latter, one can see that the number of delocalized states in the spectrum is larger than in the DQW. In addition, the energy for localization-delocalization transition is lower for TQW, i.e., 0.368 eV versus 0.452 eV. Thus, the addition of a QW to the DQW drastically changes tunneling properties of the DQW, and the coupling is enhanced in the DQW.

Asymmetry and tunneling in TQW

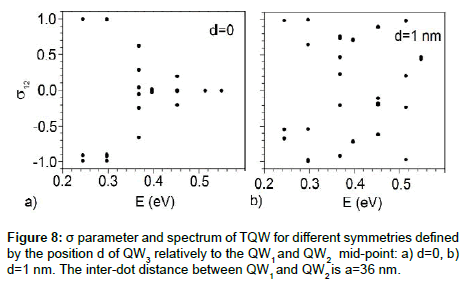
Figure 8 shows the effect of symmetry breaking on the σ parameter describing the tunneling in TQD, where the location of the third QW is modified relative to the mid-point by d, indicated in Figure 10 (b).

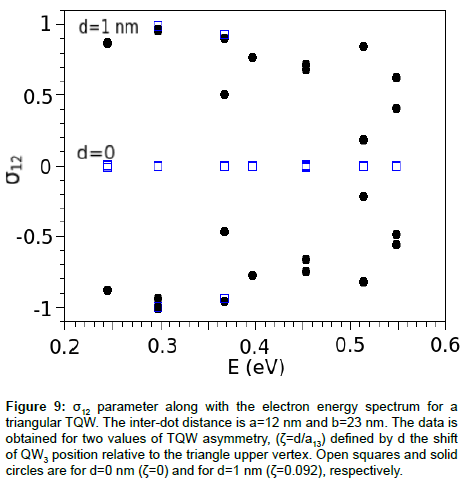
As can be seen in Figure 8, the commonly understood spectral distribution of the localized/delocalized states appears “chaotic”. This infers that the symmetry breaking weakens the coupling between QW pairs and decreases the number of delocalized states. To further demonstrate the effects of symmetry violation, we show in Figure 9, the spectral distribution of the σ parameter for two such cases. The first is the spectrum of totally delocalized states of a DQW; for each level of the spectrum the electron is delocalized. The second corresponds to the situation where the TQW symmetry is violated; this was achieved through shifting the third QW by d=1 nm. One can see that electron is localized for most spectral levels. The effect is strong, though the shift of the third QW is only 9% of the inter-dot distance a₁₃.

To elucidate the effect of topology combined with symmetry violation by QW position within the TQW array, a linear configuration of identical QWs is utilized. The σ₁₂ parameter was calculated for the ground state of an electron in TQW for different values of the asymmetry. The position of third QW relatively to the center of the a₁₂ distance is shown in the inset for d=+/-1 nm. The shift d changes the quantum states from delocalized to localized, where electron is either bound to QW₁ or QW₂.

Results for calculated σ₁₂ are shown in Figure 10 (a), for different values of asymmetry parameter ζ=d/a₁₃, where d is the shift of QW₃ (relative to QW₁ – QW₂ midpoint), and a₁₃ the QW₁ – QW₃ separation distance, see the inset of Figure 10 (b). The electron initial state is localized and σ₁₂ = 0 for all spectral levels. The tunneling to delocalized state is suppressed when ζ is larger than 0.1, as shown in Figure 10 (b). The threshold for delocalization suppression differs for different parts of the spectrum. For low-lying levels, the localized state is reached with smaller values of asymmetry ζ. Comparing the effects of symmetry breaking (Figures 9 and Figure 10), one can conclude that for TQW these effects are not as large as for DQW. Similar result was obtained above for TQW with triangular configuration, shown in Figure 9. The tunneling from delocalized to localized state occurs when the asymmetry is larger than 9%.

Conclusion

We studied the spectral distributions of localized/delocalized states in DQWs and TQWs. The single electron spectra in DQW have shown three parts: localized levels (akin of those of isolated QW) when the electron is in one of QWs, levels with different probability for the electron to be in left or right QW (weakly coupled wells), and delocalized levels when the coupling is strong and the probabilities are equal. We showed that the tunneling in DQW is extremely sensitive to small asymmetrical variations of the QW shapes.

For TQWs, we correlated the tunneling between a pair of QW to the position of third QW (QW₃). The tunneling in the DQW is enhanced as the third QW is added to the system. The influence of QW₃ on the tunneling is interpreted as an “effect of the medium”.

We found that the tunneling is very sensitive to the position of the third QW relative to the pair. In particular, variations of TQW geometry, while violating the symmetry of the system, leads to decreasing the number of localized states of the spectrum. As a result, the tunneling between the QWs significantly decreased. Such sensitivity is technologically important for future quantum devices as well as next generation photovoltaic cells.

Acknowledgements

This work is supported by award DHS-16-ST-062-001 from the Dept. of Homeland Security, award HRD-0833184 from NSF, and award D01_ W911SR-14-2-0001-0002 from MSRDC/ECBC-DOD.

References

1. Conibeer G (2007) Third-generation photovoltaics. Mater Today 10: 42-50.
2. Nychyporuk T, Lemiti M (2011) Silicon-based third generation photovoltaics,solar cells–silicon,wafer-based technologies, (4th edtn), InTech, Rijeka, Croatia.
3. Karoui A, Kechiantz A (2012) Quantum mechanics design of two photon processes based solar cells, some applications of quantum mechanics, InTech, Rijeka, Croatia.
4. Luque A, Marti A, Stanley C (2012) Understanding intermediate-band solar cells. Nat Photonics 6: 146-152.
5. Beard MC, Luther JM, Nozik AJ (2014) The promise and challenge of nanostructured solar cells. Nat Nanotechnol 9: 951-954.
6. Nozik AJ, Beard MC, Luther JM, Law M, Ellingson RJ, et al. (2010) Semiconductor quantum dots and quantum dot arrays and applications of multiple exciton generation to third-generation photovoltaic solar cells. Chem Rev 110: 6873-6890.
7. Markov IL (2014) Limits on fundamental limits to computation. Nature 5: 147-154.
8. Zhirnov VV, Cavin RK, Hutchby JA, Bourianoff GI (2003) Limits to binary logic switch scaling - a gedanken model. Proc IEEE 91: 1934-1939.
9. Aaronson S, Shi Y (2004) Quantum lower bounds for the collision and the element distinctness problems. J ACM 51: 595-605.
10. Nielsen MA, Chuang IL (2011) Quantum computation and quantum information,Cambridge Univ Press, New York, United States.
11. Jain R, Ji Z, Upadhyay S, Watrous J (2010) QIP = PSPACE. Commun ACM 53: 102-109.
12. Murty BS, Shankar P, Raj B, Rath BB, Murday J (2013) Applications of nanomaterials, Textbook of Nanoscience and Nanotechnology, Springer, Berlin.
13. Chigrinov VG (2014) Liquid crystal photonics, Nova Science Publishers, New York, United States.
14. Hawrylak P, Korkusinski M (2005) Voltage-controlled coded qubit based on electron spin. Solid State Commun 136: 508-512.
15. He Z, Lu T (2012) Transport through a triple quantum dot system: formation of resonance band and its application as a spin filter. Phys Let A 376: 2501-2505.
16. Gaudreau L, Sachrajda AS, Studenikin S, Kam A, Delgado F et al. (2009) Coherent transport through a ring of three quantum dots. Phys Rev B 80: 075415.
17. Taranko R, Parafiniuk P (2010) Electron transport through the triple quantum dot. Physica E 43: 302-307.
18. Rogge MC, Haug RJ (2008) Two-path transport measurements on a triple quantum dot. Phys Rev B 77: 193306.
19. Gaan S, He G, Feenstra RM, Walker J, Towe E (2010) Size, shape, composition, and electronic properties of InAs/GaAs quantum dots by scanning tunneling microscopy and spectroscopy. J Appl Phys 108: 114315.
20. Amloy S, Chen YT, Karlsson KF, Chen KH, Hsu HC et al. (2011) Polarization-resolved fine-structure splitting of zero-dimensional InxGa1−xN excitons. Phys Rev B 83: 201307.
21. Ponomarenko LA, Scheidin F, Katsnelson MI, Yang R, Hill EW et al. (2008) Chaotic Dirac billiard in graphene quantum dots. Science 320: 356-358.
22. Nakamura K, Harayama T (2004) Quantum chaos and quantum dots, Oxford University Press, Oxford, United Kingdom.
23. Baranger HU, Stone AD (1989) Quenching of the Hall resistance in ballistic microstructures: A collimation effect. Phys Rev Lett 63: 414-417.
24. Whitney RS, Schomerus H, Kopp M (2009) Semiclassical transport in nearly symmetric quantum dots. I. Symmetry breaking in the dot. Phys Rev E 80: 056209.
25. Whitney RS, Marconcini P, Macucci M (2009) Huge conductance peak caused by symmetry in double quantum dots. Phys Rev Lett 102: 186802.
26. Nazmitdinov RG, Sim HS, Schomerus H, Rotter I (2002) Shot noise and transport in small quantum cavities with large openings. Phys Rev B 66: 241302.
27. Filikhin I, Matinyan S, Schmid BK, Vlahovic B (2010) Electronic and level statistics properties of Si/SiO2 quantum dots. Physica E 42: 1979-1983.
28. Filikhin I, Matinyan SG, Vlahovic B (2011) Phys Lett A 375: 620-623.
29. Filikhin I, Matinyan SG, Vlahovic B (2012) Quantum mechanics of semiconductor quantum dots and rings, Fingerprints in the Optical and Transport Properties of Quantum Dots, InTech, Rijeka, Croatia.
30. Filikhin I, Matinyan SG, Vlahovic B (2015) Electronic structure of quantum dots and rings. RITS 3: 1-22.
31. Bleibaum O, Belitz D (2004) Weak localization of electrons in an external electric field. Phys Rev B 69: 075119.
32. Tannoudji CC, Diu B, Laloe F (1977) Quantum mechanics, Wiley, Hoboken, New Jersey, United States.
33. Bastard G (1988) Wave mechanics applied to semiconductor heterostructures, Halsted Press, New York, USA.
34. Davis MJ, Heller E (1981) Quantum dynamical tunneling in bound states. J Chem Phys 75: 246-254.
35. Rotter I, Sadreev AF (2005) Avoided level crossings, diabolic points, and branch points in the complex plane in an open double quantum dot. Phys Rev E 71: 036227.
36. Ryu JW, Lee SY, Kim SW (2009) Coupled nonidentical microdisks: avoided crossing of energy levels and unidirectional far-field emission. Phys Rev A 79: 053858.
37. Filikhin I, Suslov VM, Vlahovic B, (2006) Modeling of InAs��?GaAs quantum ring capacitance spectroscopy in the nonparabolic approximation. Phys Rev B 73: 205332.
38. Daniel DJB, Duke CB (1966) Space-Charge Effects on Electron Tunneling. Phys Rev 152: 683-693
39. Filikhin I, Suslov VM, Wu M, Vlahovic B (2009) InGaAs/GaAs quantum dots within an effective approach. Physica E 41: 1358-1363.
40. Schliwa A,Winkelnkemper M, Bimberg D (2007) Impact of size, shape, and composition on piezoelectric effects and electronic properties of In(Ga)As��?GaAs quantum dots. Phys Rev B 76: 205324.
41. Lorke A, Luyken RJ, Govorov AO, Kotthaus JP (2000) Spectroscopy of nanoscopic semiconductor rings. Phys Rev Lett 84: 2223-2226.
42. Ha N, Liu X, Mano T, Kuroda T, Mitsuishi K, et al. (2014) Droplet epitaxial growth of highly symmetric quantum dots emitting at telecommunication wavelengths on InP(111)A. Appl Phys Lett 104: 143106.