Research Article, Vegetos Vol: 29 Issue: 3
Spatial Distribution Behaviour of Thrips in Important Cucurbitaceous Vegetable Crops
| Sardana HR*, Bhat MN, Chaudhary H, Sureja AK, Sharma K, and Mobin Ahmad | |
| ICAR-National Research Centre for Integrated Pest Management, New Delhi 110012, India | |
| Corresponding author : Sardana HR
Principal Scientist (Entomology), National Centre for Integrated Pest Management, Pusa Campus, New Delhi-12, India Tel: +91 9968384033 E-mail: hrsardana@rediffmail.com |
|
| Received: July 21, 2016 Accepted: August 08, 2016 Published: August 16, 2016 | |
| Citation: Sardana HR, Bhat MN, Chaudhary H, Sureja AK, Sharma K, et al. (2016) Spatial Distribution Behaviour of Thrips in Important Cucurbitaceous Vegetable Crops. Vegetos 29:3. doi: 10.5958/2229-4473.2016.00078.1 |
Abstract
Spatial Distribution Behaviour of Thrips in Important Cucurbitaceous Vegetable Crops
The individuals of a species of insects distribute themselves in their habitat with a characteristic pattern. The study of distribution pattern is of considerable ecological significance. Field sampling of an insect population without sound ecological basis can lead to erroneous estimation and conclusions. Control of the pest can be enhanced by the determining its spatial distribution and developing a sampling procedure for estimating its population..
Keywords: Spatial distribution; Field sampling; Thrips, Cucurbits
Keywords |
|
| Spatial distribution; Field sampling; Thrips, Cucurbits | |
Introduction |
|
| The distribution pattern provides information about the behaviour of population and also can be used for measuring the size of population [1]. Thus the adequate knowledge of distribution of insect population gives an insight to formulate pest management strategies. The melon thrips, Thrips palmi Karny are one of the key pests of cucurbitaceous vegetable crops in India. Over the last 10- 15 years Thrips palmi has rapidly become a major pest of cucurbits. Thrips feed gregariously on leaves, stems, flowers and fruits causing severe injury to cucurbits. It has a wide host range and is also cause of virus transmission. So far the research work on Thrips palmi has been restricted to its biology, incidence, feeding behaviour, varietal susceptibility and control [2-4]. No detailed information is available on its spatial distribution. In the present paper, efforts have been made to study the distribution pattern of thrips in major cucurbitaceous vegetable crops at various time intervals. | |
Materials and Methods |
|
| The unprotected cucurbitaceous crops of pumpkin, muskmelon and bottle gourd raised 2014 at the experimental farm of Indian Agricultural research Institute, New Delhi were divided each into eight uniform strata based on Harcourt [5]. Absolute counts of thrips (nymphs and adults) on one inflorescence per plant on five randomly selected plants in each stratum were recorded for each crop. Four such observations at weekly interval were recorded for pumpkin while three observations were recorded for muskmelon and bottle gourd each during May-June. | |
| Spatial distribution | |
| The procedure outlined by Southwood [6] was followed for determining the spatial distribution pattern. Three dispersion indices viz; variance to mean ratio, aggregation index (K) and mean crowding [7] were computed. Lloyd’s index of patchiness, which is the ratio of mean crowding (x*) to mean density (x) was calculated for each set of observation. The mean crowding was obtained [6] as: | |
 |
|
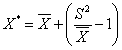| Where, x is the thrips mean density per inflorescence per plant and S2 is the variance. Lloyd’s index equals unity in a random distribution but is greater and smaller than unity in contagious and regular distribution, respectively. | |
| The aggregation index, K, was computed as: | |
 |
|
| After determining the distribution pattern from dispersion parameters, the data were fitted to a negative binomial and Poisson distributions and goodness of fit tested using chi-square (χ2) statistics. | |
| To study the distribution further, Iwao’s [8] patchiness regression, which gives a linear relationship between mean crowding (x*) and mean density (x) over a range of different densities was fitted, | |
 |
|
| Where α is a constant and β the slope. The intercept, the index of basic contagion, indicates whether individual insects are dispersed in colonies and β, the coefficient of density contagiousness indicates whether the colonies were dispersed contagiously. Thus when a single individual is the basic component, α = 0, and value greater or less than 0 indicates a positive or negative association between the individuals. When β is less, equal to or greater than unity, it describes a uniform, random or aggregated distribution of basic components or colonies, respectively. Taylor’s power law [9], which gives a relation between variance and mean, | |
| S2= axb | |
| Where, a is a constant depending upon experimental conditions, b is the coefficient of contagion, was also fitted to the data to further study the aggregation pattern. | |
| To identify the cause of aggregation, the mean clump size (λ) was calculated using the Arbous and Kerrich [10] formula: | |
 |
|
| Where λ is the number of individuals in aggregation for the probability level attached to v (v = function with a chi-square) distribution with 2k degrees of freedom at probability level of 0.50. | |
| Sample size | |
| The optimum sample number (n) of plants for a reasonably accurate estimation of the density of thrips based on the distribution pattern, was also worked out, using Iwao’s formula [11], | |
 |
|
| Where D is the standard error of mean. | |
| Finally to find the appropriate transformation to normalize the data or to make the variance independent of mean, ten sets of data on thrips count were transformed by log (x+1), log (x+k/2), log{log(x+2)} [12],Sinh-1√ (β – 1/ α + 1) x [13], x 1 – b/2 [9] and √x+1. The means and variances were computed and correlation (r) between the variance and mean values worked out for each transformation and compared with (r) of untransformed data. In normalized data, the variance is independent of mean as shown by the correlation coefficient (r) [14]. | |
Results and Discussion |
|
| The results on the spatial dispersion pattern of thrips in three cucurbitaceous crops viz pumpkin, muskmelon and bottle gourd are summarized in Table 1. The mean population of thrips (nymphs & adults) per inflorescence per plant ranged from 2.83 to 5.13. The mean population of thrips was marginally higher in bottle gourd than pumpkin and musk melon. However, the variance exceeded the mean on all dates of observations in the three cucurbits and hence the variance to mean ratio, the simplest method of showing the distribution pattern [9,15], was invariably greater than unity for three gourds viz., pumpkin, muskmelon and bottle gourd. Likewise, the index of mean crowding exceeded the mean density and thereby the Lloyd’s index of patchiness was always greater than unity thereby corroborating the aggregation pattern of thrips (Table 1). This implied that the distribution pattern of thrips was of a contagious type indicating a tendency for aggregation in the spp. The values of the coefficient of dispersion, K, which measures the degree of aggregation, was less than eight in most cases, suggesting a high degree of aggregation [9]. | |
 |
Table 1: Different parameters for spatial distribution of thrips in pumpkin, muskmelon and bottle gourd. |
| On most of the occasions, the negative binomial distribution based on chi square (χ2) values was found to give a better fit of probability to the data sets than the Poisson distribution (Table 1). This further confirmed the clumping pattern of the thrips distribution. | |
To get an insight into the type of aggregation involved i.e. whether it was an aggregation of insects in colonies or whether it was an aggregation of colonies, Iwao’s [8] patchiness regression was fitted, based on the linear relationship between mean crowding and mean density, over a range of different densities  and yielded α = 0.3103 and β = 1.1620. Here, (α) the index of basic contagious, indicates whether individual insects are dispersed in colonies and (β) the coefficient of density contagiousness indicates whether the colonies are dispersed contagiously. When a single individual is the basic component, then α = 0, and greater or less than zero value of (α) indicates a positive or negative association between individuals. When (β) is less than, equal to or greater then unity, it describes a uniform, random or aggregated distribution of the basic component or colonies, respectively. In this study, the two values obtained suggested that the thrips were distributed singly (one insect per colony) but that colonies were aggregated. The data further explained the aggregation pattern of the colonies, in term of negative binomial distribution, of about equal and fixed mean size [8]. The Taylor power law equation yielded a slope (b) value of 1.6289 indicating a clumped distribution of thrips. |
|
| For the population described by the negative binomial distribution, according to Arbous and Kerrich [9], the causes of clumping may be due to either active aggregation by the insect or some heterogeneity of the environment. These workers observed that if λ was less than 2, the distribution was due to environmental heterogeneity while λ values greater than 2 indicated that environment and insect behavior were working together. In our study, the mean clump size (λ) of aggregation was greater than 2 in all the sets of observations. Thus it may be inferred that the clumping of thrips could be due to behavior of females tending to deposit eggs in close proximity in the leaf veins & flowers and to environmental variation mainly caused by the emergence of top leaves which are the also the preferred sites for ovipositing and feeding of the thrips along with inflorescence. In cucurbits field, the females deposit eggs in leaves and flowers. Soon after hatching, the larvae start feeding on succulent leaves and growing tips and among the petals and developing ovary gregariously. This probably explains why in the field, the thrips population is observed in aggregation pattern. | |
| A mean sample size of 44 plants was found to be optimum and appeared to be quite reliable for estimating the population of thrips in cucurbits fields (Table 2) as it was based on the dispersion behaviour of thrips. This may be adopted depending upon time, manpower, convenience and type of study. Southwood [9] suggested that a small sample size representing 2 - 3% of plant population is reasonably good for survey and control studies. However for life table studies etc. a large sample size is required. | |
|
Table 2: Average plant sample size based on Iwao’s (1977) formula for thrips, Thrips palmi on cucurbitaceous crops. |
As the dispersion pattern of Thrips palmi on cucurbits is over dispersed, the need for a suitable transformation to normalize the data before an analysis of variance was felt. Six transformations were used and the mean, variance and their correlation were computed (Table 3). The correlation coefficient for untransformed data was significantly high showing the dependence of variance on the mean. Of the six transformations, three, viz; log (x+1), log [log(x + 2)] and x1-b/2 stabilized the variance. The other transformations viz. log(x + k/2) ,  and  showed dependence of variance on the mean and were not suitable for normalizing the population of thrips. |
|
|
Table 3: Suitability of different transformations for sampling thrips population on cucurbits. |
| The present investigations form a basis for future studies of Thrips palmi on cucurbits crops. Any pest infesting the inflorescence has a direct bearing on yield loss. Therefore, precision estimates of population and sampling decisions within the limits of time and man power are essential. Spatial distribution is unique to a species in relation to its environment, knowledge of which together with the optimum sample size and a suitable transformation will provide the correct approach in field studies leading to management of Thrips palmi in cucurbits. | |
References |
|
|
|