Research Article, Res J Opt Photonics Vol: 2 Issue: 1

Supercontinuum Generation Using Microstructured Optical Fibers

Ferreira MFS^*

Institute of Nanostructures, Nanomodelling and Nanofabrication, Department of Physics, University of Aveiro, 3810-193 Aveiro, Portugal

*Corresponding Author : Ferreira MFS
Institute of Nanostructures, Nanomodelling and Nanofabrication, Department of Physics, University of Aveiro, 3810-193 Aveiro, Portugal
Tel: +351 23 4370356
E-mail: mfernando@ua.pt

Received: November 23, 2017 Accepted: January 01, 2018 Published: January 08, 2018

Citation: Ferreira MFS (2018) Supercontinuum Generation Using Microstructured Optical Fibers. Res J Opt Photonics 2:1.

Abstract

Keywords: Optical fibers; Supercontinuum generation; Raman scattering

Introduction

A number of third order nonlinear processes can occur when high-power light is launched into the optical fibers [1]. These can grow to appreciable magnitudes over the long lengths available in fibers, even though the nonlinear index of the silica glass is very small (n₂ = 2.35×10^-20 m²/W) at 1550 nm [2]).

Fiber nonlinearities fall into two general categories [1]. The first category arises from modulation of the refractive index of silica by intensity changes in the signal (Kerr effect). This gives rise to nonlinearities such as self-phase modulation (SPM) [3], crossphase modulation (XPM) [4], four-wave mixing (FWM) [5], and modulation instability (MI). The second category of nonlinearities corresponds to stimulated scattering processes, such as stimulated Brillouin scattering (SBS) [6] and stimulated Raman scattering (SRS) [7], which are interactions between optical signals and acoustic or molecular vibrations in the fiber, respectively.

A rather interesting nonlinear phenomenon which can be observed in optical fibers is the supercontinuum generation (SCG), which corresponds to an extremely wide spectrum, achieved by an optical pulse along its propagation [8]. It results generally from the synergy between several fundamental nonlinear processes, such as SPM, XPM, SRS, MI, and FWM [1]. The spectral locations and powers of the pumps, as well as the nonlinear and dispersive characteristics of the fiber determine the relative importance and the interaction between these nonlinear processes. A supercontinuum source can find applications in the area of bio-medical optics, where it allows the improvement of longitudinal resolution in optical coherence tomography (OCT) by more than an order of magnitude [9]; in optical frequency metrology [10]; in all kinds of spectroscopy, and as multiwavelength source in the telecommunications area [11].

The fiber nonlinearity is commonly characterized by the nonlinear parameter λ (defined in the next section), which in standard single-mode silica fibers has a typical value of λ ≈ 1.3W-1/km [12]. Such value is too small for some applications requiring highly efficient nonlinear processes, namely for optical signal processing. An improved performance has resulted from the use of microstructured optical fibres (MOFs) [13,14]. MOFs with a small core dimension and a cladding with a large air-fill fraction allow for extremely tight mode confinement, i.e., small effective mode area, and hence, a higher value of γ. Besides, the large refractive index difference between silica and air critically cause a strong waveguide contribution to the overall group-velocity dispersion (GVD) of the guided mode [15]. As a consequence, these structures can provide anomalous group-velocity dispersion and hence conditions for soliton formation at shorter wavelengths than is possible with conventional fibres [16].

Fiber Non-linearity and Dispersion

The fiber nonlinearity is commonly characterized by the nonlinear parameter γ, which is given by (1)

(1)

where λ is the light wavelength, n₂ is the nonlinear-index coefficient of the fiber core and A_eff is the effective mode area, given by:

(2)

F(x,y) representing the spatial distribution of the fiber mode.

Equation (1) shows that, for a fixed wavelength, since n₂ is determined by the material from which the fiber is made, the most practical way of increasing the nonlinear parameter γ is to reduce the effective mode area A_eff. However, the nonlinear parameter γ can also be enhanced using the dopant dependence of the nonlinear refractive index n₂. It has been shown that n₂ increases by doping the bulk glass with GeO₂ [17]. On the other hand, n₂ decreases in the case of an F-doped bulk glass.

Fiber dispersion

The mode-propagation constant β(ω) is related with the refractive index n(ω) in the form

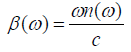(3)

Mathematically, the effects of fiber dispersion are accounted for by expanding β(ω) in a Taylor series about the carrier frequency ω₀ at which the pulse spectrum is centered:

(4)

where

(5)

The group velocity dispersion (GVD) is characterized by the parameter β₂

(6)

where V_g=c/n_g and n_g=n+ω(dn/dω) represent the group velocity and the group refractive index, respectively. In practice, the GVD is often characterized by another parameter, D, given by

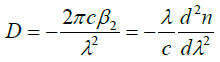(7)

The parameter D gives the delay of arrival time in ps unit for two wavelength components separated by 1 nm over a distance of 1 km. In the case of fused silica, D=0 at λ=λ_ZD=1.276 μm, which is referred to as the silica zero-dispersion wavelength. The parameter D becomes negative (normal GVD) at shorter wavelengths and positive (anomalous GVD) at longer wavelengths.

The overall GVD of a guided mode in an optical fiber depends not only on the material dispersion, but also on the waveguide dispersion [1]. The last contribution becomes especially important in the case of fibers using a large difference in refractive index between the core and cladding materials. Besides affecting the dispersion characteristics, increasing such refractive index difference provides also an enhancement of the nonlinear parameter of the fiber, as discussed previously.

Microstructured optical fibers

Microstructured optical fibers (MOFs) represent a new class of optical fibers that are characterized by the fact that the silica cladding presents an array of embedded air holes. They are also referred as photonic crystal fibers (PCFs), since they were first realized in 1996 in the form of a photonic crystal cladding with a periodic array of air holes [14].

Microstructured fibers can be divided in two main types. One class of fibers, first proposed in 1999 [18], have a central region containing air. Such fibers are usually called hollow-core MOFs and the light propagating in them is confined to the core by the photonic bandgap effect. The nonlinear effects are strongly reduced and the dispersion becomes negligible in this kind of MOFs. A nonlinear coefficient =0.023 W^-1/km was reported recently for a hollow core fiber [19]. However, the nonlinear effects in this type of MOFs can be greatly enhanced if air is replaced with a suitable gas or liquid [20].

The second type of microstructured fibers has a solid core, in which the light is guided due to total internal reflection, since the core has a higher refractive index than the cladding. A solid core MOF with an hexagonal pattern of holes is represented in Figure 1 has two main structural parameters: the hair-hole diameter d and the holeto- hole spacing ∧. In such fibers the periodic nature of air holes in the cladding is not important as long as they provide an effective reduction of its refractive index below that of the silica core [21,22]. This helps to concentrate the mode field in a very small area, which is particularly the case in MOFs with and large air-filling fractions. The tapered fiber considered above can be used to model the behavior of the fundamental mode of air-silica microstructured optical fibers with a high air-filling fraction in their cladding [23].

Figure 2a shows the spatial mode distribution for a microstructured fiber with a hexagonal pattern of holes of diameter d = 0.5μm, spaced by ∧ = 10 μm, considering a wavelength λ=1.55 μm. Figure 2b shows the normalized effective mode area against the normalized wavelength for different hole-pitch ratios. We observe that increasing the hole-pitch ratio the effective area is reduced. Consequently, the nonlinear parameter is increased, as given by Equation (1).

In the case of microstructured fibers and to take into account of the different proportions of light in glass and air, the nonlinear coefficient λ must be redefined as follows [24]:

(8)

In Equation (11) is the nonlinear refractive index of material i (2.9×10^-23 m²W^-1 for air, 2.6×10^-20 m²W^-1 for silica), is the effective area for the light in material i, and is the effective nonlinear index for fiber, with a core area A_core. A nonlinear coefficient λ= 240 W^-1 /km at 850 nm was measured for a solid-core MF with a core diameter of 1μm [14].

A peak power of P₀=5kW launched into a silica MOF with a nonlinear coefficient λ=240W^-1/km provides a nonlinear length L_NL=(λP₀)^-1<1mm. For dispersion values in the range -400<β2<400ps²/ km and pulse durations T₀=300fs, we have a dispersion length . Considering also typical values of fiber loss (α~1-100dB/km), we conclude that both the effective fiber length Leff = (1-exp(-αL)) and the dispersion length L_D are much longer than the nonlinear length L_NL, which means that strong nonlinear effects will be readily observable in solid-core MOFs.

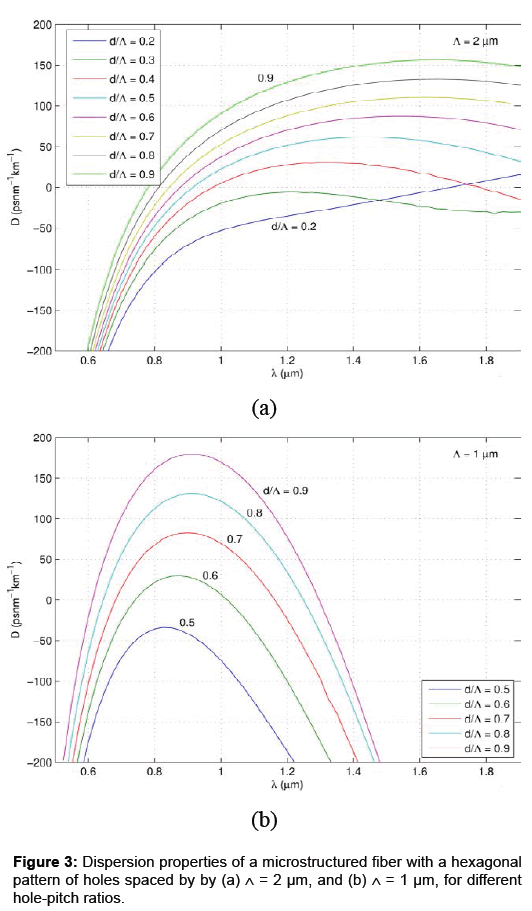
The microstructured cladding offers greatly enhanced design flexibility and can manipulate the dispersion characteristics by controlling structural parameters such as the hair-hole diameter d and the hole-to-hole spacing Λ [25]. In fact, the dispersive properties of MOFs are quite sensitive to these parameters and can be tailored by changing appropriately each of them. Figure 3 shows the dispersion characteristics of a microstructured fiber with a hexagonal pattern of holes spaced by (a) ∧=2 μm, and (b) ∧=1 μm, for different hole-pitch ratios.

In solid-core MOF, as the holes get larger, the core becomes more and more isolated, until it resembles an isolated strand of silica glass. The core diameter of a MOF is given by D_core = 2∧-d. MOFs with larger cores exhibit semi-infinite anomalous dispersion above the ZDW. By decreasing the core size, the ZDW tends to be shifted to a shorter wavelength, leading to the anomalous dispersion at near infrared and visible wavelengths. When the core size is decreased further, a second ZDW arises in the longer wavelength side, such that the GVD is anomalous in the spectral window between the two ZDWs and normal outside it. This situation can be seen in some cases of Figure 3a, 3b. Submicron-diameter MOF cores have been fabricated using a conventional tapering process [26].

Modelling of the Supercontinuum

Modelling the supercontinuum generation can be realized considering a generalized NLSE that includes higher-order dispersion effects, as well as intrapulse Raman scattering. Such equation can be written as (1).

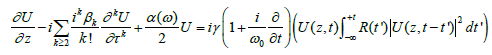(9)

where U(z,t) is the electric field envelope, ω₀ is the center frequency, β_k are the dispersion coefficients at the center frequency, α(ω) is the frequency-dependent fiber loss, and λ is the nonlinear parameter.

The nonlinear response function R(t) in Equation (9) can be written as

(10)

where the δ function represents the instantaneous electron response (responsible for the K_err effect), h(t) represents the delayed ionic response (responsible for the Raman scattering) and f_R is the fractional contribution of the delayed Raman response to the nonlinear polarization, in which a value 0.18 f_R = is often assumed [27]. It is common to approximate h(t) in the form [28,29]

(11)

where τ₁ =12.2 fs and τ₂ = 32 fs. More accurate forms of the response function h(t) have also recently been investigated [30].

Equation (9) can be used to describe the propagation of femtosecond pulses in optical fibers, in both the normal and anomalous dispersion regimes. When such pulses have enough power, their spectra undergo extreme broadening. In the anomalous dispersion regime, this process is mainly influenced by the phenomenon of soliton fission, which occurs whenever a higher-order soliton is affected by third- or higher-order dispersion. The soliton order N is given by [1,28]

(12)

where is the dispersion distance and L_NL=1/λP₀ is the nonlinear length.

In the presence of higher-order dispersion, an Nth-order soliton gives origin to N fundamental solitons whose widths and peak powers are given by [31]

(13)

(14)

where k = 1 to Ñ, where Ñ is the integer closest to N when N is not an integer. Soliton fission occurs generally after propagation distance L_fiss ∼ L_D/N, at which the injected higher-order soliton attains its maximum bandwidth. The fission distance L_fiss is a particularly significant parameter in the context higher-order soliton effect compression [32,33]

Besides higher-order dispersion, another main effect affecting the dynamics of a higher-order soliton fission is the intrapulse Raman scattering (IRS). This phenomenon leads to a continuous downshift of the soliton carrier frequency, an effect known as the soliton selffrequency shift (SSFS) [34]. Such effect was observed for the first time by Mitschke and Mollenauer in 1986 [35]. The origin of SSFS can be understood by noting that for ultrashort solitons the pulse spectrum becomes so broad that the high-frequency components of the pulse can transfer energy through Raman amplification to the lowfrequency components of the same pulse. Such an energy transfer appears as a red shift of the soliton spectrum, with shift increasing with distance.

The rate of frequency shift per propagation length is given by [1]

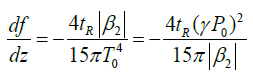(15)

where is the Raman parameter andis the soliton peak power. Since the SSFS effect is proportional to (λP₀)², it will be enhanced if short pulses with high peak pulses are propagated in highly nonlinear fibers.

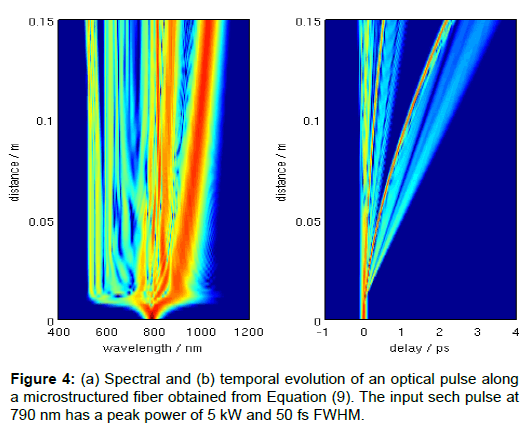
The fission phenomenon can be observed in Figure 4, which shows the temporal and spectral evolution of an optical pulse along a highly nonlinear MOF with hole diameter d=1.4 μm and pitch =1.6 μm. In this case, the dispersion curve has only one zero dispersion wavelength, located at 735 nm. We consider a pump in the anomalous dispersion region at 790 nm, where the nonlinear parameter is λ =117W^-1km^-1. An input pulse is assumed, where P₀=5kW and T₀=28.4fs, which corresponds to an intensity full width at half maximum (FWHM) of 50 fs. For the assumed parameters, we have N=6.02.

A clear signature of soliton fission is the appearance of a new spectral peak in Figure 4a at z = L_fiss. The new spectral peak observed corresponds to the so-called nonsoliton radiation (NSR) [36] or Cherenkov radiation [37] which is emitted by the solitons resulting from the fission process in the presence of higher-order dispersion. When the third-order dispersion coefficient (β₃),the NSR is emitted at wavelengths shorter than that of the soliton, as observed in Figure 4a. Regarding the time domain, Figure 4b shows that a dispersive wave spreads with propagation and lags behind the main soliton.

Another noticeable feature in Figure 4 is the red-shift of the solitons created by the fission process. As a consequence of the SSFS induced by intrapulse Raman scattering, such solitons separate from each other. Since the SSFS is the largest for the shortest soliton, its spectrum shifts the most toward the red side in Figure 4a. The change of the soliton´s frequency determines a reduction in the soliton´s speed because of dispersion. This deceleration appears as a bending of the soliton trajectory in the time domain, as observed in Figure 4b.

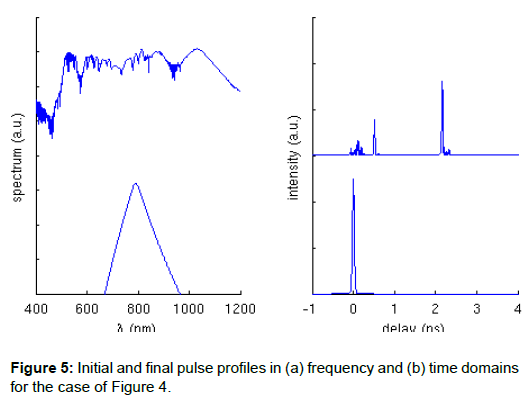
Figure 5 shows the initial and final pulse profiles, both in frequency and time domains. We observe that a nearly uniform supercontinuum is achieved between 500 nm and 1100nm. These features are particularly important for to achieve high performance OCT. In fact, the extreme nonlinear spectral broadening provided by SCG permits a high resolution OCT, while the smooth spectral profile avoids the appearance of side-lobes on the axial point spread function.

Conclusion

The peculiar dispersive characteristics of both tapered and microstrutured fibers make them particularly suitable to generate the supercontinuum using commercially available pump sources around 1060 nm and 800 nm. Pumping with femtosecond pulses in the anomalous dispersion region of the fiber, the soliton fission process gives origin to multiple fundamental solitons of different widths and peak powers. Among the host of soliton related effects, there are two which become then particularly important: the SSFS induced by the Raman scattering and the emission of dispersive radiation. Solitons dominate the long-wavelength edge of the supercontinuum, while the dispersive radiation determines the short wavelength expansion. As a result, a wide and nearly uniform supercontinuum can be achieved. This is important for several applications, namely in the area of optical coherence tomography.

Acknowledgments

The authors acknowledge FCT (Fundação para a Ciência e Tecnologia), FEDER, and the program COMPETE for financial support through project Pest-C/CTM/LA0025/2011.

References

1. Ferreira M (2011) Nonlinear effects in optical fibers. John Wiley & Sons, Hoboken, New Jersey, USA.
2. Broderick NGR, Monroe TM, Bennett PJ, Richardson DJ (1999) Nonlinearity in holey optical fibers: measurement and future opportunities. Opt Lett 24: 1395-1397.
3. Stolen RH, Lin C (1978) Self-phase modulation in silica optical fibers. Rev A 17: 1448-1453.
4. Chraplyvy AR, Stone J (1984) Measurement of crossphase modulation in coherent wavelength-division multiplexing using injection lasers. Electron Electron Lett 20: 996-997.
5. Stolen RH, Bjorkhholm JE, Ashkin A (1974) Measurement of crossphase modulation in coherent wavelength-division multiplexing using injection lasers. Appl Phys Lett 24: 308-310.
6. Dudley JM, Taylor JR (2010) Supercontinuum generation in optical fibers. Cambridge University Press, Cambridge, UK.
7. Humbert G, Wadsworth W, Knight J, Birks T, Russell P, et al. (2006) Supercontinuum generation system for optical coherence tomography based on tapered photonic crystal fibre. Opt Express 14: 1596-1603.
8. Bellini M, Hänsch T (2000) Phase-locked white-light continuum pulses: toward a universal optical frequency-comb synthesizer. Opt Lett 25: 1049-1051.
9. Takara H, Ohara T, Yamamoto T, Masuda H, Abe M (2005) Field demonstration of over 1000-channel DWDM transmission with supercontinuum multi-carrier source. Electron Lett 41: 270-271.
10. Kato T, Suetsugu Y, Takagi M, Sasaoka E, Nishimura M et al. (1995). Measurement of the nonlinear refractive index in optical fiber by the cross-phase modulation method with depolarized pump light. Opt Lett 20: 988-990
11. Knight JC, Birks TA, Russell PSJ, Atkin DM (1996) All-silica single-mode optical fiber with photonic crystal cladding. Opt Lett21: 1547-1549.
12. Russel PSJ (2006) Photonic crystal fibers. J Lightwave Technol 24: 4729-4749.
13. Mogilevtsev D, Birks TA, Russell PSJ (1998) Group-velocity dispersion in photonic crystal fibers. Opt Lett23: 1662-1664.
14. Gander MJ, McBride R, Jones JDC, Mogilevtsev D, Birks TA, et al. (1999) Experimental measurement of group velocity dispersion in photonic crystal fibres. Electron Lett 35: 63-34.
15. Nakajima K, Ohashi M (2002) Dopant dependence of effective nonlinear refractive index in GeO2 and F-doped core single-mode fibers. IEEE Photon Technol Lett 14: 492-494.
16. Cregan RF, Mangan BJ, Knight JC (1999) Single-mode photonic band gap guidance of light in Air. Science 285: 1537-1539.
17. Luan F, Knight J, Russel P, Campbell S, Xiao D, et al. (2004) Femtosecond soliton pulse delivery at 800 nm wavelength in hollow-core photonic bandgap fibers. Opt Express 12: 835-840.
18. Russell P (2003) Photonic crystal fibers. Science 299: 358-362.
19. Broeng J, Mogilevstev D, Barkou S, Bjarklev A (1999) Photonic crystal fibers: a new class of optical waveguides. Opt Fiber Technol 5: 305-330.
20. Eggleton B, Kerbage C, Westbrook P, Windeler R, Hale A et al. (2001) Microstructured optical fiber devices. Opt Express 9: 698-713.
21. Knight JC, Arriaga J, Birks TA, Wadsworth WJ, Russell PSJ (2000) Anomalous dispersion in photonic crystal fiber. IEEE Photon Technol Lett 12: 807-809.
22. Laegsgaard J, Mortenson N, Riishede J, Bjarklev A (2003) Material effects in air-guiding photonic bandgap fibers. J Opt Soc Am B 20: 2046-2051.
23. Saito K, Koshiba M (2005) Numerical modeling of photonic crystal fibers. J Lightwave Technol 23: 3580-3590.
24. Leon-Saval S, Birks T, Wadsworth W, Russel P, Mason M, et al. (2004) Supercontinuum generation in submicron fibre waveguides. Opt Express 12: 2864-2869.
25. Stolen RH, Gordon JP, Tomlinson WJ, Haus HA (1989) Raman response function of silica-core fibers. J Opt Soc Am B 6: 1159-1166.
26. Agrawal GP (2007) Nonlinear fiber optics, Academic Press, Elsevier, San Diego, USA.
27. Blow KJ, Wood D (1989) Theoretical description of transient stimulated Raman scattering in optical fibers. IEEE J Quantum Electron25: 2665-2673.
28. Lin Q, Agrawal GP (2006) Raman response function for silica fibers. Opt Lett 31: 3086-3088.
29. Kodama Y, Hasegawa A (1987) Nonlinear pulse propagation in a monomode dielectric guide. IEEE J Quantum Electron 23: 510-524.
30. Chen CM, Kelley PL (2002) Nonlinear pulse compression in optical fibers: scaling laws and numerical analysis. J Opt Soc Am B19: 1961-1967.
31. Dianov EM, Nikonova ZS, Prokhorov AM, Serkin VN (1986) Optimal compression of multi-soliton pulses in optical fibers. Sov Tech Phys Lett 12: 756-760.
32. Gordon JP (1987) Theory of the soliton self-frequency shift. Opt Lett 11: 659-661.
33. Mitschke F, Mollenauer L (1986) Discovery of the soliton self-frequency shift. Opt Lett 11: 659-661.
34. Husakou A, Herrmann J (2001) Supercontinuum generation of higher-order solitons by fission in photonic crystal fibers. Phys Rev Lett 87: 203901.
35. Akhmediev N., Karlsson M (1995) Cherenkov radiation emitted by solitons in optical fibers. Phys Rev A 51: 2602-2607.