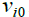Research Article, J Phys Res Appl Vol: 1 Issue: 1
The Effect of Drifting Lighter Ions on Solitary Waves in Heavier, Pair Ion Plasmas with Kappa Described Electrons
Varghese A, Willington NT, Hussein T, Shilpa S and Venugopal C*
School of Pure and Applied Physics, Mahatma Gandhi University, Kottayam, Kerala, India
*Corresponding Author : Chandu Venugopal
School of Pure and Applied Physics, Mahatma Gandhi University, Kottayam, Kerala, India
Tel: (+91) 9446196143
E-mail: cvgmgphys@yahoo.co.in
Received: November 08, 2017 Accepted: December 20, 2017 Published: December 29, 2017
Citation: Varghese A, Willington NT, Hussein T, Shilpa S, Venugopal C (2017) The Effect of Drifting Lighter Ions on Solitary Waves in Heavier, Pair Ion Plasmas with Kappa Described Electrons. J Phys Res Appl 1:1.
Abstract
We investigate the effect of drifting ions on compressive and rarefactive solitary waves in a five component plasma. Heavier pair ions, two components of electrons and drifting lighter ions form the five components. We use the pseudo-potential method to investigate the conditions for the existence of solitary waves. We find that both the Sagdeev potential and amplitudes of solitary waves are dependent on the velocities of the drifting ions: the amplitude of both compressive and rarefactive solitary waves increases with increasing drifting velocities of the lighter ions.
Keywords: Five component plasma; Drifting ions; Rarefactive; Compressive solitary waves
Introduction
A conventional electron-ion plasma supports a wide variety of nonlinear waves. These waves have been thoroughly researched since the path breaking study of Washimi and Taniuti [1], who investigated small amplitude ion acoustic (IA) waves in an unmagnetized plasma consisting of cold ions and hot, isothermal electrons by deriving the well known K-dV equation. At about the same time, Sagdeev [2] used his pseudo-potential approach to study the basic properties of arbitrary amplitude IA solitary waves. This study was quickly extended to plasmas containing two components of electrons with different temperatures [3,4]. More than one component of electrons, gave way to more than one component of ions and Ferrante [5] studied the properties of IA solitons in two and three ion plasmas.
Owing to the ease with which it could be observed, the pioneering studies mentioned above were extended in every possible way. Thus various aspects of IA solitary waves were again explored in two temperature electron plasmas [6-13], multi-ion plasmas [14-21], non- Maxwellian component plasmas [22-32], finite ion temperature plasmas [33,34], pair (electron-positron)-ion plasmas [35,36] and heavier pair ion with another lighter ion component plasmas [37-40]. In addition to the very general plasma compositions and models mentioned above, the effect of streaming plasma components on ion acoustic and dust acoustic solitary waves has also been considered. The effect of streaming ions [41-46], streaming electrons [44,47,48] and even streaming dust [49,50,51] has also been exhaustively investigated.
cometary plasma is a genuine multi-ion plasma. While positively charged oxygen ions were expected to be a component formed by the dissociation of water molecules [52], other positively charged ions such as H2 +, He+, He2 +, C+, OH+, H2O+, H30+, CO+, S+ etc. have also been observed [53,54]. However, it was the unexpected discovery of negative ions, in three broad mass peaks of 7-19, 22-65 and 85-110 amu with energies ranging from .03 to 3.0 keV, that made cometary plasmas genuine multi ion plasmas [55]. And, the unambiguous identification of negatively charged oxygen ions (Oˉ), opened up the exciting prospect of modelling O+ and Oˉ as an ion pair [37,38,40,56].
As regards electrons, observations by the spacecraft ICE at comet Giacobini-Ziner revealed the existence of three components of electrons: a cold, mid, and hot component where the mid component was the photo-electrons generated by the photo-ionization of water molecules [57]. In a related modelling study [58], analysis of gas production rates at comets, noticed a double peak structure of photo-electrons. And in a very recent modelling study, two kappa distributions were fitted to the observations of electrons made at comet 67P/Churyumov-Gerasimenko [59].
Thus our plasma is composed of five components: two components of electrons, both described by kappa distributions, drifting hydrogen ions (to model the solar wind impacting the comet) and positively and negatively charged oxygen ions. Previous studies on the influences of streaming components have been mentioned above.
We find that the plasma supports both rarefactive and compressive solitons [60]. Also the amplitudes of both types of solitons are sensitively dependent on the drift velocity of the lighter ions.
Basic equations
As mentioned above we are interested in studying the effect of streaming ions on IA solitary waves in a five component plasma [61]. The five components are a pair of oppositely charged heavier ions, a streaming lighter ion component and two components of electrons [62] (a hotter solar component denoted by ‘se’ and a colder cometary component of photoelectrons denoted by ‘ce’). The dimensionless distribution of the electron components is given by
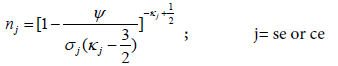 (1)
(1)
In (1) nj is the dimensionless density normalized by its equilibrium value. ѱ is the potential normalized by 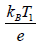 where ‘e’ is the electronic charge and kB is the Boltzmann’s constant. T1 is the temperature of the negatively charged heavier ions.
where ‘e’ is the electronic charge and kB is the Boltzmann’s constant. T1 is the temperature of the negatively charged heavier ions. 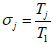 is the dimensionless temperature and κj are the spectral indices [63].
is the dimensionless temperature and κj are the spectral indices [63].
In what follows, ‘i’ denotes streaming ions while the indices 1 and 2 would respectively denote negatively and positively charged heavier ions [64]. Thus the equations of motion for the drifting ions and the heavier ions are given by
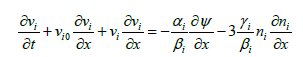 (2)
(2)
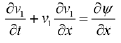 (3)
(3)
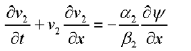 (4)
(4)
In (2) to (4), ‘x’ and ‘t’ have been normalized respectively by 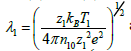 and
and 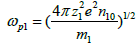 . All velocities are normalized by
. All velocities are normalized by 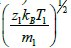 with νi0 now being the normalized drift velocity of drifting ions. Also these adiabatically heated ions obey
with νi0 now being the normalized drift velocity of drifting ions. Also these adiabatically heated ions obey 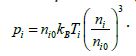
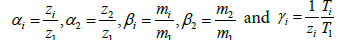 (5)
(5)
In the above, symbols n denote the densities; z, the charge numbers and m, the masses. The normalized equation of continuity for the streaming ion is
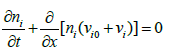 (6)
(6)
While that for the heavier ions is
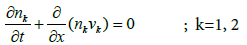 (7)
(7)
Finally, we need the Poisson’s equation, which in its dimensionless form, is given by
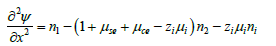
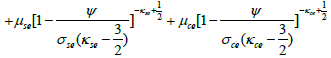 (8)
(8)
In (8)
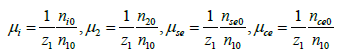 (9)
(9)
where the index ‘0’ indicates equilibrium values of densities.
Nonlinear analysis
We now use equations (2) to (8) for a nonlinear analysis. We therefore define a transformed coordinate ξ = x-Mt where M is the speed of the localized structure moving with the frame [65]. Assuming that all dependent variables are functions of ξ, we can, from (6), obtain the expression for the streaming ion density as
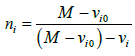 (10)
(10)
Expressions for n1 and n2 can be easily got from (10) by putting νi0 = 0 and replacing νi respectively by ν1 or ν2. Similarly, from (2) we obtain
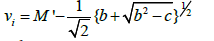 (11)
(11)
Where,
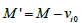
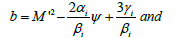 (12)
(12)
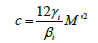
It may be noted at this point that ni reduces to the corresponding expression in Shan and Mushtaq [66] for αi = βi = γi =1. Similar expressions can be obtained for both ν1 and ν2.
Having thus obtained expressions for ni, n1 and n2 and for nse and nce from (1) and substituting into (8) and following standard procedures allows one to write down the energy integral as
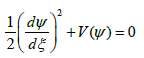 (13)
(13)
Where V(ѱ) is now given by
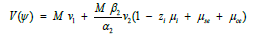
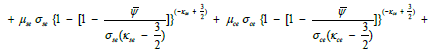 (14)
(14)
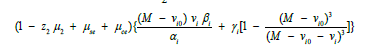
where
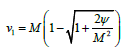 (15)
(15)
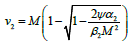 (16)
(16)
As a check on (14) we note that it resembles the expression for the Sagdeev potential in [66] if allowance is made for the extra components in our model. From the condition for the existence of solutions [37,66], we can show that the critical value of M for the existence of the two types of solitons (rarefactive and compressive) is
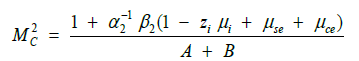 (17)
(17)
where
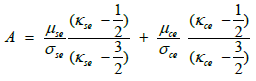
and
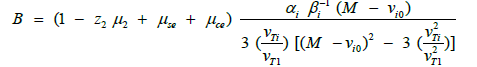
The small amplitude approximation for V(ѱ) is
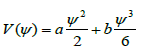 (18)
(18)
where
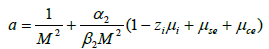
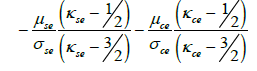
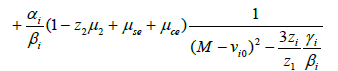 (19)
(19)
and
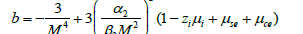
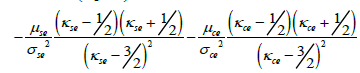 (20)
(20)
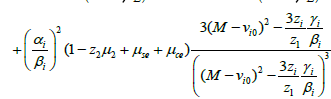
As a check on our results we find that expressions (18) and (19) closely resemble that given in [37] if allowance is made for the fact that we now have drifting ions.
The soliton solutions for potentials of the type (14) is given by [37] as
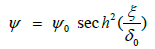
where 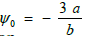 is the amplitude and
is the amplitude and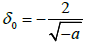 is the width of the soliton.
is the width of the soliton.
Results
Though our relations are applicable to any plasma, we are interested here in parameters relevant to comet Halley. The density of hydrogen ions observed at the comet was ni0 = 4.95 cm-3 with a temperature Ti=8×104 K. The solar electron temperature at the comet was Tse=2×105 K [52]. Hence the temperature of the colder photoelectrons was set at Tce=2×104 K. The Oˉ ions were observed with an energy ~1 eV with densities ≤ 1cm-3 [55]. Thus we keep n10=0.05 cm-3 and n20 = 0.5 cm-3.
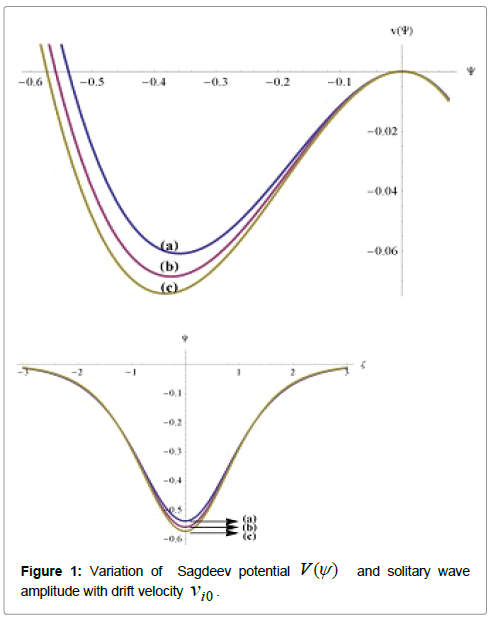
Figure 1 depicts the Sagdeev potential V (ѱ) and soliton structure for the first solution for densities ni0 = 4.95 cm-3, n20 = 0.5 cm-3 and n10 = 0.05 cm-3, temperatures Tse=2×105 K, Tce =1.5×104 K and Ti = 8×104 K, T1=T2=2.8×104 K, charge numbers z1 =5, z2 =3 and zi =1, M = 1.2, spectral indices κse = 3 and κce = 5 as a function of drift velocities νi0 = 0 ( curve (a)), νi0 = 0.4 ( curve (b)) and νi0 = 1.0 ( curve (c)). The figure shows that the depth of the potential V (ѱ) increases with increasing νi0. Also the magnitude of the amplitude of the solitary wave, which is rarefactive in nature, also increases with increasing νi0.
Figure 2 also depicts the Sagdeev potential V(ѱ) and solitary structure for the second solution for densities ni0 = 4.95 cm-3, n20 = 0.5 cm-3 and n10 = 0.05 cm-3, temperatures Tse=2×105 K, Tce =1.5×104 K and Ti = 8×104 K, T1=T2=2.8×104 K, charge numbers z1 =5, z2 =3 and zi =1, M = 1.2, spectral indices κse = 3 and κce = 5 as a function of drift velocities νi0 = 0 ( curve (a)), νi0 = 0.4 ( curve (b)) and νi0 = 1.0 ( curve (c)). The figure shows that the depth of the potential V(ѱ) increases with increasing νi0. Also the magnitude of the amplitude of the solitary wave, which is now compressive in nature, also increases with increasing νi0.
Similar to Figure 1, the amplitude of the rarefactive solitons increases with increasing ni0, Ti and T1 and decreases with increasing κse, z1, z2 and n20. This is true for both νi0 = 1.0 and νi0 ≠ 0 .
And similar to Figure 2, the amplitude of the compressive solitons increases with increasing ni0, Ti and T1 and decreases with increasing κse and n20. This is true for both νi0 = 1.0 and νi0 ≠ 0 .
Also a comparison of Figures 1 and 2 show that the amplitude of rarefactive solitons is of much greater magnitude than the compressive solitons.
Conclusions
We have investigated the effect of drifting lighter ions on rarefactive and compressive solitary waves in a five component cometary plasma. Drifting lighter ions, heavier pair ions and two components of electrons, described by kappa distributions, form the five components. We find that the amplitude of the solitary waves is sensitively dependent on the drift velocities of the lighter ions: the amplitudes increase with increasing drift velocities, increasing lighter ion densities and temperatures of these ions. Thus these solitary waves are most likely to be observed under disturbed solar conditions when these parameters of the solar wind are large. And finally our relations can also be considered as generalizations of earlier studies [37,66].
References
- Washimi H, Taniuti T (1966) Propagation of ion-acoustic solitary waves of small amplitude. Phys Rev Lett 17: 996.
- Sagdeev RZ, Leontovich MA (1966) Cooperative phenomena and shock waves in collisionless plasmas. Rev Plasma Phys 4: 23.
- Jones WD, Lee A, Gleman SM, Doucet HJ (1975) Propagation of ion-acoustic waves in a two-electron-temperature plasma. Phys Rev Lett 35: 1349.
- Goswami BN, Buti B (1976) Ion acoustic solitary waves in a two-electron-temperature plasma. Phys Lett A 57: 149.
- Ferrante G, Nuzzo S, Zarcone M (1979) Ion acoustic solitons in collisionless multi-ion plasmas. Lett Nuovo Cimento 25: 407-416.
- Baboolal S, Bharuthram R, Hellberg MA (1990) Cut-off conditions and existence domains for large-amplitude ion-acoustic solitons and double layers in fluid plasmas. J Plasma Phys 44: 1-23.
- Shahmansouri M, Tribeche M (2014) Propagation properties of ion acoustic waves in a magnetized superthermal bi-ion plasma. Astrophys Sp Sci 350: 623-630.
- Baboolal S, Bharuthram R, Hellberg MA (1989) Arbitrary-amplitude theory of ion-acoustic solitons in warm multi-fluid plasmas. J Plasma Phys 41: 341-353.
- Rice WKM, Hellberg MA, Mace RL, Baboolal S (1993) Finite electron mass effects on ion-acoustic solitons in a two electron temperature plasma. Phys Lett A 174: 416-420.
- Ghosh SS, Ghosh KK, SekarIyengar AN (1996) Large Mach number ion acoustic rarefactive solitary waves for a two electron temperature warm ion plasma. Phys Plasmas 3: 3939.
- Ghosh SS, SekarIyengar AN (1997) Anomalous width variations for ion acoustic rarefactive solitary waves in a warm ion plasma with two electron temperatures. Phys Plasmas 4: 3204.
- Baluku TK, Hellberg MA, Verheest F (2010) New light on ion acoustic solitary waves in a plasma with two-temperature electrons. Europhys Lett 91: 15001.
- Nakamura Y, Sugai H (1996) Experiments on ion-acoustic solitons in a plasma. Chaos Solitons Fractals 7: 1023.
- Bharuthram R., Shukla PK (1992) Large amplitude ion acoustic solitons in a dusty plasma. Planet Space Sci 40: 973.
- McKenzie JF, Verheest F, Doyle TB, Hellberg MA (2004) Compressive and rarefactive ion-acoustic solitons in bi-ion plasmas. Phys Plasmas 11: 1762.
- McKenzie JF, Verheest F, Doyle TB, Hellberg MA (2005) Note on rarefactive and compressive ion-acoustic solitons in a plasma containing two ion species. Phys Plasmas 12: 102305.
- Verheest F, Cattaert T, Hellberg MA (2005) Ion and dust-acoustic solitons in dusty plasmas: Existence conditions for positive and negative potential solutions. Phys Plasmas 12: 082308.
- Yin-Hua C, Wei L, Wen-Hao W (2001) The nonlinear Langmuir waves in a multi-ion-component plasma. Comm Theor Phys 35: 223.
- Yun-Liang W, Zhong-Xiang Z, Yan-Zhen L, Xiao-Dong Ni, Jiang S, et al. (2009) Relativistic magnetosonic solitary wave in magnetized multi-ion plasma. Comm Theor Phys 51: 1121.
- Shahmansouri M, Tribeche M (2014) Ion acoustic solitary waves in bi-ion plasma with superthermal electrons. Astrophys Sp Sci 349: 781.
- Shahmansouri M, Tribeche M (2014) Propagation properties of ion acoustic waves in a magnetized superthermal bi-ion plasma. Astrophys Sp Sci 350: 623.
- Mamun AA (1997) Effects of ion temperature on electrostatic solitary structures in nonthermal plasmas. Phys Rev E 55: 1852.
- Baluku TK, Hellberg MA (2012) Ion acoustic solitons in a plasma with two-temperature kappa-distributed electrons. Phys Plasmas 19: 012106.
- Shahmansouri M (2012) Suprathermality effects on propagation properties of ion acoustic waves. Chin Phys Lett 29: 105201.
- Cairns RA, Mamun AA, Bingham R, Bostrom R, Dendy RO, et al. (1995) Electrostatic solitary structures in non-thermal plasmas. Geophys Res Lett 22: 2709.
- Abassi H, Pajouh HH (2007) Influence of trapped electrons on ion-acoustic solitons in plasmas with superthermal electrons. Phys Plasmas 14: 012307.
- Saini NS, Kourakis I, Hellberg MA (2009) Arbitrary amplitude ion-acoustic solitary excitations in the presence of excess superthermal electrons. Phys Plasmas 16: 062903.
- Dubinova ID, Dubinov AE (2006) The Theory of Ion-Sound Solitons in Plasma with Electrons Featuring the Tsallis Distribution. Tech Phys Lett 32: 575-578.
- Tribeche M, Djebarni L, Amour R (2010) Ion-acoustic solitary waves in a plasma with a q-nonextensive electron velocity Distribution. Phys Plasmas 17: 042114.
- Tribeche M, Amour R, Shukla PK (2012) Ion acoustic solitary waves in a plasma with nonthermal electrons featuring Tsallis distribution. Phys Rev E 85: 037401.
- Shahmansouri M (2013) Influence of suprathermality on the obliquely propagating dust-acoustic solitary waves in a magnetized dusty plasma. Astrophys Sp Sci 344: 153.
- Saini NS, Shalini (2013) Ion acoustic solitons in a nonextensive plasma with multi-temperature electrons. Astrophys Sp Sci 346: 155.
- Tappert F (1972) Improved Korteweg-deVries equation for ion acoustic waves. Phys Fluids 15: 2446.
- Tagare SG (1973) Effect of ion temperature on propagation of ion acoustic solitary waves of small amplitudes in collisionless plasma. Plasma Phys 15: 1247.
- Popel SI, Vladimirov SV, Shukla PK (1995) Ion acoustic solitons in electron–positron–ion plasmas. Phys Plasmas 2: 716.
- Alinejad H, Mamun AA (2011) Oblique propagation of electrostatic waves in a magnetized electron-positron-ion plasma with superthermal electrons. Phys Plasmas 18:112103.
- Sijo S, Sreekala G, Manesh M, Noble PA, Renuka G, et al. (2015) Solitary waves in a plasma with oppositely charged dust (heavier, pair ions) and kappa modeled lighter ions and electrons. Phys Scripta 90: 035601.
- Sijo S, Manesh M, Sreekala G, Neethu TW, Renuka G, et al. (2015) Oblique solitary waves in a five component plasma. Phys Plasmas 22: 123704.
- Sijo S, Manesh M, Sreekala G, Anu V, Venugopal C (2017) Fast and slow mode solitary waves in a five-component plasma. Braz J Phys 47: 46-54.
- Manesh M., Sijo S, Anu V, Sreekala G, Neethu TW, et al. (2017) Effect of anisotropy of lighter and heavier ions on solitary waves in a multi-ion plasma. Phys Plasmas 24: 062905
- Jin-Yuan L, Jin-Xiu MA (1997) Dust-acoustic soliton in a streaming plasma. Chinese Phys Lett 14: 432
- Zheng-Xiong W, Wang X, Li-Wen-Ren, Jin-Yuan Liu, Yue Liu (2005) Dust-acoustic soliton in electronegative complex plasmas with streaming positive ions. Phys Plasmas 12: 082104.
- Yunliang W, Zhongxiang Z, Xiangqian J, Ni X, Yu Z, et al. (2009) Dust acoustic wave in a dusty plasmas with streaming ions and non-adiabatic dust charge variation. Phys Lett A 373: 2944.
- Barmen SN, Talukdan A (2011) Effect of ion and electron streaming on the formation of ion-acoustic solitons in weakly relativistic magnetized ion-beam plasmas. Int J Appl Math Computation 3: 283.
- Paul I, Pakira G, Chattopadhyay SK, Paul SN, Ghosh, B (2012) Analytical study on the existence of ion-acoustic solitary waves in a plasma consisting of warm streaming ions and nonthermal electrons. Ind J Phys 86: 395-400.
- Prathana B, Saurav B, Nilakshi D (2016) Dust ion acoustic solitary and shock waves in strongly coupled dusty plasma in presence of attractive interparticle interaction potential. Phys Plasmas 23: 103706.
- Das R., Kumar R (2012) Drifting effect of electrons on dust ion acoustic solitary waves in unmagnetized plasma. Int J Recent Res Appl Stud 10: 280.
- Mondal KK, Roy CA, Paul SN (1998) Effect of Boundary, Electron Inertia and Streaming on Large Amplitude Waves in a Relativistic Plasma. Phys Scr 57: 652.
- Mahmood S, Mushtag A (2002) Dust streaming effect on dust acoustic solitary wave in magnetized dust-ion plasmas. J Fus Energy 21: 199.
- Chatterjee P, Jana RK (2005) Speed and shape of dust acoustic solitary waves in the presence of dust streaming. Z Naturforsch 60: 275.
- Sahoo H, Mondel KK, Ghosh B (2016) Effect of dust streaming on linear and nonlinear electrostatic waves in magnetized plasma. J Phys Chem Sci 4:1.
- Brinca AL, Tsurutani BT (1987) Unusual characteristics of electromagnetic waves excited by cometary newborn ions with large perpendicular energies. Astro Astrophys 187: 311-319.
- Balsiger H, Altwegg K, Bühler F, Geiss J, Ghielmetti AG, et al. (1986) Ion composition and dynamics at comet Halley. Nature 321: 330-334.
- Rubin M., Kenneth CH, Tamas IG, Michael RC, Kathrin A, et al. (2009) Ioncomposition and chemistry in the coma of comet 1P/Halley-A comparison between Giotto's ion mass spectrometer and our ion-chemical network. Icarus 199: 505.
- Chaizy P, Reme H, Sauvaud JA, D'Uston C, Lin RP, et al. (1991) Negative ions in the coma of comet Halley. Nature 349: 393-396.
- Manesh M., Neethu TW, Neethu J, Sijo S, Sreekala G (2016) Korteweg–deVries–Burgers (KdVB) equation in a five component cometary plasma with kappa described electrons and ions. J Theor Appl Phys 10: 289-296.
- Zwickl RD, Baker DN, Bame SJ, Feldman WC, Fuselier SA, et. al (1986) Three component plasma electron distribution in the intermediate ionized coma of comet Giacobini-Zinner. Geophys Res Lett 13: 401.
- Bharadwaj A (2003) On the solar EUV deposition in the inner comae of comets with large gas production rates. Geophys Res Lett 30: 24.
- Broiles TW, Livadiotis G, Burch JL, Chae K, Clark G, et al. (2016) Characterizing cometary electrons with kappa distributions. J Geophys Res 121: 7407.
- Paul SN, Mondal KK, Roychowdary A (1999) Effects of streaming and attachment coefficients of ions and electrons on the formation of soliton in a dusty plasma. Phys Lett A 257: 165.
- Paul SN, Chattopadhyay S, Bhattacharya SK, Bera B (2003) On the study of ion-acoustic solitary waves and double-layers in a drift multicomponent plasma with electron-inertia. Pramana 60: 1217-1233.
- Misra AP, Adhikary NC (2011) Large amplitude solitary waves in ion-beam plasmas with charged dust impurities. Phys Plasmas 18: 122112.
- Shahmansouri M, Tribeeha M (2014) Large amplitude dust ion acoustic solitons and double layers in dusty plasmas with ion streaming and high-energy tail electron distribution. Comm. Theor Phys 61: 377.
- Lakhina GS, Singh SV, Kakad AP (2011) Ion and electron-acoustic solitons and double layers in multi-component space plasmas. Adv Sp Res 47: 1558.
- Saberian E, Esfandyari-Kalejahi A, Rastkar-Ebrahimzadeh A, Afsari-Ghazi M (2013) Propagation of ion-acoustic solitons in an electron beam-superthermal plasma system with finite ion-temperature: Linear and fully nonlinear investigation. Phys Plasmas 20: 032307.
- Shan SA, Mushtaq A (2012) Arbitrary dust ion acoustic soliton with streaming ions and superthermal electrons. Phys Scr 86: 035503.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi