Review Article, J Electr Eng Electron Technol Vol: 11 Issue: 8
A Comparative Study between Genetic Algorithms and Particle Swarm Optimization Applied to Power System Using Multi Objective Function
Ghouraf Djamel Eddine1*, Naceri Abdellatif2 and Sayeh Abdelkader1
1Department of Electrical Engineering, University of Oran, National Polytechnic School, SCAMRE Laboratory , BP1523 EL M’naour, Oran 31000, Algeria
2Department of Electrical Engineering, DL University of SBA, IRECOM Laboratory, BP 98 22000, Algeria
*Corresponding Author: Ghouraf Djamel Eddine
Department of Electrical Engineering,
University of Oran,
National Polytechnic School,
SCAMRE Laboratory ,
BP1523 EL M’naour,
Oran 31000,
Algeria,
Tel: + 555563532;
E-mail: djamel-eddine.ghouraf@enp-oran.dz
Received date: 30 December, 2022, Manuscript No. JEEET-22-62041;
Editor assigned date: 02 January, 2023, PreQC No. JEEET-22-62041 (PQ);
Reviewed date: 17 January, 2023, QC No. JEEET-22-62041;
Revised date: 25 January, 2023, Manuscript No. JEEET-22-62041 (R);
Published date: 02 February, 2023, DOI: 10.4172/2325-9833.1000921
Citation: Eddine GD, Abdellatif N, Abdelkader S (2023) A Comparative Study between Genetic Algorithms and Particle Swarm Optimization Applied to Power System Using Multi Objective Function. J Electr Eng Electron Technol 12:1.
Abstract
In this paper, meta-heuristic techniques using genetic algorithms GA and particle swarm optimization PSO to tuning optimal design of power system stabilizer PSS proposed. This latter have been used for many years to add damping to electromechanical oscillations of power system, Based on this idea we have proposed multiobjective function composed with tow function, first maximize stability margin by increasing the damping factors while minimizing the real parts of the eigenvalues. Simulation results to comparative study between genetic algorithms and particle swarm optimization obtained by our realized Graphical User Interface (GUI) proved the efficiency of PSS optimized by genetic algorithms in comparison with particle swarm optimization, showing stable system responses almost insensitive to large parameter variations and under different operating regime (under-excited, nominal and over excited regime).
Keywords: Power System Stabilizer (PSS); Genetic
Algorithms (GA); Particle Swarm Optimization (PSO);
Multiobjective function; Graphical Interface (GUI)
Introduction
The electrical energy has become the major form of energy for end use consumption in today’s world. There is always a need of making electric energy generation and transmission, both more economic and reliable. The voltages throughout the system are also controlled to be within ± 5% of their rated values by automatic voltage regulators acting on the generator field exciters, and by the sources of reactive power in the network [1].
Stability and robustness are considered essential requirements for friability and continuity of electrical energy production this latter produced by a series of systems with very complex mathematical models called power system. Since these systems installed in complex environmental conditions they are exposed to a variation uncertainty which affected directly in the operation of these systems and therefore the stability of the energy production power system stabilizer PSS plays an important role in improving the stability of power systems [2].
The parameters of CPSS are determined based on the linearized model of the power system. Providing good damping over a wide operating range, the CPSS parameters should be fine tuned in response to both types of oscillations. Since power systems are highly nonlinear systems, with configurations and parameters which alter through time, the CPSS design based on the linearized model of the power system cannot guarantee its performance in a practical operating environment. Therefore, an adaptive PSS which considers the nonlinear nature of the plant and adapts to the changes in the environment is required for the power system [3]. In order to improve the performance of CPSSs, numerous techniques have been proposed for designing them, such as intelligent optimization methods [4-6] and fuzzy logic method [7,8].
Meta-heuristic techniques are a new family of stochastic algorithms which aim to solve difficult optimization problems. Used to solve various applicative problems, these methods have the advantage to be generally efficient on a large amount of problems.GA and PSO belonged to population approaches. Meta heuristics are generally used to solve a simplified Optimal Power Flow (OPF) problem such as the classic economic dispatch, security constrained economic power dispatch, and reactive optimization problem, as well as optimal reconfiguration of an electric distribution network [9].
Genetic Algorithms (GAs) were invented by John Holland in the 1960s and were developed by Holland and his students and colleagues at the University of Michigan in the 1960's and the 1970's. In contrast with evolution strategies and evolutionary programming, Holland's original goal was not to design algorithms to solve specific problems, but rather to formally study the phenomenon of adaptation as it occurs in nature and to develop ways in which the mechanisms of natural adaptation might be imported into computer systems [10,11].
The Particle Swarm Optimization (PSO) strategy is a new class of algorithms proposed to solve continuous optimization problems [12-14]. The Particle Swarm Optimizer was introduced by James Kennedy and Russell Eberhart in 1995. Inspired by social behavior and movement dynamics of insects, birds and fish, it is also related, however, to evolutionary computation, and has links to both genetic algorithms and evolution strategies.
In this paper, the problem of robust PSS design is formulated as a multi objective optimization problem by GA and PSO are used to solve this problem applied in the automatic excitation regulator of powerful synchronous generators to improve power system stability.
Power system model
The dynamic performance study and stability analysis of power system requires faithful mathematical models capable to contain all the system studied comportment for it we used in this work on permeances networks modeling based on PARK-GARIVE model of powerful synchronous generators for eliminating simplifying hypotheses and testing the control algorithm. The PSG model is defined by equations 1 to 4 (Figure 1) [15].
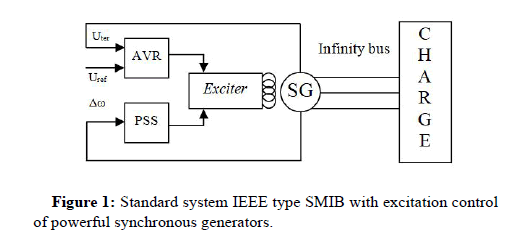
Figure 1: Standard system IEEE type SMIB with excitation control of powerful synchronous generators.
• Currants equations
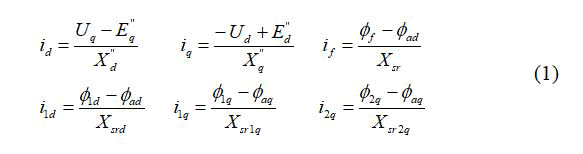
• Voltage equations
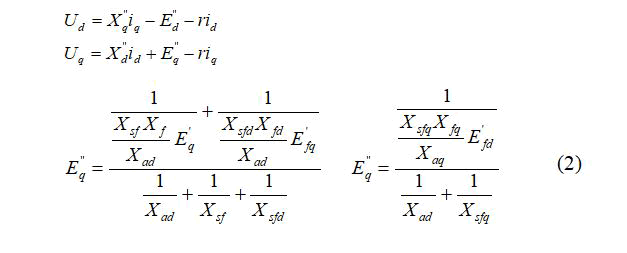
• Flow equations
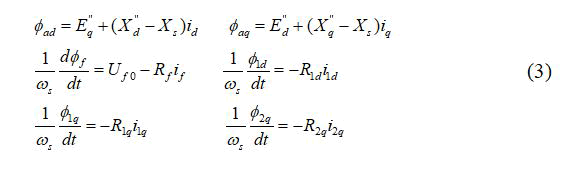
• Mechanical equations
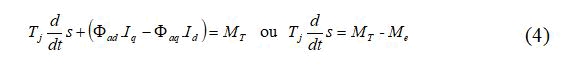
Meta-heuristics
The new paradigms were called meta-heuristics and were first introduced at mid-80's as a family of searching algorithms able to approach and solve complex optimization problems, using a set of several general heuristics. The term meta-heuristic was proposed in to define a high level heuristic used to guide other heuristics for a better evolution in the search space [16]. Although traditional stochastic search methods are mainly guided by chance (solutions change randomly from one step to another), they can be used in combination with meta-heuristic algorithms to guide the search process and to accelerate the convergence.
Most meta-heuristics algorithms are only approximation algorithms, because they cannot always find the global optimal solution. But the most attractive feature of a meta-heuristic is that its application requires no special knowledge on the optimization problem to be solved, hence it can be used to define the concept of general problem solving model for optimization problems or other related problems [17,18]. Since their introduction in the mid-80s till now, meta-heuristic methods for solving optimization problems have been continuously developed, allowing addressing and solving a growing number of such problems, previously considered difficult or even impossible to solve. These methods include simulated annealing, tabu search, evolutionary computation techniques, artificial immune systems, genetic algorithms, particle swarm optimization, ant colony algorithm, differential evolution, harmony search, honey-bee colony optimization etc. The next section presents a brief review of basic issues for the most commonly used met-aheuristics cited above. Several applications of these methods in the field of power systems.
In this work we based on genetic algorithms, particle swarm optimization techniques.
Genetic algorithms
Genetic Algorithm (GA) is a search technique that mimics the mechanisms of natural selection, discovered by John Holland in 1970 [19]. Cell is the building unit of all living organisms. In each cell there is a set of chromosomes which are strings of DNA. Every chromosome consists of genes which encode a particular protein. During reproduction, first occurs crossover. Genes from parents form in some way the whole new chromosome. However, the new created offspring can be mutated. Mutation occurs when the elements of DNA are a bit changed.
These changes are mainly caused by errors in copying genes from parents. The fitness of an organism is measured by success of the organism in its life. With generations, the good characteristics remain and the bad ones died which represents “the survival of the fittest”.
Many work realized on optimization by genetic algorithms to tuning power system stabilizer parameters for adaptation and reliability of this techniques to power system.
Particle swarm optimization
Particle swarm optimization is a population based stochastic optimization method [20]. Explores for the optimal solution from a population swarm of moving particle vectors, based on a fitness function. Each ith particle vector represents a potential answer and has a position (Xik) and a velocity (Vik) at the kth iteration in the problem space. Each ith vector keeps a record of its individual best position (Pik), which is associated with its own best fitness it has achieved so far, at any kth step in the iteration process. This value is known as pbesti. Moreover, the optimum position among all the particles obtained so far in the swarm is stored as the global best position (Pgk). This location is called gbest. The new velocity of particle will be updated according to the following equation:
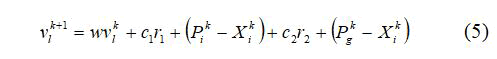
where w is an inertia weight in the first part that represents the memory of a particle during a search, c1 and c2 are positive numbers illustrating the weights of the acceleration terms that guide each particle toward the individual best and the swarm best positions respectively, r1 and r2 are uniformly distributed random numbers in (0,1), and N is the number of particles in the swarm. The second and the third parts of (6) represent cognitive part and social part respectively. The inertia weighting function in (5) is usually calculated using the following equation:
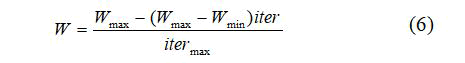
Where wmax and wmin are the maximum and minimum values of w respectively, itermax is the maximum number of iterations and iter is the current iteration number. The first term in (5) enables each particle to perform a global search by exploring a new search space. The last two terms in (5) enable each particle to perform a local search around its individual best position and the swarm best position. Each particle changes its position based on the updated velocity according to the following equation:
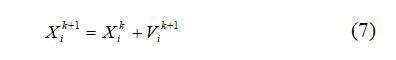
The difference between GA and PSO
The PSO algorithm share many common points with the genetic algorithm (GA). Both algorithms start with a population of individuals randomly generated; all both have objective function values for evaluating the population. Both algorithms days start with the population and seek optimum random technical. The two systems do not guarantee success. They also have the memory, which is important for the algorithm. Such as genetic algorithms, PSO is based on populations that slowly converge to one or more solutions. However, with PSO, the particles are preserved throughout the entire process; they do not die. Contrary to the genetic algorithm, this is based on competition for the best chance of survival and reproduction. PSO uses a type of cooperation between the molecules; this is realized by exchanging the coordinates of the best solutions which have been produced up to this point. PSO traditionally has no crossover between individuals, and has no mutation and the particles are never replaced by other individuals during execution. Instead of that PSO refines its research by attracting the particles. Table 1 it gives us the difference between GA and PSO.
Table 1: A comparative between GA and PSO.
Tuning power system stabilizer parameters based GA and PSO multi objective function
Objectives functions
The choice of objectives functions generally based on the needs of our controlled system. The purpose of the PSS use is to ensure satisfactory oscillations damping, and ensure the overall system stability to different operation points [21]. To meet this goal, we using a function composed of two multiobjective functions based enslavement theory:
• To ensure satisfactory oscillations damping we must increase damping coefficient ζ, this latter defined for system stable.
• To improve system stability we must minimizing the real parts σ of the eigenvalues of the system.

Representation of these parameters defined by Figure 2.
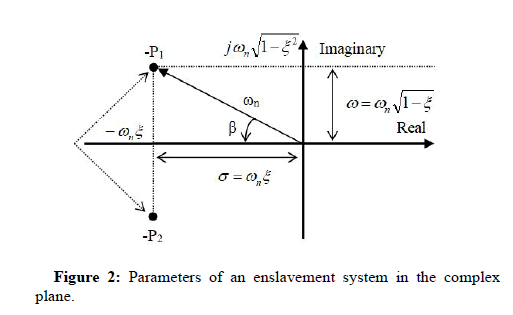
Figure 2: Parameters of an enslavement system in the complex plane.
A base on tow enslavement notion we proposed the flowing multi objective function.
max(ζ)-min(σ) (9)
Fobj=max (max(ζ)-min(σ)) (10)
Optimization results
To optimize and study power system we created graphical user interface GUI (Figure 3) under MATLAB this latter allows to:
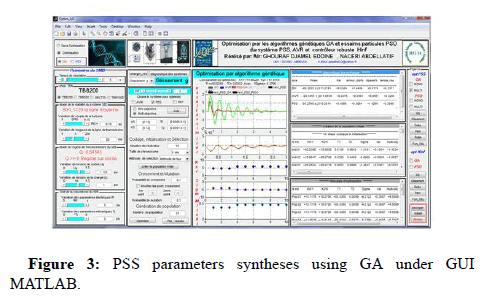
Figure 3: PSS parameters syntheses using GA under GUI MATLAB.
• To optimized controller parameters by genetic algorithms and particle swarm optimization.
• View system regulation results and simulation.
• Calculate system dynamic parameters.
• Test system stability and robustness.
For SMIB system stability study we have performed perturbations by abrupt variations of turbine torque ΔTm of 15% at t=1 second.
We simulated SMIB system under
• Different operations regime: under-excited, the rated and the overexcited.
• Different transition line: long, court and average
• Different synchronies generators: TBB 200, 500, 1000 and BBC720.
We optimized controller parameters by GA and PSO under different condition cited above.
GA optimization method
To run GUI for optimization by genetic algorithms we use optimization/GA/PSS/multi objective.
Optimization example using GA technique with Number of individuals=10 , Number of population=10 (Table 2).
Table 2: Optimization process by using GA technique.
The optimized parameters: K1=+11.9529 K2=+11.8118 T1= +00.0216 T2=0.0232 Sigma= -5.2799 Ksi=+0.4568, multiobj=5.7367
PSO optimization method
To run GUI for optimization by particle swarm we use optimization/PSO/PSS/multiobjective (Figure 4).
Figure 4: PSS parameters syntheses using PSO under GUI MATLAB.
Optimization example using PSO technique with Number of individuals=10, Number of population=10 (Table 3).
Table 3: Optimization process by PSO initialization and algorithm. Optimization is completed.
The optimized parameters
K1=+10.2320 K2=+10.3196 T1=+00.0606 T2=0.0195 Sigma=-2.0428 ksi=+0.1517 multi-obj=+5.0645
The optimization results obtained examples and Figure 5 show that: GA and PSO optimizations techniques well adapted to multiobjective function:
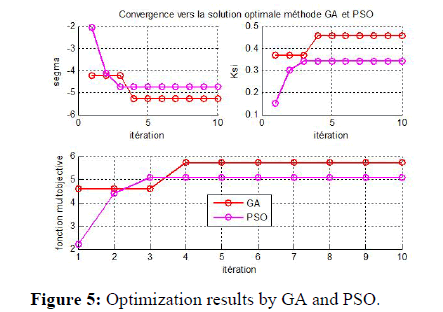
Figure 5: Optimization results by GA and PSO.
• Increase damping coefficient ζ (b).
• Decrease real part of pole σ (a).
• Increase multiobjective function (c).
GA (GA_Multi=+5.7367) more reliable than PSO (PSO_Multi= +5.0645).
Table 4 present analyze static and dynamic performances of power system calculated under GUI realized with long transmission line and different values of reactive power (under excited, nominal, and over excited) for TBB 200. PSS parameters optimized using GA and PSO.
Table 4: PSS parameters optimized using multi objective GA and PS.
With:
• ε %: the static error.
• t: the settling time for 5%.
• d%: the maximum overshoot.
• Poles.
The following results were obtained by studying the SMIB in the following cases: opened Loop and Closed Loop System with PSS, PSS-GA and PSS-PSO.
Simulation results
From table results, it can be observed that the use of PSS-GA and PSS-PSO improves considerably the dynamic performances by damping coefficient ζ and improves stability by decrease real part of pole σ under different operating regime. However optimization by the genetic algorithm in the majority of results obtained very effective compared the use of particle swarms optimization.
Figures 6,7 and 8 show simulation results of power system studied under different regime with: a:'s' variable speed, b:'delta' the internal angle.
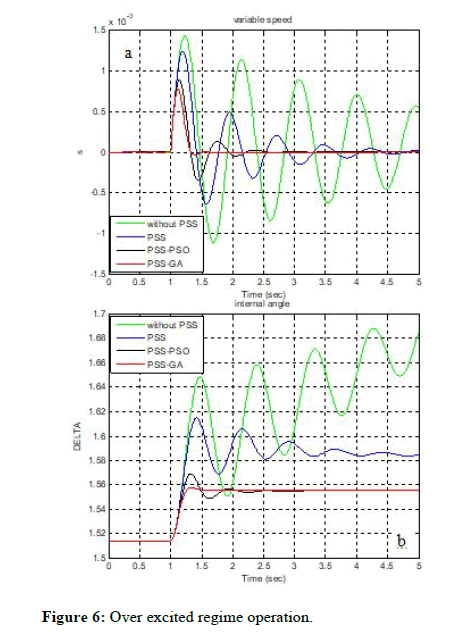
Figure 6: Over excited regime operation.
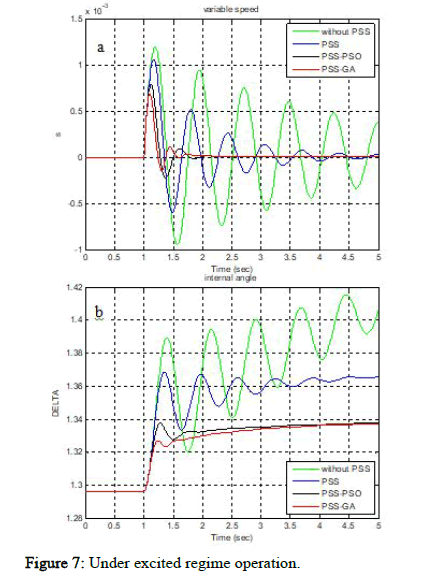
Figure 7: Under excited regime operation.
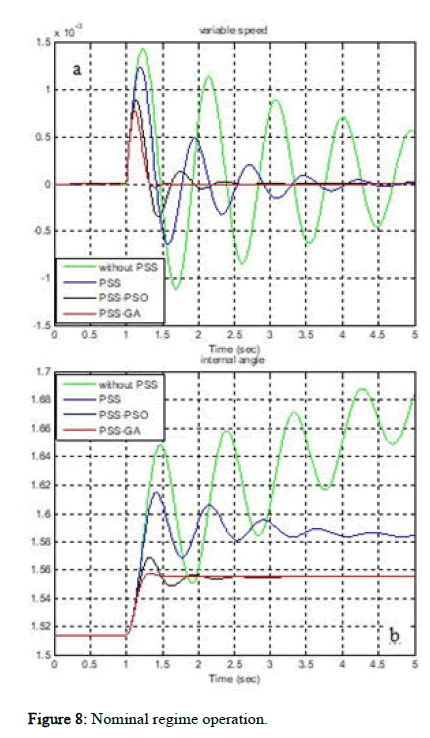
Figure 8: Nominal regime operation.
The simulation results shown in Figures 7 and 8 show the effectiveness of the use of GA and PSO optimization techniques in comparison with conventional PSS and open loop, it can be observed static errors negligible so better precision, and very short setting time so very fast system, and we found that after few oscillations, the system returns to its equilibrium state even in different regime operation.
The optimization and simulation results satisfy to show the reliability of the proposed optimization technique (GA).
Conclusion
In this article, we have optimized the PSS parameters by Genetic Algorithm and Particle Swarm Optimization for comparative study; these optimized PSS are used for powerful synchronous generators exciter voltage control in order to improve static and dynamic performances of power system.
Genetic algorithm technique optimization allows us to obtain a considerable improvement in dynamic performances and robustness stability of the SMIB studied. The optimization and simulation results show that the optimization by the genetic algorithm very effective in comparison with the particle swarms optimization. All results are obtained by using our created GUI/MATLAB
References
- Das TK, Venayagamoorthy GK (2006) Optimal design of power system stabilizers using a small population based PSO. In2006 IEEE Power Engineering Society General Meeting, June 18-22, Montreal, QC, Canada, 7.
- Ghouraf de (2010) Study and Application of the advanced frequency control techniques in the voltage automatic regulator of Synchronous machines. Magister Thesis, UDL-SBA, French.
- Boroujeni SMS, Hemmati R, Delafkar H, Boroujeni AS (2011) Optimal PID power system stabilizer tuning based on particle swarm optimization. Indian J Sci Technol 4:378-383.
- Sumathi N, Selvan MP, Kumaresan N (2007) A hybrid genetic algorithm based power system stabilizer. International Conference on Intelligent and Advanced Systems. November 25-28, Kuala Lumpur, Malaysia, 876-881.
- Jiang P, Yan W, Gu W (2008) PSS parameter optimization with genetic algorithm. In 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, April 06-09, Nanjing, China, 900-903.
- Yassami H, Darabi A, Rafiei SMR (2010) Power system stabilizer design using strength pareto multiobjective optimization approach. Electr Power Syst Res 80:838–846.
- Dubey M (2007) Design of genetic algorithm based fuzzy logic power system stabilizers in multi machine power system. International Conference on soft computing and intelligent systems, Stevens Point, Wisconsin, USA, 214-219.
- Hwanga GH, Kimb DW, Leec JH, Joo Y (2008) Design of fuzzy power system stabilizer using adaptive evolutionary algorithm. Eng Appl Artif Intell 21:86–96.
- Jizhong Z (2009) Optimization of power system operation. IEEE Press Editorial Board WILEY, Canada, 664.
- Dhubkarya DC, Nagariya D, Kumar J (2010) Function Optimization Using Genetic Algorithm by VHDL. Glob J Comput Sci Tech 10:73-77.
- Mitchell M (1999) An Introduction to Genetic Algorithms. A Bradford Book, The MIT Press, Cambridge, Massachusetts, London, England, 1-158.
- Carlisle A, Dozler G (2002) Tracking changing extrema with adaptive particle swarm optimizer. In Proceedings of the 5th biannual world automation congress, June 09-13 Orlando, FL, USA, 265-270.
- Schutte F (2005) The Particl Swarm Optimization Algorithm. Structural Optimization. 2005. EGM 6365.
- Mekhanet M, Mokrani L, Lahdeb M (2012) Comparison between Three Metaheuristics Applied to Robust Power System Stabilizer Design. Acta Electr Tehnic 53:41-49.
- Smolovik SV (1988) Mathematical modeling method of transient processes synchronous generators most usual and non-traditional in the electro-energy systems. "PhD Thesis State, Leningrad Polytechnic Institute, Russia.
- Glover F (1986) Future Paths for Integer Programming and Links to Artificial Intelligence. Comput Oper Res 13:533–549.
- Lee KY, El-Sharkawi (2008) Modern Heuristic Optimization Techniques with Applications to Power Systems. IEEE Press Series on Power Engineering, John Wiley and Sons, Wasington.
- Gavrilas M (2010) Heuristic and metaheuristic optimization techniques with application to power systems. In Proceedings of the 12th WSEAS international conference on Mathematical methods and computational techniques in electrical engineering (MMACTEE'10). World Scientific and Engineering Academy and Society (WSEAS), Stevens Point, Wisconsin, USA, 95–103.
- Holland JH (1975) Adaptation in natural and artificial systems: An introductory analysis with applications to biology, control, and artificial intelligence. U Michigan Press merican Psychological Association, 750 First Street NE, Washington.
- Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings of the IEEE international conference of neural network (ICNN’95), 27 November-01 December, Perth, WA, Australia. 1942–1948.
- Eddine GD (2016) Power System Stabilizer Design Based a PSO Multiobjective Function Implemented Under Graphical Interface. Commun Inf Technol J 10:27-33.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi