Research Article, Res Rep Metals Vol: 1 Issue: 2
Atomistic Monte Carlo Simulations on the Melting Transition of Iron at Ambient Pressure
Khanna R1*, Sahajwalla V1 and Seetharaman S2
1Centre for Sustainable Materials Research and Technology, School of Materials Science and Engineering, The University of New South Wales, NSW 2052, Sydney, Australia
2Department of Materials Science and Engineering, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
*Corresponding author: Rita Khanna
Associate Professor, Centre for Sustainable Materials Research and Technology, School of Materials Science and Engineering, The University of New South Wales, NSW 2052, Sydney, Australia
Tel: 61-2-9385 5589
Fax: 61-2-9385 4292
E-mail: ritakhanna@unsw.edu.au
Received: March 27, 2017 Accepted: April 27, 2017 Published: May 01, 2017
Citation: Khanna R, Sahajwalla V, Seetharaman S (2017) Atomistic Monte Carlo Imulations on the Melting Transition of Iron at Ambient Pressure. Res Rep Metals 1:2.
Abstract
Atomistic computer simulations are playing an increasingly important role in high temperature processes, bridging the gap between theory and experiment, and taking cutting edge research into unchartered territories. A fundamental understanding of the melting behaviour of BCC iron is of great significance in steelmaking operations. We report Monte Carlo simulations on the melting transition of iron using three well known interaction potentials, namely the Rosato potential, the Mendelev potential and the Sutton-Chen potential. Depending on the potential used, the interactions between iron atoms varied from 1/r2, as well as 1/r8.14 at short distances, and the range of applicability was found to vary from 3.5 Å to 9.5 Å. These atomic level computer simulations were carried out using a range of simulation variables such as the size of the simulation cell, step size, boundary conditions and statistical ensemble. The melting transition was identified clearly in all cases through discontinuities in energy and increases in local disorder. The simulation data however showed a significant scatter. Interaction potentials of iron based on system characteristics at 0 K were found somewhat limited for quantitative high temperature simulations (~1800K). Iron potentials developed for earth science applications were not found to be suitable for these investigations. These computer simulations therefore point towards a significant gap in the knowledge base in the atomistic modelling of molten iron, especially for steelmaking applications.
Keywords: Interatomic; Potentials; Iron; Monte Carlo Simulations; Phase transformation; Melting; Disorder
Introduction
Atomistic computer simulation is an important technique for developing a fundamental understanding of materials and processes; these can act as a bridge between models and theoretical predictions on one hand, and experimental observations on the other. A number of researchers have carried out computer simulations on the melting point of iron using a variety of interaction potentials [1-4]. There was a significant variation in simulation results and the melting transition of iron was found to occur at temperatures ranging from 1800K to 2400K (experimental M.P of iron: 1812K). A small change in temperature can significantly affect the kinetics of steelmaking reactions such as various reduction reactions, carburization and decarburization of molten steel, the role played by surface active elements, etc. [5,6]. A direct correlation needs to be established between the simulation and experimental temperatures so that simulation results and associated implications could be used for predicting and understanding experimental behaviour and phenomena. Using a lattice gas model, our group was successful in developing such a correlation for the saturation solubility of carbon in molten iron in the temperature range 1750-1850 K [7,8].
However, when significant discrepancies are observed between results from computer simulations and experiments, it is important to understand the underlying reasons, test the validity of assumptions used and limitations, if any, of the simulation approach. In this article, we report detailed computer simulations on the melting transition in BCC iron. Our aim is to develop a fundamental understanding of factors influencing the onset of local disorder and the melting transition during atomistic simulations. Three key factors, namely the choice of interaction potential, the nature of the statistical ensemble (NVT: fixed number of particles, volume and temperature; or NPT: fixed number of particles, pressure and temperature) used, and the amplitude of the step size during a simulation move, were investigated. These atomistic computations were carried out using standard Monte Carlo simulation methods and algorithms [9]. The simulation of dynamic processes using the conventional density functional theory (DFT) however requires time and length scales many orders of magnitude higher than currently feasible [10]. A few hybrid techniques have been developed that utilize DFT methods for the computation of configuration free energies at zero Kelvin, followed by Monte Carlo or molecular dynamics simulations at high temperatures [11].
Iron and its alloys have been investigated extensively because of their importance in key scientific and technical areas of magnetism, steelmaking, and for processes taking place in earth’s outer core. A large number of interaction potentials have been reported in the literature for both solid and liquid iron [12-25]. Most of these interatomic potentials were developed semi-empirically by fitting data for perfect crystals at zero Kelvin. The fitting of various potential parameters was carried out using standard properties of iron such as lattice constant, cohesive energy, vacancy formation energy, elastic constants etc. [12-20]. Computer simulations based on such potentials are usually carried out in the constant volume NVT ensemble. On the other hand, iron potentials developed for earth sciences applications are used to investigate the properties of molten iron at extremely high temperatures (up to 6000K) and pressures (up to 300 GPa) [22-25]. These simulations are generally carried under the constant pressure NPT ensemble. However, the operating conditions for the steelmaking process (P= 0.1 MPa (1 bar) & T=1700-1900 K) are in the middle of the two extreme scenarios detailed above. The extrapolation of a potential’s range of validity up from 0 K to 1800K, or down from 300 GPa pressure to atmospheric pressure (0.1 MPa) & from 6000 K to 1800K is a nontrivial exercise. Although a few potentials have been reported for Fe-C alloys in the solid state [26], to the best of our knowledge, interaction potentials have not been developed specifically for steelmaking conditions.
Multi-body Finnis-Sinclair potentials [16-19] and embedded atom potentials represent state of the art for cohesion studies in metallic iron [18]. It has been recognised that pair-potentials are not able to properly reproduce metallic cohesion; it is customary to add a volume dependent term in the total energy by analogy with perturbation theory. Based on second moment approximation in the tight-binding theory, multi-body interactions contribute as embedding energy to the system potential. This potential term represents the background contributions from all neighbours to the force exerted by one atom on another. Finnis and Sinclair [16] used a square root functional form to represent this term; Mendelev et al. have used an additional a square functional form in their embedding energy term [18]. Based on experimental data and first principle calculations, a number of angle-dependent bond-order potentials have also been reported for BCC/FCC iron [20,21]. In this article, we have carried out atomistic simulations on BCC iron using three well-known potentials: Rosato potential (Finnis-Sinclair approach, [17]), Mendelev et al. potential (EAM approach, [19]) and Sutton-Chen potential (a long range potential for earth sciences applications, [22]).
This article is organised as follows. Details of various iron potentials used are presented in Section 2; a critical analysis and comparison was also carried out on their ranges of applicability, specific features and limitations if any. Algorithms used for Monte Carlo simulations in both NVT and NPT ensembles are presented in Section 3 along with the simulation criteria used for determining the onset of melting transition. Simulation results for various interaction potentials using two statistical ensembles and simulation variables are presented in Section 4. These are followed by a critical analysis, discussion and conclusions that could provide guidelines for making an appropriate choice of interaction potentials and simulation conditions for atomistic investigations on molten iron at steelmaking temperatures.
Interaction Potentials for Iron
Three well-known interaction potentials for iron were investigated in these simulations. The specific features of these potentials are detailed below:
Rosato potential
Based on many-body Finnis-Sinclair (FS) approach, the total energy of an assembly of atoms at positions Ri is written as
Utot = Un + Up (1)
Un represents the cohesive band energy and Up is the repulsive core-core interaction. Using a pair-wise potential V, Up can be written as
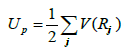 (2)
(2)
A quadratic polynomial was used to represent the pair potential V(r)
V(r) = (r - c)2. (Co+C1r+C2r2), for r ≤ c; =0, for r > c (3)
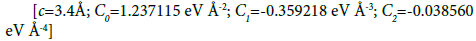
Un the n-body “cohesive function” term can be empirically written as a sum over all atoms
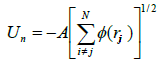 (4)
(4)
Where,
φ(r)= (r-d)2 + β(r-d)3/d r ≤ d = 0 r > d (5)
[A= 1.828905 eV Å-2; d=3.569745 Å; β=1.8]
rij represents the inter-atomic separation between atoms at sites ‘i’ and ‘j’. The functional form was chosen as a square root to mimic the tight-binding theory and the function φ as a sum of overlap integrals. The range ‘d’ in Eq. 5 is a disposable parameter, assumed to lie between the second and third nearest neighbours. Further details on potential parameters used above can be found elsewhere [27].
This potential has been used extensively to study defect properties, elastic behaviour and cohesive properties of iron crystals at zero Kelvin and/or at low temperatures [13,15]. Simulations using this potential are generally carried out in the constant volume NVT ensemble; only small displacements of atoms from their mean position are permitted. This potential has a soft core-core repulsion at small distances that varies as a quadratic polynomial; various atoms could come fairly close when significant atomic movement gets incorporated at high temperatures, especially during simulations in an NPT ensemble.
The Mendelev potential
In the potential developed by Mendelev et al. [19], the energy of an assembly of N atoms is given by
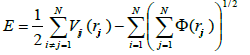 (6).
(6).
Where Vij is the pair-wise repulsive part of the potential and Φ the many body cohesive term of the potential. This potential is divided in three regions. For distances smaller than the nearest neighbour spacing, the atom-atom interactions are described by pair-wise interactions between charged nuclei. Using a ‘universal’ screened coulomb function, the potential can be written as
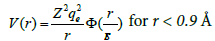 (7)
(7)
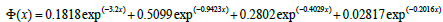 (8)
(8)
where rB is the Bohr radius and Z the atomic number of iron.
For regions r > 1.9 Å, cubic splines were used with a form:
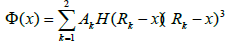 (9)
(9)
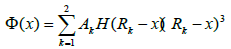 (10)
(10)
Where H is the heavy side step function. Various coefficients are: a1= -36.5598, a2= 62.416, a3= -13.1556, a4= 2.7214, a5= 8.7620, a6= 100.0 in units of eV/Å-3; A1= 72.8683, A2= -100.945 in units of eV/Å-3; r1=1.18, r2=1.15, r3=1.08, r4=0.99, r5=0.93, r6=0.866 in units of Å; R1= 1.3 and R2= 1.2, ao= 2.8665 in units of Å.
For regions between 0.9 and 1.9 Å, a simple interpolation technique was used to ensure the continuity of potential, its first derivative and for a smoothly varying second derivative.
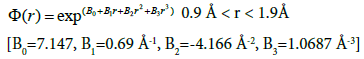 (11)
(11)
Further details on potential parameters used above can be found elsewhere [28,29]. This model potential has been used extensively as an EAM potential. A specific aspect of this model is the Coulomb repulsion between nuclei at small distances (1/r dependence); it therefore is a much harder potential at small distances than the Rosato Potential. Simulations with this potential have generally been carried out in the NVT ensemble; various system parameters in this potential were manually adjusted for simulating high temperature properties. We have used a cut-off distance of 5 Å in this study.
The Sutton Chen potential
This potential was developed as a long-range Finnis-Sinclair potential and has found extensive application in simulating high temperature and high pressure phases of iron under extreme conditions present in the earth’s outer core [22-25]. In this potential, the Finnis- Sinclair component is incorporated through a negative 1/rm tail in the pair potential component. This potential can be written as
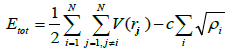 (12)
(12)
Where Etot is the total energy of the system, V(rij) represents the interaction between atoms i and j at a distance rij.
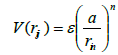
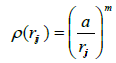 (13)
(13)
The potential was fitted to energy-volume data. The parameters showing the best fit were determined to be: ε = 0.017 306 eV, a = 3.471 392Å, n= 8.137 381, m= 4.7877, c= 24.9390. [21].
This potential is strongly repulsive at small distances (1/r8.137), a key point of difference between the other two potentials used in this study. Secondly, this potential has a very long range (9.5Å); the Rosato potential has a range of only 3.5 Å. Thirdly, computer simulations using this potential have generally been carried out using the NPT ensemble as against the NVT ensemble for the other two potentials. This potential has generally been used to study the behaviour of molten iron under extreme conditions of temperature and pressure [24,25]. Both Rosato and Mendelev potentials have generally been used to investigate the defect behaviour in the solid iron and other system properties [19-21].
Simulation Procedure
Our main focus in this paper is to determine the influence of simulation parameters and the choice of interaction potentials on the onset of structural disorder and the melting transition of iron. No attempt was made to determine the exact melting temperature, which would require the transition to be mapped from the solid as well as the liquid side. It is well known that creating order from disorder is much more difficult and there are significant hysteresis effects associated with such simulations [27]. It is therefore important to identify the optimum potentials and simulation approaches first; investigations on locating the melting point to a high accuracy will be carried out later. The simulation cell was in the form of a BCC lattice with iron atoms placed on the lattice sites. Three lattice sizes, namely, 10×10×10, 12×12×12 and 14×14×14 were used during simulations.
For simulations in the NVT ensemble, the outer boundary of the cell was kept fixed in order to keep the overall volume constant. Atoms located on the boundary were therefore not allowed to move; however these atoms could participate in interactions with neighbouring atoms. Periodic boundary conditions were not used in these simulations. Simulations in the NPT ensemble were carried out in two steps: the volume was kept fixed during simulations in the first step, followed by the periodic changes in the total volume of the simulation cell in the second step. The application of pressure after a number of constant volume runs, allowed for the volume and shape changes to the simulation cell permitting the structure to attain its natural state. Pressure also made contributions to the system energy through a PΔV term, where P is the pressure and ΔV the change in the simulation cell volume. A pressure of 1 atmosphere was used in these studies; the simulation temperature was varied from 600 K to 3000 K.
An atom was chosen at random from the inner simulation lattice; it was allowed one of three possible positional movements: ± ΔX, ± ΔY and ± ΔZ. A number set between 0 and 1 was divided into three equal subsets, which were then allocated to specific atomic movements. A random number η was chosen uniformly between 0 and 1 and directed to the appropriate subset. The deviation of η from the midpoint of the subset, determined the sign and the magnitude of the specific movement. Simulations were carried out with the maximum step size ranging between 0.2 to 0.4 Å. A few simulations were carried out by applying multiple movements to a given atom simultaneously. These however showed a poor convergence with most of the moves becoming energetically unfavourable and were rejected.
The computation of energies was one of the most time consuming part of the simulation algorithm. With the number of atoms in the simulation cell ranging between 2000 and 5488, it required the computation of a very large number of atom-atom distances. Two sets of energy computations were carried out on a selected atom. In the first set, the interacting neighbouring cell of the central atom was visualised as a 3 × 3 lattice surrounding it. All atomic interactions beyond this cell were neglected. In the second set, the size of the interacting cell was increased to 5×5. This increase in the cell size contributed to less than 1% change in energy, but resulted in more than five-fold increase in the simulation time. The contributions from distant neighbours can however become important at high temperatures due to lattice fluctuations and disorder close to melting. The interaction cell was therefore chosen as 5×5, with minor modifications to the algorithm for atoms on the outer boundary. A further increase in the size of the interaction cell was found quite unnecessary at all temperatures.
The range of interaction/cut-off distance was chosen as 3.5 Å for the Rosato potential, 5 Å for the Mendelev potential and 9.5 Å for the Sutton-Chen potential. The ranges were determined from the characteristics of original potentials and were not arbitrarily fixed for these simulations. The energy change ΔE due to the atomic move was calculated. The movement was accepted for ΔE ΔE0. For ΔE > 0, the move could be accepted with a transition probability W
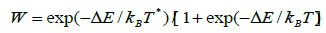 (14)
(14)
where kB and T are respectively the Boltzmann constant and temperature [30,31]. W was compared to a random number η chosen uniformly between 0 and 1. The move was accepted for W >η; otherwise the old configuration was counted once more for averaging. The dynamics of the model consisted of generating a Markovian trajectory through the configuration space. This ‘Kawasaki dynamics’ conserves the concentration of the system and is expected to lead to equilibrium distribution in the limit where the number of states generated tends to infinity. In practice, one expects to achieve fairly accurate results for 106 to 108 MC steps.
A distance fluctuation criterion was used as an order parameter for a quantitative measure of local disorder [32]. The distance dependent Etters-Kaelberer parameter ΔEK can be written as
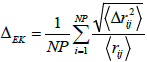 (15)
(15)
Where rij is the distance between atoms i and j, 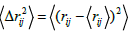 , N the number of particles and NP is the number of neighbouring pairs, where members of each pair are separated by less than the nearest-neighbour cut-off distance. The distance fluctuation parameter is expected to rise very sharply with the onset of structural disorder and melting. The Lindeman criterion of melting is based on the fluctuation of an individual atom relative to its average position [33]. Pair-distribution function and other standard atomic distribution profiles were also computed during simulations. The simulation technique presented here is quite general and can be applied for investigating the melting transition in other metals as well. These simulations can also be extended to incorporate the influence of high pressures along with high temperatures for applications in condensed matter physics as well as in geophysics [34]. Detailed simulation results on three interaction potentials are given in the following section.
, N the number of particles and NP is the number of neighbouring pairs, where members of each pair are separated by less than the nearest-neighbour cut-off distance. The distance fluctuation parameter is expected to rise very sharply with the onset of structural disorder and melting. The Lindeman criterion of melting is based on the fluctuation of an individual atom relative to its average position [33]. Pair-distribution function and other standard atomic distribution profiles were also computed during simulations. The simulation technique presented here is quite general and can be applied for investigating the melting transition in other metals as well. These simulations can also be extended to incorporate the influence of high pressures along with high temperatures for applications in condensed matter physics as well as in geophysics [34]. Detailed simulation results on three interaction potentials are given in the following section.
Results and Discussion
Rosato potential
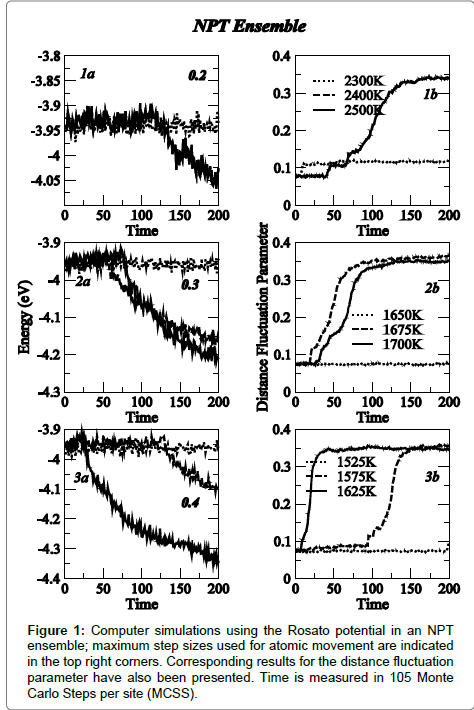
Computer simulation results using the Rosato potential in the NPT ensemble are shown in Figure 1; the variations of energy and distance fluctuation parameter have been plotted as a function of simulation time (measured in units of 105 Monte Carlo Steps per Site). Simulation results have been plotted for a range of step-sizes (0.2 to 0.4 Å) used for atomic displacements during simulations. The onset of structural disorder was marked clearly as a well-defined discontinuous lowering of energy and a corresponding sharp increase in the distance fluctuation parameter. These simulations were carried out on a 10×10×10 BCC iron lattice. The transition temperature was found to depend very sensitively on the step size used, decreasing from 2400K (0.2 Å) to 1575K (0.4 Å). This result is quite surprising as there are no well-defined guidelines in the literature on the choice of MC step-size during similar computer simulations. Generally the choice of an appropriate step size during a move is governed by an adequate acceptance/rejection ratio for the Monte Carlo moves. It is also a common practice to adjust step-sizes during simulations, which can sometimes lead to some undesirable correlations [35]. The main thing to note is the large value of the distance fluctuation factor indicating the onset of melting, an aspect that represents a significant distortion/variation of near neighbour distances. According to the Lindemann criterion [33], distortions of more than 0.1 represent a melted state; we have recorded values of distortion parameter up to 0.4 in these simulations.
Figure 1: Computer simulations using the Rosato potential in an NPT ensemble; maximum step sizes used for atomic movement are indicated in the top right corners. Corresponding results for the distance fluctuation parameter have also been presented. Time is measured in 105 Monte Carlo Steps per site (MCSS).
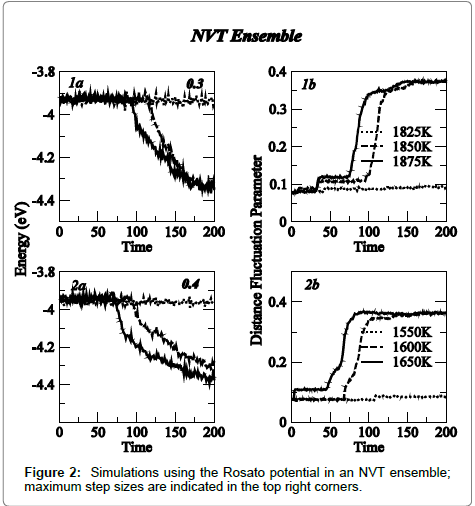
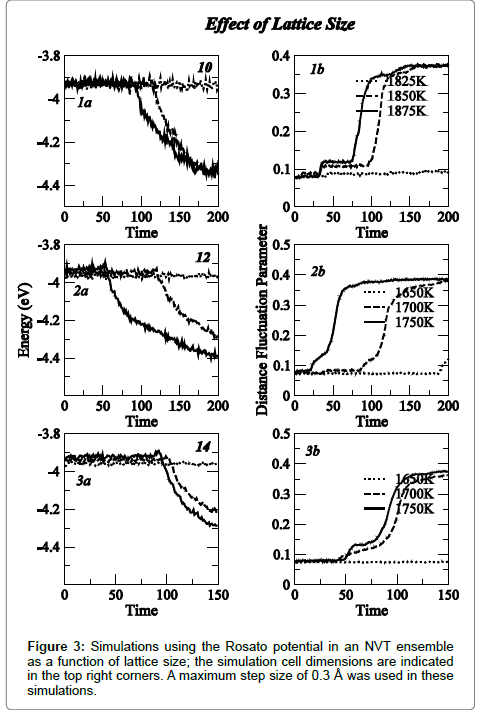
Corresponding results in the NVT ensemble are shown in Figure 2. Transition temperatures of 1850 K (0.3 Å) and 1600 K (0.4 Å) were obtained. It is important to note that periodic boundary conditions were not used in these simulations as these can at-times lead to the sliding of the simulation cell in the configuration space affecting the accuracy of transition temperatures. To overcome/minimise limitations introduced by the boundary conditions, simulations were carried out in the NVT ensemble on larger lattices including 12×12×12 and 14×14×14 lattices with a step size of 0.3 Å. While a small reduction in the transition temperature was obtained with the simulation cell size increasing from 10 to 12, no further change was observed when the lattice size was increased to 14. These results are shown in Figure 3.
Mendelev potential
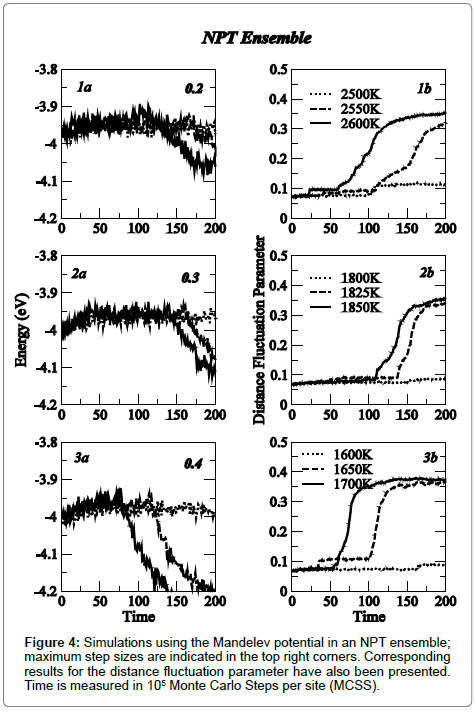
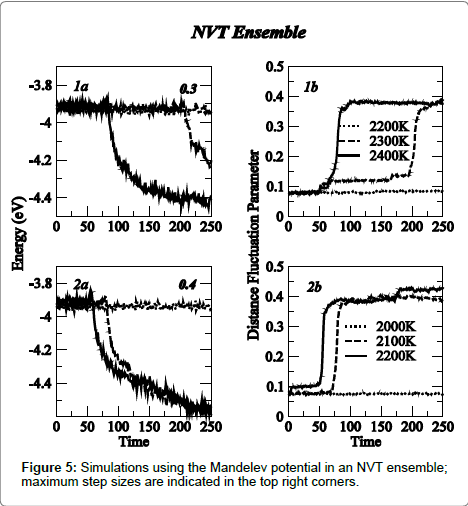
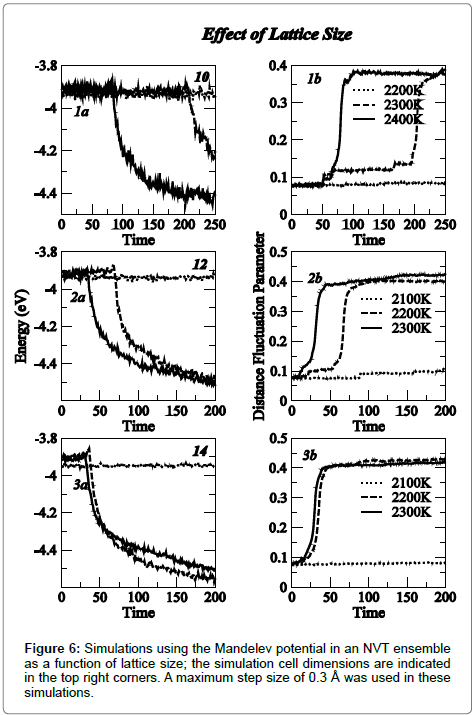
Computer simulation results using the Mendelev potential in the NPT ensemble are shown in Figure 4; the variation of energy and distance fluctuation parameter have been plotted for step-sizes ranging between 0.2 to 0.4 Å. The phase transition was marked clearly as a well-defined reduction in energy and a rapid discontinuous increase in the distance fluctuation parameter. The transition temperature was found to be very sensitive to the step size used, decreasing from 2550 K to 1650 K with the step size increasing from 0.2 to 0.4 Å. These temperatures were consistently higher than those observed for the Rosato potential. Corresponding results for the Mendelev potential in the NVT ensemble are shown in Figure 5. Transition temperatures of 2300 K (0.3 Å) and 2100 K (0.4 Å) were obtained. Simulations in the NVT ensemble were also carried out using 12×12×12 and 14x14x14 lattices with a step size of 0.3 Å. While a small reduction in the transition temperature was obtained with the simulation cell size increasing from 10 to 12, no further change was observed when the lattice size was increased to 14, a trend similar to that observed for the Rosato Potential. These results are shown in Figure 6.
Sutton-Chen potential
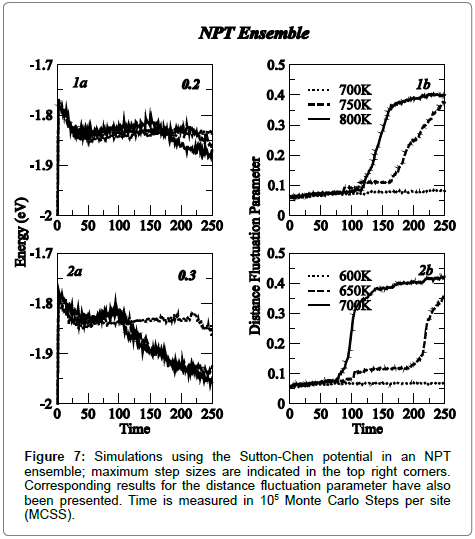
Interaction parameters for the Sutton-Chen potential were determined from investigations on molten iron under extreme conditions of temperature and pressure present in earth’s interior. Simulations were therefore carried out only in the NPT ensemble with the step sizes 0.2 and 0.3 Å. Two key differences were observed (Figure 7). First the energy/atom was found to be significantly higher (~-2 eV), as compared to corresponding energies for the other two potentials ~ -4 eV (typical cohesive energies for iron reported in the literature [16]). Secondly, the melting transition was found to occur at very low temperatures (750 K and 650 K) as compared to the experimental values (~1800K). It is quite likely that these potential parameters need to be modified before their application to atmospheric pressure and lower temperature simulations. Due to significant differences observed, further simulations were not carried out with this potential.
Discussion
Various simulation results have been summarised in Table 1. These include data for the onset of structural disorder and the melting transition of iron using a range of simulation parameters, ensembles, lattice sizes and potentials Up to 2.5 × 107 Monte Carlo steps were used per site in each simulation scenario, as the system is expected to reach equilibrium during these long simulations. The large scatter seen in the simulated results cannot be attributed to inadequate simulation times or lack of equilibrium. The phase transitions in all cases under investigation were clearly marked by discontinuities in energy, along with sharp increases in local disorder and associated transformations of pair-correlation functions. A melting temperature of 2400 K has previously been reported in literature for the Rosato potential [36]. However these authors did not provide sufficient details on simulation parameters. The scatter in results was very high while using the NPT ensemble (1575 K to 2400 K). Increasing the lattice size in the NVT ensemble had a marginal influence on the transition temperature thereby indicating that the absence of periodic boundary conditions did not significantly affect the transition temperature. The results from the Mendelev potential also showed a significant scatter (1650 K to 2550 K) under different conditions.
| No. | Potential Step→ Lattice Size→ |
NPT Ensemble | NVT Ensemble | |||||
|---|---|---|---|---|---|---|---|---|
| 0.4 Å 10 |
0.3 Å 10 |
0.2 Å 10 |
0.4 Å 10 |
0.3 Å 10 |
0.3 Å 12 |
0.3 Å 14 |
||
| 1. | Rosato[17] | 1575 K | 1675 K | 2400 K | 1600 K | 1850 K | 1700 K | 1700 K |
| 2. | Mendelev et al.[19] | 1650 K | 1825 K | 2550 K | 2100 K | 2300 K | 2200 K | 2200 K |
| 3. | Sutton-Chen[22] | _ | 650 K | 750 K | _ | _ | _ | _ |
Table 1: Simulated transition temperatures as a function of MC step size, nature of the ensemble used and lattice sizes for three iron interaction potentials under investigation.
The Sutton-Chen potential showed very low temperatures for the melting transition, which we believe points to the inadequacy of the parameter set used for this temperature/pressure regime. For BCC iron, typical volume associated with every atom is ~12.45 Å3 (lattice parameter: 2.92 Å, close to the melting point); and for molten iron at 6000 K and at 330 GPa in earth’s interior, typical volume associated with every atom is ~6.8 Å [3,25]. The distances involved in those simulations therefore are much shorter and potentials are correspondingly much harder and strongly repulsive. The extension of these potentials for atmospheric pressure simulations could therefore prove to be a non-trivial exercise; and these potentials may not be suitable for these conditions.
A reduction in the size of the MC step, representing smaller atomic displacement during simulations generally resulted in higher transition temperatures. Most of the simulations were carried out for 2x107 Monte Carlo Steps per site, with a typical simulation run using up to 50 hours of CPU time. Such a length of simulation time is adequate in most cases. Extending simulations over even longer times might result in minor improvements. However it is neither practical nor viable to increase processing time much further. Another important observation is regarding significant increases in the distance fluctuation parameters with the onset of local disorder close to melting. These were found to be very sensitive near the phase transformation. In Figure 2, the onset of transition could be seen in the distance fluctuation parameter plot several steps prior to the energy plot. The onset of local disorder/instabilities represents an important precursor to the melting transition. It is possible that the choice of small step size/atomic movements limited the extent of local disorder resulting in a delayed onset of melting.
A number of authors have looked for microscopic precursor mechanisms prior to melting. One of the popular concepts relates to the softening of phonon modes with increasing temperature when atoms no longer possess sufficient restoring force to return to equilibrium positions [36]. The creation/excitation of point defects and dislocations also destroy the periodicity of the lattice. Dislocation lines have also been observed as precursors to melting during Monte Carlo simulations [37]. Bocchetti and Diep [38] have reported on the melting of rare-gas crystals; computer simulations were carried out using Lennard Jones potentials. Simulated melting temperatures have generally been found to be ~13 to 20% higher than the experimental values. The nature of the potential, which should ideally originate from the symmetry of atomic orbitals, can also play an important role; however ab-initio calculations on real system are not yet possible. In the Fe-C phase diagram, the liquidus line depends sensitively on the carbon level varying from 1812 K at zero carbon to low temperature eutectic at 1420 K for 4.3% C. Due to the scatter/ uncertainties observed in the simulated data; a realistic application of computer simulation for steelmaking process would require further developments in the field.
Concluding Remarks
In-depth Monte Carlo simulations were carried out to determine the onset of structural disorder and the melting transition in BCC iron. A range of simulation variables, statistical ensembles and interaction potentials were investigated in a systematic manner. However a large scatter was observed in the simulated results and no welldefined trends or functional dependence could be established. Our results show that two very well-known iron potentials, developed specifically for zero Kelvin applications, clearly showed the melting transition in BCC iron. However a direct correlation could not be established between theory and experiment for quantitative investigations. Iron potentials developed for earth sciences under extremely high pressures/temperatures were not found suitable for steelmaking applications. Further work is therefore required for developing optimum potentials designed specifically for steelmaking applications either by optimising interaction parameters or through developing novel potentials fitted to high temperature properties.
Acknowledgements
Financial support for this research was provided by the Australian Research Council under Discovery Project scheme. Supercomputer support was provided by the National Computing Infrastructure, Canberra and by the Intersect Consortium of New South Wales.
References
- Johnson R (1964) Interstitials and vacancies in α iron. Phys Rev 134: A1329-A1336.
- Osetsky YN, Mikhin A, Serra A (1995) Study of copper precipitates in αâ€Âiron by computer simulation I. Interatomic potentials and properties of Fe and Cu. Philos Mag A 72: 361-381.
- Hasegawa H, Pettifor D (1983) Microscopic theory of the temperature-pressure phase diagram of iron. Phys Rev Lett 50: 130-133.
- Rayne J, Chandrasekhar B (1961) Elastic constants of iron from 4.2 to 300 K. Phys Rev 122: 1714-1716.
- Gao K, Sahajwalla V, Sun H, Wheatley C, Dry R (2000) Influence of sulfur content and temperature on the carbon boil and CO generation in Fe-CS drops. ISIJ Int 40: 301-308.
- Sahajwalla V, Khanna R (2000) A Monte Carlo simulation study of dissolution of graphite in iron-carbon melts. Metall Mater Trans B 31: 1517-1525.
- Sahajwalla V, Khanna R (1999) Influence of sulphur on the solubility of graphite in iron melts: a Monte Carlo simulation study. Acta Mater 47: 793-800.
- Khanna R, Sahajwalla V, Simento N, Seetharaman S (2010) Atomistic Monte Carlo simulations on the influence of sulphur during high-temperature decarburization of molten iron–carbon alloys. Acta Mater 58: 2225-2236.
- Binder K (1997) Applications of Monte Carlo methods to statistical physics. Rep Prog Phys 60: 487-559.
- Khanna R, Sahajwalla V (2013) Atomistic simulations of properties and phenomena at high temperatures. Treatise on Process Metallurgy, Elsevier, Netherlands.
- Batista ER, Heyd J, Henning RG, Uberuaga BP, Martin RL,et al. (2006) Comparison of screened hybrid density functional theory to diffusion Monte Carlo in calculations of total energies of silicon phases and defects. Phys Rev B 74: 1-4.
- Gordon M, Cyrot-Lackmann F, Desjonqueres M (1979) Relaxation and stability of small transition metal particles. Surf Sci 80: 159-164.
- Masuda K, Sato A (1981) Electronic theory for screw dislocation motion in dilute bcc transition metal alloys. Philos Mag A 44: 799-814.
- Foiles S, Adams J (1989) Thermodynamic properties of fcc transition metals as calculated with the embedded-atom method. Phys Rev B 40: 5909-5915.
- Ackland G, Bacon D, Calder A, Harry T (1997) Computer simulation of point defect properties in dilute Fe—Cu alloy using a many-body interatomic potential. Philos Mag A 75: 713-732.
- Finnis M, Sinclair J (1984) A simple empirical N-body potential for transition metals. Philos Mag A 50: 45-55.
- Rosato V (1989) Comparative behavior of carbon in BCC and FCC iron. Acta Metall 37: 2759-2763.
- Baskes M (1992) Modified embedded-atom potentials for cubic materials and impurities. Phys Rev B 46: 2727-2742.
- Mendelev M, Han S, Srolovitz D, Ackland G, Sun D, et al. (2003) Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos Mag 83: 3977-3994.
- Foiles S (1985) Application of the embedded-atom method to liquid transition metals. Phys Rev B 32: 3409-3415.
- Daw MS, Baskes MI (1983) Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals. Phys Rev Lett 50: 1285-1288.
- Sutton A, Chen J (1990) Long-range Finnis–sinclair potentials. Philos Mag Lett 61: 139-146.
- Birch F (1952) Elasticity and constitution of the earth's interior. J Geophys Res 57: 227-286.
- Dziewonski AM, Anderson DL (1981) Preliminary reference Earth model. Phys Earth Planet In 25: 297-356.
- KoÄÂi L, Belonoshko AB, Ahuja R (2007) Molecular dynamics calculation of liquid iron properties and adiabatic temperature gradient in the Earth's outer core. Geophys J Int 168: 890-894.
- Lau TT, Först CJ, Lin X, Gale JD, Yip S, et al. (2007) Many-body potential for point defect clusters in Fe-C alloys. Phys Rev Lett 98: 1-4.
- Marchese M, Jacucci G, Flynn CP (1988) Isotope effect for the vacancy diffusion in bcc alfa-Fe. Phil Mag Letters 57: 25-30.
- Ackland GJ, Bacon DJ, Calder AF, Harry T (1997) Computer simulation of point defect properties in dilute Fe-Cu alloy using a many-body interatomic potential. Phil Mag A 75: 713-732.
- Baskes M (1992) Modified embedded-atom potentials for cubic materials and impurities. Phys Rev B 46: 2727-2742.
- Khanna R, Sahajawalla V (2005) An atomistic model for the graphite–alumina/liquid iron system: Monte Carlo simulations on carbon dissolution.Acta Mater 53: 1205-1214.
- Binder K, Lebowitz JL, Phani MK, Kalos MH (1981) Monte Carlo study of the phase diagrams of binary alloys with face centered cubic lattice structure. Acta Metall 29: 1655-1665.
- Zhou Y, Karplus M, Ball KD, Berry RS (2002) The distance fluctuation criterion for melting: comparison of square-well and Morse potential models for clusters and homopolymers. J Chem Phys 116: 2323-2329.
- Lindemann F (1910) The calculation of molecular vibration frequencies.Physik Z 11: 609-612.
- Errandonea D(2013) High-pressure melting curves of the transition metals Cu, Ni, Pd, and Pt. Phys Rev B 87: 1-5.
- Müller M, Erhart P, Albe K (2007) Analytic bond-order potential for bcc and fcc iron-comparison with established embedded-atom method potentials. J Phys: Condens Matter 19: 20-23.
- Gómez L, Dobry A, Diep H (2001) Monte Carlo simulation of the role of defects as a melting mechanism. Phys Rev B 63: 3-6.
- Gómez L, Dobry A, Geuting C, Diep H, Burakovsky L (2003) Dislocation lines as the precursor of the melting of crystalline solids observed in Monte Carlo simulations. Phys Rev Lett 90: 1-4.
- Bochetti V, Diep HT (2012) Melting of rare-gas crystals: Monte Carlo simulation versus experiments. Cond Matt Stat Phys1-7.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi