Short Communication, J Diagn Tech Biomed Anal Vol: 6 Issue: 1

Physiological Time Series: Analyse and Remove the Drift in 1-2-3

Aasen T^* and Nordahl SHG

College of Applied Medical Sciences, King Saud University, Riyadh, Saudi Arabia

*Corresponding Author : Torbjørn Aasen
National Competence Service for Vestibular Disorders, Department of Otorhinolaryngology, Head and Neck Surgery, Haukeland University Hospital, N-5021 Bergen, Norway
Tel: +47-91750 384
E-mail: torbjorn@aasens.net

Received: October 06, 2016 Accepted: December 20, 2016 Published: January 2, 2017

Citation: Aasen T, Nordahl SHG (2017) Physiological Time Series: Analyse and Remove the Drift in 1-2-3. J Diagn Tech Biomed Anal 6:1. doi: 10.4172/2469-5653.1000117

Abstract

Keywords: Physiological time series; Drift; Symbolic dynamics; Information pattern

Introduction

When analysing physiological data for information pattern, we often face the problem of drift and physiological fluctuations [1].

In this study the consecutive running three data point pattern, with different values (x_i ≠ x_i+1 ≠ x_i+2) in a time series is analysed. Six different patterns are identified. The probability distribution of the pattern from a random time series will be approximately flat, i.e. equally many samples of each pattern (the distribution from an eternally long random time series will be totally flat).

The algorithm is tested on a sequence from the chaotic regime of the logistic map with infinite periodicity,

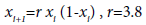
and an optokinetic nystagmus amplitude (OKNA) time series [2-4]. Optokinetic nystagmus is the eye movement reflex elicited by the tracking of a moving field.

Methods

For the purpose of removing drift and testing for short-term information pattern in the time series data the following procedure was applied.

From the time series x_i, find the three points data series w_k , where w_k is

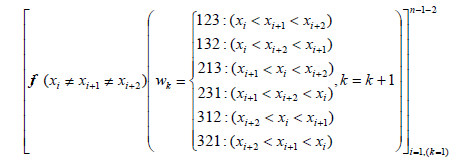
Compute the probability density distribution p_k,

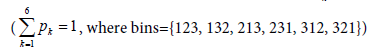
Calculate the normalized information entropy, I, of the probability distribution [3,4,5]

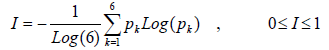
Results

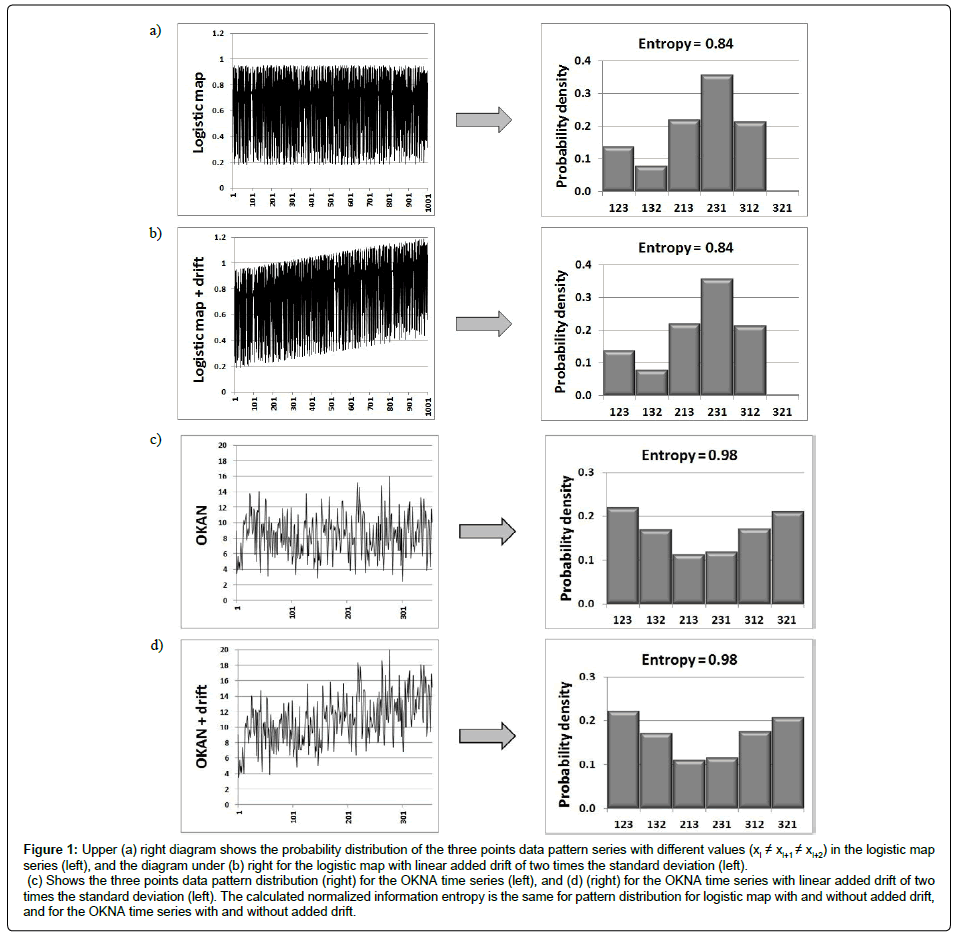
Figure 1 shows the probability distribution, p_k, of the three points data pattern series, w_i, for a) logistic map, b) the logistic map with linear added drift of two times the standard deviation (SD)(n=1000) and for c) OKNAtime series without and d) with linear added drift of two times the SD (n=338). The unequal distribution of the probability distribution shows that some patterns occur more often than others, which indicates information in the data sets. We can see that adding 2*SD drift does not change the pattern distribution or the calculated information entropy, even for the short OKNA time series. The entropy of the pattern distribution for the logistic map without and with added 2*SD drift was calculated to I_LogMap=0.84 and I_OKAN=0.98 for the OKNA time series.

Discussion and Conclusion

The purpose of this study was to test out a simplest possible algorithm to eliminate the effect of drift and detect short-term pattern in physiological data. It has been shown that the method is robust against drifting noise. Adding linear drift of 2*SD did not change the pattern distribution, or the calculated information entropy, for the logistic map or the short OKNA time series.

It remains to see if qualitative information in physiological time series [5] reflects some dynamical properties in the underlying physiological regulating mechanism, that can be detected by this method and substantiate it’s use for diagnostic purposes.

References

1. Song X, Ji T, Wyrwicz AM (2008) Baseline drift and physiological noise removal in high field FMRI data using kernel PCA. Proc IEEE International Conference on Acoustics Speech and Signal Processing 441-444.
2. Magnusson M, Schalén L, Pyykkö I, Enbom H (1998) Clinical considerations concerning horizontal optokinetic nystagmus. Acta Otolaryngol Suppl 455: 53-57.
3. Aasen T, Goplen F, Nordahl SHG (2013) Short-term information pattern in optokinetic nystagmus amplitude time series. J Vestibular Res 23: 71-75.
4. Aasen T (2003) Symbolic dynamics applied to optokinetic nystagmus signals. J Med Eng Techno 27: 145-148.
5. Voss A, Kurths J, Kleiner HJ, Witt A (1996) The application of methods of non-linear dynamics for the improved and predictive recognition of patients threatened by sudden cardiac death. Cardiovasc Res 31: 419-433.