Review Article, J Electr Eng Electron Technol Vol: 14 Issue: 1
Subscribed Power Optimization Using MATLAB, Python, and MS Excel Solver
Younes Lemdaoui1*, Adila Elmaghraoui2, Anass Elyoubi3, Rachid Saadane1, Ahmed Chebak2 and Mohamed El Aroussi1
1 Department of Engineering, Laboratory Engineering System, Hassania School of Public Works, Casablanca, Morocco
2 Department of Engineering, Laboratory Engineering system, Green Tech Institute (GTI) Mohammed VI Polytechnic University, Benguerir, Morocco
3 Department of Engineering, Laboratory Engineering system, National School of Applied Sciences, Agadir, Morocco
*Corresponding Author: Younes Lemdaoui
Department of Engineering, Laboratory Engineering System, Hassania School of Public Works, Casablanca, Morocco
E-mail: ledmaoui.younes.cedoc@ehtp.ac.ma
Received date: 15 August, 2023, Manuscript No. JEEET-23-110356;
Editor assigned date: 17 August, 2023, PreQC No. JEEET-23-110356 (PQ);
Reviewed date: 30 August, 2023, QC No. JEEET-23-110356;
Revised date: 17 January, 2025, Manuscript No. JEEET-23-110356 (R);
Published date: 24 January, 2025, DOI: 10.4172/2325-9833.1000987
Citation: Lemdaou Y, Elmaghraoui A, Elyoubi A, Saadane R, Chebak A, et al. (2025) Subscribed Power Optimization Using MATLAB, Python, and MS Excel Solver. J Electr Eng Electron Technol 14:1.
Abstract
Optimization of subscribed power refers to the process of determining the minimum amount of electrical power that a consumer needs to subscribe to from their energy supplier while ensuring that their electricity demand is met. This involves analyzing the consumer's historical power consumption data, identifying the peak load periods, and implementing load management strategies to reduce peak power demand. By optimizing subscribed power, consumers can reduce their energy costs and contribute to a more efficient and sustainable energy system. This paper proposes three methods to optimize this subscribed power and compares the results between them.
Keywords: Subscribed power; Energy management; Energy saving; Optimization algorithm; Smart grids
Introduction
Introduction Optimizing the contracted power is a key challenge for industries to lower their energy use and costs. The maximum active power algorithm sets a limit on the active power that the industry can use. It keeps track of the active power use and changes the subscribed power, which is the maximum electric power that the company can use at a certain time. This power is in kilovolt-Ampere (kVA). Usually, energy providers offer different levels of subscribed power to suit different businesses. Higher subscribed power levels lead to higher electricity bills, but we also need enough power to prevent blackouts and equipment problems. Optimizing subscribed power is a good way for industrial companies to make their energy use more efficient and save money. Here are some strategies:
Evaluate the power’s need: The first thing to do is to evaluate how much power your company needs, including checking how much each device uses and looking at your energy use patterns.
Using tools for energy management: Use tools for energy management: Using tools like monitoring and control systems can help you see how much energy you use in real time and find ways to save energy.
Reduce energy consumption: Reducing energy consumption energy like using devices that use less energy and avoiding waste. Enhanced production planning can result in reduced energy usage and optimized subscribed power.
Pick the right subscribed power: Picking the right subscribed power is important to prevent fines and extra costs for going over the limit. Companies should pick enough power to run their devices, but not too much that could make them pay more than they need to.
Energy consumption monitoring: It is important for companies to strike the right balance between the capacity needed to meet their power needs and the amount of excess capacity that can incur additional costs due to the subscribed power overrun fee which is a financial penalty that companies must pay if they exceed their contractual subscribed power during a given period. This penalty is generally charged by the electricity companies and is calculated according to the amount of excess energy consumed beyond the contracted power.
The amount of the overage charge may vary depending on several factors, such as the rate of overage, the duration of the overage, the season of the year and the prevailing tariff rates. In some cases, companies may also be subject to additional penalties for peaks in demand or for unauthorized use of excess power.
To avoid oversubscription charges, companies can adopt energy efficiency practices, such as implementing demand management programs, optimizing production schedules, using energy-efficient equipment, energy and real-time energy consumption monitoring [1]. In addition, companies can adjust their subscribed power according to their energy needs, so that their energy consumption remains below their contractual limit.
Machine learning has the capability to optimize consumption patterns effectively. By harnessing advanced algorithms and data analysis techniques machine learning can discern intricate patterns and correlations within consumption data. This enables the identification of optimal usage scenarios, leading to more efficient resource allocation and utilization. Whether it's energy, materials, or other resources, machine learning's ability to adapt and learn from patterns over time empowers industries to make informed decisions, minimize waste, and achieve higher levels of sustainability and costeffectiveness in their consumption practices [2].
Moreover, the power charge is a component of the electricity tariffs which is invoiced to customers according to the electrical power they have subscribed to. It aims to encourage customers to subscribe to the power they need and to reflect the fixed costs associated with the construction and maintenance of electrical infrastructure.
In summary, the charge for exceeding subscribed power is a financial penalty that companies can avoid by implementing energy efficiency practices and adjusting their subscribed power according to their energy needs.
Problematic: The problematic of optimizing subscribed power is to reduce energy consumption and the associated costs in industrial environments. The choice of subscribed power is crucial to avoid unnecessary costs and overage penalties. It is important to choose sufficient power to avoid power interruptions and equipment failures while avoiding subscribing too much power and incurring unnecessary additional cost.
Objective: The objectives of optimizing subscribed power are to maximize the energy consumption efficiency of companies and reduce costs. This can be achieved by evaluating the energy needs of the company, using energy management tools to monitor and control energy consumption in real-time, implementing energy-saving practices such as using energy-efficient equipment, reducing waste, optimizing production schedules, and choosing the right subscribed power to avoid unnecessary costs and overage penalties. Another objective of optimizing power subscriptions is to become more sustainable. By reducing energy consumption, businesses can reduce their carbon footprint and help protect the environment. Furthermore, it can also help businesses improve their performance.
Literature Review
Related works
Optimization of subscribed electrical power has been a significant focus in recent years. One of the key aspects of subscribed power optimization is to optimize the subscribed power level based on historical data and future predictions. A study conducted by Alcayde et al., proposed a methodology to determine the value of the contracted electric power for an annual period of a standard highvoltage multi-period tariff for different time periods. The methodology uses genetic algorithms to optimize the tariff selection and minimize electricity costs, including the cost of power contracted and heavy penalties for excess power demand over the power contracted in certain time periods. This research provides valuable insights into how genetic algorithms can be used to optimize electricity tariffs, which is similar to subscribed power optimization that aims to optimize subscribed power levels. By using historical data and future predictions, both methods aim to reduce electricity costs and improve energy efficiency by optimizing the use of electricity [3].
In their comprehensive reference book, editors Fred Glover and Gary Kochenberger offer valuable insights into the theory, algorithms, and applications of various metaheuristic methods for optimization problems. This work is particularly relevant to our study of subscribed power optimization, as it covers a wide range of metaheuristic algorithms, including simulated annealing, genetic algorithms, tabu search, ant colony optimization, and particle swarm optimization. These methods have demonstrated success in addressing complex realworld optimization problems, such as scheduling, routing, machine learning, and data mining.
The Handbook of Heuristics, serves as a valuable resource for our research on subscribed power optimization [4]. The book delves into various aspects of heuristics, problem-solving methods that prioritize practicality and efficiency, albeit without a guarantee of finding the optimal solution. With its extensive coverage of classic and modern heuristics, meta-heuristics, exact and hybrid methods, as well as heuristics for specific application areas and problem types, this handbook presents a plethora of techniques that could be applied to subscribe power optimization. Furthermore, the book's section on experimental design and analysis offers valuable guidance on designing experiments to evaluate heuristics and analyze the results, which is essential for assessing the effectiveness of the proposed methods in the context of subscribed power optimization.
In search optimization, genetic algorithms can be used to find optimal solutions to problems that have many possible solutions, such as finding the shortest path between two points in a complex network. They can also be used to optimize complex mathematical functions, such as those used in financial modeling and engineering design [5].
Community detection in power grids is another essential aspect of power systems engineering. An article by Martí et al., involved the application of genetic algorithms to detect communities in national-scale high voltage transmission networks [6]. The genetic algorithms are guided by the modularity index and consider different levels of detail in the grid. The article presents two genetic algorithms, namely NSGA-II and SPEA2, which are used to solve the community detection problem in graphs. An empirical study is conducted to compare the performance of these methods in detecting communities in five national-scale grids, including Italy, Germany, France, the Iberian peninsula (Spain and Portugal), Texas (US), and the IEEE 118 bus test case that represents a portion of the American Electric Power System (in the Midwestern US). The results show that genetic algorithms can effectively detect communities in power grids and provide useful information for vulnerability risk analysis to avoid large-scale cascade failures. Furthermore, the use of genetic algorithms in community detection has shown promising results in terms of computational efficiency and accuracy. The approach presented in this article is particularly relevant for power systems engineering, where the identification of communities can provide valuable insights into the behavior and vulnerabilities of the grid. The study also highlights the importance of considering different levels of detail when analyzing large-scale systems, as this can significantly impact the quality and usefulness of the results. Overall, this work contributes to advancing our understanding of complex networks and provides a framework for future research in community detection and vulnerability analysis in power systems engineering.
Research in non-sinusoidal circuits has focused on minimizing harmonic disturbances using filters. A study by employed geometric algebra theory and evolutionary algorithms to develop a new approach for designing passive filters that can maximize power factor compensation in non-sinusoidal circuits. This study built upon previous works that used particle swarm optimization and hybrid algorithms combining genetic algorithms and simulated annealing for filter design and parameter optimization [7]. There has been significant research in recent years on the use of filters to minimize harmonic disturbances in non-sinusoidal circuits. Some researchers have focused on developing new filter designs that can better handle the complex behavior of these circuits, while others have explored optimization techniques for finding the best filter parameters. For example, one recent study used particle swarm optimization to design a passive filter for a three-phase system, while another study used a hybrid algorithm combining genetic algorithms and simulated annealing to optimize the parameters of an active filter. The present article builds on this previous work by using geometric algebra theory and evolutionary algorithms to develop a new approach for designing passive filters that can maximize power factor compensation in nonsinusoidal circuits.
In the context of electricity consumption management, a study conducted at the eastern container terminal at the port of Casablanca provided a comprehensive methodology for analyzing and optimizing electrical energy consumption in industrial settings [8]. The study highlights the importance of managing and reducing electricity costs as a means of improving competitiveness for businesses. The methodology involves analyzing the terms of the electricity supply contract, monitoring overall consumption, and implementing solutions to optimize consumption and improve electrical power. These solutions include techniques such as electrical counting at the head of the loop, optimizing subscribed power, managing time slots, improving power factor through reactive energy compensation and harmonic filtering, improving lighting energy efficiency, and sizing photovoltaic panels for partial coverage of needs [9]. The study also involves conducting a diagnostic analysis to identify areas for improvement and making recommendations based on the findings. Overall, this study offers practical solutions that can be applied in a variety of industrial settings to reduce costs and improve competitiveness.
Methodology
Solver sipmlex
• In most real problems, there are more than two variables to be determined.The simplex method is an algebraic procedure for solving linear programs with more than two variables.
• It is an exact and iterative method in which we find the concepts seen in graphical resolution. The general form of a linear programming model is: Max (or min) z = c1x1 + • • • + cnxn Under the constraints:
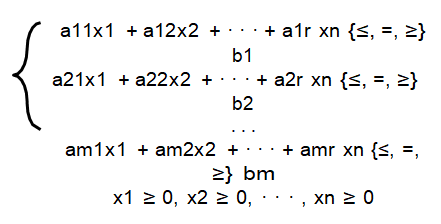
To make all the steps of the simplex algorithm systematic, they can be organized in the form of tables. In our example, the initial Tables 1 and 2:
| X1 | X2 | S1 | S2 | s.m. | v.d.b. |
|---|---|---|---|---|---|
| 1 | 2 | 1 | 0 | 21 | S1 |
| 2 | 2 | 0 | 1 | 24 | S2 |
| 3 | 4↑ | 0 | 0 | 0 | -Z |
Table 1: Initial table of simplex algorithm.
| X1 | X2 | S1 | S2 | s.m. | v.d.b. |
| 0 | 1 | 1 | 1 | 9 | X2 |
| 1 | 0 | 1 | 2 | 3 | X1 |
| 0 | 0 | 1 | 2 | 45 | -Z |
Table 2: Final table of simplex.
After some iterations of calculation, we find an optimal value z=45:
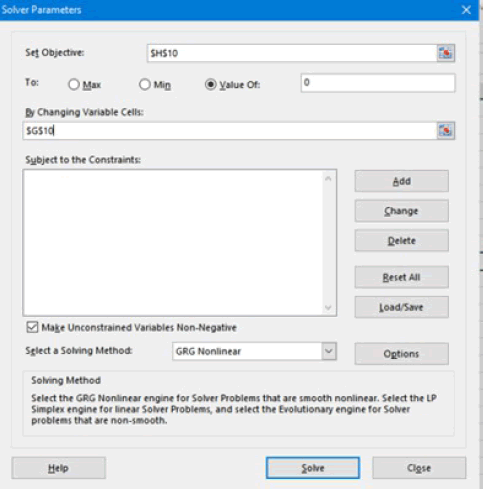
Using MS Excel solver
To solve an equation in Excel, we use the solver option. The solver option allows us to identify the roots of an equation, i.e., the values of x for which a given equation is zero.
Initially, we determine the objective to be defined, which is the solution of at x=0, and then we fill in the value of x in the variable cell box, and finally we click on solve to obtain the result (Figure 1).
MATLAB
MATLAB is software that allows for numerical simulations based on numerical analysis algorithms [10]. It can therefore be used for the approximate solution of differential equations, partial differential equations or linear systems, complex numbers, manipulation of values, matrix operations, polynomial operations, symbolic computation, etc., and also graphics.
To program a MATLAB function, it must be declared in a new script, and then saved, and finally, the function is called.
• We can also have several outputs.
• For nonlinear systems, we use the function “fsolve” with the following syntax: {fsolve=@the_function,initial_value}
Python
There are several optimization algorithms available in Python. One popular library for optimization is SciPy, which provides several commonly used optimization algorithms through its SciPy. Optimize package. Another library is optimization-algorithms, which contains useful algorithms for several complex problems such as partitioning, floor planning, and scheduling. A Google developer also provides a guide on how to set up an optimization problem using OR-Tools for Python.
Optimization-algorithms are a Python library that contains useful algorithms for several complex problems such as partitioning, floor planning, and scheduling. This library provides many implementations for many optimization algorithms. The library is organized in a problem-wise structure. For example, there are many problems such as graph partitioning problem, scheduling problem, etc. For each problem, there are many algorithms to solve it. For each algorithm, there are many possible approaches to implement it.
Digital tools
Solver: The simplex method: MS Excel solver is an add-in tool for Microsoft Excel that allows users to perform optimization and simulation tasks. The MS Excel version used in this paper is 2019; the solver extension can be used to find the optimal solution to a problem by changing the values of certain variables within a set of constraints. Solver can handle linear and nonlinear programming problems, as well as problems with integer constraints. It is commonly used for tasks such as resource allocation, production scheduling, and financial planning.
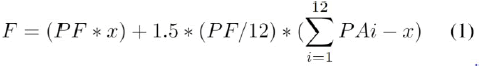
We made the function F which represents the sum of the royalties and the overage of the subscribed power represented by x that is our target variable:
MATLAB: Script: This is a MATLAB script that defines a function named func2(). The script contains several lines of code that calculate an optimized subscribed power value based on input parameters.
The script outputs the optimized subscribed power value using the disp() function.

Python script: This is a Python code block that contains a for loop that iterates over a range of values between min and max. Within the loop, the code calculates an objective value based on the input parameters and appends it to a to a new list. After the loop completes, the code finds the minimum tuple value in the new list using the min() function and assigns it to the result variable.
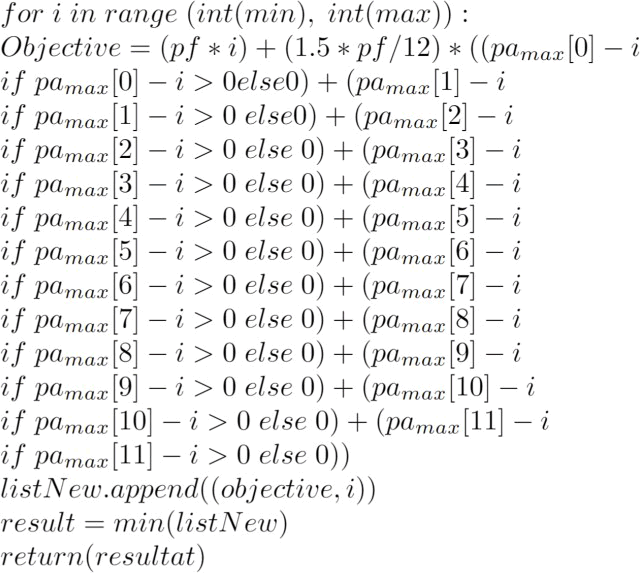
Results and Discussion
We took the case of a factory in Morocco, we took the bills of the last three years to apply the three methods and optimize their subscribed power, the following table illustrates the subscribed power over the years, the power factor as well as the maximum power drawn by the factory.
Tables 3 and 4 and Figures 2-4 illustrate the results obtained using the three methods. Data of an example of an industrial factory for 3 years (Tables 5 and 6).
| MT general | Subscribed power | Power factor | MAX power | |
|---|---|---|---|---|
| KVA | KVA | |||
| 2020 | January | 1200 | 1 | 78 |
| February | 1200 | 1 | 72 | |
| March | 1200 | 1 | 99 | |
| April | 1200 | 1 | 113 | |
| May | 1200 | 0.999 | 104 | |
| June | 1200 | 0.999 | 87 | |
| July | 1200 | 0.969 | 90 | |
| August | 1200 | 0.891 | 77 | |
| September | 1200 | 0.892 | 83 | |
| October | 1200 | 0.96 | 84 | |
| November | 1200 | 0.97 | 89 | |
| December | 1200 | 0.93 | 109 | |
| 2021 | January | 1200 | 0.999 | 104 |
| February | 1200 | 0.999 | 88 | |
| March | 1200 | 0.999 | 82 | |
| April | 1200 | 0.999 | 89 | |
| May | 1200 | 0.999 | 82 | |
| June | 1200 | 0.999 | 61 | |
| July | 1200 | 0.999 | 181 | |
| August | 1200 | 0.999 | 217 | |
| September | 1200 | 0.999 | 89 | |
| October | 250 | 0.999 | 72 | |
| November | 250 | 0.999 | 96 | |
| December | 250 | 0.999 | 237 | |
| 2022 | January | 250 | 0.999 | 237 |
| February | 250 | 0.999 | 245 | |
| March | 250 | 0.999 | 172 | |
| April | 250 | 0.999 | 132 | |
| May | 250 | 0.974 | 186 | |
| June | 250 | 0.954 | 219 | |
| July | 250 | 0.944 | 244 | |
| August | 250 | 0.944 | 219 | |
| September | 250 | 0.952 | 144 | |
| October | 250 | 0.959 | 128 | |
| November | 250 | 0.979 | 108 | |
| December | 250 | 0.991 | 101 | |
Table 3: Industrial factory power data for three years.
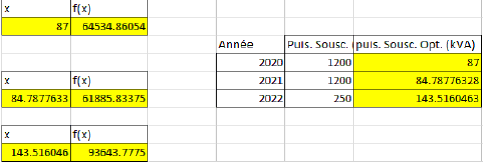
MS Excel solver: Results for three years.
MATLAB results for the three years.
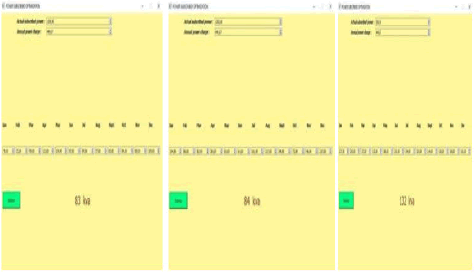
Python results for the three years.
Optimized subscribed power summary.
| Year | Solver | MATLAB | Python |
|---|---|---|---|
| 2020 | 87 | 83.98 | 83 |
| 2021 | 84.79 | 84.6 | 84 |
| 2022 | 143.52 | 144 | 132 |
Table 4: optimized subscribed power summary table.
| Year | Solver | MATLAB | Python |
|---|---|---|---|
| 2020 | 43730.41 | 43561.78 | 43561.78 |
| 2021 | 61885.83 | 61885.83 | 61885.83 |
| 2022 | 93643.78 | 93643.78 | 93643.78 |
| Optimized subscribed power | 199260 | 199091.4 | 199091.4 |
| Previous subscribed power | 1191626 | 1191626 | 1191626 |
| Gain | 992365.5 | 992534.1 | 992534.1 |
Table 5: Gain for the three algorithms (MAD)
The objective of this paper is to minimize the total cost of energy consumption while ensuring a reliable supply of electricity. The equation considers the cost of purchasing electricity from an external supplier, as well as the cost of un-served energy, which includes the direct costs of downtime as well as any lost revenue or productivity resulting from an outage.
The variables in this equation can be adjusted to reflect the specific needs and constraints of each business. For example, the probability of an un-served energy event can be based on historical outage data or estimated based on the reliability of the local power grid.
By using this equation to optimize power subscription, businesses can make informed decisions about their energy consumption and ensure that they are getting the best value for their money while maintaining a reliable supply of electricity.
After subscribed power optimization, the optimal result is that of python and MATLAB because it generates a gain of 992534.1075 MAD, which is better than 992365.4812 MAD, this application can be used in order to adjust power subscribed according to the needs of the consumer.
Conclusion
In conclusion, optimizing the subscribed power is a crucial task for many industries to reduce their energy costs and avoid costly penalties. In fact, by accurately estimating energy consumption, identifying opportunities for energy efficiency, and taking advantage of new energy technologies, businesses can choose the right power subscription plan and better manage their energy costs. Moreover, by choosing the right level of power subscription, industries can save money on their energy bills. In this paper, we have demonstrated the use of powerful tools such as MS Excel solver, MATLAB, and Python to achieve this goal. These tools provide flexible and effective methods for finding the optimal level of power subscription.
By building on our past work and continuing to innovate, we hope to help industries make more informed decisions about their energy usage. By choosing the right level of power subscription, industries can save money and reduce their environmental impact. We believe that our work has the potential to make a significant contribution to this important goal.
In future work, we aim to connect a smart meter to the python application to automate the collection of data and notify the consumer with the optimal subscribed power that allows him to have financial gains.
References
- El Maghraoui A, Ledmaoui Y, Laayati O, El Hadraoui H, Chebak A (2022) Smart energy management: A comparative study of energy consumption forecasting algorithms for an experimental open-pit mine. Energies 15: 4569.
- Ledmaoui Y, El Maghraoui A, El Aroussi M, Saadane R, Chebak A, et al., (2023) Forecasting solar energy production: A comparative study of machine learning algorithms. Energy Rep 10: 1004-1012.
[Crossref]
- Ledmaoui Y, Maghraoui AE, Chebak A (2022) Solar charging station for electric vehicles with IoT solution for monitoring energy production. In International Conference on Smart Applications and Data Analysis, 63-77.
- Alcayde A, Banos R, Arrabal-Campos FM, Montoya FG (2019) Optimization of the contracted electric power by means of genetic algorithms. Energies 12: 1270.
- Glover FW, Kochenberger GA (2006) Handbook of Metaheuristics. Springer Science and Business Media; Berlin, Germany.
- Marti R, Pardalos PM, Resende MG (2018) Handbook of Heuristics. Springer International Publishing; Berlin/Heidelberg, Germany.
- Goldberg DE (2006) Genetic algorithms. Pearson Education India; Chennai, India.
- Guerrero M, Montoya FG, Banos R, Alcayde A, Gil C (2018) Community detection in national-scale high voltage transmission networks using genetic algorithms. Adv Eng Inform 38: 232-241.
- Montoya FG, Alcayde A, Arrabal Campos FM, Banos R (2019) Quadrature current compensation in non-sinusoidal circuits using geometric algebra and evolutionary algorithms. Energies 12: 692.
- El Hafidi A (2014) Optimization of electricity consumption of the eastern container terminal at the port of Casablanca.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi