Research Article, J Ind Electron Appl Vol: 1 Issue: 1
An Active AC Grid to DC Microgrid Interface Using a Bidirectional Bridgeless Flyback Converter
Pablo J. Quintana-Barcia*, Jorge Garcia, Manuel Rico-Secades and Emilio L. Corominas
University of Oviedo, Department of Electrical, Electronic, Computers and Systems Engineering, Spain
*Corresponding Author : Pablo J. Quintana-Barcia
University of Oviedo, Department of Electrical, Electronic, Computers and Systems Engineering, Spain
Tel: +34-606547549
E-mail: quintanabarcia.pablo@gmail.com
Received: June 25, 2017 Accepted: September 16, 2017 Published: October 01, 2017
Citation: Quintana-Barcia PJ, Garcia J, Rico-Secades M, Corominas EL (2017) An Active AC Grid to DC Microgrid Interface Using a Bidirectional Bridgeless Flyback Converter. J Ind Electron Appl 1:1.
Abstract
The usage of power electronics in power systems is one of the key techniques for boosting the development of microgrids. Particularly, in the case of public lighting systems, power electronics converters are applied to both the LED driving stage and the grid interfacing stage. From the point of view of the grid, the latter stage usually behaves as a high power factor (PF) load. However, recent trends in these systems imply a manifold of different storage and renewable energy microgeneration units connected to the DC bus of each street lamp. All together are usually known as lighting smartgrids. The present work aims for keeping the DC bus stable, injecting or extracting energy whereas maintaining high PF with respect to the AC grid. This idea is performed by means of a power droop control that provides the current reference to the grid-tie power converter: a bidirectional bridgeless discontinuous conduction mode (DCM) Flyback converter. This paper defines, explains and implements a power droop control as well as a novel unified switching pattern for the bidirectional DCM Flyback converter, suitable for both inverter and rectifier operating modes. Another contribution is that the proposed switching pattern enables for a smooth transition between these modes. The proposed strategy provides the pulses for every switch at the interfacing stage in the adequate sequence, thus simplifying the design and implementation of the power and control stages. The proposed switching pattern is validated through experimental results.
Keywords: Bidirectional converters; Distributed power generation; Droop control; Flyback Converter; Grid-tie Inverter; Power Electronics; Power Factor Correctioln
Abbreviations
DCM: Discontinuous Conduction Mode; DG: Distributed Generation; ESS: Energy Storage System; HF: High Frequency; PF: Power Factor; PFC: Power Factor Corrector; PV: Photovoltaic; PWM: Pulse Width Modulation; RES: Renewable Energy Source; SLS: Street Lighting System; THD: Total Harmonic Distortion
Introduction
The strong energy dependence on fossil fuels, the negative effects of global warming related to greenhouse gases as well as growing social concern about negative effects of pollutant emissions have led some governments to promote the integration and use of Renewable Energy Sources (RES) [1-4]. PV and wind energy are gaining more and more visibility at small-scale applications. Stand-alone systems where the access to the grid is not available have been making use of these kind of technologies for many years, but, on the other hand, when a RES is connected to the mains, some concerns must be taken into account: harmonic content of the injected current, galvanic isolation or islanding detection among other issues [5-7]. Generally speaking, it can be assumed that the grid is able to absorb certain amount of energy and behave as sort of an energy storage subsystem. However, it is true that this is a rather simplistic view and correct only if a small number of RES units are connected. If many renewable generators are linked to the grid, it does not operate anymore as a battery with an ideal unlimited storage capacity [8-11]. Multifunctional systems that combine a lamp for street lighting and a RES unit for energy injection in the grid are becoming very interesting solutions since they can reduce the budget assigned to public lighting by local governments and help to prevent greenhouse effect [2,12,13].
Power electronics applied to power systems are required to achieve these objectives. A manifold of different power injection topologies have already been studied and are extensively reported in the technical literature [5,13-20]. Most of the power inverter stages consist in an H-bridge converter due to its modularity, high reliability, good performance and low cost [16]. However, the DC bus voltage in such topology must have a higher value than the peak value of the mains voltage in order to be able to inject current into the grid. Alternatively, this condition might be fulfilled by including a bulky step-up LF transformer which would increase cost and size of the stage. However, this option can be discarded by using a single bidirectional DC-AC stage that includes a HF transformer. One alternative for this operation scheme is the combination of an H-bridge and a Dual Active Bridge (DAB) [21,22]. This power conversion stage makes use of at least 12 transistors but, on the other hand, high power density and good efficiencies can be achieved. For power levels below 300W, the Flyback converter is a suitable solution, providing the required voltage mismatch adaptation between terminals [23-25]. One constraint that prevents the use of this topology for higher power values is the stress levels required in the switches, mainly due the leakage inductance of the transformer [13,15,26-28]. Also, another drawback is the fact that it uses the core less efficiently than other topologies, what means that the benefits in size, weight and cost are present only for small power levels. However, this optimal power range of the DCM Flyback is expected to be extended beyond these limits due the recent technology advancements in power electronic devices (reduced onstate resistance, higher avalanche energy strength, greater frequency ratios) as well as in reactive elements design (new magnetic core materials with lower losses and higher frequency operative ranges).
A variation of this topology can be used as an input PFC converter as well as a high-frequency inverter. Different studies of both operating modes but working independently can be found in the literature [13,15,17,18,20,26-28]. Particularly, the present paper is the extension of two previous works: [13,14] where the operation of the bidirectional Flyback converter without swift operating mode changes was shown. Hence, it worked as an inverter during the day, injecting the power generated by a PV panel into the AC mains, and as a PFC during the night providing enough energy to light the lamp. There was no smooth transition between both modes and each one had its own different control strategy.
Nevertheless, this previous strategy is not suitable if the hybrid lighting system includes a RES that can operate all day long. Transitions among rectifier and inverter modes must be done promptly avoiding undesirable transients. This is especially necessary for power electronic converters applied to the actual power systems [29,30]. The particular contribution of this paper is to propose, implement and test a unified PWM switching strategy of the bidirectional Flyback converter in DCM, valid for both power flow directions: from the grid to the DC bus (rectifier mode) and vice-versa (inverter mode). Moreover, the DC bus has to be kept stable within a certain voltage range. Hence, the current reference for the power converter is calculated based on a droop strategy that relates the DC bus voltage with the instantaneous available power. A primitive idea was previously presented by the authors in [31]. However, that work lacked of evidences of the transition among modes and deeper technical analysis included in the present paper. Also, extended experimental results to demonstrate the feasibility of the proposed solution operating as a DC bus stabilizer based on a droop control are presented in this work.
This paper is organized as follows: First, the role of the power stage under study is discussed. Then, the switching pattern for the transistors is explained in detail. Afterwards, a discussion of the experimental results is carried out to demonstrate the proposed control scheme. Finally, conclusions and future developments are exposed.
The Role of Power Stage Under Consideration
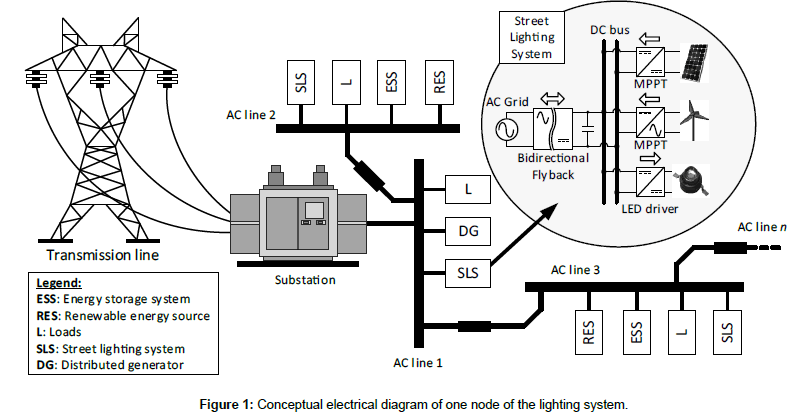
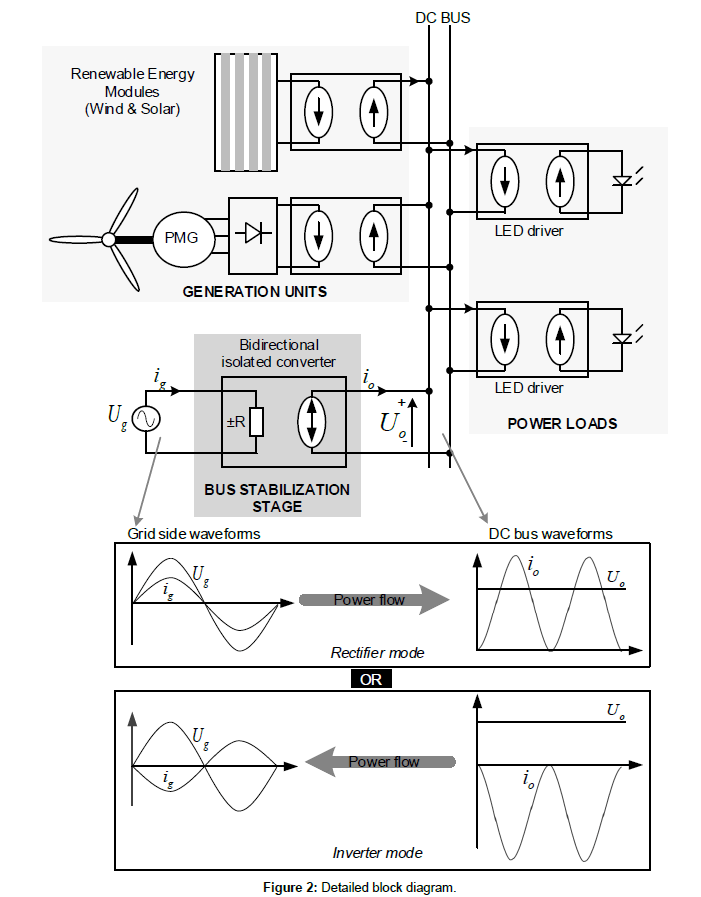
Figure 1 depicts the basic scheme of a generic AC power system, from the transmission line to the final consumers. A number of different resources and loads are interfaced with the AC grid. These resources include Energy Storage Systems (ESS), Distributed Generators (DG) (including RES), loads and finally the street lighting system under consideration. A more specific circuit diagram of each lighting node is shown in Figure 2 with PV and micro wind turbine (μWT) generators, the lamp and the proposed interfacing converter. Dedicated power electronic stages interconnect these subsystems in the lighting node with the DC link. This work offers an easy solution to derive a low power DC microgrid suitable for different applications from the AC grid. In this case, this idea was applied to a hybrid street lighting.
The generation units (RES) have a unidirectional behavior. They extract energy from the energy source through an MPPT and inject it into the DC bus. Similarly, the lamps are also unidirectional, i.e., they extract energy from the DC bus according to their requirements. This situation can cause unbalances in the DC bus so it is required a key element in the microgrid: a grid-tie bidirectional converter has to assume the role of keeping the whole system balanced under every possible situation. In addition, this grid-tie converter must comply with the grid requirements imposed by the regulation and directives, preserving high PF with the AC grid.
As mentioned, the H-bridge is a good solution. It can switch automatically and smoothly from rectifier operation to inverter and vice-versa, yielding low Total Harmonic Distortion (THD) and high PF. Nevertheless, unlike the bidirectional AC-DC Flyback converter, it does not provide galvanic insulation or a more compact design [13,14]. This topology can operate as an input PFC converter as well as a High Frequency (HF) inverter. For instance, it will be initially considered the operation of the system at night. If the μWT is not providing power, then the bidirectional Flyback operates as a PFC taking energy from the grid. If the μWT generates some power, the DC bus voltage level increases and the control system must decrease the power demanded from the AC mains. At a given point, the power drained from the μWT can be greater than the power required by the lamp. Hence, the control must send this extra power back to the utility grid. Under these conditions, the Flyback converter must work as a controlled inverter. Furthermore, this change must be soft and swift ensuring the DCM condition is kept within the transition.
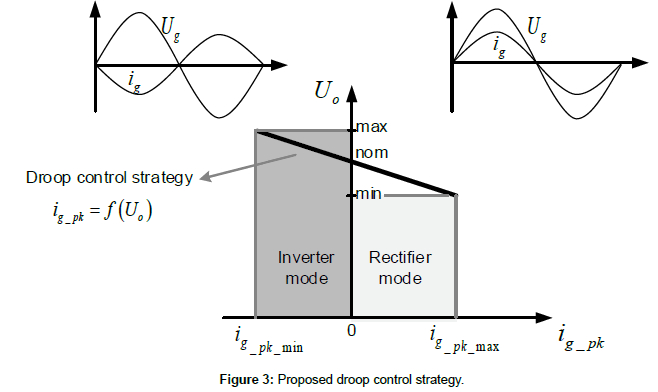
The scope of this paper is to properly control the proposed bidirectional isolated Flyback converter operating as a DC bus stabilization stage (Figure 2). The proposed solution combines the advantages of PFC solutions with droop control strategies in DC smart grid contexts. Then, the proposed droop control strategy shown in Figure 3 allows modifying the peak grid current and its sign according to the DC bus voltage keeping a high PF. For all practical purposes therefore, the proposed solution implies that the power injected or extracted from the DC bus linearly depends on its voltage (Power Droop Control).
Methodology of the Switching Scheme of the Converter
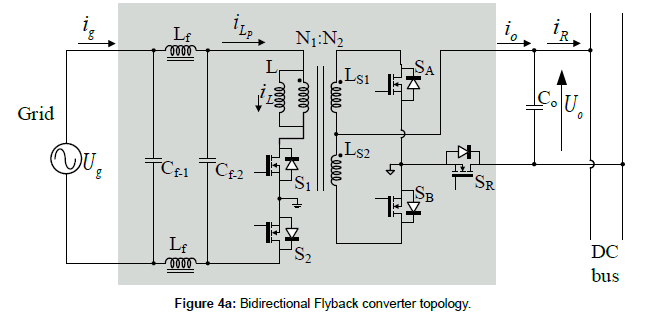
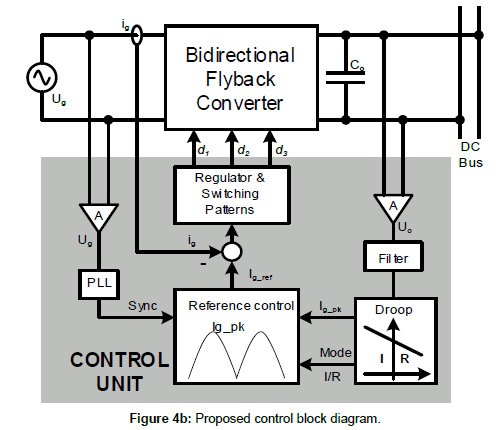
The considered bidirectional Flyback topology is represented in Figure 4a. Additionally, the block diagram that explains how to achieve the previously mentioned droop control can be found in Figure 4b. The switching sequences of every switch in the topology, for both rectifier and inverter modes operating independently are deeply explained in [13,34]. However, the stochastic nature of RES compels to define a unified switching pattern valid for both operating modes in order to change from one to the other swiftly. The following considerations do need to be kept in mind:
• DCM operation is preserved at any time and thus the magnetizing inductor has to be discharged in every switching period.
• The converter is working in steady state. All parameter’s instantaneous value is repeated each switching time, T.
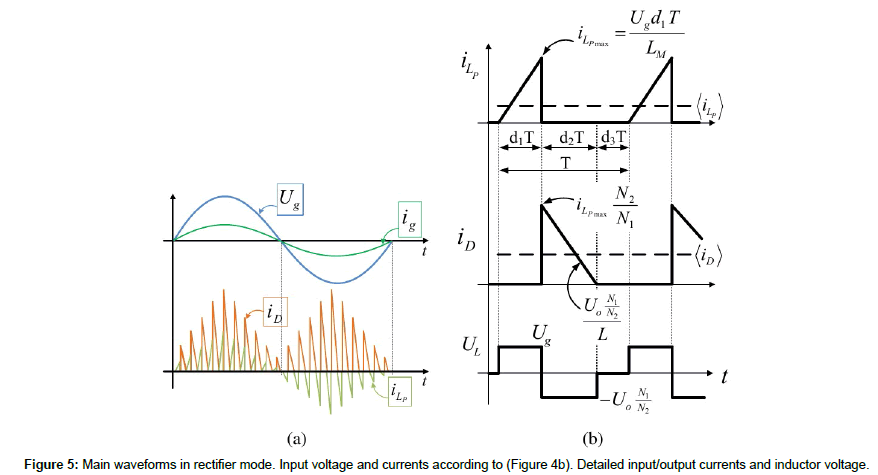
In order to ensure DCM operation of the input stage, the current waveforms in the Flyback inductor, for every operation mode, will be analyzed. In particular, the expressions for the charging, discharging and idle times of the Flyback inductor will be calculated. The main waveforms of the circuit are depicted in Figure 5 and 6, considering the electrical variable references used in the circuit of Figure 4a for each operation mode.
Rectifier Operation
Figure 5a shows the input, the inductor and the DC bus side currents (ig, iLP, iD, respectively) for the rectifier mode. They are detailed for a switching period, T, in Figure 5b together with the inductor voltage, UL. It is agreed that d1 is the duty ratio of the grid side switches, S1 and S2, (i.e., the bidirectional Flyback converter magnetizing inductor charging time); d2 is the duty ratio of the DC bus side switches, SA and SB (during rectifier mode, it imposes the discharging time of the magnetizing inductor). Finally, d3 is the dead time inherent to DCM converters. On the other hand, in the following equations, L is the magnetizing inductance of the grid side inductor and Ug pk is the peak value of the grid voltage.
According to Figure 5b, the average input current for every switching period can be defined as:
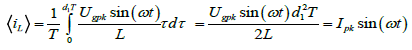 (1)
(1)
From (1), d1 can be written as:
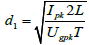 (2)
(2)
The expression of the inductor current in the discharging subinterval can be easily obtained:
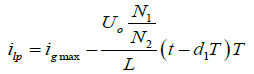 (3)
(3)
Defining d2T as the instant in which the inductor is fully discharged, then:
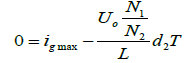 (4)
(4)
Therefore:
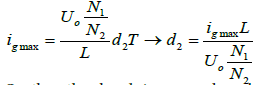 (5)
(5)
On the other hand, iLP max can be calculated for every switching period as follows:
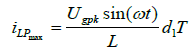 (6)
(6)
Finally, combining (5) and (6):
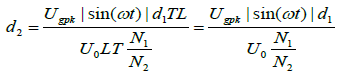 (7)
(7)
After this charge-discharge sequence, the inductor current remains zero for a given interval until the next switching period begins. This last interval is the aforementioned dead time (d3T). As shown in Figure 5b, the operative sequence is d1T for charging, d2T for discharging and d3T as the dead time provided that the converter is operating as a controlled rectifier.
Inverter Operation
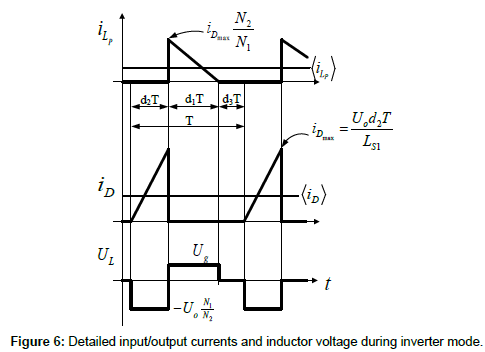
It is critical to notice that the duty ratio intervals sequence will change during inverter mode as shown in Figure 6. Moving now to inverter mode, and in order to be consistent, it is also agreed that d1 is the grid side switches duty ratio, that d2 is the bus side switches duty ratio and that d3 is the dead time. In short, the agreement is the same for both rectifier and inverter modes.
Therefore, during inverter mode, the magnetizing inductor is charged through the switches SA or SB (depending on the grid voltage polarity) for a time interval equal to d2T. Afterwards, the Flyback magnetizing inductor discharges towards the grid side by means of the switches S1 and S2, lasting d1T seconds. Finally, the magnetizing current remains zero during the dead time, d3T, until the next switching period.
References convention for duty ratios and current signs
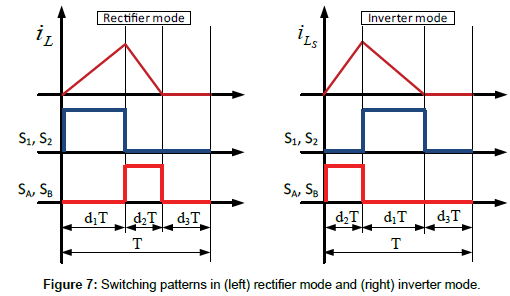
Even though rectifier mode and inverter modes have different sequences, the mathematical expressions to calculate the duty ratios of all the switches are the same in both cases. The switching pattern for both modes in terms of the magnetizing inductors can be seen in Figure 7. This figure defines a problematic situation.
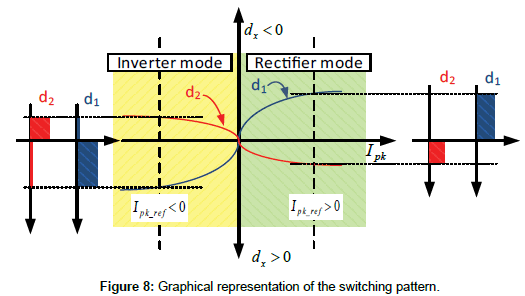
The current reference and the required operating mode of the converter are provided by a droop control strategy (as seen in Figure 3). As a convention, it is assumed that if the current reference Ipk that is used in [2] is greater than zero, then the converter operates in rectifier mode and the Flyback magnetizing inductor is charged through the primary side (grid side). On the other hand, if Ipk is smaller than zero, the magnetizing inductor charges through the DC link at the secondary side, and the converter works in inverter mode. This convention allows defining d1 and d2 independently of the operating mode. Figure 8 summarizes all the possible cases.
Notice how the axes are not conventionally depicted in terms of signs. In inverter mode (yellow area), the current reference of the converter is smaller than zero (Ipk<0) and d1 is considered positive but d2 is assumed to be negative. This definition of a duty ratio might seem surprising. However it is a way to ensure that the charging stage (d2) takes place in advance of the discharging stage (d1). On the contrary, in rectifier mode (green area), the sequence changes: d1 turns out to be negative and d2 positive. Again, the charging stage takes place before the discharging stage; this time d1 accounts for the charging interval. From (2) and (7), the curves d1 and d2 can be represented as in Figure 8. This scheme only defines signs and values for the duty ratios; however another issue needs to be considered for a proper operation of the system: the definition of the firing scheme of the transistors regardless of the operation mode of the converter.
Switching pattern
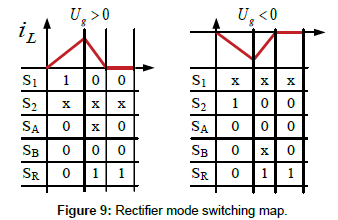
Figs. 9 summarize all the possible on/off states of every switch in the converter for rectifier and inverter modes, respectively. The on state is represented by a logic "1", the off state by a "0", and the undermined state (the switch can be either turned on or off) by an ”x”. In rectifier mode and positive grid voltage (Figure 9 left), the transistor that must drive the grid current is S1 while the diode of S2 would be direct biased (therefore the state of S2 is irrelevant). Similarly, if Ug<0, S2 and the diode of S1 would drive the grid current. Therefore, both transistors can be turned on simultaneously for rectifier mode in the d1 interval (inductor charging). On the other hand, in order to discharge the Flyback transformer, SR must be turned on after S1 is turned off. SA and SB do not affect this discharge due to the fact that their diodes are actually direct biased and driving the current. This analysis simplifies the control of the converter. During d1 interval, S1 and S2 must be turned on, and SA, SB and SR must be turned off, regardless of the input voltage polarity. On the other hand, during d2 and d3 (discharging and dead times), S1, S2, SA and SB can be turned off, while SR must be turned on.
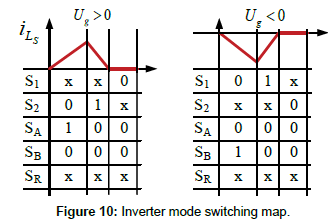
Analogously, the inverter mode switching map is shown in Figure 10. In this case, the magnetizing inductor charges through the bus side and therefore, only SA or SB must be turned on, depending on the polarity of the grid voltage. The diode of SR is direct biased so the state of this switch is irrelevant in this mode. Again, if S1 is turned on, the state of S2 is irrelevant and vice-versa in this operation mode; accordingly both S1 and S2 can be triggered at the same time.
Then, summarizing both tables:
• S1 and S2 can be always turned on and off simultaneously.
• SR can be controlled with the inverted (NOT gate) logic signal used for triggering S1 and S2.
• SA and SB will be turned on/off only in inverter mode, depending on the current reference sign.
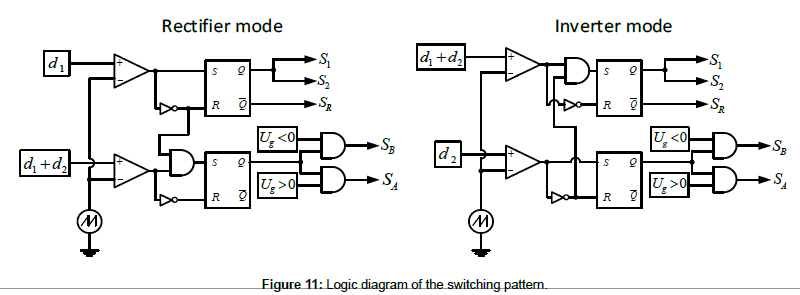
A logic scheme of the firing signals for the switches is shown in Figure 11. It can be seen how the performance of these conditions with logic gates can be a tough task. However, the problem is more efficiently implemented by means of an adequate coding on a digital microcontroller.
Experimental Results and Discussions
Table 1 gathers the main parameters of the laboratory prototype. These parameters have been calculated according to the methodology developed in [13]. Figure 12 shows the prototype built in the laboratory. Notice that detailed waveforms of both rectifier and inverter modes but operating independently can be found in [31].
| Parameter | Symbol | Value |
|---|---|---|
| Converter nominal power input | 100 W | |
| Input Voltage | Ug | 230 Vrms |
| DC link nominal Voltage | Uo | 100 V |
| Switching Frequency | fsw | 50 kHz |
| Grid Side Winding | L | 500 µH |
| Load Side Windings | LS1 , LS2 | 125 µF |
| DC Bus Capacitor | Co | 75 µF |
| Primary Switches | S1 , S2 | FQA8N100C |
| Secondary Switches | SA , SB , SR | IRF740A |
| DSP | TMS320F28335 |
Table 1: Prototype Component.
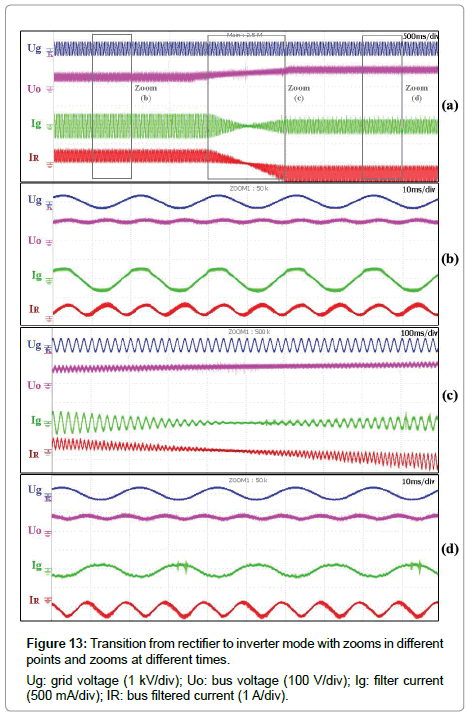
However, in order to validate the key aspect of the control strategy, i.e., the swift transition between modes, several experimental tests have been carried out with the prototype. Figure 13a depicts the behavior of the system when the power converter is demanding +0.25A to supply the lamp. Initially, the Flyback converter is working in rectifier mode (available zoom in Figure 13b). Eventually, it changes to inverter mode gradually, once some extra power is available in the DC bus provided by the RES (zoom in Figure 13c). The usage of film capacitors in the current work causes high fluctuations in the DC link. Including electrolytic ones would dramatically reduce this ripple as well as the converter’s useful life.
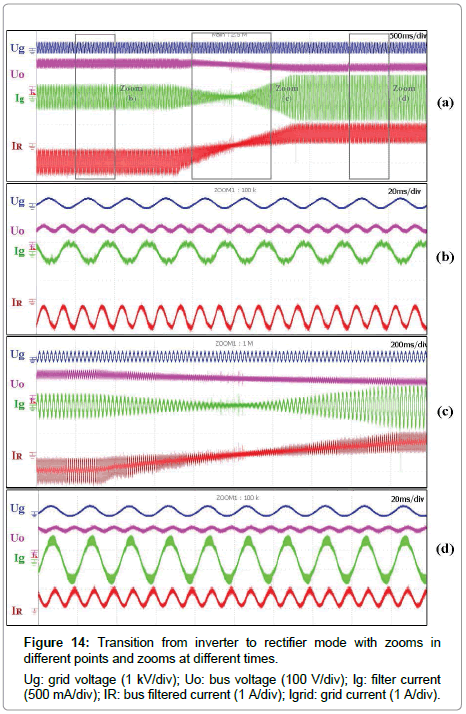
Notice how the current Ig, which represents the grid current (as shown in Figure 4) is in phase with the grid voltage at the beginning since the converter is in rectifier mode. The PF in the current state is 99.6%. When it changes to inverter mode, the same current phaseshifts 180º the grid voltage (zoom in Figure 13d). On the contrary, the second possible case is depicted in Figure 14. This time, the bidirectional Flyback converter initially operates in inverter mode. At a given moment the RES stops injecting power into the DC bus. Therefore, in order to keep the lamp supplied properly, the control responds draining power from the grid.
Conclusions and Future Developments
This work has defined and illustrated the implementation of a unified switching pattern for a bidirectional DCM Flyback converter operating as an active grid interface of a street lighting system with power generation capability. It has been assessed how it is possible to swiftly change from rectifier to inverter mode and vice-versa with the same switching pattern scheme, keeping DCM mode at every instant, therefore allowing for an easy implementation of the stage control at the PWM modules of existing digital microcontrollers. Unlike in previous works [12,13], this control strategy supports the use of storage systems along with RES that can operate all day long, not only during daylight like a PV panel. A mathematical analysis of the equations of the converter has been carried out, as to define the firing state and the duty ratios for every switch in all conditions. A set of simulations has been performed in order to initially validate the idea. Finally, an experimental setup has been built and tested in order to prove the proposed control scheme. The results show how the switching pattern implemented successfully provides the control pulses for every switch in every operation mode, including smooth transitions between them. One possible future development is to explore the feasibility of providing reactive injection capability in the system. The idea is to grant a phase-shift between the converter current and the grid voltage, making interesting to inject or absorb certain amount of reactive power. However, it is a fact that there will be conflicts during the grid voltage zero crossing points.
Acknowledgment
This work has been supported by the Ministry of Economy and Competitiveness of the Government of Spain (MINECO), the Government of the Principality of Asturias and the European Union trough the European Regional Development Fund (ERFD), under Research Grants ENE2013-41491-R (LITCITY Project) and GRUPIN14-076.
References
- Climate Tech Book: Residential and Commercial Sectors Overview.
- Farhangi H (2010) The path of the smart grid. IEEE Power and Energy Magazine 1: 18-28.
- International energy outlook. U.S. Energy Information Administration (EIA), Tech. Rep
- McGarvey T, Morsch A (2016) Local climate action: cities tackle emissions of commercial buildings. Center for climate and energy solutions, U.S. Policy.
- Kjaer S, Pedersen J, Blaabjerg F (2005) A review of single-phase grid connected inverters for photovoltaic modules. IEEE Trans 5: 1292-1306.
- Quintana P, Garcia J, Corominas E, Calleja A, Garcia P (2013) Minimization of current harmonics content in conventional lighting distribution lines without current sensing. IECON 39th Annual Conference of the IEEE.
- Teodorescu R, Liserre M, Rodriguez P (2011) Grid Converters for Photovoltaic and Wind Power Systems.
- Rahmani B, Li W, Liu G (2015) An advanced universal power quality conditioning system and MPPT method for grid integration of photovoltaic systems. INT J ELEC 69: 76-84.
- Dakhel N, Bohgard O (2014) Grid capacity issues with distributed generation A german case study.
- Demirok E (2012) Control of grid interactive pv inverters for high penetration in low voltage distribution networks.
- Rafi F, Hossain M, Lu J (2016) Hierarchical controls selection based on PV penetrations for voltage rise mitigation in a LV distribution network. INT J ELEC 81: 123-139.
- Kroposki B, Lasseter R, Ise T, Morozumi S, Papathanassiou S, et al. (2008) Making microgrids work. Power Energy Mag. 6: 40-53.
- Flores de Melo M, Dotto Vizzotto W, Quintana P, Kirsten A, Dalla Costa M, Garcia J (2015) Bidirectional grid-tie flyback converter applied to distributed power generation and street lighting integrated system. IEEE Transactions 51: 4709-4717.
- Garcia J, Dalla-Costa M, Kirsten A, Gacio D, Quintana P (2012) Study Of A Flyback-Based Stage As Grid Interface Topology for Micro-Generation Applications. 15th International Power Electronics and Motion Control Conference.
- Shimizu T, Wada K, Nakamura N (2006) Flyback-type single-phase utility interactive inverter with power pulsation decoupling on the dc input for an AC photovoltaic module system. IEEE Trans 21: 1264-1272.
- Edwin F, Xiao W, Khadkikar V (2012) Topology review of single phase grid-connected module integrated converters for PV applications. IECON 38th Annual Conference on IEEE Industrial Electronics Society.
- Won DJ, Noh YS, Ryu MY, Won CY, woo Lim H (2014) A study of grid-connected pv-ac module with active power decoupling and ess. IEEE International Conference on Industrial Technology.
- Pragallapati N, Agarwal V (2014 ) Single phase solar pv module integrated flyback based micro-inverter with novel active power decoupling. 7th IET International Conference on Power Electronics, Machines and Drives.
- Hu H, Harb S, Kutkut N, Shen Z, Batarseh I (2013) A single-stage microinverter without using electrolytic capacitors. IEEE Trans 28: 2677-2687.
- GC Christidis, AC Nanakos, and EC Tatakis (2016) Hybrid discontinuous/boundary conduction mode of flyback microinverter for ac-pv modules. IEEE Trans 31: 4195-4205.
- Cho YW, Cha WJ, Kwon JM, Kwon BH (2016) High-efficiency bidirectional dab inverter using a novel hybrid modulation for standalone power generating system with low input voltage. IEEE Trans 31: 4138-4147.
- Everts J, Krismer F, den Keybus JV, Driesen J, Kolar JW (2014) Optimal ZVS Modulation of Single-Phase Single-Stage Bidirectional dab AC DC Converters. IEEE Trans 29: 3954-3970.
- Switch Mode Power Supply Topologies Compared, Wurth Elektronik.
- Pesonen Juha (2014) Improving the Performance of Traditional Flyback-Topology With Two Switch Approach.
- NCP1651-Single Stage Power Factor Controller.
- Tamyurek B, Kirimer B (2015) An interleaved high-power flyback inverter for photovoltaic applications. IEEE Trans 30: 3228-3241.
- Kyritsis A, Tatakis E, Papanikolaou N (2008) Optimum Design of The Current-Source Flyback Inverter for Decentralized Grid-Connected Photovoltaic Systems. IEEE Trans Energy Convers 23: 281-293.
- Tan G, Wang J, Ji Y (2007) Soft-Switching Flyback Inverter With Enhanced Power Decoupling for Photovoltaic Applications. Electr Power App 1: 264-274.
- Chuang SJ, Hong CM , Chen CH (2016) Design of Intelligent Control for Stabilization of Microgrid System. Int J Elec Power 82: 569-578.
- Serban, Ion CP (2017) Microgrid Control Based On A Grid-Forming Inverter Operating As Virtual Synchronous Generator With Enhanced Dynamic Response Capability. Int J Elec Power 89: 94-105.
- Quintana PJ, Garcia J, Cardesin J, Corominas EL (2015) A Unified Switching Strategy In Bidirectional Grid Interface Dcm Flyback Stages For Public Street Lighting Systems With Microgeneration Capability. IEEE Industry Applications Society Annual Meeting.
- Quintana P, Garcia J, Guerrero J, Dragicevic T, Vasquez J (2013) Control Of Single-Phase Islanded Pv/Battery Streetlight Cluster Based On Power-Line Signaling. International Conference on New Concepts in Smart Cities: Fostering Public and Private Alliances.
- Quintana PJ, Guerrero JM, Dragicevic T, Vasquez JC (2014) Control Of Single-Phase Islanded PV/Battery Minigrids Based On Power-Line Signaling. IEEE 11th International Multi-Conference on Systems, Signals & Devices.
- Quintana PJ (2015) Power Electronic Supplies for Public Lighting Systems with Distributed Generation Capability:Solution Proposals for Power and Control Stages, Characterization And Minimization of The Impact In Grid Quality.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi