Research Article, Res J Econ Vol: 1 Issue: 2
Asymmetric Price Adjustment in the London Housing Market: A Disaggregated Analysis
Steven Cook1* and Duncan Watson2
1Department of Accounting and Finance, Swansea University, UK
2School of Economics, University of East Anglia, UK
*Corresponding Author : Steven Cook
Department of Accounting and Finance, Bay Campus, Swansea University, SA1 8EN, UK
Tel: +44(0)1792 602106
E-mail: s.cook@swansea.ac.uk
Received: October 18, 2017 Accepted: November 30, 2017 Published: December 06, 2017
Citation: Cook S, Watson D (2017) Asymmetric Price Adjustment in the London Housing Market: A Disaggregated Analysis. Res J Econ 1:2.
Abstract
The literature on the econometric analysis of UK housing prices is extended via a disaggregated analysis of asymmetric price adjustment in the London market. Using a robust non-parametric approach, extensive asymmetric behaviour is detected. Examination of ‘all properties’ indices reveals a higher level of asymmetric price adjustment in the higher priced Inner London regions relative to Outer London. However, interesting variations in asymmetric behaviour are detected in more detailed analyses involving consideration of alternative classifications of housing. The implications of the dependence of the results on spatial factors and alternative house types are considered.
Keywords: Asymmetry; House prices; Triples test; Dis aggregated data
Introduction
The housing market occupies a central position in the macroeconomy via both its contribution as a major component of personal sector wealth [1] and its linkages with economic fundamentals [2-5]. This importance is reflected by the large empirical literature which has evolved examining the properties of house prices. While the examination of house prices at national and regional levels has a long history with early studies including Nellis et al. [6], Hendry et al. [7], Guissani et al. [8], MacDonald et al. [9] and Alexander et al. [10], a more recent development in the examination of the UK housing market concerns research at a more disaggregated level with price adjustment within the London housing market analysed. Prominent studies in this area are the works of Hamnett et al. [11] and Abbott et al. [12] in which disaggregated (borough-level) data for London are employed to examine dynamic adjustment within this market.
It is the above analyses of Hamnett et al. [11] and Abbott et al. [12] that provide the motivation for the present study. However, in contrast to the focus on the convergence in earlier research, the present study considers the possible presence of asymmetric adjustment in disaggregated London house price data. This analysis extends the existing literature by adding to previous research at a more aggregated level examining asymmetric adjustment in regional UK house prices [13-15]. In addition to examining potential asymmetry in disaggregated London house prices data using the non-parametric Triples test of Randles et al. [16], the current analysis offers a further development by examining asymmetry using data disaggregated further according to house type. Consequently, the present study explores the possibility that asymmetry may vary not only geographically across the boroughs of London, but also across differing types of housing. Importantly, the results obtained provide evidence of an underlying complexity in the evolution of prices in the London housing market which would remain undiscovered without consideration of data disaggregated both geographically and by housing classification.
This paper proceeds as follows. Section (2) provides a selective review of previous research on both the analysis of asymmetric adjustment in macroeconomic time series and the dynamic adjustment of house prices. Importantly, the discussion of house price adjustment considers research at a regional level across the UK and within the London submarket. The data and empirical methods employed in the present analysis are presented in Section (3). Section (4) contains the results of the empirical analysis with some concluding remarks provided in Section (5).
Reviewing previous research
The focus of the current analysis is the examination of potential asymmetric adjustment in house prices within the London housing market using a robust univariate procedure. Consequently, this section provides a short and selective summary of relevant research into (i) the univariate testing for asymmetric adjustment in macroeconomic series and (ii) the empirical analysis of regional house price dynamics within the UK, including the more recent analysis of the London housing market.
An important development in the analysis of asymmetric adjustment in economic series is provided by Sichel et al. [17]. In this seminal study, univariate tests of deepness and steepness were developed to examine the possibility of asymmetry in the both the levels and speeds of adjustment of time series. While deepness considers the possibility that business cycle peaks and troughs may differ in terms of their respective distances from an underlying trend, steepness considers asymmetry in the speeds of adjustment towards these peaks and troughs. This more recent research concerning the quantification of asymmetric adjustment reflects a long history of interest in business cycle asymmetry stretching back to the work of Keynes et al. [18] and the National Bureau of Economic Research [19]. This consideration of asymmetries is illustrated, for example, by Keynes et al. [18] discussion of differing speeds of transition between upward and downward ‘tendencies’ over the course of the business cycle.
The use of Sichel’s tests was promoted within the economics literature by Holly et al. [20] in an analysis of potential asymmetry in UK consumers’ expenditure. This research prompted subsequent studies such as Speight et al. [21] and Cook et al. [22] which provided further applications of Sichel’s tests. While the former study considered asymmetric adjustment across a range of UK macroeconomic variables, the latter study provided a more detailed examination of a durability-asymmetry relationship in consumers’ expenditure motivated by the theoretical analysis of Caballero et al. [23]. However, more recent research involving the univariate analysis of asymmetry has involved the application of the alternative, robust method of Randles et al. [16]. This nonparametric ‘Triples’ test has particular appeal as while a number of alternative tests of asymmetry are available [24], the findings of Randles et al. [16] show the test to have good size and power properties even in small samples while the results of Eubank et al. [25] illustrate its robustness to outliers. As a result of its properties, this test was used to examine asymmetries in UK regional houses by Cook et al. [15]. The results presented in this study for alternative vintages of housing show widespread evidence of significant positive deepness in the following regions: Yorkshire and Humberside, North West, East Midlands, West Midlands, East Anglia, Outer South East, Outer Metropolitan, London and South West. This evidence of positive deepness, or highness, represents cyclical peaks being higher than cyclical troughs are low. In contrast, there is little or no evidence of deepness for the remaining regions of Wales, Scotland and Northern Ireland. In contrast to the findings for deepness limited significant ‘steepness’ is observed except for the East Midlands and Outer South East where a tendency for peaks to be approached more quickly than troughs is apparent.
These univariate findings of Cook et al. [15] concerning asymmetry in regional house prices reflect a growing development in the analysis of regional house prices in the UK. For many years investigators have explored the notion of a ripple effect operating within the UK housing market whereby prices changes are observed firstly in London before spreading to other regions. A variety of techniques such causality analysis, unit root testing, cointegration analysis, principal component analysis, Kalman filtering and autoregressive distributed lag modelling have been employed to examine this hypothesis in studies such as Holmans et al. [26], Guissani et al. [8], MacDonald et al. [9], Alexander et al. [10], Drake et al. [27], Ashworth et al. [28], Meen et al. [29], Petersen et al. [30], Cook et al. [31], Holmes et al. [32], Holmes et al. [33] and Hudson et al. [34]. However, an additional body of research of particular relevance for the current analysis considers the possibility of an asymmetry in the ripple effect with prices converging at differing speeds depending upon whether an underlying equilibrium between regional prices is, or is not, exceeded. This research is illustrated by Cook [13,31] where the momentum threshold autoregressive (MTAR) methods of Tong et al. [35], Enders et al. [36] and Enders et al. [37] are employed to reveal a clear asymmetry in house price convergence.
In addition to exploring potential asymmetric adjustment, recent research in the housing literature has considered a higher level of disaggregation via the analysis of the London housing market. This is an unsurprising development given the value of this market and its position at the centre of the ripple effect. The prominent studies in this area are Hamnett et al. [11] and Abbott et al. [12] where discursive and formal analyses, respectively, are performed to consider potential convergence in house prices in across the different ‘boroughs’ of London. The present study extends these studies of the London market by considering potential asymmetries in the evolution of house prices disaggregated both geographically and by housing type using the univariate Triples test. It should be noted that while Hamnett et al. [11] considers the 32 boroughs of London, Abbott et al. [12] consider the 32 boroughs plus the City of London. While the City of London, or Square Mile, is located in the center of Inner London, it is a local authority but not a borough.
Data and Empirical Methods
The data examined in this paper are quarterly observations over the period 1995 Q1 to 2016 Q4 on mean house prices in the 32 boroughs of London plus the City of London. As noted above, while the City of London is not a borough, it is located in the centre of Inner London and was included in the analysis of Abbott et al. [12]. For these reasons, and to ensure the completeness of the analysis undertaken, the City of London is included in the current examination of the London market. For simplicity, the ‘regions’ of London considered herein are referred to as boroughs despite the inclusion of the (non-borough) City of London. Initially, aggregated or ‘all properties’ indices are considered for each of the boroughs. The analysis then proceeds to consider data disaggregated by type of housing with the four disaggregated classifications being detached, semi-detached and terraced properties and flats. This examination of disaggregated series allows exploration of potential asymmetry within different types of housing which might remain masked by consideration of the aggregate series only. The City of London is included the ‘all properties’ and ‘flats’ indices but not the ‘detached’, ‘semi-detached’ or ‘terraced’ properties indices due to very low numbers of recorded sales in these latter categories. In addition, a (very) limited number of missing values were present in the detached house price series for Hackney, Hammersmith and Fulham, Islington, Newham and Tower Hamlets. These missing values were interpolated using a multiplication cubic spline approach. Further details are available from the authors upon request.
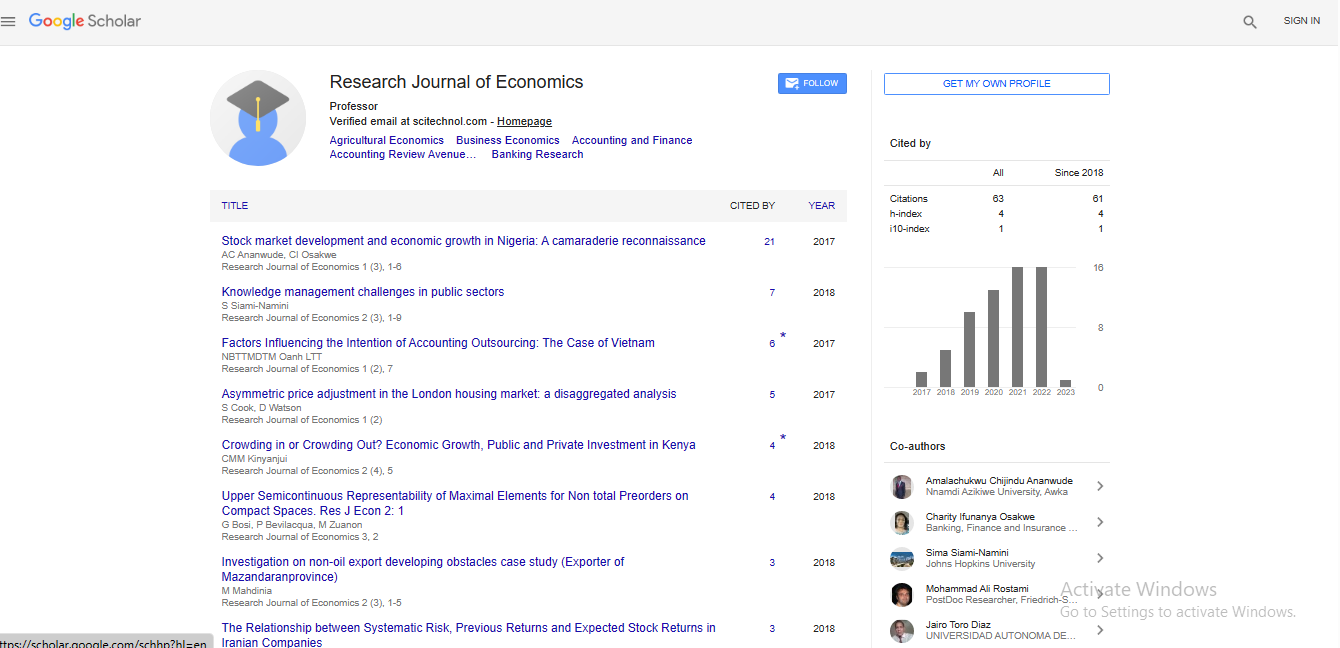
To explore potential cyclical asymmetry, the house price series require detrending, or filtering, ahead of applying the Triples test. Following a standard approach in the literature, this is undertaken using the Hodrick-Prescott et al. [38] (HP) filter. The HP filter is an obvious choice in the present context as it has a linear structure which will not induce spurious asymmetry following its application. Denoting the natural logarithmic values of the house price series as zt, the HP trend (τt) is selected as that minimising the following expression:
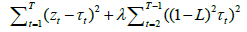 (1)
(1)
Where L is the lag operator such that 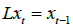 . Clearly (1) is a two-part expression involving both the ‘fit’ and ‘smoothness’ of the trend with the relative weight attached to these determined by the value of the smoothing parameter λ. Given the quarterly frequency of the data considered herein, the conventionally accepted value λ = 1600 is adopted. Following derivation of τt , the required cyclical components (ct) are simply calculated as the difference between each series and its underlying trend as given in (2). The value of 1600 is uncontroversial when analyzing quarterly data and supported by the analysis of Ravn et al. [39].
. Clearly (1) is a two-part expression involving both the ‘fit’ and ‘smoothness’ of the trend with the relative weight attached to these determined by the value of the smoothing parameter λ. Given the quarterly frequency of the data considered herein, the conventionally accepted value λ = 1600 is adopted. Following derivation of τt , the required cyclical components (ct) are simply calculated as the difference between each series and its underlying trend as given in (2). The value of 1600 is uncontroversial when analyzing quarterly data and supported by the analysis of Ravn et al. [39].
 (2)
(2)
With ct calculated for each house price series in turn, the Triples test can be employed to examine potential asymmetry. The means of application of the Triples test can be outlined as follows. The following presentation draws heavily upon Randles et al. [16] where a more complete discussion of the test can be obtained. Given a sample of T observations on ct, the Triples test is based upon recognition that the sample will contain 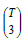 combinations, or sets, of three observations or ‘triples’. Consideration of potential asymmetry is then based upon the distance between the middle value in each triple and each of the two other values. Therefore, for a triple denoted as (ci, cj, ck) where 1≤i≠j≠k≤T, skewness to the right (left) occurs if the middle observation is closer to the smallest (largest) value than the largest (smallest). This can be formalised via consideration of the function f*(ci, cj, ck) given as:
combinations, or sets, of three observations or ‘triples’. Consideration of potential asymmetry is then based upon the distance between the middle value in each triple and each of the two other values. Therefore, for a triple denoted as (ci, cj, ck) where 1≤i≠j≠k≤T, skewness to the right (left) occurs if the middle observation is closer to the smallest (largest) value than the largest (smallest). This can be formalised via consideration of the function f*(ci, cj, ck) given as:
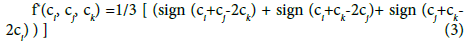
Where sign (a)={-1,0,1} as {a<0, a=0, a >0}. The triple (ci, cj, ck) is a ‘right triple’ if f*(ci, cj, ck) =1/3, while a ‘left triple’ is given by f*(ci, cj, ck) = -1/3, and an absence of skewness in a triple results from f*(ci, cj, ck) =0. Using this expression, Randles et al. [16] propose an estimate of skewness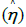 given as:
given as:
 (4)
(4)
The null of symmetry (H0: η=0), is then examined using the test statistic U:
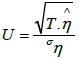 (5)
(5)
Where:
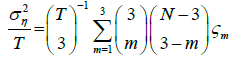 (6)
(6)
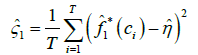 (7)
(7)
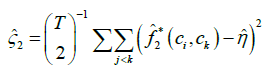 (8)
(8)
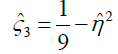 (9)
(9)
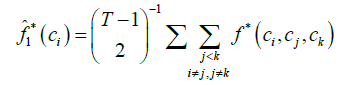 (10)
(10)
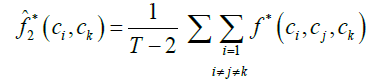 (11)
(11)
The results of Randles et al. [16] show the test statistic U to follow the standard Normal distribution (asymptotically). With the test applied to the cyclical terms, potential deepness can be considered in the form of an asymmetry between the sizes of cyclical peaks and troughs. Via application of the Triples test to the first difference of the cyclical terms 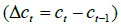 , potential steepness can be considered whereby asymmetry occurs in the form of differing speeds of adjustment towards peaks and troughs. For both deepness and steepness, the sign of the calculated value
, potential steepness can be considered whereby asymmetry occurs in the form of differing speeds of adjustment towards peaks and troughs. For both deepness and steepness, the sign of the calculated value 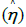 can be used to assess form of any observed significant asymmetry to determine whether there is a difference in the distance of peaks and troughs from trend and whether there is a difference in the speed at which peaks and troughs are approached.
can be used to assess form of any observed significant asymmetry to determine whether there is a difference in the distance of peaks and troughs from trend and whether there is a difference in the speed at which peaks and troughs are approached.
Results
The results obtained from application of the Triples test to the five different house price indices for all boroughs are provided in Tables One to Five. In each instance, the p-value for the test of null of symmetry is reported along with the calculated value of 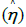 . In combination, these values permit inferences on the presence of significant asymmetry and its form. The discussion below provides an overview of the extent of asymmetric adjustment detected in the London housing market. Following the results of Psaradakis et al. [40], where it was shown that tests of asymmetry may experience reductions in power when applied to series subject to prior filtering, both the 5% and 10% levels are considered to determine significance.
. In combination, these values permit inferences on the presence of significant asymmetry and its form. The discussion below provides an overview of the extent of asymmetric adjustment detected in the London housing market. Following the results of Psaradakis et al. [40], where it was shown that tests of asymmetry may experience reductions in power when applied to series subject to prior filtering, both the 5% and 10% levels are considered to determine significance.
Considering the results for the all properties series, it is apparent that asymmetric behaviour is more apparent in the higher priced Inner London boroughs than the Outer London area. While 71% (86%) of Inner London boroughs display asymmetry in the form of either deepness or steepness (or both in the case of Islington) at 5% (10%) level of significance, the corresponding values are 32% (42%) for Outer London. Within these results it is clear that deepness is more prevalent than steepness. Considering the values of 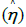 for the significant cases detected, the values for deepness are positive in all but one instance and the negative for steepness in all instances. Hence the overall finding is that higher peaks and prolonged periods of price increases are present in the London market with sharper recessionary, or downturn, periods. In addition, this is more marked for Inner, rather than Outer, London. The results for Islington are of particular interest as the finding of both forms of asymmetry for this borough only reflects its often-discussed unique position in having experienced ‘super-gentrification’.
for the significant cases detected, the values for deepness are positive in all but one instance and the negative for steepness in all instances. Hence the overall finding is that higher peaks and prolonged periods of price increases are present in the London market with sharper recessionary, or downturn, periods. In addition, this is more marked for Inner, rather than Outer, London. The results for Islington are of particular interest as the finding of both forms of asymmetry for this borough only reflects its often-discussed unique position in having experienced ‘super-gentrification’.
Considering the results for alternative classifications of housing presented in Tables Two to five, it is clear that varying degrees of asymmetry are present across these disaggregated series. With regard to the findings for flats in Table Two, Inner London produces similar results to those for ‘all properties’ with identical percentages (71% and 86%) of boroughs with significant results at the 5% and 10% levels. In contrast, the percentage of boroughs in Outer London producing significant results increases relative to the all properties results to 63% (74%) at the 5% (10%) levels of significance when considering flats, with increased levels of both positive deepness and negative steepness noted. Table Three shows the findings for terraced properties to again be similar in nature to those for previous classifications with the percentage of boroughs producing significant results are the 5% (10%) levels being 77% (77%) for Inner London and 47% (74%) for Outer London. However, when the analysis moves to consider semi-detached and detached properties in Tables Four and Five, the findings change. The percentages of boroughs with significant results for Inner London are 38% (54%) for semi-detached properties and 46% (46%) for detached properties. The analogous values for Outer London are 42% (58%) and 32% (47%). A number of specific features are apparent within these results for semi-detached and detached housing in addition to the general finding of an overall decrease in the prevalence of significant asymmetry. One specific feature is the presence of negative significant deepness for both types of housing but particularly for detached properties. This indicates asymmetry in the form of cyclical troughs being further than peaks from the underlying trend. However, the absence of any evidence of significant steepness for detached properties is the most apparent feature of these results. This illustrates an absence of any differing speed of adjustment towards peaks and troughs over the course of the business cycle for this type of housing (Tables 1-5).
| Region | Deepness | Steepness | ||
|---|---|---|---|---|
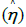 |
p-value | 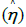 |
p-value | |
| Inner London | ||||
| Camden | 0.036 | 0.034 | -0.028 | 0.089 |
| City of London | 0.014 | 0.248 | 0.005 | 0.404 |
| Hackney | 0.000 | 0.497 | -0.037 | 0.056 |
| Hammersmith and Fulham | 0.027 | 0.063 | -0.005 | 0.397 |
| Haringey | 0.005 | 0.395 | -0.028 | 0.049 |
| Islington | 0.053 | 0.004 | -0.036 | 0.028 |
| Kensington and Chelsea | 0.033 | 0.011 | 0.009 | 0.323 |
| Lambeth | 0.066 | 0.000 | 0.014 | 0.243 |
| Lewisham | 0.021 | 0.143 | -0.039 | 0.015 |
| Newham | 0.037 | 0.002 | -0.006 | 0.398 |
| Southwark | 0.059 | 0.001 | -0.009 | 0.309 |
| Tower Hamlets | 0.024 | 0.080 | 0.020 | 0.151 |
| Wandsworth | 0.051 | 0.000 | -0.002 | 0.447 |
| Westminster | 0.014 | 0.224 | -0.030 | 0.046 |
| Outer London | ||||
| Barking and Dagenham | 0.041 | 0.001 | 0.005 | 0.399 |
| Barnet | 0.000 | 0.492 | -0.006 | 0.387 |
| Bexley | 0.025 | 0.046 | -0.010 | 0.303 |
| Brent | 0.009 | 0.297 | -0.001 | 0.488 |
| Bromley | -0.011 | 0.294 | 0.024 | 0.109 |
| Croydon | 0.028 | 0.058 | -0.015 | 0.254 |
| Ealing | 0.064 | 0.000 | -0.010 | 0.320 |
| Enfield | 0.020 | 0.101 | -0.032 | 0.024 |
| Greenwich | -0.042 | 0.003 | -0.002 | 0.466 |
| Harrow | -0.025 | 0.097 | -0.007 | 0.340 |
| Havering | 0.020 | 0.169 | -0.004 | 0.427 |
| Hillingdon | -0.011 | 0.263 | -0.014 | 0.236 |
| Hounslow | 0.000 | 0.490 | -0.039 | 0.019 |
| Kingston upon Thames | 0.001 | 0.487 | 0.015 | 0.259 |
| Merton | -0.006 | 0.390 | -0.006 | 0.364 |
| Redbridge | -0.010 | 0.301 | -0.011 | 0.308 |
| Richmond upon Thames | 0.046 | 0.003 | 0.007 | 0.360 |
| Sutton | 0.017 | 0.193 | -0.013 | 0.285 |
| Waltham Forest | 0.045 | 0.005 | -0.019 | 0.178 |
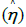 along with p-values for the test of symmetry. To ease interpretation, significance at the 5% level is indicated by the use of shading.
along with p-values for the test of symmetry. To ease interpretation, significance at the 5% level is indicated by the use of shading.Table 1: Triples Test results for all properties.
| Region | Deepness | Steepness | ||
|---|---|---|---|---|
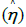 |
p-value | 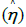 |
p-value | |
| Inner London | ||||
| Camden | 0.029 | 0.067 | -0.041 | 0.033 |
| City of London | 0.020 | 0.132 | 0.003 | 0.438 |
| Hackney | 0.008 | 0.342 | -0.039 | 0.024 |
| Hammersmith and Fulham | 0.060 | 0.000 | -0.017 | 0.206 |
| Haringey | 0.000 | 0.496 | -0.024 | 0.072 |
| Islington | 0.029 | 0.082 | 0.015 | 0.246 |
| Kensington and Chelsea | 0.014 | 0.205 | 0.007 | 0.381 |
| Lambeth | 0.045 | 0.001 | 0.043 | 0.017 |
| Lewisham | 0.047 | 0.005 | -0.032 | 0.055 |
| Newham | 0.055 | 0.004 | 0.004 | 0.434 |
| Southwark | 0.045 | 0.003 | 0.010 | 0.288 |
| Tower Hamlets | 0.006 | 0.356 | 0.028 | 0.051 |
| Wandsworth | 0.035 | 0.022 | 0.036 | 0.030 |
| Westminster | 0.030 | 0.039 | -0.017 | 0.185 |
| Outer London | ||||
| Barking and Dagenham | 0.018 | 0.133 | -0.018 | 0.118 |
| Barnet | 0.007 | 0.345 | -0.014 | 0.258 |
| Bexley | 0.052 | 0.001 | 0.026 | 0.067 |
| Brent | 0.044 | 0.007 | 0.005 | 0.390 |
| Bromley | 0.033 | 0.072 | -0.024 | 0.066 |
| Croydon | 0.009 | 0.324 | -0.049 | 0.001 |
| Ealing | 0.063 | 0.000 | -0.032 | 0.040 |
| Enfield | 0.047 | 0.001 | 0.002 | 0.446 |
| Greenwich | -0.008 | 0.318 | 0.012 | 0.271 |
| Harrow | -0.018 | 0.125 | -0.014 | 0.227 |
| Havering | 0.044 | 0.003 | -0.029 | 0.047 |
| Hillingdon | 0.047 | 0.006 | -0.001 | 0.484 |
| Hounslow | 0.013 | 0.242 | -0.053 | 0.001 |
| Kingston upon Thames | 0.030 | 0.049 | -0.004 | 0.431 |
| Merton | -0.012 | 0.259 | -0.042 | 0.007 |
| Redbridge | 0.008 | 0.284 | 0.003 | 0.445 |
| Richmond upon Thames | 0.024 | 0.065 | -0.012 | 0.271 |
| Sutton | 0.046 | 0.008 | -0.036 | 0.036 |
| Waltham Forest | 0.043 | 0.006 | -0.011 | 0.298 |
Table 2: Triples Test results for flats.
| Region | Deepness | Steepness | ||
|---|---|---|---|---|
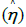 |
p-value | 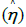 |
p-value | |
| Inner London | ||||
| Camden | 0.010 | 0.323 | -0.014 | 0.251 |
| City of London | N/A | N/A | ||
| Hackney | 0.049 | 0.005 | -0.024 | 0.131 |
| Hammersmith and Fulham | 0.030 | 0.062 | -0.034 | 0.035 |
| Haringey | 0.019 | 0.204 | -0.006 | 0.374 |
| Islington | 0.038 | 0.031 | -0.003 | 0.442 |
| Kensington and Chelsea | 0.054 | 0.001 | 0.027 | 0.077 |
| Lambeth | 0.054 | 0.004 | 0.010 | 0.326 |
| Lewisham | 0.022 | 0.143 | -0.016 | 0.210 |
| Newham | 0.030 | 0.016 | -0.007 | 0.369 |
| Southwark | 0.038 | 0.012 | -0.001 | 0.480 |
| Tower Hamlets | 0.035 | 0.032 | -0.022 | 0.149 |
| Wandsworth | 0.064 | 0.000 | 0.001 | 0.474 |
| Westminster | 0.053 | 0.000 | 0.002 | 0.454 |
| Outer London | ||||
| Barking and Dagenham | 0.051 | 0.000 | 0.007 | 0.369 |
| Barnet | 0.008 | 0.326 | -0.038 | 0.018 |
| Bexley | 0.031 | 0.022 | -0.001 | 0.470 |
| Brent | -0.006 | 0.388 | 0.023 | 0.093 |
| Bromley | 0.003 | 0.441 | -0.024 | 0.119 |
| Croydon | 0.043 | 0.014 | -0.041 | 0.036 |
| Ealing | 0.022 | 0.093 | -0.028 | 0.066 |
| Enfield | 0.038 | 0.011 | -0.026 | 0.073 |
| Greenwich | -0.018 | 0.143 | 0.008 | 0.316 |
| Harrow | 0.030 | 0.034 | -0.018 | 0.192 |
| Havering | 0.050 | 0.000 | 0.008 | 0.362 |
| Hillingdon | -0.011 | 0.265 | -0.019 | 0.157 |
| Hounslow | 0.026 | 0.087 | 0.005 | 0.399 |
| Kingston upon Thames | 0.006 | 0.391 | -0.026 | 0.100 |
| Merton | -0.001 | 0.485 | -0.001 | 0.485 |
| Redbridge | 0.023 | 0.088 | -0.030 | 0.066 |
| Richmond upon Thames | 0.035 | 0.044 | 0.018 | 0.209 |
| Sutton | 0.016 | 0.212 | -0.034 | 0.046 |
| Waltham Forest | 0.019 | 0.137 | 0.000 | 0.492 |
Table 3: Triples Test results for terraced properties.
| Region | Deepness | Steepness | ||
|---|---|---|---|---|
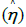 |
p-value | 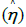 |
p-value | |
| Inner London | ||||
| Camden | 0.019 | 0.159 | -0.016 | 0.202 |
| City of London | N/A | N/A | ||
| Hackney | 0.041 | 0.003 | -0.023 | 0.086 |
| Hammersmith and Fulham | -0.046 | 0.007 | 0.006 | 0.395 |
| Haringey | 0.020 | 0.115 | 0.004 | 0.413 |
| Islington | -0.001 | 0.482 | -0.027 | 0.091 |
| Kensington and Chelsea | 0.019 | 0.136 | -0.015 | 0.270 |
| Lambeth | 0.016 | 0.234 | 0.007 | 0.371 |
| Lewisham | -0.001 | 0.479 | -0.006 | 0.360 |
| Newham | 0.011 | 0.253 | -0.052 | 0.006 |
| Southwark | 0.013 | 0.194 | -0.017 | 0.179 |
| Tower Hamlets | 0.010 | 0.275 | 0.032 | 0.034 |
| Wandsworth | 0.024 | 0.099 | -0.003 | 0.437 |
| Westminster | 0.011 | 0.276 | -0.031 | 0.025 |
| Outer London | ||||
| Barking and Dagenham | 0.049 | 0.001 | -0.017 | 0.205 |
| Barnet | 0.019 | 0.160 | 0.008 | 0.343 |
| Bexley | 0.019 | 0.137 | -0.009 | 0.330 |
| Brent | -0.016 | 0.191 | -0.013 | 0.266 |
| Bromley | -0.002 | 0.466 | -0.021 | 0.142 |
| Croydon | -0.002 | 0.465 | -0.008 | 0.348 |
| Ealing | 0.030 | 0.039 | -0.045 | 0.003 |
| Enfield | 0.037 | 0.017 | -0.018 | 0.205 |
| Greenwich | 0.055 | 0.000 | -0.011 | 0.283 |
| Harrow | 0.014 | 0.245 | -0.009 | 0.317 |
| Havering | 0.046 | 0.001 | -0.026 | 0.080 |
| Hillingdon | 0.025 | 0.064 | -0.006 | 0.393 |
| Hounslow | -0.030 | 0.041 | -0.020 | 0.152 |
| Kingston upon Thames | 0.029 | 0.093 | 0.009 | 0.338 |
| Merton | 0.019 | 0.130 | 0.015 | 0.216 |
| Redbridge | 0.028 | 0.060 | -0.034 | 0.029 |
| Richmond upon Thames | 0.039 | 0.010 | 0.003 | 0.437 |
| Sutton | 0.023 | 0.136 | -0.025 | 0.131 |
| Waltham Forest | 0.026 | 0.080 | 0.016 | 0.231 |
Table 4: Triples Test results for semi-detached properties.
| Region | Deepness | Steepness | ||
|---|---|---|---|---|
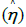 |
p-value | 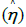 |
p-value | |
| Inner London | ||||
| Camden | -0.010 | 0.256 | 0.004 | 0.411 |
| City of London | N/A | N/A | ||
| Hackney | -0.058 | 0.000 | -0.001 | 0.481 |
| Hammersmith and Fulham | 0.016 | 0.224 | 0.003 | 0.431 |
| Haringey | -0.044 | 0.006 | 0.014 | 0.229 |
| Islington | 0.049 | 0.007 | 0.027 | 0.121 |
| Kensington and Chelsea | -0.024 | 0.118 | 0.008 | 0.366 |
| Lambeth | 0.004 | 0.415 | 0.019 | 0.151 |
| Lewisham | -0.022 | 0.097 | -0.002 | 0.459 |
| Newham | 0.031 | 0.023 | 0.022 | 0.122 |
| Southwark | 0.002 | 0.458 | 0.006 | 0.401 |
| Tower Hamlets | 0.021 | 0.104 | 0.001 | 0.479 |
| Wandsworth | 0.024 | 0.088 | -0.013 | 0.280 |
| Westminster | 0.002 | 0.463 | 0.004 | 0.426 |
| Outer London | ||||
| Barking and Dagenham | -0.026 | 0.099 | 0.011 | 0.311 |
| Barnet | -0.010 | 0.318 | -0.006 | 0.378 |
| Bexley | -0.023 | 0.089 | -0.010 | 0.313 |
| Brent | -0.047 | 0.006 | 0.008 | 0.365 |
| Bromley | 0.023 | 0.095 | 0.019 | 0.177 |
| Croydon | 0.013 | 0.233 | -0.019 | 0.131 |
| Ealing | 0.037 | 0.035 | 0.028 | 0.138 |
| Enfield | 0.021 | 0.144 | 0.006 | 0.392 |
| Greenwich | 0.041 | 0.024 | 0.015 | 0.198 |
| Harrow | -0.023 | 0.103 | -0.010 | 0.297 |
| Havering | -0.005 | 0.385 | 0.004 | 0.434 |
| Hillingdon | -0.061 | 0.000 | -0.001 | 0.470 |
| Hounslow | 0.043 | 0.005 | -0.003 | 0.452 |
| Kingston upon Thames | 0.021 | 0.135 | -0.003 | 0.441 |
| Merton | 0.016 | 0.174 | 0.022 | 0.123 |
| Redbridge | 0.010 | 0.281 | -0.015 | 0.187 |
| Richmond upon Thames | 0.024 | 0.104 | 0.007 | 0.365 |
| Sutton | 0.020 | 0.152 | -0.016 | 0.211 |
| Waltham Forest | 0.045 | 0.012 | -0.027 | 0.137 |
Table 5: Triples Test results for detached properties.
Conclusion
The findings of the present paper extend both the large literature on the analysis of asymmetric adjustment in house prices and the growing body of research into price adjustment across regions within the UK housing market. The application of a robust univariate approach detected widespread evidence of asymmetric adjustment in ‘all properties’ indices for numerous London boroughs, particularly within the higher priced Inner London region. The nature of the asymmetry observed indicated prolonged upswings in the market to pronounced cyclical peaks along with sharper recessionary or contractionary periods. However, further investigation showed the results for all properties to mask interesting variations across alternative classifications of housing. Interestingly, the degree of asymmetric adjustment detected in Inner London prices fell when moving from flats to terraced properties to semi-detached houses. While an increase was observed when moving from semidetached to detached properties, this was a marginal increase. In a similar manner, the results for Outer London showed detection of asymmetry to fall when moving from all properties index through to the detached properties index. However, the reduction in noted asymmetric adjustment when moving between housing types was less pronounced than that for the Inner London area and for the semi-detached properties index, a higher percentage of boroughs exhibiting asymmetry were found for Outer London boroughs than for Inner London boroughs. This is in part due to the prevalence of such properties in these ‘leafy’, ‘pleasant’ or ‘suburban’ boroughs [12].
The message to be taken from the above analysis is that the degree of disaggregation and incorporation of potential asymmetry are both crucial in the modelling or analysis of the London housing market. With regard to disaggregation, both geography and housing classification reveal otherwise hidden variations in house prices. Considering the presence of asymmetry, it is inadvisable for future research to consider simple linear or symmetric approaches given their possible misspecification and generation of spurious results. The varying degrees of asymmetry detected across boroughs and house types warrant further investigation with notions of displaced demand [11], the ability to move between differing types of housing and spillover effects between contiguous boroughs potentially fruitful lines of investigation.
References
- Holly S, Jones N (1997) House prices since the 1940s: Cointegration, demography and asymmetries. Econ Model 14: 549-565.
- Gallin J (2006) The long-run relationship between house prices and income: Evidence from local housing markets. Real Estate Econ 34: 417-438.
- Goodhart C, Hofmann B (2007) House Prices and the Macroeconomy: Implications for Banking and Price Stability, USA.
- Costello G, Fraser P, Groenewold N (2011) House prices, non-fundamental components and interstate spillovers: The Australian experience. J Bank Financ 35: 653-669.
- Han L (2013) Understanding the puzzling risk-return relationship for housing. Rev Financ Studies 26: 877-928.
- Nellis JG, Longbottom JA (1981) An empirical analysis of the determination of house prices in the United Kingdom. Urban Studies 18: 9-22.
- Hendry DF (1984) Econometric modelling of house prices in the United Kingdom, UK.
- Giussani B, Hadjimatheou G (1991) Modelling regional house prices in the United Kingdom. Papers in Regional Science 70: 201-219.
- MacDonald R, Taylor MP (1993) Regional house prices in Britain: Long-run relationships and short-run dynamics. Scot J Polit Econ 40: 43-55.
- Alexander C, Barrow M (1994) Seasonality and cointegration of regional house prices in the UK. Urban Studies 31: 1667-1689.
- Hamnett C (2009) Spatially displaced demand and the changing geography of house prices in London, 1995-2006. Housing Studies 24: 301-320.
- Abbott A, De Vita G (2012) Pairwise convergence of district-level house prices in London. Urban Studies 49: 719-738.
- Cook S (2003) The convergence of regional house prices in the UK. Urban Studies 40: 2285-2294.
- Cook S (2005a) Detecting long-run relationships in regional house prices in the UK. Intern Rev App Econ 19: 107-118.
- Cook S (2006) A non-parametric examination of asymmetrical behaviour in the UK housing market. Urban Studies 47: 2067-2074.
- Randles RH, Fligner MA, Policello GE, Wolfe DA (1980) An asymptotically distribution-free test for symmetry versus asymmetry. J Am Stat Assoc 75: 168-172.
- Sichel D (1993) Business cycle asymmetry: A deeper look. Economic Inquiry 31: 224-236.
- Keynes JM (1936) A General Theory of Employment, Interest and Money. London
- Burns AF, Mitchell WC (1946) Measuring Business Cycles. National Bureau of Economic Research: New York.
- Holly S, Stannett M (1995) Are there asymmetries in UK consumption? A time series analysis. Applied Economics 27: 767-772.
- Speight AE, McMillan DG (1998) Testing for asymmetries in UK macroeconomic time series. Scot J Polit Econ 45: 158-170.
- Cook S (2000) Durability and asymmetry in UK consumers’ expenditure. Intern Rev Applied Econ 14: 111-119.
- Caballero R (1993) Durable goods: An explanation for their slow adjustment. J Political Econ 101: 351-384.
- Psaradakis Z (2000) p-value adjustments for multiple tests for nonlinearity. Stud Nonlinear Dyn E 4: 95-100.
- Eubank RL, LaRiccia VN, Rosenstein RB (1992) Testing symmetry about an unknown median via linear rank procedures. Nonparametric Statistics 1: 301-311.
- Holmans A (1990) House price changes through time at national and sub-national level. Government Economic Service Working Paper 110.
- Drake L (1995) Testing for convergence between UK regional house prices. Regional Studies 29: 357-366.
- Ashworth J, Parker SC (1997) Modelling regional house prices in the UK. Scot J Polit Econ 44: 225-246.
- Meen G (1999) Regional house prices and the ripple effect: A new interpretation. Housing Studies 14: 733-753.
- Peterson W, Holly S, Gaudoin P (2002) Further Work on an Economic Model of the Demand for Social Housing. Report to the Department of the Environment, Transport and Regions.
- Cook S (2005b) Regional house price behaviour in the UK: Application of a joint testing procedure. Physica A 345: 611-621.
- Holmes M (2007) How convergent are regional house prices in the United Kingdom? Some new evidence from panel data unit root testing. J Econ Social Res 9: 1-17.
- Holmes M, Grimes A (2008) Is there long-run convergence among regional house prices in the UK? Urban Studies 45: 1531-1544.
- Hudson C, Hudson J, Morley B (2017) Differing house price linkages across UK regions: A multi-dimensional recursive ripple model. Urban Studies.
- Tong H (1990) Non-linear time-series: A dynamical approach, USA
- Enders W, Granger CW (1998) Unit root tests and asymmetric adjustment with an example using the term structure of interest rates. J Bus Econ Stat 16: 304-311.
- Enders W, Siklos P (2000) Cointegration and threshold adjustment. J Bus Econ Stat 19: 166-176.
- Hodrick R, Prescott E (1997) Post-war US business cycles: An empirical investigation. J Money Credit Banking 29: 1-16.
- Ravn M, Uhlig H (2002) On adjusting the Hodrick-Prescott filter for the frequency of observations. Rev Econ Stat 84: 371-380.
- Psaradakis Z, Sola M (2003) On detrending and cyclical asymmetry. J Appl Econom 18: 271-289.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi