Research Article, J Comput Eng Inf Technol Vol: 6 Issue: 3
Dissimilarity of Graph Invariant Features from EEG Phase-space Analysis
Patrick Luckett1*, J Todd McDonald1 and Lee M Hively2
1School of Computing, University of South Alabama USA
*Corresponding Author : Patrick Luckett
School of Computing, University of South Alabama, USA
Tel: 251-300-0944
E-mail: phl801@jagmail.southalabama.edu
Received: April 20, 2017 Accepted: May 17, 2017 Published: May 23, 2017
Citation: Luckett P, McDonald JT, Hively LM (2017) Dissimilarity of Graph Invariant Features from EEG Phase-space Analysis. J Comput Eng Inf Technol 6:3. doi: 10.4172/2324-9307.1000172
Abstract
Electroencephalogram (EEG) data has been used in a variety of linear and nonlinear time series analysis techniques for predicting epileptic seizures. We examine phase-space dissimilarity measures for forewarning of seizure events based on time-delay embedding and state space recreation of the underlying brain dynamics.
Given novel states which form graph nodes and dynamical linkages between states which form graph edges, we use graph dissimilarity to detect dynamical phase shifts which indicate the onset of epileptic events. In this paper, we report on observed trends and characteristics of graphs based on event and nonevent data from human EEG observations, and extend previous work focused on node and link dissimilarity by analyzing other graph properties as well. Our analysis includes measured properties and dissimilarity features that influence forewarning prediction accuracy.
Keywords: Graph theory; Phase-space dissimilarity; Nonlinear dynamics; EEG analysis; Epilepsy forewarning
Introduction
Epilepsy afflicts about 1% of the world’s population. Seizures are usually not serious medical events, but may become lifethreatening during hazardous activities (e.g., driving or swimming alone). However, extreme epileptic events require immediate medical intervention to avoid sudden unexplained death, which is characterized by fatal cardiac arrhythmia and/or breathing cessation, along with concomitant injuries. Two-thirds of patients have events that are controllable by anti-epileptic drugs, which frequently have debilitating side effects (e.g., tiredness, memory problems, dizziness, mood problems, seizure continuation, difficulty concentrating, headaches, appetite problems, shaking). Another 7-8% can be cured by epilepsy surgery, which may result in cognitive impairments or post-operation infection which could lead to death. For the remaining one-quarter of people with epilepsy, no available therapy is effective. Quality-of-life issues include fear of the next seizure, inability to drive, social issues, work problems, depression, fatigue, school issues, and increased stress [1]. Reliable seizure forewarning would drastically alter seizure treatment, allowing preventive action (e.g., episodic seizure medication rather than continuous anti- seizure drugs). Potential improvements to the patient’s quality of life include: reduced morbidity and mortality risk, fewer hospital re-admissions for seizures, lower medical costs, less work/school absenteeism, and retention of driving privileges.
The purpose of this paper is to extend previous work by Hively et al. [2-8]; Protopopescu et al. [9] and Gailey et al. [10] in forewarning of seizure events using theorem-based phase space analysis methodology by
Identify and analyze graph features and characteristics de- rived from EEG data not previously used as a measure of dissimilarity, and evaluate the performance of these features as dissimilarity measures in phase space analysis.
Identify graph features and properties relative to phase space graphs formed by EEG data. We believe the analysis of previously unstudied graph features and properties in phase space analysis could lead to a higher accuracy rate and improved forewarning prediction distance.
Background
Nonlinear EEG measures are non-stationary, displaying marked transitions between normal and epileptic states [11,12]. EEG also exhibit low-dimensional features [13,14] with at least one positive Lyapunov exponent [14-16], and hence positive Kolmogorov entropy. EEG have clear phase-space structure [14-16], which our analysis uses to extract condition change. However, one would not expect longterm dynamical changes for an abrupt transition to a seizure [17], for example activated by flashing lights, sound, or temperature.
Recent research focuses on statistical tests of forewarning. Such statistical tests are part of a long-standing hard problem of forewarning, such as earthquakes, machine failures, and biomedical events [18]. Recent reviews [19-21] concluded that the work (Figure 1).
to date does not provide convincing statistical evidence for seizure forewarning. Mormann et al. [19] suggest guidelines for methodological soundness of seizure pre- diction studies:
Testing of prediction on unselected continuous long-term (several days) EEG from each patient;
Results with calculation of sensitivity and specificity for a specific prediction horizon;
Testing of false positives via Monte Carlo simulations or nave prediction schemes;
In-sample training of prediction algorithms, followed by out-ofsample tests on independent data.
Winterhalder et al. [22] further suggest that a maximum false positive (FP) rate of 0.015 FP/hour is rea- sonable. Several recent papers address specific statistical tests of epilepsy prediction as different from chance [23,24].
Our analysis focuses on noninvasive scalp EEG readings. Scalp EEG readings are notoriously contaminated by noisy artifacts such as eye blinks and other muscular movements, and have resisted previous analyses due to signal attenuation through bone and soft tis- sue. Our initial analysis [25] demonstrated a zero-phase quadratic filter that removed the artifacts in scalp EEG. That analysis used traditional nonlinear measures, TNM (Kolmogorov entropy, correlation dimension, and mutual information), which yielded inconsistent forewarning. Our subsequent work [2-10] demonstrated phase-space dissimilarity measures (PSDM), which sum the absolute value of differences. By contrast, TNM are based on a difference of averages. PSDM provide consistently better forewarning than TNM, independent of patients’ age, sex, event onset time, pre-event activity, or awake- versus asleep-state baseline state.
Previously, we limited the forewarning analysis to 1 hour before the clinically characterized seizure. This time horizon was motivated by:
Whether any forewarning can be obtained; and
Forewarning of more than 1 hour was generally considered too long/uncertain to be clinically useful.
However, work by Litt and Echauz [26] demonstrated forewarning of several hours before the epileptic events. Consequently, subsequent work Hively et al. [25] extended the time window to the full length of the data, yielding forewarning times of 6 hours, consistent with Litt and Echauz [26]. Our previous work [2-10] also used forewarning indication (or lack thereof in non- event datasets) in any one channel, regardless of the results in other channels. However, the any-one channel criterion is not definitive, because a true positive (negative) in one channel can be accompanied by a false negative (positive) in other channel(s). Thus, our subsequent work [8-10,25] used scalp EEG from two fixed channels with an accuracy of 58/60, sensitivity = 40/40, and specificity = 18/20. However, this result decreases abruptly for a unit change in any of the analysis parameters. Also, these test only used node and link differences to measure dissimilarity among graphs.
EEG Phase Space Reconstruction
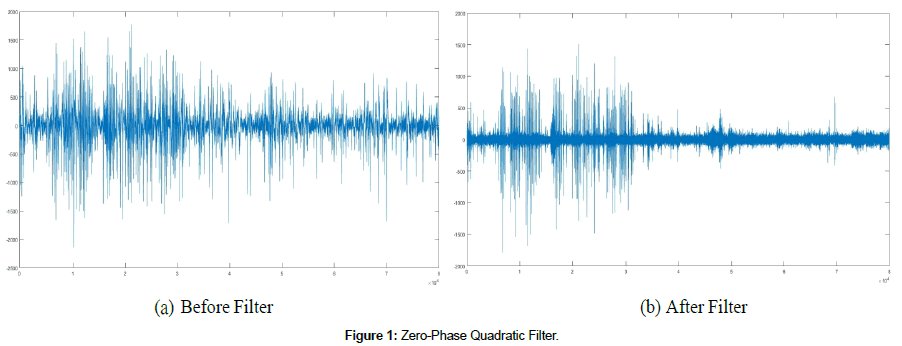
We model the nonlinear dynamics of the brain using time-serial EEG data. Specifically, the analysis uses time-serial EEG data in the 10- 20 system from two scalp electrodes, e.g., F8 and FP2, to form a single channel of data in the bipolar montage. These data were uniformly sampled in time, ti, at 250 Hz, giving N time-serial points in each analysis window (cutset), ei = e(ti). A novel zero- phase, quadratic filter removes electrical activity from eye blinks and other muscular artifacts, which otherwise obscure the event forewarning. This novel filter retains the nonlinear amplitude and phase information [8]. The filter uses a moving window of 2w + 1 points of ei-data, which are fitted to a parabola in a least-squares sense, yielding N-2w points of artifact data, fi. Figure 1 shows a single cutset before the quadriatic filter (ei) and after the filter is applied (gi).
The residual (artifact-filtered) signal has essentially no lowfrequency artifacts, gi = ei - fi. We then represent every gi in a symbolized form si. The number of symbols is a predetermined parameter such that si is one of S different integers 0,1,,,S-1:
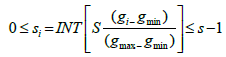 (1)
(1)
Here, INT rounds the calculated value down to the lowest integer, and gmax and gmin represent the largest and smallest values of gi respectively. Takens? theorem [27] gives a smooth, non-intersecting dynamical reconstruction in a sufficiently high dimensional space by a time- delay embedding. Thus, Takens? theorem allows the symbolized data to be converted into phase-space vec- tors yi:
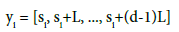 (2)
(2)
Takens’ theorem allows the yi states to capture the topology (connectivity) of the underlying dynamics. This theorem assumes the underlying observable is a real, twice-differentiable function of typical dynamics without special symmetries. The time-delay lag is L, which must not be too small (making si and si+L indistinguishable) or too large (making si and si+L independent by long- time unpredictability). The embedding dimension is d, which must be sufficiently large to capture the dynamics, but not too large to avoid over-fitting. Takens theorem also provides a metric (e.g., Euclidean distance in d dimensions) between the phase-space points. The states from Eq. (2) are nodes. The process flow, yi -> yi+M, forms state-to-state links, for some lag, M. The nodes and links form a ’’graph” with topologicallyinvariant measures that are independent of any unique labeling of nodes and links. By dividing the data into cutsets, and representing each cutsets with as a graph, we can use dissimilarity measures between the graphs among the cutset compared to graphs from base cases (non-event) to predict a seizure event. Table 1 describes the properties of graphs produced in each cutset per parameter set.
| Set ID | Acyclic | Biconnected | Bipartite | Connected | Cyclic | Forrest | MEF | BT | Plannar | RT | LF | Simple | SC | Tree |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | False | False | False | True | True | False | False | False | False | False | True | True | T/F | Falseeee |
| P2 | False | False | False | True | True | False | False | False | False | False | True | True | T/F | False |
| P3 | False | T/F | False | True | True | False | False | False | False | False | True | True | T/F | False |
| P4 | False | T/F | False | True | True | False | False | False | False | False | True | True | T/F | False |
| P5 | False | False | False | True | True | False | False | False | False | False | True | True | True | False |
| P6 | False | False | False | True | True | False | False | False | False | False | True | True | T/F | False |
| P7 | False | False | False | True | True | False | False | False | False | False | True | True | T/F | False |
| P8 | False | False | False | True | True | False | False | False | False | False | True | True | T/F | False |
| P9 | False | T/F | False | True | True | False | False | False | False | False | True | True | True | False |
| P10 | False | False | False | True | True | False | False | False | False | False | True | True | T/F | False |
Table 1: Graph Properties.
Related Work
Epileptic seizure prediction has been studied significantly using a variety of techniques and a variety of psychological data. The first attempt to predict seizures were made by Viglione and colleagues in 1970 [28]. Recent techniques used include frequency-based methods, statistical analysis, non-linear dynamics, and intelligent engineered systems [26]. Wackermann and Allefeld [29] used state space reconstruction to represent dynamics in neural activity from EEG data. Mirowski et al. [30] used bivariate features of EEG synchronization over consecutive time points to form patterns, and then used ma- chine learning-based classifiers, such as SVMs and neural networks, to correctly identify interictal and preictal patterns of features. Stam and Reijneveld [31] note that nonlinear dynamics, statistical physics, and graph theory are useful tool when analyzing complex networks such as the human brain, and discuss their applications to neuroscience through modeling neural dynamics, graph analysis of neuroanatomical networks and graph analysis of functional magnetic resonance imaging, electroencephalography, and magnetoencephalography. Drentrup et al. [32] showed improved prediction performance by combining mean phase coherence and dynamic similarity index to long-term continuous intracranial EEG data, and suggest combining prediction methods is a promising approach to enhance seizure prediction performance. Zijlmans et al. [33] use the presence of high frequency osculations in EEG readings sampled at (Figure 2) a frequency of at least 2,000Hz as a biomarker to identify the presence of epileptogenic tissue. By identi- fying these biomarkers, patients requiring surgery have a better chance of rehabilitation. Relying on patterns in EEG features prior to a seizure, Raghunathan et al. [34] proposed a two stage computationally efficient algorithm that detected seizures within 9% of their duration after onset. Mirowski et al. [35] used convolutional networks and wavelet coherence to successfully predict seizures based on bivariate features of EEG synchronization, including crosscorrelation, nonlinear interdependence, dynamical entrainment and wavelet synchrony. Their method showed pattern recognition could capture seizure pre- cursors through the spatiotemporal dynamics of EEG synchronization. Mirowski [36] also compared L1-regularized logistic regression, convolutional networks, and support vector machines on aggregated features among EEG channels, including cross-correlation, nonlinear interde- pendence, Lyapunov exponents, and wavelet analysis- based synchrony such as phase locking. Yuan et al. [37], state the behavior of embedding dimension reflects the variation of freedom degree of brain nonlinear dynamics during seizures, and based on Cao’s method, nor- mal EEG signals are somewhat random, whereas epileptic EEG signals have determinism. Astolfi et al. [38] used graph theory to interpret connectivity patterns estimated on the cortical surface in different frequency bands after imaging, which suggest their methodology could identify differences in functional connectivity patterns elicited by different tasks and conditions. D’Alessandro et al. [39] suggest a seizure prediction method using feature selection methods over multiple EEG channels. Their approach involves an individual based method for selecting EEG features and electrode channel locations based on precursors that occur within ten minutes of seizure onset using intelligent genetic search algorithms to EEG signals collected from multiple intracranial readings and multiple features derived from these signals. Adeli et al. [40] presented a seizure prediction method based on quantifying the nonlinear dynamics of EEGs using the correlation dimension, which represents complexity, and the largest Lyapunov exponent, which represents chaoticity within the system. Their method isolated changes in correla- tion dimensions and Lyapunov exponents in specific subbands of EEG readings. Firpi et al. [41] used artificial features, created using genetic programming modules and a k-nearest neighbor classifier, to create synthetic features formed from reconstructed state-space trajectories of intracranial EEG signals to reveal patterns indicative of epileptic seizure onset. In a 2014 paper published by the National Institute of Health, Chiang et al. [42] stated graph theory allows for a network-based representation of temporal lobe epilepsy, and can potentially show characteristics of brain topology conducive to temporal lobe epilepsy pathophysiology, which includes seizure onset. Quaran et al. [43] showed that differences between control groups and patients in graph theory metrics showed a deviation from a small world network architecture. In theta band, epilepsy patients showed showed more of an orderly network, while in the alpha band, patients moved toward a random network. Haneef et al. [44] showed several possible biomarkers have been studied for identifying seizure. They note for localization, graph theory measures of centrality, betweenness centrality, outdegree, and graph index complexity show potential, and for prediction of seizure frequency, measures of synchronizability have shown the most potential.
There has also been significant research combining graph theory, machine learning, and classification. Ketkar et al. [45] showed the performance of various graph classification algorithms, including walk-based graph kernels, Subdue CL, FSG+SVM, FSG+AdaBoost, and DT- CLGBI. Petrosian et al. [46] used recurrent neural networks and signal wavelet decomposition to scalp and in- tracranial EEG readings to demonstrate the existence of a preictal state. Chisci et al. [47] proposed a novel way of auto-regressive modeling of EEG readings. Their method combines a least-square parameter estimator feature ex- traction with support vector machine for binary classification between preictal and interictal states. Subasi et al. [48] used binary classification based on decomposed frequency subbands using discreet wavelet trans- forms. They then extracted a set of statistical features to represent the distribution of wavelet coefficients. Then, principal components analysis, independent components analysis, or linear discriminant analysis was used for di- mensionality reduction. The features were then used as input to support vector machines for binary classi- fication. Shoeb et al. [49] presented a machine learning- based method for detecting the termination of seizure activity Their method successfully detected the end of 132 seizures within a few seconds of seizure termination. Yuan et al. [50] presents a detection method using a single hidden layer feed forward neural network. They note that nonlinear dynamics is a powerful tool for understanding brain electrical activities, and used nonlinear features extracted from EEG signals such as approximate entropy, Hurst exponents, and scaling exponent obtained with de- trended fluctuation analysis to train their neural network and characterize interictal and ictal EEGs. Their results indicate the differences of those nonlinear features between interictal and ictal EEGs are statistically significant. Rasekhi et al. [51] suggest a method involving combining twenty two linear univariate features to form a 132 dimensional feature space. After preprocessing and normalization, they use machine learning techniques for classification.
However, seizure detection and prediction is not limited to EEG data. Zijlmans et al. [52] observed ECG abnormalities in 26% of seizures, an increase in heart rate of at least 10 beats/minute in 73% of seizures, and in 23% of seizures the rate increase preceded both the electrographic and clinical onset. Using statistical classifier models, Greene et al. [53] used the combination of simultaneously-recorded electroencephalogram and electrocardiogram to detect neonatal seizures in newborns. Using a neuro-fuzzy inference system, Guler and Ubeyli [54] proposed a new method of seizure detection based on features extracted from electroencephalogram data using wavelet transform, and was trained with back propagation gradient descent method in combination with least squares. Kolsal et al. [55] state it is possible that heart rate variability could be used to predict seizures, and note from their study that heart rate variability during and before seizures revealed higher nLF and LF/HF ratio and lower nHF values demonstrating increased sympathetic activity. Hashimoto et al. [56] stated the fluctuation of the R-R interval of an electrocardiogram reflects the autonomic nervous function, an epileptic seizure may be predicted through monitoring heart rate variability data of patients with epilepsy. Their study showed that frequency heart rate variability features (LF and LF/HF) changed at least one minute before a seizure occurred in all studied seizure episodes. Osorio [57] demonstrated automated EKGbased seizure detection is feasible and has potential utility given its ease of acquisition, processing, and ergonomic advantages.
Graph Theory
Our analysis involves studying the various graph features and how they relate to the changing dynamics in the brain. Our algorithm uses dissimilarity of base case and test case graphs based on these features to identify seizure activity. While previous studies have focused only on node and link dissimilarity, we analyze these areas, as well as centrality, cycles, and connections. The purpose of this section is to identify the graph features used in our analysis, and define their meaning and interpretation.
The following graph features were used in our analysis to measure dissimilarity:
• Node Difference: Nodes in graph A not in graph B, Nodes in graph B not in graph A;
• Link Difference: Edges in graph A not in graph B, Edges in graph B not in graph A;
• Node Directed: Nodes in base case graph not in test case graph
• Link Directed: Edges in base case graph not in test case graph
• Inverted Node: Nodes in test case graph not in base case graph
• Inverted Link: Edges in test case graph not in base case graph
• Graph Centrality: Most influential vertices in base case graph not in graph base case graph;
• Degree Centrality: Difference in the number of links incident upon nodes in base case graph and test case graph;
• Number of Cycles (size Lambda): Difference in number of cycles size Lambda in base case graph and test case graph;
• Number of Cycles (size Mu): Difference in number of cycles size Mu in base case graph and test case graph;
• Number of Bi-connected Groups: Difference in number of Bi-connected components in base case graph and test case graph;
• Number of Strongly Connected Components: Difference in number of strongly connected components in base case graph and test case graph;
• Average Size of Strongly Connected Components: Difference in average size of strongly con- nected components in base case graph and test case graph;
• Average Clustering Coefficient: Difference in average of the local clustering coefficients of all vertices in base case graph and test case graph [58];
• Node Edge Betweenness Centrality: Nodes central in base case graph not in test case graph.
Analysis
Our analysis involved the use of 10 parameter sets, which are listed in Table 2, as well as 3 more parameter sets used for validation also listed in Table 2. The data was uniformly sampled at 250 Hz. All parameter sets used scalp EEG data in the 10-20 system from electrode channels F8 and FP2. Data acquisition was under standard humanstudies protocols from 41 temporal- lobe- epilepsy patients. Ages ranged from 4 to 57 years old. 36 datasets were from females, while 24 datasets were from males. The datasets range in length from 1.4 to 8.2 hours with an average of 4.4 hours. Forty datasets had seizures, and twenty had no event. At that point each parameter set listed in Table 2 was run on the 60 data sets using the algorithm described above. We measures success based on the number of true positives (TP) for known event data sets (Ev), yielding sensitivity of TP/Ev, and the number of true negatives (TN) for known non-event data sets (NEv), yielding specificity of TN/NEv. The goal is a similar sensitivity and specificity rate, and to minimizing the distance (D = prediction distance):
| Set ID | Dimensions | Symbols | Lag | Mu | Half Width | Window Size | Number Base Cases |
|---|---|---|---|---|---|---|---|
| P1 | 7 | 3 | 56 | 77 | 29 | 49812 | 12 |
| P2 | 7 | 3 | 47 | 77 | 29 | 49725 | 12 |
| P3 | 10 | 2 | 50 | 24 | 19 | 22320 | 12 |
| P4 | 10 | 2 | 50 | 52 | 19 | 22304 | 12 |
| P5 | 7 | 3 | 56 | 35 | 29 | 49699 | 12 |
| P6 | 8 | 3 | 70 | 22 | 28 | 49996 | 14 |
| P7 | 7 | 3 | 56 | 19 | 29 | 49721 | 12 |
| P8 | 7 | 3 | 56 | 21 | 29 | 49725 | 12 |
| P9 | 2 | 8 | 56 | 21 | 29 | 20000 | 12 |
| P10 | 7 | 3 | 56 | 77 | 29 | 49716 | 12 |
| V1 | 6 | 4 | 40 | 25 | 20 | 49000 | 15 |
| V2 | 4 | 6 | 48 | 40 | 30 | 35000 | 10 |
| V3 | 5 | 7 | 60 | 30 | 25 | 25000 | 8 |
Table 2: Parameter Sets.
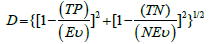 (3)
(3)
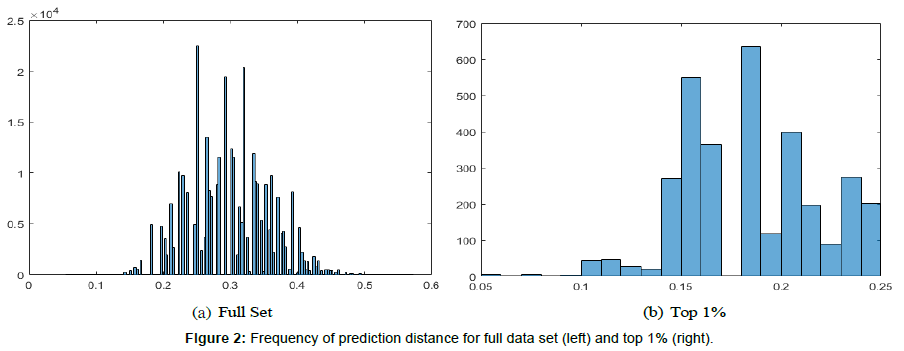
Every combination of the graph features listed above was run on the 10 parameter sets for all 60 data files. Each parameter set produced 32767 prediction distances corresponding to the combination of all features. We also produced data related to the graph properties listed in Table 2 for every graph produced. All parameter sets combined resulted in a true positive rate of 55%, a true negative rate of 25%, a false positive rate of 8%, and a false negative rate of 12%, yielding an accuracy of 80% and 87% precision. The mean prediction distance was 0.3 with a standard deviation of 0.06. Figure 2 shows the histogram of the prediction distances in the full data set, and the top 1%, which is described next.
The first step in our analysis involved taking the 325 lowest prediction distances from each parameter set and combining them to form a set of 3250 prediction distances. This data set represents the best performing 1% of prediction distances with their corresponding feature sets used for dissimilarity analysis from all ten parameter sets, resulting in a true positive rate of 59%, a true negative rate of 29%, a false positive rate of 5%, and a false negative rate of 7%, yielding an accuracy of 88% and 92% precision. The mean prediction distance was 0.18 with a standard deviation of 0.03. This represents a 67% improvement in mean prediction distance and a 50% improvement in variance over the full data set. We based the performance of each graph feature on the frequency of occurrence in the data set. Table 3 lists the results. The most frequently occurring dissimilarity feature is node inverted with 74% frequency. Within the range of 60%-69% was node, link inverted, and average strongly connected components. Within the range of 50%-59% was node directed and link directed. Within the range of 40%-49% was link, cycle size lambda, graph centrality, node edge betweenness centrality, and number of strongly connected components. The remaining features occurred less than 40% of the time. Clearly, the best results were achieved while using node inverted, node, link inverted, and average strongly connected components. However, in all of the top 1% of cases, no feature set contained only one dissimilarity measure. All feature sets contained two or more features.
| Feature | Frequency % | Frequency |
|---|---|---|
| Node | 2204 | 68 |
| Link | 1393 | 43 |
| Node Directed | 1882 | 58 |
| Link Directed | 1890 | 58 |
| Node Inverted | 2401 | 74 |
| Link Inverted | 2112 | 65 |
| Average Clustering Coefficient | 921 | 28 |
| Cycles Size Lambda | 1488 | 46 |
| Cycles Size Mu | 839 | 26 |
| Graph Centrality | 1481 | 46 |
| Degree Centrality | 1248 | 38 |
| Node Edge Betweenness Centrality | 1306 | 40 |
| Number of Strongly Connected Components | 1606 | 49 |
| Average Size Strongly Connected Components | 2066 | 64 |
| Number of Bi-connected Groups | 1252 | 38 |
Table 3: Frequency of Features.
In order to further identify best performing features, we combined the full data set from all ten parameters yielding 327670 prediction distances and dissimilarity features. We then performed stepwise regression on the data by treating the dissimilarity features as binary predictor variables and the prediction distance as the out- come variable. It is important to note the goal of per- forming stepwise regression was not to fit a regression equation or attempt predictive modeling. The nature of the data is nonlinear and chaotic, and as stated previously, typical statistical methods, such as regression, are ineffective. However, some insight about the data can be gained by performing stepwise regression. First, for the regression equation, the R squared value was 16.97% with a standard error of 0.05. It should be noted that the extremely low R squared value is partially due to the fact that the data set came from ten different parameter sets. When stepwise regression was performed on data from a single parameter set, the R squared value in- creased to 49%. Next, and most important for validation, we analyzed the T values of the individual dissimilarity features. For node, node directed, node inverted, link inverted, and average strongly connected components, the T values were large negative numbers. This indicates as a whole, those features resulted in a prediction distance that was less than the mean prediction distance. With the exception of link directed, these results coincide with the results from the frequency analysis of the best prediction distances. It should also be noted that the variance inflation factor for all dissimilarity measures was 1, indicating that there is no collinearity in the different dissimilarity features. Based on the results of the T values, we compare the mean prediction distances from test that used the dissimilarity feature to test that did not use the dissimilarity feature. Using node as a feature improved mean prediction distance by 11%, using node directed improved mean prediction distance by 4%, node inverted and link inverted both improved average prediction distance by 7%, and average strongly connected components improved prediction distance by 11%. These analysis were performed using Minitab 17. We also performed nonparametric test on the data to identify the best performers. Where the previous methods describe results based on mean, nonparametric test, such as Mood0s Median test, test the equality of medians from two or more populations [59]. Results from performing Mood0s Median test are as follows: The median prediction distance for test that used node as a dissimilarity measure improved results by 10%, node directed improved results by 3%, node inverted and link inverted improved results by 7%, and average number strongly connected components improved results by 10%. The remaining features had little or no impact, or a negative impact. The fact that the improvement from both mean and median are nearly identical is due to the approximate symmetry of the data distribution.
The next step of our analysis involved the frequency of cooccurrence. We evaluated how often pairs of dis- similarity features occurred together within the best per- forming 1% of prediction distances. The frequency of co-occurrence and percent of cooccurrence are listed in Tables 4 and 5 respectively. Of all the pairs, the following occurred together most often:
| S. No. | Feature | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Node | - | 917 | 1085 | 1196 | 1526 | 1428 | 740 | 1036 | 600 | 1075 | 851 | 891 | 1093 | 1450 | 868 |
| 2 | Link | - | - | 816 | 777 | 986 | 883 | 352 | 677 | 360 | 632 | 576 | 548 | 660 | 894 | 541 |
| 3 | Node Directed | - | - | - | 1101 | 1538 | 1211 | 465 | 792 | 402 | 728 | 509 | 760 | 908 | 1155 | 722 |
| 4 | Link Directed | - | - | - | - | 1542 | 1351 | 509 | 770 | 470 | 760 | 623 | 793 | 947 | 1207 | 711 |
| 5 | Node Inverted | - | - | - | - | - | 1556 | 624 | 1012 | 494 | 1008 | 801 | 820 | 1191 | 1507 | 941 |
| 6 | Link Inverted | - | - | - | - | - | - | 592 | 975 | 530 | 1095 | 904 | 754 | 1085 | 1277 | 792 |
| 7 | Average Clustering Coefficient | - | - | - | - | - | - | - | 592 | 921 | 436 | 386 | 469 | 471 | 727 | 426 |
| 8 | Cycles Size Lambda | - | - | - | - | - | - | - | - | 454 | 763 | 627 | 663 | 736 | 950 | 496 |
| 9 | Cycles Size Mu | - | - | - | - | - | - | - | - | - | 434 | 453 | 440 | 452 | 570 | 350 |
| 10 | Graph Centrality | - | - | - | - | - | - | - | - | - | - | 600 | 542 | 757 | 840 | 546 |
| 11 | Degree Centrality | - | - | - | - | - | - | - | - | - | - | - | 470 | 663 | 750 | 577 |
| 12 | Node Edge Betweenness Centrality | - | - | - | - | - | - | - | - | - | - | - | - | 643 | 870 | 430 |
| 13 | Number Strongly Connected Components | - | - | - | - | - | - | - | - | - | - | - | - | - | 1053 | 663 |
| 14 | Average Size Strongly Connected Components | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 829 |
| 15 | Number Bi-connected Groups | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
Table 4: Co-Frequency of Features.
| S. No. | Feature | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Node | - | 0.28 | 0.33 | 0.37 | 0.47 | 0.45 | 0.23 | 0.32 | 0.19 | 0.33 | 0.26 | 0.27 | 0.33 | 0.44 | 0.27 |
| 2 | Link | - | - | 0.25 | 0.24 | 0.30 | 0.27 | 0.11 | 0.21 | 0.11 | 0.2 | 0.18 | 0.17 | 0.20 | 0.28 | 0.17 |
| 3 | Node Directed | - | - | - | 0.34 | 0.47 | 0.37 | 0.14 | 0.24 | 0.12 | 0.22 | 0.16 | 0.23 | 0.28 | 0.35 | 0.22 |
| 4 | Link Directed | - | - | - | - | 0.47 | 0.42 | 0.16 | 0.24 | 0.15 | 0.23 | 0.19 | 0.24 | 0.29 | 0.37 | 0.22 |
| 5 | Node Inverted | - | - | - | - | - | 0.48 | 0.19 | 0.31 | 0.15 | 0.31 | 0.25 | 0.25 | 0.37 | 0.46 | 0.29 |
| 6 | Link Inverted | - | - | - | - | - | - | 0.18 | 0.192 | 0.31 | 0.15 | 0.31 | 0.25 | 0.25 | 0.36 | 0.46 |
| 7 | Average Clustering Coefficient | - | - | - | - | - | - | - | 0.18 | 0.3 | 0.16 | 0.34 | 0.27 | 0.23 | 0.33 | 0.39 |
| 8 | Cycles Size Lambda | - | - | - | - | - | - | - | - | 0.18 | 0.28 | 0.13 | 0.12 | 0.14 | 0.15 | 0.22 |
| 9 | Cycles Size Mu | - | - | - | - | - | - | - | - | - | 0.14 | 0.24 | 0.19 | 0.2 | 0.23 | 0.29 |
| 10 | Graph Centrality | - | - | - | - | - | - | - | - | - | - | 0.13 | 0.14 | 0.14 | 0.14 | 0.18 |
| 11 | Degree Centrality | - | - | - | - | - | - | - | - | - | - | - | 0.19 | 0.17 | 0.24 | 0.26 |
| 12 | Node Edge Betweenness Centrality | - | - | - | - | - | - | - | - | - | - | - | - | 0.15 | 0.2 | 0.23 |
| 13 | Number Strongly Connected Components | - | - | - | - | - | - | - | - | - | - | - | - | - | 0.2 | 0.27 |
| 14 | Average Size Strongly Connected Components | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0.32 |
| 15 | Number Bi-connected Groups | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
Table 5: Percent Co-Frequency of Features.
• node inverted and node;
• node inverted and node directed;
• node inverted and link directed;
• node inverted and average size strongly connected components;
• link inverted and node;
• link inverted and link directed;
• node and average size Strongly connected components.
All of these pairs occurred at a co-occurrence frequency greater than 40%. The combination of node and node inverted, node and link inverted, and node and average size strongly connected components improved mean pre- diction distance by 15%, node inverted and node directed and node inverted and link inverted improved mean prediction distance by 11%, node inverted and link directed and link inverted and link directed both improved mean prediction distance by 7%, and node inverted and aver- age size strongly connected components improved mean prediction distance by 15%.
Validation
In order to validate our results, we ran three more parameter sets. These sets were specifically picked in order to not duplicate any parameters used in the previous ten test sets. Validation was achieved by testing the improvement in prediction distance using node, node directed, node inverted, link inverted, and average number strongly connected components versus prediction distances not using those dissimilarity features. All features were tested individually and as a whole. All individual dissimilarity features showed improvement in mean pre- diction distance when used versus not used. The average improvement was 8.5%. When all features were used together, there was a 13.3% improvement of mean prediction distance.
Discussion
We have presented three metrics for judging the dis- similarity measures that produce the best results. First, we look for the most frequently occurring dissimilarity measures used in the best 1% of prediction distances. Second, we look at what dissimilarity measures produce prediction distances that are significantly lower than the mean prediction distance. Third, we look at what dissimilarity measures have a lower median prediction distance when used versus not used.
Our first step was to evaluate the frequency analysis of graph features. Our results indicate the graph features that most commonly occur within the best per- forming prediction distances are node inverted, node, link inverted, average strongly connected components, node directed, link directed, link, cycle size lambda, graph centrality, node edge betweenness centrality, and number of strongly connected components. All these features occurred with more than 40% frequency, and by limiting future test to only these features, we reduce our computational load by 27%. If we further narrow the scope, and consider frequent as occurring more often than not (at least 50%), we are left with node inverted, node, link inverted, average strongly connected components, node directed and link directed. Limiting future test to only these features will reduce computational load by 60%, and result in an average improvement in prediction distance by 8%. Further evaluation shows that these sets of features represent 1.7% of the top 1% best prediction distances. As previously noted, we chose parameter sets that historically performed well, performed average, as well as some random parameter sets. We checked to ensure the most frequent 1.7% of the top 1% did not all come from the best performing parameter sets, and found that was not the case.
Next, we analyzed the T values produced for each dissimilarity feature by performing stepwise regression. Results indicate that when node, node directed, node inverted, link inverted, and average strongly connected components are used in an analysis, the resulting prediction distance is significantly lower than the mean prediction distance for the entire data set.
Finally, by performing Moodrs Median test, we are able to judge which dissimilarity features produce a lower median prediction distance when used. Results indicate these were node, node directed, node inverted, link in- verted, and average number strongly connected compo- nents.
When combined, these tests give the overall best features to use when evaluating graph dissimilarity. We consider the frequency test as T1, mean test as T2, and median test as T3. The best features are those who in- tersect the sets produced from all test:
BestFeatures = T 1 ∩ T 2 ∩ T 3 (4)
After comparison, we find the best features are node, node directed, node inverted, link inverted, and average number strongly connected components. While link directed was common to some of the test, it was not common to all three, and was therefore removed.
After identifying the best performing dissimilarity features, we analyzed what combinations of these features occurred together most often. For this test we only considered combinations formed in the best 1% of prediction distances. We found node and node directed occur together at a frequency of 33%, and improved prediction distance by 15%. Node and node inverted occur together at a frequency of 47%, and improved prediction distance by 15%. Node and link inverted occur at a frequency of 45%, and improved prediction distance by 15%. Node and average number strongly connected components occur at a frequency of 44%, and improved prediction distance by 15%. Node directed and node inverted occurs at a frequency of 47%, and improved pre- diction distance by 11%. Node directed and link inverted occur at a frequency of 37%, and improved prediction distance by 7%. Node directed and average number strongly connected components occur at a frequency of 35%, and improved prediction distance by 7%. Node inverted and link inverted occur at a frequency of 48%, and improved prediction distance by 11%. Node inverted and average number strongly connected components occur at a frequency of 46%, and improved prediction distance by 15%. Link inverted and average number of strongly connected components occurs at a frequency of 36%, and improved prediction distance by 7%. Based on these findings the average percent frequency is 41.8% with a standard deviation of 5.8. Because none of these frequencies would be considered outliers, we assume all pairs of features are significant. When all these features were used together, the mean prediction distance was 25 which was a 24% improvement over the prediction distances as a whole.
Finally, results were validated using three parameter sets picked at random. These parameter sets did not use any parameters used in the previous test. Results of the validation check indicate similar results as were found in initial test.
Future Work
Our future work related to graph dissimilarity features is three fold. First, further validation is needed to ensure the accuracy of what we consider the best performing graph features. This can only be achieved by testing the various graph features on more parameter sets, and evaluating these test as described earlier. Further, more parameter sets should be run using only the graph features we consider best performers, and statistical validation of mean prediction distance should be evaluated to verify significant improvement using these features. Second, these test should also evaluate the co-occurrence frequency of parameter sets as described earlier, and at- tempt to further identify/validate the best subsets of graph dissimilarity features. Last, as mentioned earlier, significant research has been proposed to model the human brain using graph and network theory. Our algorithm uses phase space graphs to represent the changing dynamics within the brain. Further research should con- sider the meaning of dissimilarity measures we observe to be non-frequent. A dissimilarity measure being non frequent in our evaluation does not necessarily imply those graph features are common or not common, but that they remain static throughout phase space reconstruction. Further research should consider the implications of these results.
Conclusion
A reliable algorithm is needed to predict and detect the onset of epileptic seizures. However, realistic implementation of such an algorithm requires not only accuracy, but also minimal computational complexity. This paper serves as a stepping stone for future works. By evaluating the performance of dissimilarity measures, we now have a better understanding of what graph features to use when evaluating the phase space formed by EEG data to achieve better accuracy, and what graph features not to use to reduce computational complexity.
References
- Epilepsy Foundation of Michigan (2011) United States.
- Hively LM, Protopopescu VA (2003) Channel consistent forewarning of epileptic events from scalp EEG. IEEE Transactions on Biomedical Engineering 50: 584-593.
- Hively LM, McDonald JT, Munro N, Cornelius E (2013) Forewarning of epileptic events from scalp EEG. Biomedical Sciences and Engineering Conference. Oak Ridge, USA.
- Hively LM, Clapp NE, Stuart Daw C, Lawkins WF (1999) Epileptic seizure prediction by non-linear methods. Lockheed Martin Enrgy Syst Inc.
- Hively LM, Gailey PC, Protopopescu VA (1999) Detecting dynamical change in nonlinear time series. Physics Letters A 258: 103-114.
- Hively LM, Protopopescu VA, Gailey PC (2000) Timely detection of dynamical change in scalp EEG signals. Chaos An Interdisciplinary Journal of Nonlinear Science 10: 864-875.
- Hively LM, Clapp NE, Protopopescu VA, Joseph J, Merican CE (2000) Epileptic seizure forewarning by nonlinear techniques 1-4.
- Hively LM, Clapp NE, Daw CS, Lawkins WF, Eisenstadt ML (1995) Nonlinear Analysis of EEG for Epileptic Seizures. Oak Ridge National Laboratory 1-45.
- Protopopescu VA, Hively LM, Gailey PC (2001) Epileptic event forewarning from scalp EEG. Journal of Clinical Neurophysiology 18: 223-245.
- Ding M, Ditto WL, Pecora LM, Spano ML (1999) Proceedings of the 5th Experimental Chaos Conference, Orlando, Florida.
- Manuca R, Savit R (1996) Stationarity and nonstationarity in time series analysis. Physica D: Nonlinear Phenomena 99: 134-161.
- Manuca R, Casdagli MC, Savit RS (1998) Nonstationarity in epileptic EEG and implications for neural dynamics. Mathematical biosciences 147: 1-22.
- Elger CE, Lehnertz K (1998) Seizure prediction by nonlinear time series analysis of brain electrical activity. European Journal of Neuroscience 10: 786-789.
- Elbert T, Ray WJ, Kowalik ZJ, Skinner JE, Graf KE, et al. (1994) Chaos and physiology deterministic chaos in excitable cell assemblies. Physiological Reviews 74: 1-47.
- Iasemidis LD, Sackellares JC (1991) The evolution with time of the spatial distribution of the largest Lyapunov exponent on the human epileptic cortex. Measuring chaos in the human brain 49-82.
- Iasemidis LD, Sackellares JC (1996) Review: Chaos Theory and Epilepsy. The Neuroscientist 2: 118-126.
- Lopes da Silva F, Blanes W, Kalitzin SN, Parra J, Suffczynski P, et al. (2003) Epilepsies as dynamical diseases of brain systems: basic models of the transition between normal and epileptic activity. Epilepsia 44: 72-83.
- Scheffer M, Bascompte J, Brock WA, Brovkin V, Carpenter SR, et al. (2009) Early-warning signals for critical transitions. Nature 461: 53-59.
- Mormann F, Andrzejak RG, Elger CE, Lehnertz K (2007) Seizure prediction: the long and winding road. Brain 130: 314-333.
- Mormann, Florian, et al. (2016) Seizure prediction: making mileage on the long and winding road. Brain 139: 1625-1627.
- Lehnertz K (2008) Epilepsy and nonlinear dynamics. Journal of biological physics 34: 253-266.
- Winterhalder M, Maiwald T, Voss HU, Aschenbrenner-Scheibe R, Timmer J, et al. (2003) The seizure prediction characteristic a general framework to assess and compare seizure prediction methods. Epilepsy and Behavior 4: 318-325.
- Andrzejak RG, Chicharro D, Elger CE, Mormann F (2009) Seizure prediction any better than chance?. Clinical Neurophysiology 120: 1465-1478.
- Snyder DE, Echauz J, Grimes DB, Litt B (2008) The statistics of a practical seizure warning system. Journal of neural engineering 5: 392-401.
- Hively LM, Protopopescu VA, Munro NB (2005) Enhancements in epilepsy forewarning via phase space dissimilarity. Journal of clinical neurophysiology 22: 402-409.
- Brian L, Echauz J (2002) Prediction of epileptic seizures. The Lancet Neurology 1: 22-30.
- Takens F (1981) Detecting strange attractors in turbulence. Dynamical systems and turbulence Warwick 1980. Springer Berlin Heidelberg.
- Viglione, Walsh (1975) Proceedings Epileptic Seizure Prediction. Electroencephalogr Clin Neurophysiol 39: 43536.
- Wackermann J, Allefeld C (2009) State space representation and global descriptors of brain electrical activity. Electrical neuroimaging, Cambridge University Press.
- Mirowski, Madhavan, LeCun, Kuzniecky (2009) Classification of patterns of EEG synchronization for seizure prediction. International Federation of Clinical Neurophysiology Elsevier Ireland.
- Stam CJ, Reijneveld JC (2007) Graph theoretical analysis of complex networks in the brain. Nonlinear Biomedical Physics 1: 1753-4631.
- Feldwisch-Drentrup H, Schelter B, Jachan M, Timmer JJ, Schulze-Bonhage A (2010) Joining the benefits: Combining epileptic seizure prediction methods. Epilepsia 51: 1528-1167.
- Zijlmans M, Jiruska P, Zelmann R, Leijten FS, Jefferys JG, et al. (2012) High Frequency Oscillations as a New Biomarker in Epilepsy. Ann Neurol 71: 169-78.
- Raghunathan S, Jaitli A, Irazoqui PP (2011) Multi Stage Seizure Detection Techniques Optimized for Low Power Hardware Platforms. Epilepsy and Behavior 22: S 61-S 68.
- Mirowski, Madhavan, LeCun, Kuzniecky (2008) Classification of Patterns of EEG Synchronization for Seizure Prediction. American Epilepsy Society. IEEE Workshop on Machine Learning for Signal Processing.
- Mirowski, LeCun, Madhavan D, Kuzniecky R (2008) Comparing SVM and Convolutional Networks for Epileptic Seizure Prediction from Intracranial EEG. IEEE Workshop on Ma- chine Learning for Signal Processing, Cancun, Mexico.
- Yuan Y, Mandic DP, Yue L (2008) Comparison Analysis of Embedding Dimension between Normal and Epileptic EEG Time Series. The Journal of Physiological Sciences Advance Publication J- STAGE.
- Astolfi L, de Vico Fallani F, Cincotti F, Mattia D, Marciani MG (2007) Imaging functional brain connectivity patterns from high resolution EEG and fMRI via graph theory. Psychophysiology 44: 880-893.
- D’Alessandro M, Esteller R, Vachtsevanos G, Hinson A, Echauz J (2003) Epileptic seizure prediction using hybrid feature selection over multiple intracranial EEG electrode contacts: a report of four patients. IEEE Transactions on Biomedical Engineering 50: 603-615.
- Adeli H, Ghosh-Dastidar S, Dadmehr N (2007) A wavelet chaos methodology for analysis of EEGs and EEG subbands to detect seizure and epilepsy. IEEE Transactions on Biomedical Engineering 54: 205-211.
- Firpi Hiram, Goodman ED, Echauz J (2007) Epileptic seizure detection using genetically programmed artificial features. IEEE Transactions on Biomedical Engineering 54: 212-224.
- Chiang S, Haneef Z (2014) Graph theory findings in the pathophysiology of temporal lobe epilepsy. Clinical Neurophysiology 125: 1295-1305.
- Quraan, Maher A (2013) Altered resting state brain dynamics in temporal lobe epilepsy can be observed in spectral power functional connectivity and graph theory metrics. PloS one 8: e68609.
- Haneef Z, Chiang S (2014) Clinical correlates of graph theory findings in temporal lobe epilepsy. Seizure 23: 809-818.
- Ketkar NS, Holder LB, Cook DJ (2009) Empirical Comparison of Graph Classification Algorithms. IEEE Symposium on Computational Intelligence and Data Mining.
- Petrosian, Arthur (2000) Recurrent neural network based pre- diction of epileptic seizures in intra and extracranial EEG. Neurocomputing 30: 201-218.
- Chisci L (2010) Real-time epileptic seizure prediction using AR models and support vector machines. IEEE Transactions on Biomedical Engineering 57: 1124-1132.
- Subasi A, Gursoy MI (2010) EEG signal classification using PCA, ICA, LDA and support vector machines. Expert Systems with Applications 37: 8659-8666.
- Shoeb A, Kharbouch A, Soegaard J, Schachter S, Guttag J (2011) A machine-learning algorithm for detecting seizure termination in scalp EEG. Epilepsy and Behavior 22: S36-43.
- Yuan Q, Zhou W, Li S, Cai D (2011) Epileptic EEG classification based on extreme learning machine and nonlinear features. Epilepsy research 96: 29-38.
- Rasekhi J, Mollaei MR, Bandarabadi M, Teixeira CA, Dourado A (2013) Preprocessing effects of 22 linear univariate features on the performance of seizure prediction methods. Journal of neuroscience methods 217: 9-16.
- Zijlmans M, Flanagan D, Gotman J (2002) Heart Rate Changes and ECG Abnormalities During Epileptic Seizures: Prevalence and Definition of an Objective Clinical Sign. Epilepsia 43: 847-854.
- Greene BR, Boylan GB, Reilly RB, de Chazal P, Connolly S (2007) Combination of EEG and ECG for improved automatic neonatal seizure detection. International Federation of Clinical Neurophysiology 118: 1348-1359.
- Guler I, Ubeyli ED (2004) Application of adaptive neurofuzzy inference system for detection of electrocardiographic changes in patients with partial epilepsy using feature extraction. Expert Systems with Applications 27: 323-330.
- Kolsala E, Serdaroğlu A, Cilsal E, Kula S, Soysal AŞ, et al. (2014) Can heart rate variability in children with epilepsy be used to predict seizures?. Seizure 23: 357-362.
- Hashimoto H, Fujiwara K, Suzuki Y, Miyajima M, Yamakawa T, et al. (2013) Heart rate variability features for epilepsy seizure prediction. Asia-Pacific Signal and Information Processing Association Annual Summit and Conference.
- Osorio (2014) Automated Seizure Detection Using EKG. International Journal of Neural Systems 24: 1450001.
- Watts DJ, Strogatz S (1998) Collective dynamics of small-world networks. Nature 393: 440-442.
- Fligner, Michael A, Rust Steven W (1982) A modification of Mood’s median test for the generalized Behrens-Fisher problem. Biometrika 69: 221-226.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi