Research Article, J Chem Appl Chem Eng Vol: 1 Issue: 1
Formulation of Simple Electrolytic Redox Systems According to GATES/GEB Principles
Anna Maria Michalowska-Kaczmarczyk1, Aneta Spórna-Kucab2 and Tadeusz Michalowski2*
1Department of Oncology, The University Hospital in Cracow, 31-501 Cracow, Poland
2Department of Analytical Chemistry, Technical University of Cracow, 31-155 Cracow, Poland
*Corresponding Author : Tadeusz Michalowski
Faculty of Chemical Engineering and Technology, Cracow University of Technology, Warszawska 24, 31-155 Cracow, Poland
Tel: +48126282035
E-mail: michalot@o2.pl
Received: October 04, 2017 Accepted: October 09, 2017 Published: October 15, 2017
Citation: Michalowska-Kaczmarczyk AM, Spórna-Kucab A, Michalowski T (2017) Formulation of Simple Electrolytic Redox Systems According to GATES/ GEB Principles. J Chem Appl Chem Eng 1:1 doi: 10.4172/2576-3954.1000105
Abstract
The linear combination f12 = 2�??f(O) – f(H) of elemental balances: f1 = f(H) for H, and f2 = f(O) for O is the basis to formulate the generalized electron balance (GEB) for electrolytic redox systems according to Approach II to GEB, realized within the generalized approach to electrolytic systems (GATES) as GATES/GEB. Together with charge balance (f0 = ChB) and K–2 elemental/core balances: f3,…,fK, the f12 completes the set of K balances needed for resolution of an electrolytic redox system, of any degree of complexity. For a nonredox system, a proper linear combination of f12 with f0, and fk = f(Yk) (Yk ≠ H, O; k=3,…,K) gives the identity, 0 = 0. Consequently, in nonredox systems, f12 is linearly dependent on f0,f3,…,fK, i.e., f12 is not the independent balance. This independency/dependency property of f12 distinguishes between redox and non-redox systems. In a redox system, a proper linear combination of f12+f0 with the balances for electron-non-active elements/cores gives the simpler form of GEB, where the species composed only of electron-non-active elements are not involved. The multipliers applied in the linear combinations are equal to the oxidation numbers for elements participating redox or non-redox system. This regularity is highly important in context of the fact that the ‘oxidation number’ was essentially a contractual concept. Within GATES/GEB, the terms: oxidation number, oxidant and reductant, stoichiometry, and equivalent mass are derivative/redundant concepts only; the roles of oxidants and reductants are not assigned a priori to individual components. All these concepts are illustrated on simple examples of redox D+T systems, with aqueous solutions of (S1) Br2, and (S2) HBrO as titrand D, and NaOH solution as titrant T.
Keywords: Electrolytic redox systems; Oxidation numbers; GATES/GEB
Introduction
The Generalized Approach to Electrolytic Systems (GATES) [1-13] is the best thermodynamic approach to equilibrium and metastable electrolytic systems of any degree of complexity, where all necessary, physicochemical knowledge on the systems tested can be involved. The GATES is applicable, among others, (a) to mathematical modelling of redox and non-redox electrolytic systems, (b) in choice of optimal a priori conditions of chemical analyses, and (c) in gaining the chemical information invisible in real experiments. The modelling of redox systems is based on general laws of elements and charge preservation, related to closed electrolytic systems composed of condensed (liquid or liquid+solid) phases, separated from the environment by diathermal walls.
The terms: components and species are distinguished. The species in aqueous systems are considered in their natural form, i.e. as hydrates 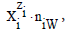 where zi (zi = 0, ± 1, ± 2,…) is the charge of
where zi (zi = 0, ± 1, ± 2,…) is the charge of 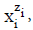 expressed in elementary charge unit e = F/NA (F – Faraday constant, NA – Avogadro’s constant), and niW (≥ 0) is the mean number of water (W = H2O) molecules attached to
expressed in elementary charge unit e = F/NA (F – Faraday constant, NA – Avogadro’s constant), and niW (≥ 0) is the mean number of water (W = H2O) molecules attached to 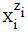 . The known chemical formulas of the
. The known chemical formulas of the 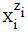 and their respective external charges provide the information necessary/sufficient to formulate the respective balances [3], for elements or cores. A core is a cluster of elements with defined composition, expressed by its chemical formula, structure and external charge, that remains unchanged in a system considered, realized during the titration.
and their respective external charges provide the information necessary/sufficient to formulate the respective balances [3], for elements or cores. A core is a cluster of elements with defined composition, expressed by its chemical formula, structure and external charge, that remains unchanged in a system considered, realized during the titration.
The titration is a dynamic procedure, where V mL of titrant T, containing a reagent B (C mol/L), is added into V0 mL of titrand D, containing a substance A (C0 mol/L). An advance of the titration B(C,V) ⟹ A(C0,V0), denoted briefly as B ⟹ A, is characterized by the fraction titrated
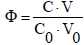 (1)
(1)
that introduces a kind of normalization (independence on V0 value) for titration curves, expressed by pH = pH(Φ), and E = E(Φ) for potential E [V] expressed in SHE scale. In further sections we formulate the balances for redox systems containing one, two or three electron-active elements in redox systems (aqueous media), where the complete set of expressions for independent equilibrium constants, interrelating concentrations of different species, is involved. The redox systems are modeled according to GATES/GEB principles.
In the notation applied here, N0j (j=1,2,…,J) is the number of molecules of the component of j-th kind, including water, forming a static or dynamic D+T system, from titrand D and titrant T composed separately. The D+T system thus obtained involves N1 molecules of H2O and Ni species of i-th kind, 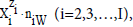 denoted briefly as
denoted briefly as 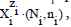 where ni≡niW≡niH2O. Molar concentration of the species
where ni≡niW≡niH2O. Molar concentration of the species 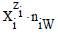 is denoted as
is denoted as 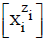 . Except the pH = pH(Φ), and E = E(Φ) relationships, the D+T systems are represented graphically by speciation curves
. Except the pH = pH(Φ), and E = E(Φ) relationships, the D+T systems are represented graphically by speciation curves 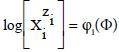 .
.
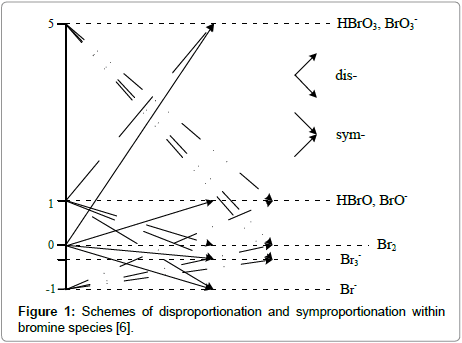
We consider here two systems with bromine as one electron-active disproportionating element [4,6,10]. These properties are appropriate for the elements that form compounds and species at three or more oxidation degrees. In particular, bromine (Br) forms the species on five oxidation degrees (–1, –1/3, 0, 1, 5), (Figure 1), e.g. 0 (for Br2) and 1 (for HBrO or NaBrO) ϵ (–1, 5). There are possible transitions between different bromine species, associated with changes of the oxidation states of this element, (Figure 1).
Figure 1: Schemes of disproportionation and symproportionation within bromine species [6].
We consider first two D+T systems: (S1) NaOH → Br2 and (S2) NaOH → HBrO. In the system S1, V0 mL of D is composed of Br2 (N01 molecules) + H2O (N02molecules), and V mL of T is composed of NaOH (N03 molecules) + H2O (N04 molecules). In the system S2, V0 mL of D is composed of HBrO (N01 molecules) + H2O (N02molecules), and V mL of T is composed of NaOH (N03 molecules) + H2O (N04 molecules).
In both systems (S1, S2), the D+T mixture involves the following species:
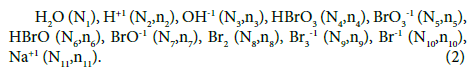
Let us assume that V mL of the titrant T is added into V0 mL of the titrand D, up to a given point of the titration, and V0+V mL of D+T mixture is obtained. Molar concentration (C0) of the solute X in D (i.e. X = Br2 or HBrO) is involved in relation
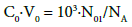 (3)
(3)
and molar concentration (C) of the solute Y = NaOH in T is involved in relation
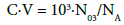 (4)
(4)
Molar concentrations 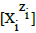 of the species in the D+T mixture are involved in the relations
of the species in the D+T mixture are involved in the relations
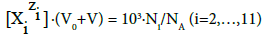 (5)
(5)
At V=0, the related system is limited to D, i.e. (S1) Br2 (C0) solution, or (S2) HBrO (C0) solution, and we have
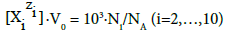 (6)
(6)
In this paper, the redox systems will be formulated first according to the Approach II to GEB. Some problems involved with these systems will be discussed in details, and then generalized on more complex systems.
Formulation of the redox systems
The system S1
V0 mL of D is composed of Br2 (N01 molecules) + H2O (N02molecules), and V mL of T is composed of NaOH (N03 molecules) + H2O (N04 molecules). The balances related to the D+T mixture are as follows:
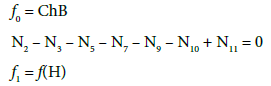 (7)
(7)
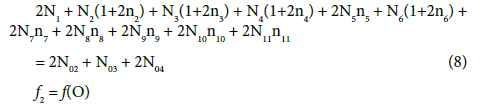
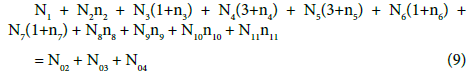
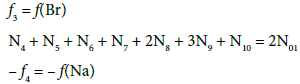 (10)
(10)
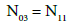 (11)
(11)
Note, for example, that N4 molecules (z4=0) of HBrO3∙n4H2O involve: N4(1+2n4) atoms of H, N4(3+n4) atoms of O, and N4 atoms of Br. From Equations 8 and 9 we have
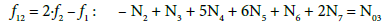 (12)
(12)
From Equations 7, 11 and 12
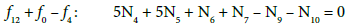 (13)
(13)
Applying the atomic number ZBr (= 35) for Br, from Equations 10 and 13 we have
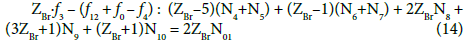
Note, for example, that f4 = f(Na) ↔ f(Na) = f4 ↔ –f4 = – f(Na).
The system S2
In the system S2, the set (2) of the species is identical as in the system S1. Applying similar notation, we assume that V0 mL of D is composed of HBrO (N01 molecules) + H2O (N02molecules), and V mL of T is composed of NaOH (N03 molecules) + H2O (N04 molecules). The f0 = ChB in the system S2 is identical with Equation 7, and –f4 = –f(Na) is as in Equation 11. Then after formulation of the balances for the related D+T mixture:
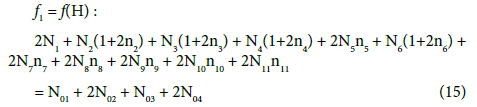
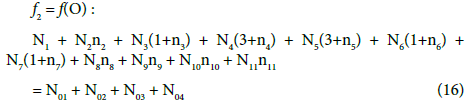
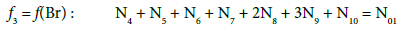 (17)
(17)
we have here, by turns,
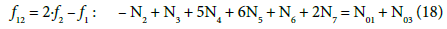
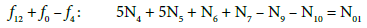 (19)
(19)
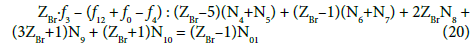
In principle, the numbers N01 and N02 of the molecules composing the system S2 and the numbers Ni of the species in the related D+T mixture are different than that in the system S1.
Components versus species
Br2 and H2O forming D, and NaOH and H2O forming T, are components of the system S1; HBrO and H2O forming D, and NaOH and H2O forming T, are components of the system S2. The species in (2) are present in the D+T systems (S1 and S2) thus formed. All components are uncharged entities, whereas the species are formed by charged (cations, anions) or uncharged (molecules) entities.
The systems S1 and S2 in terms of molar concentrations
For the systems S1 and S2, from Equations 5 and 7 we have
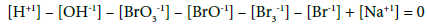 (7a)
(7a)
For the system S1, from Equations 3 – 5, 10, 11 and 13, we have:
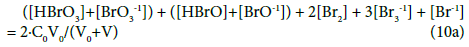
[Na+1] = CV/(V0+V) (11a)
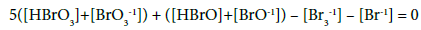 (13a)
(13a)
Equations 10a and 11a are termed as concentration balances, obtained from elemental balances 10 and 11, and Equation 13a is the shorter form of GEB, expressed in terms of concentrations. The relation 11a can be immediately introduced into Equation 7a; then we get
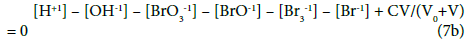
Equations 7b, 10a and 13a form the complete set of balances related to the system S1.
For the system S2, from Equations 3–5, 17 and 19, we obtain the balances:
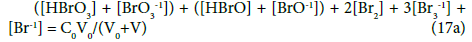
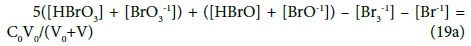
completed by the balance 7b.
We can also refer to static systems, formed by C0 mol/L solutions of: (S1) Br2, (S2) HBrO. These solutions are identical with the titrand D in the related systems S1 and S2. The balances for the static systems are obtained assuming V=0 in Equations 7b and 10a for S1, or in Equations 7b, 17a and 19a for S2. Equation 13a is identical for the dynamic and static systems with C0 mol/L Br2 in D; Equation 7b is identical in S1 and S2.
Some Detailed Remarks
The remarks related to water molecules
The numbers: N1, ni (i=2,…,I), and N0j related to W=H2O molecules (i.e., free W as the species, W in hydrated species, and W as components) are cancelled within f12. In other words, I – 1 kinds of the species 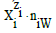 are involved in equations related to the system. All ni = niW values are virtually unknown – even for
are involved in equations related to the system. All ni = niW values are virtually unknown – even for 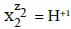 [14] in aqueous media, and depend on ionic strength (I) of the solution. The species
[14] in aqueous media, and depend on ionic strength (I) of the solution. The species 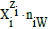 with different niW values are considered equivalently. Also the
with different niW values are considered equivalently. Also the 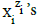 with different numbers of H2O molecules involved,
with different numbers of H2O molecules involved,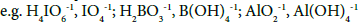 are considered equivalently, i.e., as the same species in this medium [11].
are considered equivalently, i.e., as the same species in this medium [11].
The Approach I to GEB
In C0 mol/L Br2 solution (D in the system S1), bromine is the only electron-active element, considered as the carrier of its own, bromine electrons. One atom of Br has ZBr bromine electrons, and then one molecule of Br2 has 2ZBr bromine electrons, i.e., N01 molecules of Br2 involve 2ZBr∙N01 bromine electrons. The oxidation degree x of an atom in a simple species, such as ones formed here by bromine, is calculated on the basis of known oxidation degrees: +1 for H, and –2 for O, and external charge of this species. We have, by turns, the relations: 1∙1 + 1∙x + 3∙(–2) = 0 → x= 5 for HBrO3; 1∙x + 3∙(–2) = –1 → x = 5 for BrO3-1; 1∙1 + 1∙x + 1∙(–2) = 0 → x = 1 for HBrO; … ; 3∙x = –1 → x = –1/3; 1∙x = –1 → x = –1 for Br-1.
The oxidation degree is the net charge resulting from the presence of charge carriers, inherently involved in an atom: protons in nuclei and orbital electrons, expressed in elementary charge units as: +1 for protons, and –1 for electrons. The number y of bromine electrons in one molecule of HBrO3 is calculated from the formula: ZBr∙(+1) + y∙(–1) = 5, i.e., bromine involves y = ZBr–5 bromine electrons, etc. On this basis, we state that [10]:
N4 species HBrO3∙n4H2O involve (ZBr–5)∙N4 bromine electrons;
N5 species BrO3-1∙n5H2O involve (ZBr–5)∙N5 bromine electrons;
N6 species HBrO∙n6H2O involve (ZBr–1)∙N6 bromine electrons;
N7 species BrO-1∙n7H2O involve (ZBr–1)∙N7 bromine electrons;
N8 species Br2∙n8H2O involve 2ZBr∙N8 bromine electrons;
N9 species Br3-1∙n9H2O involve (3ZBr+1)∙N9 bromine electrons;
N10 species Br-1∙n10H2O involve (ZBr+1)∙N10 bromine electrons;
N01 molecules of Br2 involved 2ZBr∙N01 bromine electrons.
Equivalence of the Approaches I and II to GEB
Balancing of bromine electrons gives here Equation 14 (system S1), and then
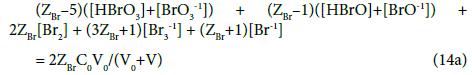
In the system S2, N01 molecules of HBrO brings (ZBr–1)∙N01 bromine electrons, and from the related balancing we obtain Equation 20, and then
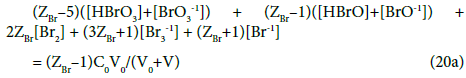
The equations: 14 → 14a and 20 → 20a are examples of formulation of GEB according to Approach I to GEB. The GEB formulation presented in the previous section 5.2, and considered as the Approach I to GEB in the related systems (S1 and S2), gives the Equations 14a and 20a equivalent with equations 14 and 20; this means that the interdependence
Approach I to GEB ⟺ Approach II to GEB (21)
is true [10].
Other equivalent forms of GEB
The f12 (Equation18) and other combinations of f12 with f0, f3 and f4 (Equations 7,17,11) have full properties of GEB for the system S1. Note that the GEB obtained for the system S2 from f12 (Equation 12) has the form
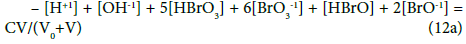
The GEB obtained for the system S2 from f12 (Equation 18) has the form
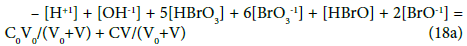
One can also state that f12 (Equation 12 ) and other combinations of the f12 with f0, f3 and f4 (Equations 7,10,11) have full properties of GEB for the system S1. For example, we have:
(f12 + f0 + f3 – f4)/2 : 3(N4 + N5) + N6 + N7 + N8 + N9 = N01 → (22)
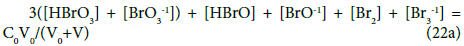
For the system S2, the relations derived for (f12 + f0 + f3 – f4)/2 are identical with equations 22 and 22a.
Minimal number of constituents as a criterion of GEB simplicity
As were stated above, f12, f12+f0 and any linear combination of f12 with f0,f3,…,fI related to the system in question, i.e.,

have full properties of GEB. An interesting matter is here the selection of such ak coefficients where the linear combination contains the minimal number of constituents (species, components), after all cancellations done in (23). We calculate the summary number Sm = Im + Jm of constituents in Equation (23), where Im – the number of species, and Jm – the number of components. We refer here to the systems S1 and S2.
For the system S1 we have: Sm1 = 6+0 = 6 from (13a), Sm2 = 7+1 = 8 from (14a), Sm3 = 6+1 = 7 from (12a), Sm4 = 6+1 = 7 from (22a). For the system S2 we have: Sm1 = 6+1 = 7 from (19a), Sm2 = 7+1 = 8 from (20a), Sm3 = 6+2 = 8 from (18a), Sm4 = 6+1 = 7 from (22a). Then we have minimal (Sm)min = 6 for the system S1, and (Sm)min = 6 for the system S2. The linear combinations with smaller number Sm are not obtainable for the systems S1 and S2 and then (Sm)min > 0 in both instances, i.e., the combination (23) is not transformed there to identity 0 = 0. Note that Im’s in (12a) and (18a) involve 2 components related to the species (H+1∙n2W, OH-1∙n3W) and 1 compound (NaOH), related to the entities composed only of ‘fans’: H, O, Na.
Electron-active and electron-non-active elements
In the systems S1 and S2, we have only one electron-active element: bromine (Br), as (S1) Br2 or (S2) HBrO, i.e. as the components on the intermediary oxidation states: 0 in (S1), and +1 in (S2), able to disproportionation in aqueous media, see Figure 1. The Br2 in S1 or HBrO in S2 are characterized as ‘distributors’ of electrons in the related systems. Note that Br2 and HBrO do not oxidize water molecules, i.e., products of H2O oxidation do not exist (are not formed) there as species. Hydrogen (H), oxygen (O) and sodium (Na) are electron-non-active elements in the systems S1 and S2.
In all instances, the (partial) linear combination f12+f0 is applied for cancellation purpose; –N2+N3 = –(N2–N3) are cancelled within the sum f12+f0 related to redox and non-redox systems.
Oxidation number, oxidant and reductant as the redundant terms
The GEB related to the system S1 with Br2 (C0) and expressed by Equation 13a, obtained according to Approach II to GEB, can be rewritten as follows:
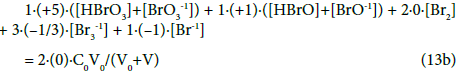
Whereas the GEB related to the system S2 with HBrO (C0) and expressed by Equation 19a, obtained according to Approach II to GEB, can be rewritten as follows:
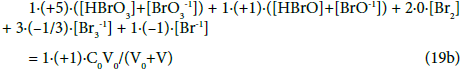
As we see, in the balances obtained from f12+f0, the oxidation numbers in particular Br-species are equal to (or involved with) the coefficient/multiplier at the concentration of the corresponding species with electron-active element (here: Br), and in the component (Br2 or HBrO) or bromine species. If the species or component involves more atoms of an electron-active element, then the coefficient is equal to the product of the related numbers; e.g. –[Br3-1] = (–1)[Br3-1]= 3∙(–1/3)∙ [Br3-1] in Equation 13a or 19a, where 3 = number of Br-atoms, –1/3 = oxidation number of Br in Br3-1.
Concluding,
(1) the formulation of GEB according to Approach II to GEB, i.e., where f12 is calculated, needs none prior knowledge of the oxidation states (oxidation numbers) of all elements participating the system S1 or S2, i.e., Br, H, O; it means that the oxidation state (oxidation number) is the derivative concept within GATES/GEB;
(2) the terms: oxidant and reductant are not distinguished, i.e., not ascribed a priori to particular components and species in electrolytic systems, considered according to GATES/GEB principles, with GEB obtained according to Approaches I and II to GEB; full ‘democracy’ in this respect is assumed.
Comparison of the Approaches I and II to GEB
The Approach I to GEB [10], named as the ‘short’ version of GEB, needs the knowledge of oxidation numbers for all elements in all the species participating the system considered. This knowledge is not required in the Approach II to GEB; the known composition (chemical formula) of a species and its external charge are quite sufficient for this purpose. This property of the Approach II to GEB is of capital importance, particularly in context with complex organic substances/compounds and species involved in redox equilibia. Thus, the Approach II to GEB offers very essential advantages, when compared with the Approach I to GEB. The regularities involved with water molecules are valid for both (I and II) Approaches to GEB.
Equations and equalities
Among the concentration balances one can distinguish equations and equalities. An equality, represented by the balance (11a), involves only one species (here: Na+1), whereas an equation for concentration balance involves more species, see Equations 10a or 17a. In the equality (11a), the value for [Na+1] is a number for the pre-assumed C and V0 values, at given V-value; as such, it can enter immediately the related ChB, see Equation 7b. Then (11a) is not considered as equation, when the number of equations be compared with the number of independent variables.
Number of independent equations and dependency/ independency property
In the system S1, three equations: {7b, 10a, 13a} form a set of three independent equations. In this context, four equations: {7b, 10a, 13a, 14a} or {7a, 10a, 13a, 22a}, and the more the five equations: {7a, 10a, 13a, 14a, 22a} form a set of linearly dependent equations in the System S1; in other words, the set of equations: {7a, 10a, 13a} or {7a, 10a, 14a} or {7a, 10a, 22a} can be chosen, optionally, as the set of equations involved in the algorithm applied for calculation purposes, see the computer program below, where Eq. 14a is involved.
Completeness of equilibrium constants
The first step in the formulation of redox systems according to GATES/GEB principles is gathering of the corresponding equilibrium data, i.e., the standard potentials E0j, and other equilibrium constants [1]. The set of equilibrium constants should be complete, as far as possible. The point is that these sets of data, often presented in the corresponding tables of equilibrium constants, are usually incomplete and/or refer to different equations of the related reactions. The related equilibrium constants can be obtained from other equilibrium constants, as will be shown below. Often, the tables of equilibrium constants contained in some studies are characterized by redundancy, i.e., the seemingly excessive number of physicochemical data, collected from various thematic studies, from different source works. Equilibrium constants values are subjected to errors – which means that even the results of tests performed under identical conditions may differ, in principle. The equilibrium constants are determined experimentally, by appropriate physicochemical methods. These equilibrium constants are parameters in the appropriate mathematical models, resolved with use of computer programs.
Relations between concentrations of the species; number of independent variables
From the interrelations obtained on the basis of complete set of independent expressions for equilibrium data chosen from ones collected in Table 1 (column D) [15], we have [8,10]:
| No | Reaction | Equilibrium relation | A [16] | B [17] | C [18] | D [15] |
|---|---|---|---|---|---|---|
| 1 | 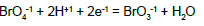 |
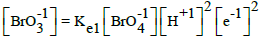 |
E01A = 1.745 | |||
| 2 | 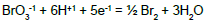 |
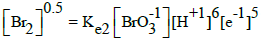 |
E02B = 1.482 | E02D = 1.52 | ||
| 3 | 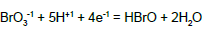 |
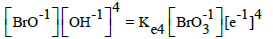 |
E03D = 1.45 | |||
| 4 | 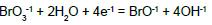 |
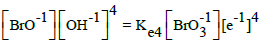 |
E04C = 0.54 | E04D = 0.54 | ||
| 5 | 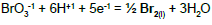 |
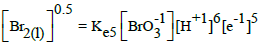 |
E05A = 1.513 | |||
| 6 | 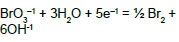 |
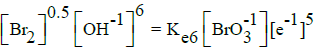 |
E06D = 0.50 | |||
| 7 | 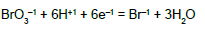 |
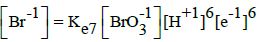 |
E07B = 1.423 | E07D = 1.45 | ||
| 8 | 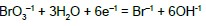 |
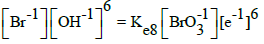 |
E08A = 0.613 | E08B = 0.61 | E08C = 0.61 | E08D = 0.61 |
| 9 | 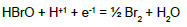 |
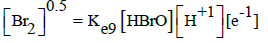 |
E09B = 1.574 | E09D = 1.6 | ||
| 10 | 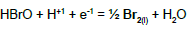 |
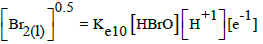 |
E010A = 1.584 | E010B = 1.596 | ||
| 11 | 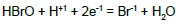 |
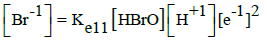 |
E011B = 1.331 | E011D = 1.34 | ||
| 12 | 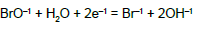 |
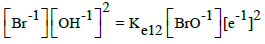 |
E012A = 0.766 | E012B = 0.761 | E012D = 0.76 | |
| 13 | 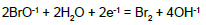 |
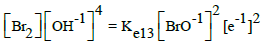 |
E013C = 0.45 | E013D = 0.45 | ||
| 14 | 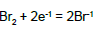 |
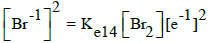 |
E014A = 1.098 | E014B= 1.0873 | E014C = 1.087 | E014D = 1.087 |
| 15 | 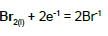 |
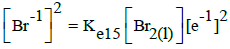 |
E015A = 1.078 | E015B = 1.066 | E015C = 1.065 | |
| 16 | 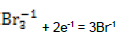 |
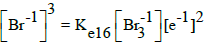 |
E016A = 1.062 | E016C = 1.05 | E016D = 1.05 | |
| 17 | 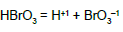 |
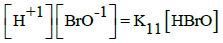 |
pK51C = 0.7 | |||
| 18 | 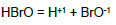 |
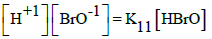 |
pK11C = 8.6 | pK11D = 8.7 | ||
| 19 | 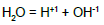 |
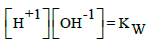 |
pKWC = 14.0 | pKWD = 14.0 |
Table 1: Equilibrium data related to different bromine species taken from the references indicated in columns A-D; the standard potentials (E0) values are expressed in SHE scale.
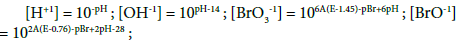
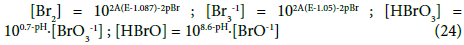
where the uniformly defined, three scalar variables: E, pH and pBr, forming a vector x = (x(1), x(2), x(3)) = (E, pH, pBr)T, are involved, where:
A∙E = –log[e-1], pH = –log[H+1], pBr = –log[Br-1] (25)
Three independent variables: xT = (E, pH, pBr) are involved in the systems S1 and S2 where, informally, E is ascribed to GEB (Equations 13a, 14a, or 22a), pH to ChB (Equation 7b), and pBr to the concentration balance for Br (Equation 10a).
The interrelations (24) were obtained on the basis of selected values for the corresponding, independent equilibrium constants presented in Table 1. All the variables in (24) are in the exponents of the power for 10 in: [e-1] = 10-A∙E, [H+1] = 10-pH, [Br-1] = 10-pBr, where 1/A = RT/F∙ln10; A = 16.9 at T = 298 K. The number of the (independent, ‘homogeneous’) variables equals to the number of equations, 3 = 3; this ensures a unique solution of the equations related to the systems S1 and S2, at the preset C0, C and V0 values, and the V-value at which the calculations are realized, at defined step of the calculation procedure, according to the computer program presented below. The E0j values were taken from references [15-18].
In Table 1 (numbers 5,10,15) we have also the data involved with liquid bromine, Br2(l). Solubility of Br2(l) is 35 g/L (20 °C) [19], i.e. s = 0.22 mol/L > C0 = 10-2 mol/L, and then [Br2(l)] = 0 in the systems S1, S2. HBrO4 is considered as unstable species [20,21].
Compatibility of the equilibrium constants
On the basis of E02B = 1.482 V (Table 1) and KW, we can calculate Ke6 and E06 for reaction BrO3-1 + 3H2O + 5e-1 = ½ Br2 + 6OH-1. From Ke2 and [Br-1]0.5[OH-1]6 = Ke6[BrO3-1][e-1]5 we have, by turns: Ke6 = Ke2(KW)6 → logKe6 = logKe2 – 6pKW → 5AE06 = 5AE02B – 6pKW; the value E06 = 1.482 – 6∙14/(5∙16.9) = 0.4879 ≠ E06D = 0.50 V in Table 1.
On the basis of E017 = 0.68 V for BrO4-1/Br-1 pair at pH = 14 [22] and KW, we calculate Ke and then E0 for BrO4-1 + 8H+1 + 8e-1 = Br-1 + 4H2O. For BrO4-1 + 4H2O + 8e-1 = Br-1 + 8OH-1 we have [Br-1][OH-1]8 = Ke17[BrO4-1][e-1]8; then Ke = Ke17/(KW)8 → logKe = logKe17 + 8pKW → 8AE0 = 8AE017 + 8pKW → E0 = 0.68 + 14/16.9 = 1.5084 V.
On the basis of E01A and E07B (Table 1) we calculate Ke and E0 for the reaction BrO4-1 + 8H+1 + 8e-1 = Br-1 + 4H2O we get E0 = 0.25∙1.745 + 0.75∙1.423 = 1.5035 ≠ 1.5084 V.
On the basis of Table 1 we obtain, by turns: (Ke7)2/(Ke5)2 = Ke14 → 2logKe7 – 2logKe5 = logKe14 → 2logKe7 = 2logKe5 + logKe14 → 2∙6AE07 = 2∙5AE05A + 2∙AE014B → E0 = E07 = (5E05A + E014B)/6 = (5∙1.513 + 1.098)/6 = 1.4438 V ≠ E07B, E07D.
In the links we do not find the pK11 values for HBrO = H+1 + BrO-1, K11 = [H+1][BrO-1]/[HBrO]. However, we can find it on the basis of relations:
(a) pK11 = logKe12 – logKe11 + 2∙pKW; e.g. (a1) pK11 = 2∙16.9∙(E012B – E011B) + 2∙14 = 8.734; (a2) pK11 = 2∙16.9∙(E012A – E011B) + 2∙14 = 8.903; (a3) pK11 = 2∙16.9∙(E012D – E011B) + 2∙14 = 8.700;
(b) pK11 = logKe12 – 0.5∙logKe14 – logKe9 + 2pKW; e.g., (b1) pK11 = 16.9∙(2∙E012A – E014A – E09B) + 2∙14 = 8.734; (b2) pK11 = 16.9∙(2∙E012B – E014C – E09B) + 2∙14 = 8.751; (b3) pK11 = 16.9∙(2∙E012D – E014B – E09B) + 2∙14 = 8.712; etc. The K11 values calculated on the basis of E0k values are not far distant from the pK11 values: 8.6 and 8.7 cited elsewhere (Table 1).
In conclusion, the relevant data found that do not differ dramatically among themselves [15-18].
It should be added that the data in columns A,B in Table 1 refer only to E0k. In addition, these equilibrium constants do not relate to the same stoichiometric reactions. However, based on the E0k values for the corresponding redox reactions one can obtain the values of other constants, e.g. concerning dissociation constants of the acid (here: HBrO).
A redundancy of the relevant data can also be noted – which means that some of the equilibrium constants from the given literature source can be obtained from other constants contained in that source. For example, from numbers 4, 6 and 13 in Table 1 we get Ke13D = (Ke6D)2/(Ke4D)2 → logKe13D = 2logKe6D – logKe4D → 2AE013D = 2∙5AE06D – 2∙4AE04D → E013D = 5E06D – 4E04D = 5∙0.5 – 4∙0.54 = 0.34 ≠ 0.45; the difference is greater, in this case. Note that E04D, E06D and E013D were not involved in the set of relations (24) and in the computer program presented below.
Even a small mismatch error resulting, for example, from the rounding of numerical values of the corresponding data, may cause a contradiction of the appropriate equations, where such constants are included within the same algorithm. Therefore, of primary importance is the selection of equilibrium constants that are independent to each other [23].
Computer program for the NaOH → Br2 system
function F = NaOH_Br2(x)
global V C0 V0C yy
E = x(1);
pH = x(2);
pBr = x(3);
H = 10^(-pH);
Kw = 10^-14;
pKw = 14;
OH = Kw/H;
A = 16.9;
Br = 10^-pBr;
ZBr = 35;
Br2=Br^2*10^(2*A*(E-1.087));
Br3=Br^3*10^(2*A*(E-1.05));
BrO=Br*10^(2*A*(E-0.76)+2*pH-2*pKw);
BrO3=Br*10^(6*A*(E-1.45)+6*pH);
HBrO = 10^8.6*H*BrO;
HBrO3=10^0.7*H*BrO3;
Na=C*V/(V0+V);
F = [%Charge balance
(H-OH+Na-Br-Br3-BrO-BrO3);
%Concentration balance for Br
(Br+3*Br3+2*Br2+HBrO+BrO+HBrO3+BrO3-2*C0*V0/(V0+V));
%Electron balance
((ZBr+1)*Br+(3*ZBr+1)*Br3+2*ZBr*Br2+(ZBr-1)*(HBrO+BrO)...
+(ZBr-5)*(HBrO3+BrO3)-2*ZBr*C0*V0/(V0+V))];
yy(1)=log10(Br);
yy(2)=log10(Br3);
yy(3)=log10(Br2);
yy(4)=log10(HBrO);
yy(5)=log10(BrO);
yy(6)=log10(HBrO3);
yy(7)=log10(BrO3);
yy(8)=log10(Na);
end
The volume V of the titrant (T) added is considered as a parameter, not variable; the V value is changed, in steps, in the calculation procedure, realized according to iterative computer program, here: MATLAB [1].
Final Comments
Calculations and graphical presentation of results
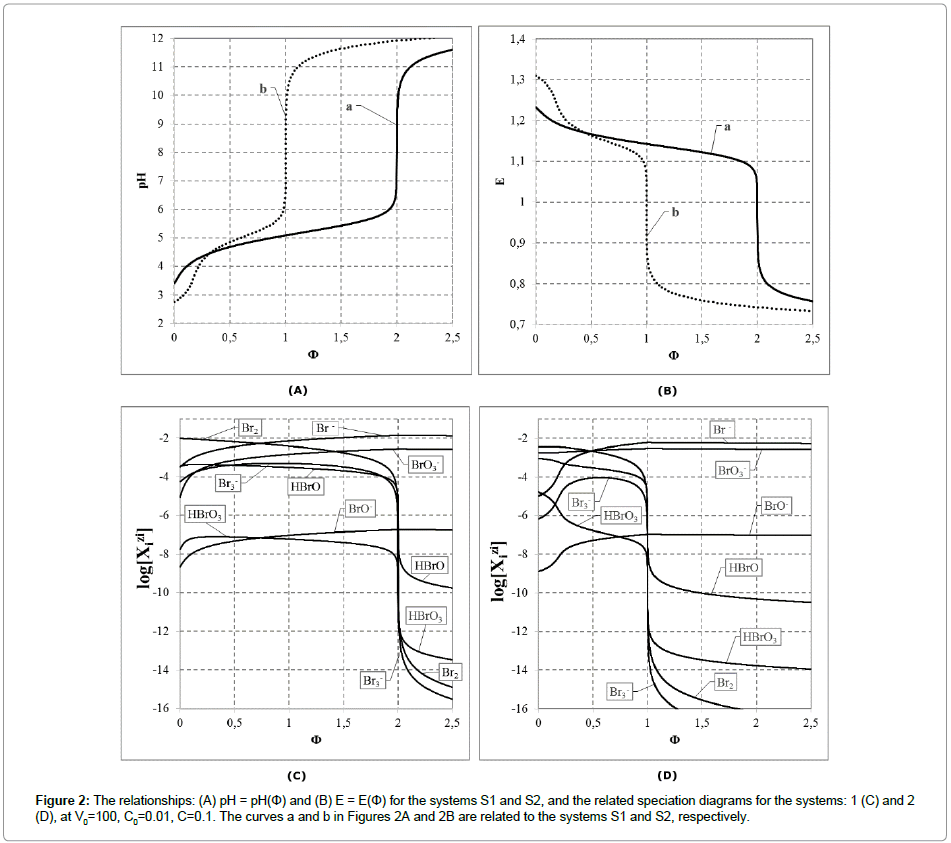
The calculation procedure, realized according to an iterative computer program, e.g. MATLAB, gives the set of points (Φ, pH, E). The data thus obtained can be presented numerically or graphically. Some results obtained for the system S1 are presented in Table 1. The titration curves: E = E(Φ) and pH = pH(Φ) for the systems S1 and S2 are presented in Figure 2 together with speciation diagrams, where the curves  were plotted for different bromine species (Table 2).
were plotted for different bromine species (Table 2).
| System S1 | System S2 | ||||
|---|---|---|---|---|---|
| NaOH → Br2 | NaOH → HBrO | ||||
| Φ | pH | E | Φ | pH | E |
| 1,995 | 6,666 | 1,0491 | 0,995 | 6,347 | 1,0720 |
| 1,996 | 6,728 | 1,0455 | 0,996 | 6,411 | 1,0681 |
| 1,997 | 6,811 | 1,0406 | 0,997 | 6,498 | 1,0630 |
| 1,998 | 6,933 | 1,0334 | 0,998 | 6,625 | 1,0555 |
| 1,999 | 7,161 | 1,0199 | 0,999 | 6,866 | 1,0412 |
| 2,000 | 8,143 | 0,9619 | 1,000 | 8,102 | 0,9682 |
| 2,001 | 8,966 | 0,9132 | 1,001 | 9,002 | 0,9150 |
| 2,002 | 9,244 | 0,8968 | 1,002 | 9,281 | 0,8985 |
| 2,003 | 9,413 | 0,8868 | 1,003 | 9,450 | 0,8885 |
| 2,004 | 9,534 | 0,8797 | 1,004 | 9,571 | 0,8814 |
| 2,005 | 9,628 | 0,8741 | 1,005 | 9,666 | 0,8758 |
Table 2: The sets of (Φ, pH, E) values taken from the vicinity of the equivalence points for the systems S1 and S2, at V0=100, C0=0.01, C=0.1.
Before 2006, the basic property of the balance 2∙f(O) – f(H) for redox systems was unknown at all in the scientific world, and the linear independency/dependency of 2∙f(O) – f(H) as the fundamental/ practical criterion distinguishing redox/non-redox systems of any degree of complexity was also unknown. The principles of GEB formulation were unknown in earlier literature. Here is the hidden simplicity, which had to be discovered by MichaÅ‚owski, as the Approach II to GEB. The discovery of the Approach II GEB would most likely be impossible without the prior discovery (1992) of the Approach I to GEB by MichaÅ‚owski.
The generalized electron balance (GEB) concept, valid for redox electrolytic systems, is considered as the law of Nature [3,8,10] related to electrolytic redox systems. The computer software applied to redox systems, denoted as GATES/GEB, is the emanation of balances for H and O, referred to aqueous media. The GEB is compatible with other (charge and concentration) balances and enables to resolve the electrolytic (mono- or/and two-phase) redox systems of any degree of complexity, within the scope of generalized approach to electrolytic systems (GATES), perceived as the thermodynamic approach to equilibrium and metastable systems, where all necessary physicochemical knowledge on the systems tested is involved. The advantages of GATES are illustrated on examples of redox and nonredox analytical systems. The GATES is perceived as the unrivalled tool applicable, among others: (a) to mathematical modelling of thermodynamic behavior of the systems, (b) in choice of optimal a priori conditions of chemical analyses, and (c) in gaining chemical information invisible in real experiments, in general. Furthermore, GATES is the basis for generalized equivalence mass (GEM) concept [24], considered as the advantageous alternative against the obligatory equivalence mass/“weight” concept, still suggested by IUPAC. According to GATES, any chemical reaction notation is only a basis to formulate the related expression for equilibrium constant according to mass action law.
GATES/GEB allows to track not only the individual titrations, but also the processes composed of several steps, as shown in the example of copper iodometric determination [9]; the entire analytical process is partitioned here into 4 stages: two preparatory stages, with non-redox reactions, and two further stages in which redox reactions occurred. The majority of the dynamic systems, realized according to titrimetric mode, is perceived also as an important tool in the classical chemical analysis.
The Approach II to GEB does not require any prior knowledge of the oxidation numbers of elements in the components and in the species; it is a fact of capital importance, particularly in relation to organic species (molecules, ions, radicals and ion-radicals), of any degree of complexity. Note that the ‘oxidation number’ was essentially the contractual concept [25-27]. If the oxidation numbers are easily determined, the Approach I to GEB, known as the ‘short’ version of GEB, can be applied. Within the Approaches I and II to GEB, the roles/terms of oxidants and reductants are not assigned a priori to individual components; GATES/GEB provides full ‘democracy’ in this regard.
For all redox systems, any linear combination of f12 = 2∙f(O) – f(H) with charge balance f0 = ChB and other elemental/core balances fk = f(Yk) (k=3,…,K) related to a redox system of any degree of complexity does not give the identity, 0 = 0, see e.g. [23]. The f12 is linearly dependent on f0,f3,…,fK when related to non-redox systems. In other words, the set of K independent balances f0,f12, f3,…,fK is applied for a redox system, or a set of K–1 balances f0,f3,…,fK is applied to a nonredox system with K–2 independent elemental/core balances fk = f(Yk) for Yk ≠ H, O. The independency or dependency property of f12 is then the general criterion distinguishing between redox and nonredox systems [4,11,23] of any degree of complexity, also in mixed- solvent media [28-30].
The difference between redox and non-redox systems is then ‘coded’ in f12. This unique, general property explains clearly why the elemental balances: f1 and f2 are not formulated for non-redox systems, of any degree of complexity. The f12 and any linear combination of f12 with f0,f3,…,fK for a given system retain full properties of the GEB. In other words, f12 is fully compatible with other (f0,f3,…,fK) balances and enables to resolve any electrolytic (mono- or/and two-phase) redox system within GATES, and GATES/GEB in particular.
All the inferences made within GATES/GEB are based on firmly established physical, physicochemical and algebraic foundations. Consequently, it allows to understand far better the physicochemical phenomena occurring in the system in question, and improve some methods of analysis. All the facts testify very well about the potency of simulated calculations made, according to GATES, on the basis of all attainable and preselected physicochemical knowledge involved.
Contrary to appearances, established by the current paradigm, the criterion distinguishing non-redox and redox systems is not immediately associated with free electrons in the related system; it provides a kind of uniformity in the formulas derived for this purpose. This fact, especially the simple calculations [9] of free electron concentrations in redox systems, deny the unique role of free electrons in elementary redox reactions, as described in half- or partial reactions, where the species of the same element with different oxidation numbers are involved. On the other hand, it points to the unique role of H and O in redox systems, suggested in earlier theoretical/hypothetical/qualitative considerations on these systems. Let’s repeat: the GEB concept, valid for redox electrolytic systems, is the emanation of balances for H and O, referred to aqueous media.
References
- Michałowski T (2011) Application of GATES and MATLAB for resolution of equilibrium, metastable and non-equilibrium electrolytic systems, In: Applications of MATLAB in science and engineering. Michałowski T (edt) InTech, Rijeka, Croatia, 1-34.
- Michałowski T (2010) The generalized approach to electrolytic systems: I. Physicochemical and analytical implications. Crit Rev Anal Chem 40: 2-16.
- Michałowski T, Toporek M, Michałowska-Kaczmarczyk AM, Asuero AG (2013) New trends in studies on electrolytic redox systems. Electrochimica Acta 109: 519-531.
- Michałowski T, Michałowska-Kaczmarczyk AM, Toporek M (2013) Formulation of general criterion distinguishing between non-redox and redox systems. Electrochimica Acta 112: 199-211.
- Michałowska-Kaczmarczyk AM, Toporek M, Michałowski T (2015) Speciation diagrams in dynamic Iodide + Dichromate system. Electrochimica Acta 155: 217-227.
- Toporek M, Michałowska-Kaczmarczyk AM, Michałowski T (2015) Symproportionation versus disproportionation in bromine redox systems. Electrochimica Acta 171: 176-187.
- MichaÅ‚owska-Kaczmarczyk AM, Asuero AG, MichaÅ‚owski T (2015) “Why not stoichiometry” versus “Stoichiometry – why not?” Part I. General context. Crit Rev Anal Chem 45: 166-188.
- MichaÅ‚owska-Kaczmarczyk AM, Asuero AG , Toporek M, MichaÅ‚owski T (2015) “Why not stoichiometry” versus “Stoichiometry – why not?” Part II. GATES in context with redox systems. Crit Rev Anal Chem 45: 240-268.
- MichaÅ‚owska-Kaczmarczyk AM, MichaÅ‚owski T, Toporek M, Asuero AG (2015) Why not stoichiometry” versus “Stoichiometry – why not?” Part III, Extension of GATES/GEB on complex dynamic redox systems. Crit Rev Anal Chem 45: 348-366.
- MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A, MichaÅ‚owski T (2017) Generalized electron balance (GEB) as the law of nature in electrolytic redox systems, In: Redox: principles and advanced applications, MA Ali Khalid (edt), InTech, Rijeka, Croatia, 10-55.
- MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A , MichaÅ‚owski T (2017) A distinguishing feature of the balance 2∙f(O) – f(H) in electrolytic systems. The reference to titrimetric methods of analysis, In: Advances in titration techniques, Vu Dang Hoang (edt), InTech, Rijeka, Croatia, 174-207.
- MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A , MichaÅ‚owski T (2017) Principles of titrimetric analyses according to GATES, In: Advances in titration techniques Vu Dang Hoang (Edt), InTech, Rijeka, Croatia, 133-171.
- MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A , MichaÅ‚owski T (2017) Some remarks on solubility products and solubility concepts, In: Descriptive inorganic chemistry. Researches of metal compounds T Akitsu (edt), InTech, Rijeka, Croatia, 93-134.
- Marx D, Tuckerman ME, Hutter J, Parrinello M (1999) The nature of the hydrated excess proton in water. Nature 397: 601-604.
- Lurie Yu (1971) Handbook of Analytical Chemistry, Mir Publishers, Moscow.
- Daniel CH (2007) Quantitative chemical analysis, (7th edtn)WH Freeman and Company, USA.
- Vanysek P (2010) CRC Handbook of Chemistry and Physics, (91st edtn), CRC Press, Florida, United States.
- Nikolsky BP (1964) Guide for Chemists: Chemical equilibrium and kinetics, In: Properties of solutions, Electrode Processes (3rdedtn), Publishing House, Moscow.
- Properties of Methoxyacetone.
- Pauling L (1988) General Chemistry, Dover Publications, USA.
- Rastogi RP (2008) Introduction to non-equilibrium physical chemistry, In: Towards complexity and non-linear science, Amsterdam, Elsevier, 150.
- Perbromate anion.
- Michałowska-Kaczmarczyk AM, Michałowski T (2013) Comparative balancing of non-redox and redox electrolytic systems and its consequences. Am J Analyt Chem 4: 46-53.
- Michałowski T, A Pietrzyk, M Ponikvar-Svet, M Rymanowski (2010) The generalized approach to electrolytic systems: II. The generalized equivalent mass (GEM) concept. Crit Rev Anal Chem 40: 17-29.
- Karen P, McArdle P, Takats J (2016) Comprehensive definition of oxidation state (IUPAC Recommendations 2016). Pure Appl Chem 88: 831-839.
- Karen P (2015) Oxidation state, a long-standing issue! Angew Chem Int Ed Engl 54: 4716-4726.
- Karen P, McArdle P, Takats J (2014) Toward a comprehensive definition of oxidation state (IUPAC Technical Report). Pure Appl Chem 86: 1017-1081.
- Michałowski T, Pilarski B, Asuero AG , Michałowska-Kaczmarczyk AM (2014) Modeling of acid-base properties in binary-solvent systems In: Handbook of solvents. George Wypych (edt), (1stedn) ChemTec Publishing, Toronto, 623-648.
- Michałowska-Kaczmarczyk AM, Michałowski T (2014) Generalized electron balance for dynamic redox systems in mixed-solvent media. J Analyt Sci, Methods Instrumentation 4: 102-109.
- Michałowska-Kaczmarczyk AM, Michałowski T (2014) Linear dependence of balances for non-redox electrolytic systems. Am J Analyt Chem 5: 1285-1289.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi