Research Article, Res J Econ Vol: 2 Issue: 2
Healthcare Expenditure, Economic Growth, and Inflation in the G7 Countries: A Panel Cointegration Approach
Sima Siami-Namini*
Department of Agricultural and Applied Economics, Texas Tech University, USA
*Corresponding Author : Sima Siami-Namini, PhD
Student and Graduate Research Assistant, Department of Agricultural and Applied Economics, Texas Tech University, USA
E-mail: sima.siami-namini@ttu.edu
Received: January 16, 2018 Accepted: February 05, 2018 Published: February 12, 2018
Citation: Siami-Namini S (2018) Healthcare Expenditure, Economic Growth, and Inflation in the G7 Countries: A Panel Cointegration Approach. Res J Econ 2:2.
Abstract
The main aim of this research article is to explain the relationship between the healthcare expenditure, economic growth and inflation in a panel data of the G7 countries for the period 1995 to 2013 by using panel co-integration analysis. To explore the effect of inflation on healthcare expenditure, this article constructs two individual models using the consumer price index (CPI) inflation in the first, and the personal consumption expenditure price index (PCE) in the second. The CPI inflation has been used to calculate the change in the out-of-pocket expenditure of all urban households, while, the PCE inflation was used to measure spending on behalf of households. The results show that the CPI inflation has the most effect on healthcare expenditure rather than the PCE inflation. Also, healthcare expenditure is a necessary good as the short-run income elasticity is less than one for both two models. Using vector error correction model (VECM), the econometric results showed that there is a strong short-run Granger causality from economic growth and price index to healthcare expenditure in both models. Moreover, the impulse response function (IRF) analysis showed that there is a strong positive bidirectional long-run Granger causality between healthcare expenditure and economic growth, and a strong negative bidirectional long-run Granger causality between healthcare expenditure and inflation in both models.
Keywords: Healthcare expenditure; Economic growth; Consumer Price Index(CPI) inflation; The Personal Consumption Expenditure (PCE)inflation; Panel cointegration; The G7 countries
Introduction
In analyzing of the healthcare expenditure in the countries, most studies have found a strong positive relationship between healthcare expenditure and economic growth, and therefore the spillover effect is of much importance to the private and the public investors, as well as policymakers. Obviously, the healthcare sector provides a major source of employment for highly skilled workers in the areas of healthcare services, manufacture medical equipment or drugs, medical insurance which facilitate the provision of healthcare to patients. On the other hand, rising healthcare expenditure as a share of gross domestic product (GDP) has caused issues about the negative compounding impact of healthcare inflation (The healthcare costs will be one of the most significant expenses in retirement period) in both developed and developing countries over the last decades, and especially after the global financial crisis in 2007 and 2008. In the 1960s, the economist William Baumol noted that personalized services can fall into a stagnation trap characterized by rapidly increasing cost inflation. Therefore, healthcare inflation is far higher than the natural rate of inflation, creating high real costs which push up healthcare expenditure [1]. Consequently, increases in the healthcare expenditure can harm the economy by the reduction of real GDP and increasing inflation and unemployment [2]. According to the historical data from the World Bank, healthcare expenditure accounts for over 10 percent of GDP in the G7 countries during 1995- 2013. The total healthcare expenditure per capita rose at an average annual rate of 4.6 percent in the G7 countries between 1995 and 2013, while real GDP per capita grew 1.1 percent annually. Within the G7 countries, the United States with an average of ($6,370) has the highest amount of healthcare expenditure per capita, followed by Germany ($3,379), and Canada ($3,333). Table 1 represents several health-related indicators in the G7 countries over the period of 1995-2013.
| Country | Canada | France | Germany | Italy | Japan | U.K. | U.S. |
|---|---|---|---|---|---|---|---|
| GDP Per Capita, Growth (Annual %) | 1.4991 | 1.0526 | 1.3241 | 0.19905 | 0.7335 | 1.4865 | 1.4755 |
| Healthcare Expenditure Per Capita, PPP (Constant 2011 International $) | 3333 | 3167 | 3379 | 2434 | 2484 | 2458 | 6370 |
| Healthcare Expenditure, Total (% of GDP) | 9.68 | 10.80 | 10.76 | 8.36 | 8.29 | 7.94 | 15.00 |
| Healthcare Expenditure, Private (% of GDP) | 2.87 | 2.34 | 2.35 | 1.98 | 1.55 | 1.46 | 8.23 |
| Healthcare Expenditure, Public (% of GDP) | 6.81 | 8.46 | 8.41 | 6.38 | 6.74 | 6.49 | 6.78 |
| Healthcare Expenditure, Private (% of Total Health Expenditure) |
29.70 | 21.58 | 21.77 | 23.87 | 18.70 | 18.45 | 54.95 |
| Healthcare Expenditure, Public (% of Total Health Expenditure) |
70.30 | 78.42 | 78.23 | 76.13 | 81.30 | 81.55 | 45.05 |
| Population Ages 65 and Above (% of Total) | 13.20 | 16.34 | 18.31 | 19.11 | 19.48 | 16.17 | 12.68 |
| Life Expectancy at Birth, Total (Years) | 79.88 | 80.03 | 78.78 | 80.54 | 81.75 | 78.81 | 77.33 |
Table 1: Health-Related Indicators in the G7 Countries (1995-2013).
As shown in Table 1, the United States spends far more on healthcare expenditure than the others, and it cannot be attributed to higher income, aging, or utilization of hospitals and doctors or other factors. The evidence indicates that the higher expenditure is more likely due to higher prices and perhaps more readily accessible technology. Of the countries studied, Italy, U.K., and Japan have the lowest healthcare expenditure based on purchasing power parity (PPP), which they make through aggressive pricing regulations. The U.S. economy with 15 percent has the highest healthcare expenditure as a percentage of GDP. Total healthcare expenditure is the sum of the public and the private healthcare expenditure. In comparing with the other sectors of the economy, a large share of healthcare expenditure is funded by the public sector in the G7 countries except for the United States. The private healthcare expenditure in the U.S. as a share of GDP is the highest viewing figures between the G7 countries. Totally, the figures show that government supported as high as 73 percent of healthcare expenditure, and hence the share of private business and households reached to an average of 27 percent of the healthcare expenditure between 1995 and 2013 in the G7 countries. Occasionally, aging is a major issue within the G7 countries, because increases the demand for healthcare delivery, and hence raises the prices of healthcare services. In fact, with the population aging, investing in the healthcare industry have its upsides. Therefore, real GDP as a proxy of income is the main driver of healthcare expenditure, and then economic growth will be important for policymakers. Also, life expectancy has been one of the most common indicators of healthcare status in a country. As shown in Table 1, Japan with 81.75 years, and Italy with 80.54 years, and then France with 80.03 years, respectively, have the highest average life expectancies between the G7 countries for the sample of studies. Most of the literature to date has focused on analyzing the relationship between healthcare expenditure and economic growth, and yet a key question remains to explore the relationship between inflation and healthcare expenditure. Then my contribution to the current literature is to analyze the short- and the long-run relationship between the real per capita healthcare expenditure, real per capita GDP and inflation in the G7 countries including Canada, France, Germany, Italy, Japan, United Kingdom, and the United States from 1995 to 2013. Using panel data Granger causality based on a vector error correction model (VECM), which provides a more comprehensive test of causality than the standard Granger causality test, the article aims to know whether the relationship between the real per capita healthcare expenditure and economic growth and the relationship between the real per capita healthcare expenditure and inflation are still positive and negative, respectively. To do this, I use the consumer price index (CPI) inflation to measure price changes in goods and services purchased out of pocket by urban consumers, and the personal consumption expenditure (PCE) inflation to measure the changes in goods and services consumed by all households, and nonprofit institutions serving households, and estimate two individual models. The main reason is that some items and expenditures in the PCE inflation are outside the scope of the CPI inflation [3].
The rest of this article is structured as follows. The following section represents literature review. Then, I provide data and discuss the econometric methods adopted for the empirical analysis. In the next section, I explain the empirical estimation results in the several steps, first, check whether all variables are non-stationary, second test whether variables form a cointegrating set by using panel cointegration method, third if they are linked in the long-run, estimate the short-and the long-run income and price elasticity, and fourth explore the short- and the long-run Granger causality between variables. I present conclusions in the last section.
Literature Review
An emerging theoretical literature explores a two-way relationship between healthcare expenditure and economic growth. Healthcare expenditure is a function of income or resources available both in the private and the public sectors. On the other hand, healthcare spending in health insurance, investment in equipment, and government programs can stimulate the economy through enhancing the productivity of human capital. Because health is known as a determinant of human capital, and labor productivity, so, rises in healthcare expenditure will increase labor supply and productivity, and then lead to a higher income. A growing body of research studies indicates that variation in healthcare expenditure per capita could be explained by variations in GDP per capita. I am convinced that healthy people can increase more income because of their relatively high productivity, and the factors like higher education can cause better health and made more income [4-6]. The findings of some related studies explain that a half of differentials in economic growth between developed and developing countries are attributed to healthcare expenditure, and show a positive correlation between healthcare expenditure and economic growth [7]. The early history of empirical literature has focused on the factors influencing healthcare expenditure, but they tended to investigate the relationship between healthcare expenditure and economic growth [8-21]. Hartwig et al. [22] examined the Baumol’s model of ‘unbalanced growth’ for analyzing the healthcare expenditure by using pooled cross-section and time series data of 19 OECD countries. He used the difference between wage and productivity growth as the Baumol’s variable which is found to contribute significantly to the explanation of healthcare expenditure. Baumol et al. [23] describes nominal wage growth in excess of productivity growth as the main determinant of the rise in healthcare expenditure.
The other side of the debate is whether the income elasticity of healthcare expenditure is greater or less than one which is classified as a ‘luxury’ or a ‘necessary’, respectively [24]. For instance, Feldstein et al. [25] explained that while families with higher incomes have greater expenditure on medical care, the percentage of income spent on medical care declines as income increases. Gerdtham et al. [26] used a panel data of 20 OECD countries over the period of 1960 through 1987 and estimated a regression for healthcare spending as a function of GDP and several other variables, including institutional and socio-demographic factors, and found that income elasticity is greater than one, and then concluded that healthcare expenditure is a ‘luxury’ good. In time series analysis, Erdil et al. [27] investigated the Granger-causality relationship between real per capita GDP and real per capita healthcare expenditure by using a panel data set of different income groups of countries with a vector auto-regression (VAR) representation. The findings showed the existence of one-way causality runs from income to healthcare in low- and middle-income countries since the reverse holds for high-income countries. Baltagi et al. [28] investigated the long-run relationship between healthcare expenditure and GDP by using a panel data of 20 OECD countries for the period 1971-2004 and found that healthcare expenditure is a necessity good and not a luxury good, with income elasticity less than previous studies. Freeman et al. [29] estimated the income elasticity of healthcare expenditure by using annual data on healthcare spending in the U.S. states for the period of 1966-2009. The results of the first difference models presented consistent estimates across time periods, whether expressed as averages of individual state estimates or pooled time series. Income elasticity for the full sample falls in the range 0.21-0.22, which was lower than earlier studies. Magazzino et al. [30] examined the healthcare expenditure in Italian regions, by applying the model selection procedure and panel data approach to find the determinants of healthcare expenditure at the state level. The findings suggested that the real gross state product (GSP), the unemployment rate, the number of beds in community hospitals, the urbanization degree and the percentage of the population with at least the junior high school degree had a direct impact on the real healthcare outlay. Also, the income elasticity was equal to 0.83-0.88 for the static panel estimates, and 0.43-0.48 for the dynamic methods, implying that health expenditure is a necessity good and not a luxury good at the state level.
Data
In this article, I use annual data of the G7 countries from 1995 to 2013, gathered from the Organization for Economic Cooperation and Development (OECD) Health Statistics in different years, and World Development Indicators (WDI) of the World Bank. The main reason for selecting the Group of Seven (G7) in this article is that they spent a higher portion of their GDP on healthcare than the average of OECD countries. I collected information on healthcare expenditure per capita based on Purchasing Power Parity [PPP] (HCE) (Constant 2011 international $), GDP per capita based on PPP (Constant 2011 international $), the consumer price index (CPI) (2011=100), the personal consumption expenditure (PCE) price index (2011=100), population ages 65 and above (POP65) (% of total), and life expectancy at birth (LE), total (years). All variables are expressed in natural logarithm. Table 2 represents the descriptive statistics of the variables.
| Variables | Mean | Std. Dev. | Min | Max | Skewness | Kurtosis | Jarque-Bera |
|---|---|---|---|---|---|---|---|
| HCE | 8.0323 | 0.4160 | 7.2057 | 9.1211 | 0.5022 | 3.1121 | 5.6603 |
| GDP | 10.5226 | 0.1291 | 10.2512 | 10.8462 | 0.7329 | 3.2602 | 12.2831 |
| PCE | 4.3622 | 0.2047 | 3.9368 | 4.7057 | -0.4523 | 2.1470 | 8.5671 |
| CPI | 4.4858 | 0.1181 | 4.2156 | 4.6583 | -0.3156 | 1.8919 | 9.0119 |
| LE | 4.3766 | 0.0227 | 4.3257 | 4.4228 | -0.0610 | 2.1209 | 4.3653 |
| POP65 | 2.7852 | 0.1807 | 2.4798 | 3.2219 | 0.0898 | 2.2704 | 3.1288 |
Table 2: Descriptive Statistics.
Table 3 represents the correlation statistics between variables. Although there is no perfect collinearity between variables, there is a high positive correlation between HCE (as a dependent variable) and GDP (as an independent variable) about 92.5 percent. The best regression models are those in which the independent variables, each correlate highly with the dependent variables, but correlate at most only minimally with each other. Also, HCE has a high positive correlation with the PCE inflation (about 56.6 percent) than the CPI inflation (about 36.3 percent). Correspondingly, HCE has low positive and low negative correlation with LE and POP65, respectively.
| Variables | HCE | GDP | PCE | CPI | LE | POP65 |
|---|---|---|---|---|---|---|
| HCE | 1 | |||||
| GDP | 0.9250 | 1 | ||||
| PCE | 0.5655 | 0.3957 | 1 | |||
| CPI | 0.3632 | 0.1688 | 0.6521 | 1 | ||
| LE | 0.0102 | - 0.1692 | 0.3603 | 0.7893 | 1 | |
| POP65 | - 0.2392 | - 0.3724 | 0.2535 | 0.4720 | 0.6698 | 1 |
Table 3: Correlation Statistics.
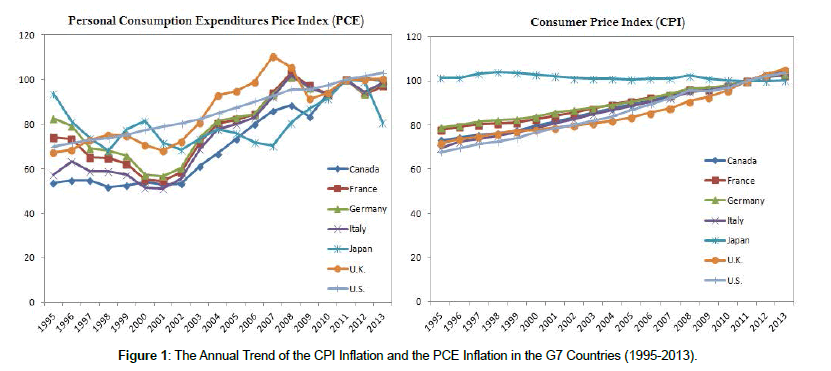
As I mentioned before, there is the conceptual differences between the CPI inflation and the PCE inflation as “scope effects”. The CPI inflation is used to calculate the change in the out-of-pocket expenditure of all urban households. While, the PCE inflation is used to measure the changes in goods and services consumed by all households, and non-profit institutions serving households in the National Income and Product Accounts (NIPA). It means that some items of expenditure in the PCE inflation are outside the scope of the CPI inflation. In addition to households’ spending, the PCE inflation measures spending on behalf of households. The PCE inflation also considers estimated spending on some goods and services that do not have market prices, such as free financial services and employerfunded medical care and insurance programs [3]. Figure 1 shows the annual trend of the CPI inflation and the PCE inflation between the G7 countries during the period of 1995 to 2015. As shown in Figure 1, the PCE inflation for all the G7 countries (with the exception of the United States) have larger fluctuations than the CPI inflation. So, to explore the effect of the CPI inflation and the PCE inflation on the healthcare expenditure in the G7 countries, I build two individual models.
Methods
The overall theory of the endogenous growth models debates the mechanism which the healthcare expenditure affects economic growth. Neo-classical growth models explain economic growth based on savings and growth of population. Solow et al. [31] highlighted that countries with higher savings will have higher per capita income by the assumption of ceteris paribus. In Solow’s model, the rate of savings and population are the principal determinants of per capita income between countries. Buchanan et al. [32] developed a theoretical model, encouraging public authorities to increase public spending on health independent of demand. This theory highlights that inefficiency in the provision of healthcare should be observed not only by lack of supply of healthcare services but also by reducing quality such as congestion, infrastructure, and unequal distribution of staff [33].
Theoretically, several models were developed to join the impact of human capital on economic development. For example, Romer et al. [34] and Barro et al. [35] emphasized that human capital is a very important factor in boosting economic development. The augmented Solow model emphasized the importance of human capital on economic growth [36]. These endogenous models are based on the ability of human capital to influence economic growth in the short- and the long-run. The theoretical model developed in this article highlights a functional relationship between economic growth and healthcare expenditure which is one of the components of human capital.
On the other hand, the consumer demand theory states the consumer has the objective of maximizing satisfaction and hence income is allocated among competing goods and services based on their prices. Then, in this article, I consider two individual models using three proper variables in each including HCE, GDP and the CPI inflation in the model (I), and HCE, GDP, and the PCE inflation in the model (II).
To test the nature of the association between the variables while avoiding any spurious correlation, the empirical investigation in this article follows several steps. As a first step, I begin by testing for non-stationary of variables, including HCE, GDP, CPI, and PCE. Prompted by the existence of unit roots in the time series, I test for the long-run cointegrating relation between variables as a second step of estimation using the panel cointegration technique developed by Pedroni et al. [37]. Granted the long-run relationship, this study attempts to measure the short- and the long-run income and price elasticity using the method obtained from Roberts et al. [16] as a third step.
Assuming a first order heterogeneous, dynamic model for dependent variable with two explanatory variables
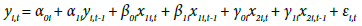 (1)
(1)
Where yi,t is dependent variable (here HCE), x1i,t is the first independent variable (here GDP), and x2i,t is the second independent variable (here CPI in the model (I) and PCE in the model (II)). The short-run elasticity of yi,t with respect to x1i,t and x2i,t are β0i and γ0i, respectively. The long-run elasticity of yi,t with respect to x1i,t and x2i,t is calculated by 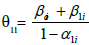 , and
, and 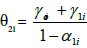 respectively.
respectively.
As a fourth step, a panel vector error correction model (VECM) is built to find the Granger-causality relation between variables as follows:
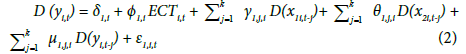
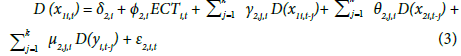
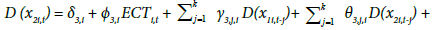
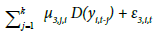 (4)
(4)
Where i refer to the country (i= 1,2,…,7), and t is time trend j is the best lag considering the Akaike information criterion (AIC). Also, ECTi,tis the error correction term derived from the long-run cointegrating relationship,Ï•1,i , Ï•2,i , Ï•3,iare adjustment coefficients and ε1,i,t , ε2,i,t and ε3,i,tare disturbance terms. I determine the sources of causation by testing for the significance of the coefficients of the lagged variables in equations (2) through (4). To do this, firstly, I explain the Granger short-run causality using F-statistic for testing the null hypothesis (H0 : γ1,j,i = 0,or θ1,j,i = 0) in equation (2), (H0 : θ2,j,i = 0,or μ2,j,i = 0) in equation (3), (H0 : γ3,j,i = 0,or μ3,j,i = 0) in equation (4), respectively. If the null hypothesis of no Granger causality is rejected, then the existence of Granger short-run causality is confirmed; secondly, I explore the Granger long-run causality using the ECT coefficients in the above equations. If the ECTs coefficients are zero (Ï•1,i = 0 or Ï•2,i = 0 or Ï•3,i = 0), then there is no Granger long-run causality from explanatory variable to the dependent variable; and thirdly, I can jointly check the existence of both Granger short- and long-run causalities using F-statistic by testing null Hypothesis (H0 : γ1,j,i = 0, or θ1,j,i = 0 or Ï•1,i = 0) in equation (2), (H0 : θ2,j,i = 0, or μ2,j,i = 0 or Ï•2,i = 0) in equation (3), and (H0 : γ3,j,i = 0, or μ3,j,i = 0 or Ï•3,i = 0) in equation (4). As the last step, I use the forecast error variance decomposition (FEVD) and the impulse response function (IRF) analyses to explain the dynamic interaction between healthcare expenditure, GDP and the CPI inflation in the model (I) and between healthcare expenditure, GDP and the PCE inflation in the model (II).
Empirical Results
Panel Unit Roots tests
In this section before proceedings begin, I test the unit root properties of the variables through pooling of the panel data for testing the unit root null hypothesis. Table 4 shows the results of the panel unit root tests. As shown in Table 4, the results of the panel unit root tests illustrate that a large most of panel unit root tests for each variable are non-stationary or integrated of order one in level, but they become stationary after first differencing of variables. In other words, the unit root null hypothesis at the 5% level of significance is not rejected for all variables. When one takes the first difference of each variable, all various estimation methods for panel unit root tests consistently reject the unit root null hypothesis at the 5% level of significance.
| Methods | HCE | GDP | CPI | PCE | ||||
|---|---|---|---|---|---|---|---|---|
| Level | First Difference | Level | First Difference | Level | First Difference | Level | First Difference | |
| H0 : Unit root | ||||||||
| Levin et al. [38] t* | -2.7471 (0.0030) | - (-) |
-4.5184 (0.0000) |
- (-) |
0.7990 (0.7879) |
-4.9188 (0.0000) |
-0.3131 (0.3771) |
-5.6047 (0.0000) |
| Breitung et al. [39] t-stat | 0.7076 | -1.6753 | 1.4289 | -4.6336 | -0.8265 | -3.2523 | -0.7945 | -1.8008 |
| (Intercept and Trend) | (0.7604) | (0.0469) | (0.9235) | (0.0000) | (0.2043) | (0.0060) | (0.2134) | (0.0359) |
| Im et al. [40] W-Stat | 0.9761 (0.8355) |
-2.0493 (0.0202) |
-1.1302 (0.1292) |
-2.9768 (0.0015) |
4.0557 (1.0000) |
-4.6799 (0.0000) |
1.1651 (0.8780) |
-3.7536 (0.0001) |
| ADF-Fisher Chi-Square | 12.0822 (0.5997) |
25.4903 (0.0300) |
20.1408 (0.1258) |
32.3881 (0.0035) |
2.6330 (0.9996) |
49.2523 (0.0000) |
8.2342 (0.8768) |
38.5312 (0.0004) |
| PP-Fisher Chi-Square | 8.53027 (0.8599) |
38.6452 (0.0004) |
27.9098 (0.0146) |
54.1611 (0.0000) |
13.1314 (0.5162) |
73.9559 (0.0000) |
5.2154 (0.9826) |
33.3637 (0.0026) |
| H0: Stationarity | ||||||||
| Hadri et al. [41] Z-Stat | 7.26076 (0.0000) |
- (-) |
6.37168 (0.0000) |
- (-) |
7.4702 (0.0000) |
- (-) |
5.56965 (0.0000) |
- (-) |
Table 4: The Results of Panel Unit Root Tests.
Panel Cointegration test
In this section, I explore the long-run relationship between variables through the panel cointegration tests. Table 5 presents the results of the panel cointegration tests for both models (I) and (II). As shown in Table 5, the null hypothesis of no cointegration for both models can be rejected based on the results of several methods. For example, three out of the eleven tests listed in Pedroni et al. [37-42] residual cointegration test (including four weighted statistics) reject the null hypothesis of no cointegration at the 5% significance level for both models. Subsequently, the Kao et al. [43] residual cointegration test rejects the null hypothesis of no cointegration at the 5% level of significance for both models (I) and (II). Finally, the Johansen Fisher-type test using an underlying Johansen method proposed by Maddala et al. [44] reaches to the same results by the likelihood ratio trace statistics and the largest Eigenvalue statistics equal to 31.03 in the model (I) and equal to 36.62 in the model (II), and find the presence of cointegration vectors in non-stationary time series. All Together, performed test statistics show that there is a cointegrating relationship between variables in both models by using panel data of the G7 countries.
| Methods | Statistic (Prob.) | |
|---|---|---|
| Model (Ι) | Model (ΙΙ) | |
| Pedroni Residual Cointegration Test | ||
| H0: No Cointegration HA: Common AR coefs. (within-dimension) |
||
| Panel v-Statistic | 0.5027 (0.3076) | 0.3363 (0.3683) |
| Panel rho-Statistic | 0.0437 (0.5174) | 0.3388 (0.6326) |
| Panel PP-Statistic | -0.7212 (0.2354) | -0.6285 (0.2649) |
| Panel ADF-Statistic | -0.9687 (0.1663) | -2.1776 (0.0147) |
| Panel v-Statistic (Weighted) | 1.8362 (0.0332) | 0.6331 (0.2633) |
| Panel rho-Statistic (Weighted) | -0.0721 (0.4713) | 0.3914 (0.6523) |
| Panel PP-Statistic (Weighted) | -0.9553 (0.1697) | -0.4351 (0.3317) |
| Panel ADF-Statistic (Weighted) | -2.5365 (0.0056) | -1.9172 (0.0276) |
| H0: No Cointegration HA: Individual AR coefs. (between-dimension) |
||
| Group rho-Statistic | 1.1255 (0.8698) | 1.6008 (0.9453) |
| Group PP-Statistic | -0.5399 (0.2946) | -0.5139 (0.3037) |
| Group ADF-Statistic | -3.4342 (0.0003) | -2.7886 (0.0026) |
| Kao Residual Cointegration Test | ||
| H0: No Co-integration | ||
| ADF | -1.8556 (0.0318) | -2.0582 (0.0198) |
| Johansen Fisher Panel Cointegration Test | ||
| Fisher Stat. (from Trace test) | ||
| None | 75.86 (0.0000) | 64.10 (0.0000) |
| At most 1 | 36.48 (0.0009) | 39.87 (0.0003) |
| At most 2 | 31.03 (0.0055) | 36.52 (0.0009) |
| Fisher Stat. (from max-Eigen test) | ||
| None | 54.83 (0.0000) | 37.83 (0.0006) |
| At most 1 | 28.43 (0.0125) | 27.20 (0.0181) |
| At most 2 | 31.03 (0.0055) | 36.52 (0.0009) |
Table 5: The Results of Panel Cointegration Test.
Income and Price Elasticity
Table 6 presents the short- and the long-run elasticity of healthcare expenditure against GDP and inflation. As shown in Table 6, although some test statistics are insignificant, the results show that healthcare expenditure seems to be a necessary good as the short-run income elasticity is less than one for both two pooled model estimates. It means that in the short-run, whenever the consumer’s income rises, demand for healthcare service rises, but the increase for a healthcare service is less than proportional to the rise in income, so the proportion of expenditure on healthcare service falls as income rises. The results of the short-run income elasticity confirm the previous findings [25]. But the long-run income elasticity for healthcare expenditure varies quite a bit over the two estimation approaches. The short-run income elasticity for healthcare expenditure is equal to 0.1989 in the model (I) and 0.2053 in the model (II). The long-run income elasticity of healthcare expenditure is equal to 3.5094 in the model (I) and 2.9446 in the model (II). It means that in the long-run, demand for healthcare service increases more than proportionally as consumer income rises. The results of the long-run income elasticity confirm the previous findings [26]. The results show the change in the consumer behavior in the short- and the long-run.
| Variables | Model (Ι) | Model (ΙΙ) |
|---|---|---|
| α0i | -1.7470 (0.0001) | -1.5979 (0.0001) |
| HCEi,t-1 | 0.9307(0.0000) | 0.9296 (0.0000) |
| GDP1i,t | 0.1989 (0.0558) | 0.2053 (0.0563) |
| GDP1i,t-1 | 0.0443 (0.6663) | 0.0020 (0.9854) |
| CPI2i,t | -0.9957 (0.0000) | - |
| CPI2i,t-1 | 0.9516 (0.0000) | - |
| PCE2i,t | - | -0.0150 (0.5973) |
| PCE2i,t-1 | - | 0.0208 (0.4685) |
| Short-run Income Elasticity | 0.1989 < 1 | 0.2053 < 1 |
| Long-run Income Elasticity | 3.5094 | 2.9446 |
| Short-run Price Elasticity | -0.9957 | -0.0150 |
| Long-run Price Elasticity | -0.6364 | 0.0824 |
Table 6: The Results of the Short- and the Long-run Income and Price Elasticities.
Consequently, the short- and the long-run price elasticity of healthcare expenditure is lower than 1 for both models. The shortrun price elasticity of healthcare expenditure is equal to -0.9957 in the model (I) and -0.0150 in the model (II). The long-run price elasticity for healthcare expenditure is equal to -0.6364 in the model (I) and 0.0824 in the model (II). It means that the price elasticity of demand for healthcare expenditure is relatively inelastic in the short- and the long-run, and show that the percentage change in quantity demanded is smaller than that in price. In both models, the regression coefficient of GDP and the price index is positive and negative, respectively, and this is consistent with the theory. The regression coefficient of the CPI inflation in the model (I) is significant, but the regression coefficient of the PCE inflation in the model (II) is not significant. As a result, the CPI inflation has the most effect on healthcare expenditure [45,46].
Panel Granger-causality tests
The results of F test for both short- and long-run Granger causality between healthcare expenditure, economic growth and price index in both models (I) and (II) are presented in Table 7. As shown in Table 7, the results show a strong short-run causality from economic growth and price index to healthcare expenditure in both models (I) and (II). It means that both economic growth and inflation strongly influence the healthcare expenditure in the shortrun. Also, there is a short-run causality from healthcare expenditure to the CPI inflation in the model (I). Yet, healthcare spending does not have any significant effects on GDP in the short-run and support the previous results. In addition, the coefficients of the F-statistic for ECT in both models are statistically significant for economic growth and price index equations. It means that it is equilibrium in the longrun despite short-run shocks. Therefore, there is a bilateral long-run causality between GDP and the CPI inflation in the model (I) and between GDP and the PCE inflation in the model (II). Furthermore, the joint test indicates that there is a bilateral strong causality between variables in both models. In other words, when a shock occurs in the system, the variables would make short-run adjustments to restore long-run equilibrium.
| Dependent Variable | Short-run | Long-run | Joint (Short-run/Long-run) | ||||
|---|---|---|---|---|---|---|---|
| Model (I) | HCE | GDP | CPI | ECT | HCE, ECT | GDP, ECT | CPI, ECT |
| HCE | 0.6877 (0.6025) | 5.2122 (0.0003) | 2.8155 (0.0303) | 0.1424 (0.7069) | 0.5604 (0.7300) | 8.1449 (0.0000) | 2.2760 (0.0542) |
| GDP | 0.3466 (0.8457) | 4.7876 (0.0016) | 13.2402 (0.0000) | 22.1449 (0.0000) | 4.8057 (0.0007) | 9.7080 (0.0000) | 13.3720 (0.0000) |
| CPI | 0.3473 (0.0112) | 4.2765 (0.0034) | 10.9499 (0.0000) | 12.4315 (0.0007) | 5.2755 (0.0003) | 6.6302 (0.0000) | 24.2747 (0.0000) |
| Model (II) | HCE | GDP | PCE | ECT | HCE, ECT | GDP, ECT | PCE, ECT |
| HCE | 1.6577 (0.1814) | 8.1756 (0.0001) | 3.4096 (0.0207) | 0.7599 (0.3856) | 1.6165 (0.1765) | 8.0580 (0.0000) | 2.6492 (0.0380) |
| GDP | 1.3495 (0.2631) | 2.2821 (0.0842) | 0.9307 (0.4291) | 8.4629 (0.0045) | 3.9089 (0.0056) | 3.7395 (0.0072) | 2.6754 (0.0366) |
| PCE | 0.9757 (0.4077) | 2.7972 (0.0444) | 7.4800 (0.0002) | 9.7321 (0.0024) | 2.8993 (0.0260) | 4.6232 (0.0019) | 8.3260 (0.0000) |
Table 7: The Results of Panel Causality Tests (F-Statistics).
The Results of Impulse Response Function (IRFs)
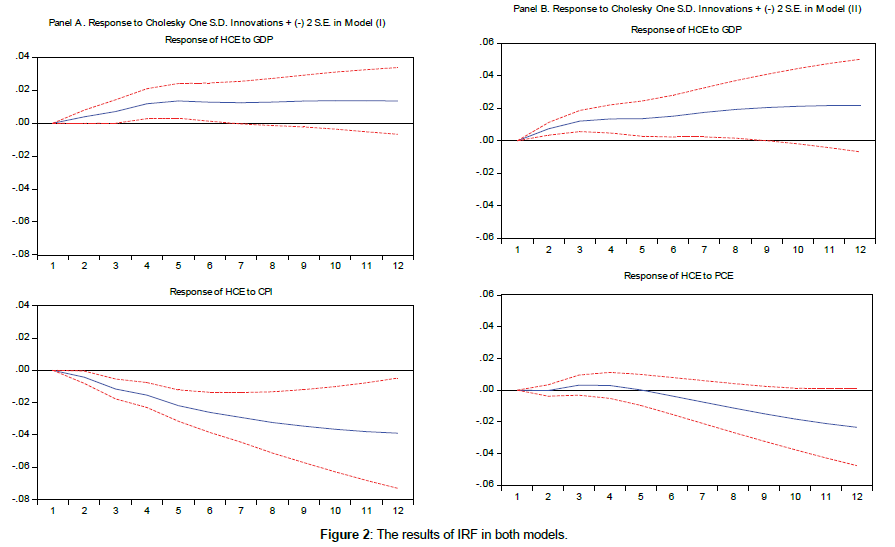
According to economic theory and the results of the impulse response function, there are complicated and significant relationships between variables in both two models. I undertook the forecast error variance decomposition (FEVD) and the impulse response function (IRF) analyses to explain the dynamic interaction between healthcare expenditure, economic growth and inflation in the G7 countries. In doing so, I give policymakers with more insight on the relative importance of random shocks and the response of variables to the shocks. In the long-run, all three variables are endogenous, thus they are causally related. The results of FEVD show that in the model (I), the CPI inflation is the most important variable in explaining shocks to healthcare expenditure (with 54.33 percent) than GDP (with 9.76 percent), while the CPI inflation and GDP, is the most important variable in explaining shocks to GDP (with 70.18 percent) and the CPI inflation (with 4.88 percent), respectively. In the model (II), income or GDP is the most important variable in explaining shocks to healthcare expenditure (with 20.84 percent) than the PCE inflation (with 11.16 percent), while the PCE inflation and GDP is the most important variable in explaining shocks to GDP (with 27.89 percent) and the PCE inflation (with 9.76 percent), respectively. In a similar vein, the IRF analysis in both models shows that shocks to healthcare spending have a positive impact on GDP; moreover, a shock to GDP also has a positive effect on healthcare expenditure in the G7 countries. The results implied that there is strong positive bidirectional Granger causality between healthcare expenditure and economic growth in the long-run. Consequently, the IRF show that shocks to healthcare spending have a negative impact on the CPI inflation and the PCE inflation. Moreover, a shock to the CPI inflation and the PCE inflation also has a negative effect on healthcare expenditure in the G7 countries. The results implied that there is strong negative bidirectional Granger causality between healthcare expenditure and the CPI inflation and between healthcare expenditure and the PCE inflation in the long-run. Figure 2 shows the IRF of healthcare expenditure to GDP and the CPI inflation in the model (I) (Panel A) and the IRF of healthcare expenditure to GDP and the PCE inflation in the model (II) (Panel B). As shown in Figure 2, when the impulse is the CPI inflation (in the Panel A), every response of healthcare expenditure is all negative at each time responsive period; but when the impulse is the PCE inflation (in the Panel B), there is a positive effect in the early period and then a negative effect for the rest of the period.
Conclusion
In this research article, I explored the relationship between healthcare expenditure, economic growth, and inflation in the G7 countries. Using a panel data of the G7 countries followed over 19 years, I have studied the non-stationarity and cointegration properties of the variables, ultimately measuring income and price elasticity of healthcare expenditure. The findings of a panel data unit root tests indicated that all variables are non-stationary in levels and become stationary after first differencing. The results of the panel cointegration test indicated that there is a cointegrating relationship between variables in the long-run. Therefore, I used a VECM approach to find the short- and the long-run Granger causality between variables. The result obtained was in line with the negative relationship economic theories explained and I concluded that inflation hampers healthcare expenditure, while economic growth increases it.
The results showed that healthcare expenditure is a necessary good as the short-run income elasticity is less than one for both two models. Also, the regression coefficient of GDP and price index is positive and negative, respectively, and the CPI inflation has the most effect on healthcare expenditure than the PCE inflation. The findings showed that there is a strong short-run causality from economic growth and price index to healthcare expenditure in both models. Also, there is short-run causality from healthcare expenditure to the CPI inflation in the model (I). The results showed that there is a bilateral long-run causality between GDP and the CPI inflation in the model (I) and a bilateral long-run causality between GDP and the PCE inflation in the model (II).
Moreover, the results of FEVD showed that in the model (I), the CPI inflation is the most important variable in explaining shocks to healthcare expenditure than GDP. In the model (II), GDP is the most important variable in explaining shocks to healthcare expenditure rather than the PCE inflation. The IRF analysis in both models showed that there is a strong positive bidirectional long-run Granger causality between healthcare expenditure and economic growth, and a strong negative bidirectional long-run Granger causality between healthcare expenditure and the CPI inflation and between healthcare expenditure and the PCE inflation.
References
- Erixon F, van der Marel E (2011) What is Driving the Rise in Healthcare Expenditure? An Inquiry into the Nature and Causes of the Cost Disease. ECIPE Working Article 05.
- Assistant Secretary for Planning and Evaluation (ASPE) (2005) Effects of Healthcare Spending on the U.S. Economy, USA.
- Index CP (2011) Bureau of Labor Statistics (BLS).
- Mushkin SJ (1962) Health as an Investment. J Polit Econ 70: 129-157.
- Gerdtham UG, Jönsson B (2000) International Comparisons of Health Expenditure: Theory, Data and Econometric Analysis, Amsterdam, UK.
- Muysken J, Yetkiner IH, Ziesemer T, (2003) Health, Labor Productivity and Growth, in Growth Theory and Growth Policy. London, UK.
- World Health Organization (2005) The World Health Report 2005, USA.
- Kleiman E (1974) The Determinants of National Outlay on Health. Macmillan, London, UK.
- Newhouse JP (1977) Medical Care Expenditure: A Cross-National Survey. J Hum Resour 12: 115-125.
- Parkin D, McGuire A, Yule B (1987) Aggregate Healthcare Expenditure and National Income. Is Healthcare a Luxury Good? J Health Econ 6: 109-127.
- Culyer AJ (1990) Healthcare Systems in Transition. Organization for Economic Cooperation and Development; Paris: Cost Containment in Europe in OECD: 29-40.
- Milne R, Molana H (1991) On the Effect of Relative Price on Demand for Healthcare: EC Evidence. App Econ 23: 1221-1226.
- Gerdtham UG, Jönsson B (1991) Conversion Factor Instability in International Comparisons of Healthcare Expenditure. J Health Econ 10: 227-234.
- Hitiris T, Posnett J (1992) The Determinants and Effects of Health Expenditure in Developed Countries. J Health Econ 11: 173-181.
- Hansen P, King A (1996) The Determinants of Healthcare Expenditure: A Cointegration Approach. J Health Econ 15: 127-137.
- Roberts J (1999) Sensitivity of Elasticity Estimates for OECD Healthcare Spending: Analysis of a Dynamic Heterogeneous Data Field. Health Economics 8: 459-472.
- Gerdtham UG, Löthgren M (2000) On Stationarity and Co-integration of International Health Expenditure and GDP. J Health Econ 19: 461-475.
- Bhargava A, Jamison DT, Lau LJ, Murray CJ (2001) Modelling the Effects of Health on Economic Growth. J Health Econ 20: 423-440.
- Freeman DG (2003) Is Healthcare a Necessity or a Luxury? Pooled Estimates of Income Elasticity from US State-level Data. Applied Economics 35: 495-502.
- Sen A (2005) Is Healthcare a Luxury? New Evidence from OECD Data. Int J Healthc Fin Econ 5: 147-164.
- Wang Z, Rettenmaier AJ (2007) A Note on Co-integration of Health Expenditure and Income. Health Economics 16: 559-578.
- Hartwig J (2008) What Drives Healthcare Expenditure? Baumol's Model of 'Unbalanced Growth' Revisited. J Health Econ 27: 603-623.
- Baumol WJ (1967) Macroeconomics of Unbalanced Growth: The Anatomy of Urban Crisis. Am Econ Rev 57: 415-442.
- Bac C, Le Pen Y (2002) An International Comparison of Healthcare Expenditure Determinants. Working Paper.
- Feldstein PJ (1988) Healthcare Economics. New York, USA.
- Gerdtham UG, Søgaard J, Andersson F, Jönsson B (1992) An Econometric Analysis of Healthcare Expenditure: A Cross-Section Study of the OECD Countries. J Health Econ 11: 63-84.
- Erdil E, Yetkiner IH (2009) The Granger-Causality between Healthcare Expenditure and Output: A Panel Data Approach. Applied Economics 41: 511-518.
- Baltagi BH, Moscone F (2010) Healthcare Expenditure and Income in the OECD Reconsidered: Evidence from Panel Data. Economic Modeling 27: 804-811.
- Freeman DG (2012) Is Healthcare a Necessity or a Luxury? New Evidence from a Panel of US State-Level Data. Working Paper.
- Magazzino C, Mele M (2012) The Determinants of Health Expenditure in Italian Regions. Int J Econ Fin 4: 61-72.
- Solow RM (1956) A Contribution to the Theory of Economic Growth. Quart J Econ 70: 65-94.
- Buchanan JM (1965) The Inconsistencies of the National Health Services. London, USA.
- Piabuo SM, Tieguhong JC (2017) Health Expenditure and Economic Growth - A Review of the Literature and an Analysis Between the Economic Community for Central African States (CEMAC) and Selected African Countries. Health Econ Rev 7: 23.
- Romer PM (1989) Human Capital and Growth: Theory and Evidence. NBER Working Paper 3173.
- Barro RJ (1992) Human Capital and Economic Growth. Federal Reserve Bank of Kansas City, USA.
- Mankiw NG, Romer D, Weil DN (1992) A Contribution on the Empirics of Economic Growth. Quart J Econ 107: 407-437.
- Pedroni P (1999) Critical Values for Cointegration Tests in Heterogeneous Panels with Multiple Regressors. Oxford B Econ Stat 61: 653-70.
- Levin A, Lin CF, Chu CS (2002) Unit Root Tests in Panel Data: Asymptotic and Finite-Sample Properties. J Econometrics 108: 1-24.
- Breitung J (2000) The Local Power of Some Unit Root Tests for Panel Data. Advances in Econometrics 15: 161-178.
- Im KS, Pesaran MH, Shin Y (2003) Testing for Unit Roots in Heterogeneous Panels. J Econometrics 115: 53-74.
- Hadri K (2000) Testing for Stationarity in Heterogeneous Panel Data. Econometric J 3: 148-161.
- Pedroni P (2004) Panel Cointegration: Asymptotic and Finite Sample Properties of Pooled Time Series Tests with an Application to the PPP Hypothesis. Econometric Theory 20: 597-625.
- Kao C (1999) Spurious Regression and Residual-Based Tests for Cointegration in Panel Data. J Econometrics 90: 1-44.
- Maddala GS, Wu S (1999) A Comparative Study of Unit Root Tests with Panel Data and a New Simple Test. Oxford B Econ Stat Special Issue: 631-652.
- Pesaran MH, Shin Y, Smith RJ (2001) Bounds Testing Approaches to the Analysis of Level Relationships. J App Econometrics 16: 289-326.
- Phelps CE, Newhouse JP (1974) Coinsurance and the Demand for Medical Services. Santa Monica, CA, USA.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi