Research Article, J Comput Eng Inf Technol Vol: 10 Issue: 8

Predicting Bit Coin Price Using Deep Learning

Yajnavalkya Bandyopadhyay^*, Tithi Mitra Chowdhury

Department of Remote Sensing, Birla Institute of Technology, Mesra, Jharkhand, India

*Corresponding Author: Yajnavalkya Bandyopadhyay
Department of Remote Sensing, Birla Institute of Technology, Mesra, Jharkhand, India
E-mail: tithimitra1508@gmail.com

Received: July 27, 2021 Accepted: August 16, 2021 Published: August 23, 2021

Citation: Bandyopadhyay Y, Chowdhury TM (2021) Predicting BitCoin Price Using Deep Learning. J Comput Eng Inf Technol 10:8.

Abstract

Keywords: Block-chain, Bitcoin, Cryptocurrency, ANN, Tensorflow, Neural networks

Introduction

Bitcoin and other forms of cryptocurrencies are blacked out in many countries like China (Baek and Elbeck, 2014) due to their characteristics of non leaving trails of money handling which forbids the laws of money handling. On the other side increasing rate of exchange between USD or INR to BitCoin exchange rates, Bitcoin has become a nice investing platform for investors as it was used to be stock market. The bitcoin prices increases with a relation in media and stock market values. Thus, bitcoin becomes one of the key element whose exchange price are important to study. Statistical Prediction models such as AR, ARMA, ARIMA [1] has already been used [2].

In this paper we propose a new model of using Deep Learning Artificial Neural Network by using TensorFlow to predict the price of Bitcoin satisfactorily. In our work we have taken values from April to August with difference of 1 minute. The Neural Network having sigmoid function with backpropagation support. Leading 80% of the data was used for training the neural network and compared to the rest 20% of the data. Our work is done on Python 3.5.3 with TensorFlow 1.5.0 to design the Deep Learning Network. The Literature for Deep Learning is very scant in the field of Cryptocurrency. With the availability of more training data and the automated pattern recognizing capabilities of Deep Learning it is becoming a better platform to test data and becoming a better and attractive replacement compared to other technicalities and models.

Technical Preliminaries : Tensorflow and Artificial Neural Network

TensorFlow is a great piece of software and currently the leading deep learning and neural network computation framework. It is based on a C++ low level backend but is usually controlled via Python. TensorFlow operates on a graph representation of the underlying computational task. This approach allows the user to specify mathematical operations as elements in a graph of data, variables and operators. Since neural networks are actually graphs of data and mathematical operations, TensorFlow is just perfect for neural networks and deep learning. Artificial Neural Networks (ANNs) require a careful selection of the input variables and network parameters such as the learning rate, number of hidden layers, and number of nodes in each layer in order to achieve satisfactory results [1]. It is also important to reduce dimensionality to improve learning efficiency. On the other hand, deep learning automatically extracts features from data and requires minimal human intervention during feature selection. Therefore, our approach does not require expertise on predictors such as macroeconomic variables and enables us to use a large set of raw-level data as input. Ignoring the factors that are known to predict the returns, our approach may not be able to outperform existing models based on carefully chosen predictors. However, considering the fast growth of deep learning algorithms, we believe this research will serve as a milestone for the future research in this direction [2,3] also predict that deep learning will play a key role in financial time series forecasting.

Related Works

The related works can be catergorized under two categories, financial and time series. financial literature, one of the relevant approaches is technical analysis, which assumes that price movements follow a set of patterns and one can use past price movements to predict future returns [4]. Caginalp and Balenovich showed that some patterns emerge from a model involving two distinct groups of traders with different assessments of valuation. Some empirically developed geometric patterns, such as heads-and-shoulders, triangle, and double-top-and-bottom, can be used to predict future price changes [5-8]. In particular, in Lo authors utilize the method of Kernel regression to identify various geometric patterns in the historical data. Price is predicted using recent history. In that sense, [5] is closest to this work. However, we note that does not yield any meaningful prediction method or for that matter eventually yield a profitable trading strategy. Our work, given the above literature, can be viewed as an algorithmic version of the “art of technical trading”. In the context of time series analysis, classical methods are a popular choice. For example, the ARIMA models which tend to capture non-stationary components through finite degree polynomials; or using spectral methods to capture periodic aspects in data, described in detail in works such as [9,10]. In contrast, our approach is nonparametric and stems from a theoretical modeling framework based on stationarity and mixing. A natural precursor to this work are [10-12]. where the nonparametric classification has been utilized for predicting trends. Classification algorithms have been used to predict stock price changes previously, e.g. Ch. 4.6.1 [13]. However, none of these works provide a theoretical framework justifying why these algorithms are suited for this problem space. Additionally, they tend to operate on a daily, weekly or monthly time-resolution which is in contrast to our goal of near real-time predictions.

Our Contribution

Our Contribution to the work is as follows:

1. Python 3.5.3 and TensorFlow 1.5.0 is used for modelling the Deep Learning Network which uses old historical data for prediction of the future values.

2. 4 hidden layers are used for the deep learning model.

3. With an interval of one minute, series of data values are collected from 1^st October-2014 followed by 1636 days data. The Neural Network having sigmoid function with backpropagation support. Leading 80% of the data was used for training the neural network and compared to the rest 20% of the data.

Testing and training data

The system shifts the each stock values by 1 minute to make the training and testing dataset exclusive so that we do not predict the current data. The testing and training data are converted to different CSV files for discriminating testing and training values.

The time series bootstrap re-sampling is used which involves repeated samples from the remainder of the seasonal decomposition of the time series in order to simulate samples that follow the same seasonal pattern as the original time series but are not exact copies of its values.

Data scaling

Most neural network architectures benefit from scaling the inputs because most common activation functions of the network’s neurons such as tanh or sigmoid are defined on the [-1, 1] or [0, 1] interval respectively. Nowadays, rectified linear unit (ReLU) activations are commonly used activations which are unbounded on the axis of possible activation values. However, sklearn’s MinMaxScaler Library Package is used in this case to easily scale the data in Python.

The testing and training data are scaled differently to avoid mutually inclusive scaling which can cause errors in prediction.

Optimizer

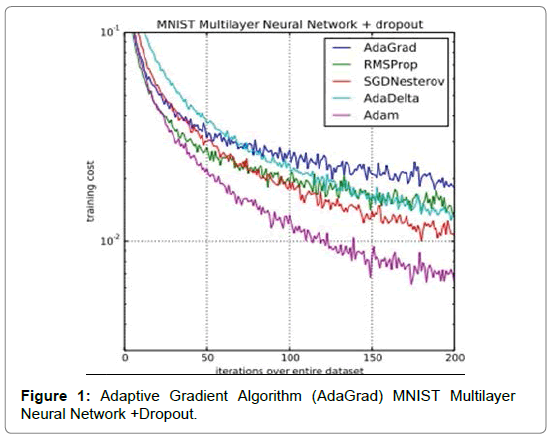
The optimizer is used for necessary computations for network weight and bias variables during training. This tool indicates the direction of the gradient which indicates the direction of the weights and biases have to be changed to minimize the network cost function. Here Adaptive Gradient Algorithm (AdaGrad) which is a stochastic algorithm, which is used that maintains a per- parameter learning rate that improves performance on problems with sparse gradients Figure 1.

Designing the network

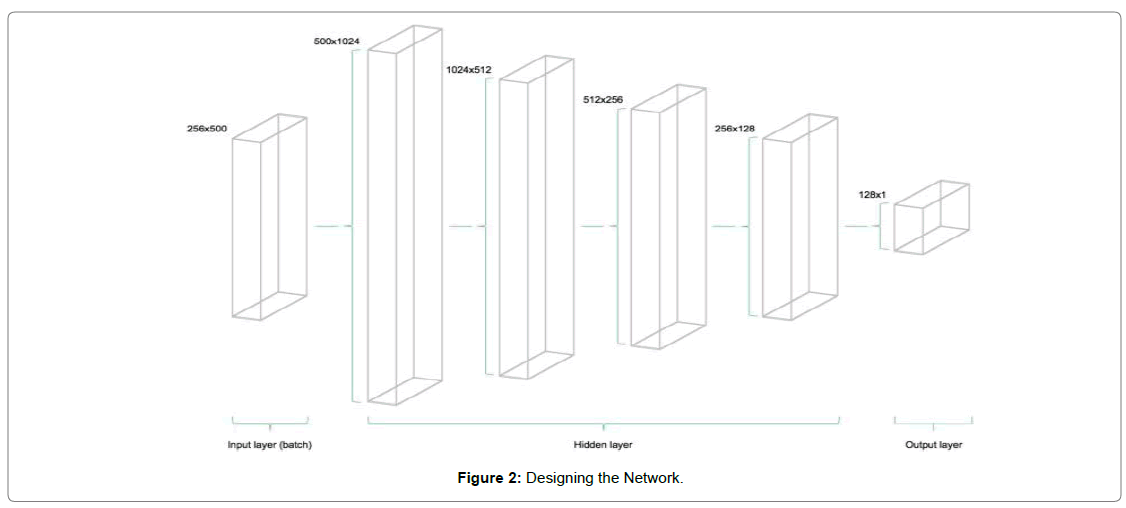
The Neural network is designed keeping the model having 4 hidden layer where the number of Neurons are decreased by halving the Neuron numbers from 1024,512,256 and 128 respectively in respective hidden layer to compress the data and finally one output neuron as Placeholder for output Figure 2.

Cost Function

The cost function of the network is used to generate a measure of deviation between the networks predictions and the actual observed training targets. For regression problems, the mean squared error (MSE) function is commonly used. MSE computes the average squared deviation between predictions and targets. Basically, any differentiable function can be implemented in order to compute a deviation measure between predictions and targets. The MSE function in mathematical equation obeys as follow:

E=1(h(x)-Y_i)²

Where h(x) stands for mean value of the data and yⁱ stands for the i^th value.

Optimizer

After having defined the placeholders, variables, initializers, cost functions and optimizers of the network, the model needs to be trained. Usually, this is done by minibatch training. During minibatch training random data samples of n = batch size are drawn from the training data and fed into the network. The training dataset gets divided into (n /batch size) batches that are sequentially fed into the network. At this point the placeholders X and Y come into play. They store the input and target data and present them to the network as inputs and targets. A sampled data batch of X flows through the network until it reaches the output layer. There, TensorFlow compares the models predictions against the actual observed targets Y in the current batch. Afterwards, TensorFlow conducts an optimization step and updates the networks parameters, corresponding to the selected learning scheme. After having updated the weights and biases, the next batch is sampled and the process repeats itself. The procedure continues until all batches have been presented to the network. One full sweep over all batches is called an epoch. The training of the network stops once the maximum number of epochs is reached or another stopping criterion defined by the user applies.

Results

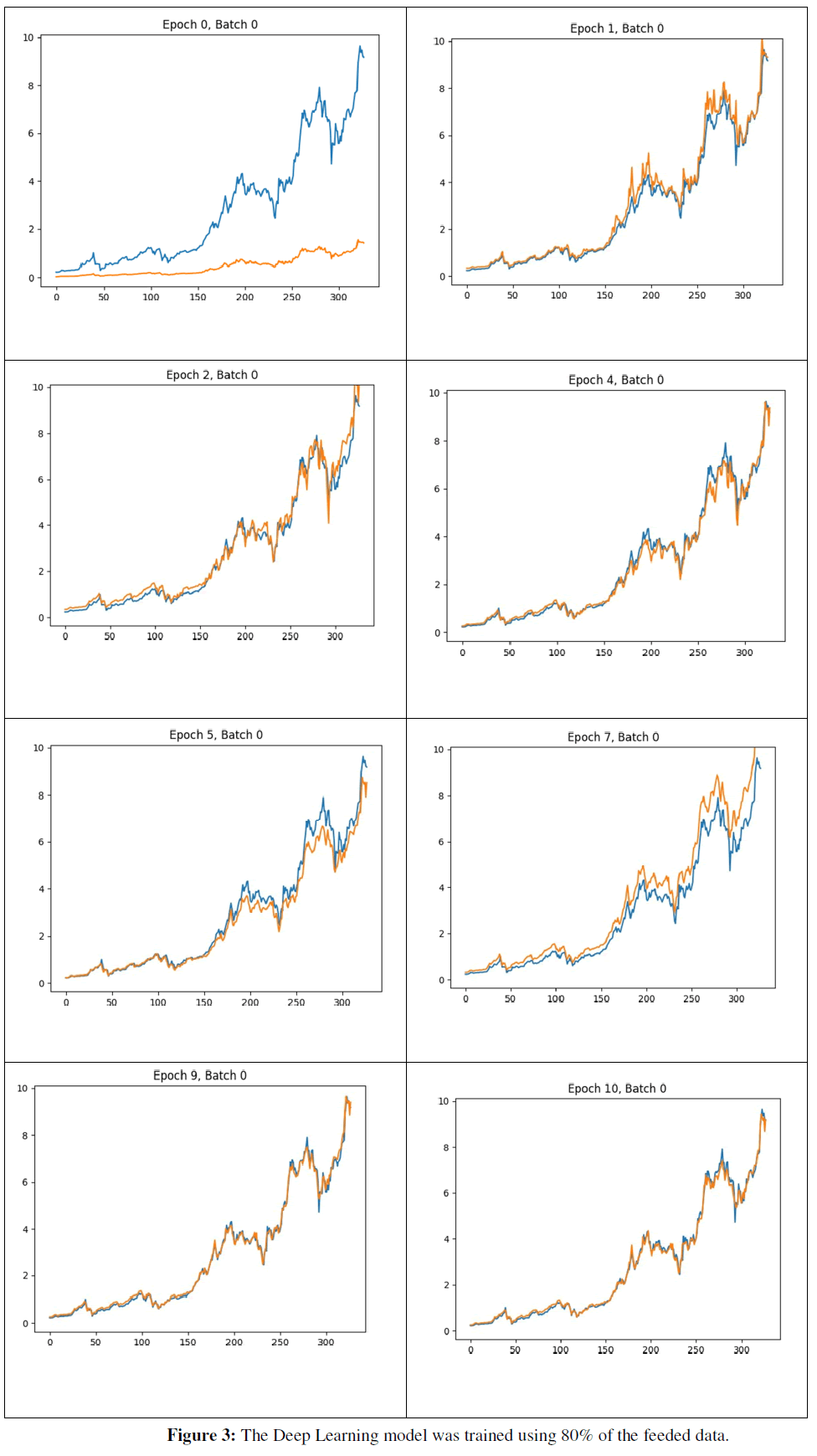
The Deep Learning model was trained using 80% of the feeded data. Rest 20% was predicted using the model and compared with the original data. On performing that we get the following result where blue colored graph indicates the actual data and yellow colour indicates the predicted data. The absicca and the ordinate in the graphs shows time variant and Price respectively. A full epoch is completing the training for 100 batches where the model runs to solve the model of the graph. After a few epoch we get the model prediction comes close to the original data Figure 3. Upon running with the provided settings these training results in each epoch and batches we get the following graph at epoch intervals.

Conclusion and Future Scope of Work

The paper deals with the model which works only on historical dataset. The model can be made more robust by providing of the changing data sets such as media news, stock market dataset, etc. No doubt the model works better than the statistical time series models which fail on the self-learning and back propagation support.

References

1. Amjad M, Devarat S (2017) Trading Boitcoin online using time series prediction. Proceedings of the Time Series Workshop at NIPS 2016, PMLR 55: 1-15.
2. Alrasheedi  M (2012) Predicting up/down direction using linear discriminant analysis and logit model: The case of sabic price index. Res J Bus Manag 6: 121-133.
3. Brockwell P, Davis R (2013) Time series: theory and methods. Sci Bus Media.
4. Dobra I, Adriana A (2008) Modelling unemployment rate using box-jenkins procedure. J Applied Quantitative Methods.
5. James G, Witten D, Hastie T, Tibshirani R (2013) An Introduction to Statistical Learning.
6. Rahman M, Islam S, Nadvi M (2013) Comparative study of ANFIS and ARIMA model for weather forecasting in Dhaka. International Conference on Informatics, Electronics and Vision (ICIEV).
7. David S, Robert H (2015) Time Series Analysis and its Applications. Blue Printing, 3rd edition.
8. Devavrat Shah and Kang Zhang. Bayesian regression and bitcoin. CoRR 2014.
9. Brodersen KH, Gallusser F, Koehler J, Remy N, Scott SL (2015) Inferring causal impact using bayesian structural time- series models. Ann Appl Stat 9(1): 247-274.
10. Franco P (2014) Understanding Bitcoin: Cryptography, engineering and economics, John Wiley & Sons 288.
11. George EI, McCulloch RE (1993) Variable selection via Gibbs sampling. J Am Stat Assoc 88(423): 881-889.
12. Kim YB (2016) Predicting fluctuations in cryptocurrency transactions based on user comments and replies. Plos One 11(8): 1-18.
13. Tibshirani R (1996) Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society Series B(Methodological) 58(1): 267-288.