Research Article, J Comput Eng Inf Technol S Vol: 0 Issue: 1
Sudden Cardiac Death Detection Methods Based on ECG Biometric Technologies
| Shen T*, Shen H, Lin C and Ou Y | |
| Department of Medical Informatics, Tzu Chi University, Hualien, 97004 Taiwan | |
| Corresponding author : Tsu-Wang Shen, Ph.D Associate Professor / Stanford-Taiwan Biomedical Fellow (STB), Department of Medical Informatics, Tzu ChiUniversity, Address: 701, Sec. 3, Jhong-Yang Rd. Hualien, 97004, Taiwan Tel: +886-3-8565301, Ext: 2382 Fax: +886-3-8579409 E-mail: tshen@mail.tcu.edu.tw, biom3.lab@gmail.com |
|
| Received: February 10, 2016 Accepted: May 02, 2016 Published: May 09,2016 | |
| Citation:Shen T, Shen H, Lin C, Ou Y (2016) Sudden Cardiac Death Detection Methods Based on ECG Biometric Technologies. J Comput Eng Inf Technol. S1-002. doi:10.4172/2324-9307.S1-002 |
Abstract
Sudden Cardiac Death Detection Methods Based on ECG Biometric Technologies
Sudden cardiac death (SCD), which occurs when there is an abrupt loss of heart function, has caused millions of deaths worldwide. The aim of our study was to detect SCD occurrence and provide SCD warnings by using ECG biometric algorithms. Two methods of detection were analysed, comprising modified zero-crossing and wavelet based methods. An average heartbeat was generated for each person by randomly selecting 20 normal sequential heartbeats to become their heartbeat template. For the modified zero-crossing method, when the SCD event correlation coefficients dropped substantially because of waveform dissimilarity, the threshold for a suspected SCD event was set at 0.7. After the correlation coefficients dropped below the threshold, an IIR filter with a center frequency of 5 Hz and the zero-crossing method were applied to further verify SCD events. Overall, the results showed that our algorithm successfully detected up to 98.48% accuracy. The wavelet method detected SCD events by using template similarities and wavelet coefficient plots. The wavelet analysis was applied to detect SCD with an overall performance of a 92.31% correct detection rate. Hence, this study demonstrated the possibility of developing an all-in-one system for monitoring life-threatening heartbeats while protecting personal medical data.
Keywords: Sudden cardiac death; ECG biometrics; Template matching; Zerocrossing; Wavelets transform
Keywords |
|
| Sudden cardiac death; ECG biometrics; Template matching; Zerocrossing; Wavelets transform | |
Introduction |
|
| Sudden cardiac death (SCD) is an unexpected natural death from a cardiac cause in a very short term period. The onset of symptoms occurs generally more or less than 1 hour before leading to sudden fatal death. It is reported that SCD occur in 300,000 to 400,000 individuals a year in the USA and millions of deaths worldwide. Approximately 1%-2% of patients survive SCD when it occurs outside a hospital [1]. Additionally, a victim of SCD may not even have been diagnosed with heart disease. Furthermore, SCD typically occurs unexpectedly [2]. | |
| SCD is most often initiated by a sustained ventricular tachyarrhythmia, such as ventricular tachycardia (VT), ventricular flutter (VFL), or ventricular fibrillation (VFib). A smaller percentage of SCD events are related to a primary bradyarrhythmia. | |
| Tompkins and Afonso showed how the short-time Fourier transform, the smoothed pseudo-Wigner–Ville distribution, and a cone-shaped kernel distribution were used to classify normal and shockable rhythms [3]. Jekova and Krasteva developed a real-time detection algorithm for ventricular fibrillation and tachycardia [4]. An SCD detector should include an electrocardiogram (ECG) identity verification function, so that SCD events can be identified easily when ECG waveforms suddenly change. Previous research demonstrated the details of how an ECG-based biometric system works to identify people by combining a template matching method with a distance discrimination method or various other artificial neural networks [5]. ECG biometric technology was not only used to personalize medical devices to establish personal data profiles but also to potentially reduce complexities on ECG monitors for distinguishing normal from abnormal heartbeats [4]. | |
Methodology |
|
| SCD database | |
| The SCD Holter Database is a collection of long-term ECG recordings of patients who experienced SCD while being recorded. The database contains 23 complete Holter recordings from which half-hour excerpts are available to researchers. The database currently comprises 18 patients who had an underlying sinus rhythm, 1 who was continuously paced, and 4 who had atrial fibrillation. All patients had a sustained ventricular tachyarrhythmia and most of them had an actual cardiac arrest. Moreover, our normal subject database is included for this study with 42 randomly selected volunteers who were mostly (41) normal healthy individuals and 1 cardiac vascular disease (CVD) patient for evaluate possible false alarm case [6]. | |
| For each recording, only 4-minute ECG signals (2 minutes both before and after VF onset time) were kept in our SCD database to simulate SCD events that occurred immediately after normal heart rhythms. In addition, these recordings provided samples of up to 500 Hz. However, three recordings with no VF onset time were excluded from our SCD database. Our modified biometric technology [7] was then applied to detect any SCD events. In this study, an ECG biometric algorithm was applied to detect and identify SCD events. | |
| Template matching for SCD pre-processing | |
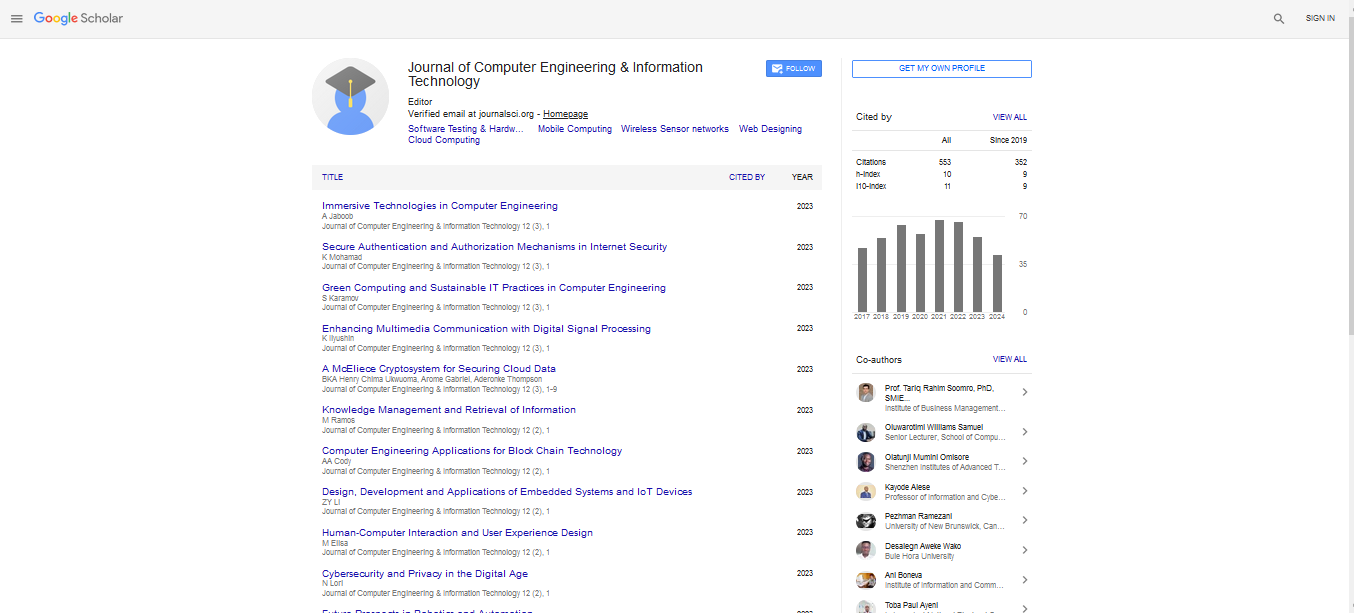
| Two signals are classified as correlated if the respective shapes of the waveforms of each signal match one another. The correlation coefficient shows how similar or dissimilar the signals appear. The equation of the correlating coefficient is shown as follows: | |
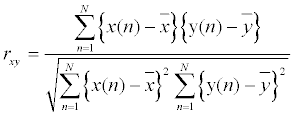 (1) (1) |
|
| In the enrollment process, an average heartbeat was generated for each person by randomly selecting 20 of their normal and sequential heartbeats to be their heartbeat template. If a normal heartbeat is not available, the general heartbeat template is applied. The heartbeat template represented the identity of each person. The template matching was then applied on each heartbeat that was input. This technique of correlating one signal with another requires the two signals to be aligned with one another. Because the template must be correlated with the incoming signal, the signal should be aligned with the template. For each person, the correlation coefficients between their template and their normal heartbeats were typically very close to 1. When SCD occurs, abnormal heartbeats are extremely dissimilar from the person’s normal heartbeats, causing the correlation coefficients to drop substantially. In Figure 1, the upper figure shows a real-time SCD event that contained three normal heartbeats followed by life-threatening heartbeats; the lower figure shows the correlation coefficients between the person’s ECG template and the real-time ECG signals. | |
| Figure 1: Correlation coefficients drop substantially when SCD starts. | |
| Modified zero-crossing method | |
| According to the established knowledge of ECG biometrics, if the correlating coefficient between template and input ECG signals is lower than 0.7, the probability of the two ECG patterns being from the same person is very low. Hence, in this proposed method, the threshold (TH) for a suspected SCD event is set at 0.7. If the correlation coefficients drops below the TH for 4 seconds, an IIR filter with a center frequency of 5 Hz and the zero-crossing method are applied to further verify SCD events, where the zero-crossing method is to count the number of the sign of a mathematical function changes Finally, if the counter numbers continually remain higher than the upper TH (HI=8) or equal to the lower TH (LO=0) for 8 seconds or above, the system activates an SCD alarm, which is defined as a successful detection on one SCD event. Figure 2 summarizes the block system diagram for detecting SCD events. | |
| Figure 2: Block system diagram for detecting SCD events. | |
| The frequency domain of VFib and VFL covers a frequency of 2-7 Hz [3,8]. Our IIR filter is designed with a center frequency of 5 Hz and a bandwidth of 2 Hz to enhance detection of the lifethreatening ECG arrhythmias and suppress detection of the normal sinus rhythm. Figure 3a shows that the normal heartbeats of our samples were followed by VF. After the IIR filter was employed, the ventricular arrhythmias were considerably enhanced by comparing them with normal heartbeats. In this case, the SCD event would have more zero-crossing points than regular heartbeats do, making the waveform look more complex than normal heartbeats. However, VF and bradyarrhythmia may cause markedly fewer zero-crossing points than normal rhythms do because of low amplitudes or very slow rhythms. Hence, the modified zero-crossing method is applied to the ECG waveform to measure its complexity. | |
| Figure 3: (a & b): The SCD recording shows that the normal heartbeats were followed by ventricular arrhythmias. (b) After employing the IIR filter, the ventricular arrhythmias were enhanced by comparing them with normal heartbeats. | |
| The regular zero-crossing method cannot be directly applied to ECG waveforms without pre-processing. As shown in Figure 3b, because of an artifact, P waves, and T waves, the normal heartbeats had a complexity similar to that of the life-threatening heartbeats close to 0 mV. In the proposed method, it is therefore necessary to eliminate the center (close to 0 mV) area in Figure 3b as the pre-processing step. | |
| To detect complexity, first, a 2-second processing window is randomly set to determine the amplitude of an R wave. The maximum value, located at an R wave in general, is multiplied by 0.7 to yield the first TH, TH1. The ECG signal is then shifted, on the basis of TH1, to eliminate the center area, as mentioned previously. Second, all the negative values are set to 0 and all positive values remain unadjusted. Finally, the zero-crossing method and a counter are applied. The detailed procedure used to determine the waveform complexity is shown in Figure 4. | |
| Figure 4: Determining the waveform complexity. | |
| Figure 5a illustrates how the input ECG is subtracted from TH1 to avoid yielding an indistinguishable center area. Equation (2) is applied to translate x[i] to ±1 signals, as shown in Figure 5b. | |
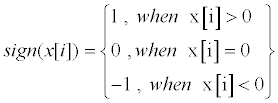 (2) (2) |
|
| Figure 5: (a & b): Filtered ECG is shifted by TH1. (b) The translation of x[i] to ±1 signals is performed to count the number of zero crossings. | |
| where x[i] is the result of filtered ECG signals which substitute the second TH, TH2, and TH2 is the median number of Figure 5a, excluding the SCD events. | |
| The computer program calculates the number of zero-crossings within a 3-second window. The window then moves 1 second at a time. Additionally, the counter is set to record the number of changes when +1 switches to -1 or -1 switches to +1. For a normal heart rhythm, the counter number shows approximately three for each 3-second window. However, for SCD events, the counter number is typically higher than the TH [9], or remains at 0. If this situation occurs for 8 seconds, the SCD alarm will be activated. Please refer to Figure 6 for more details. | |
| Figure 6: (a & b):Correct detection of an SCD event with most of the life-threatening heartbeats marked. (b) The modified zero-crossing method was used for a complexity check. (c) The zero-crossing counter must remain high for 8 seconds to activate the SCD alarm. | |
| Wavelets analysis for SCD detection | |
| For signal denoising, a least-squares polynomial low-pass filter with the difference equation | |
| y(n) = ((1/429) * (-36x(n-10) +9x(n-9) + 44x(n-8) + 69x(n- 7) + 84x(n-6) + 89x(n-5) + 84x(n-4) + 69x(n-3) + 44x(n-2) + 9x(n- 1) - 36) and a hi-pass IIR filter with the difference equation y(n) = 1-2x(n-1) + x(n-2) + 1.994y(n-1) -0.994y(n-2) is applied to limit the ECG bandwidth between 1 Hz and 50 Hz. | |
| An ECG biometric template must then be made before
distinguishing individuals. To generate ECG templates, 90-second
ECG signals can be recorded and QRS complexes can be recognized
by our program. The recognized R-waves are utilized as markers to
divide one heartbeat by shifting from 180 sampling points to the left
and 200 of them to the right. The interval should include most of the
P–QRS–T waves, and the length of template should be fixed. Finally,
after 20 single normal heartbeats have been produced, the median
heartbeat can be calculated as an ECG biometric template. The median heartbeat indicates that the median values of each element of
20 ECG vectors (from |
|
| In accordance with Shen’s ECG biometric method [7], the template
is compared with real-time ECG signals by calculating the correlation
coefficient |
|
| where Xi is a ECG template and Yi is a real-time heartbeat. In equation (4), the similarity score (SS) for each heartbeat is used to evaluate both waveform similarity and amplitude differences by dividing the correlation coefficient and MSE. A higher SS represents a higher matching possibility. | |
| Similarity score (SS) = |
|
| Finally, after 10% of SS outliers are excluded, the averaged similarity score indicates the user’s identification. After a personal match is achieved using the SS, the wavelet transforms not only provide the relation of time and frequency but also demonstrate the relation of time and scale. In this study, these characteristics were used to detect SCD events. First, the ECG data that included both the normal heart rhythm and the SCD event was translated with Daubechies wavelets (db2). The scale coefficients Ca,b , were then calculated using equation (5). | |
 (5) (5) |
|
| where Y(t) is the ECG signal and |
|
| Figures 7 and 8 show that in this study, the luminescent spots of the scale of SCD events were more numerous than those of the normal heart rhythm. To make the illuminant spots more distinguishable, the wavelet plots were binarized, as shown in Figures 7 and 8d. The white pixels per time unit were then computed to distinguish between normal and SCD events. | |
| Figure 7: (a & b): Normal heart rhythm (8 seconds). (b) Frequency coefficient plot for normal rhythm. (c) Scale plot for normal rhythm. (d) Binary plot for normal rhythm. | |
| Figure 8: (a) The SCD event (8 seconds). (b) Frequency coefficient plot for SCD. (c) Scale plot for SCD. (d) Binary plot for SCD | |
| At a normal heart rhythm condition, the number of white pixels per second for each person varies. Because our system involves an identity verification function, the number of white pixels per second for each person can be determined by averaging 30 second of white pixels. The TH is then set, through equation (6), to recognize SCD events and 10 logD is utilized for data normalization. | |
| TH= |
|
| Therefore mentioned process can be performed when people enroll in the system. Subsequently, all input ECG signals can be used to calculate the values of log (white pixels / second) 10 for monitoring SCD events. When these 10 log values remain higher than the TH for more than 7 seconds, the SCD alarm will be activated. As shown in Figure 9, our program marked most of the life-threatening heartbeats and the SCD alarm was activated successfully. | |
| Figure 9: (a) The SCD event was correctly detected and most of life-threatening heartbeats were marked. (b) The illuminant spots of the SCD event (posterior) were more condensed than those of the normal one (forepart). (c) Binary image of both events. | |
Results and Discussion |
|
| For the modified zero-crossing method, the 23 SCD samples from PhysioBank (SCD Holter Database) and our normal subject database (42 samples: 41 normal and 1 CVD) were used to detect the SCD events. The CVD patient was considered as a high risk SCD subject. However, when only template matching methods were implemented to detect SCD events, 4 of 24 (numbers 37,43,47 and 52) could not be detected correctly. Hence, the template matching method cannot detect a SCD event alone. | |
| After combining the template matching and modified zero-crossing, the modified zero-crossing method was applied to cross-check the SCD events. The results showed that the algorithm successfully detected up to 95.83% of SCD occurrences (23 of 24 events). The data of one event (sample 43) could not be correctly detected because the sample did not cross the threshold of 0.7. If the normal database is included, the overall accuracy is reached to 98.48% (64/65). | |
| For the wavelet detection method, when wavelet transform was applied to the MIT–BIH SCD Holter Database, 5 of 23 (numbers 33, 41, 48, 51 and 52) could not be detected correctly. Figure 10 (numbers 52) shows an example for incorrect detection on SCD event. In this case, the muscle noise influenced the wavelet detection method. The developed system had a 92.31% (60/65) correct detection rate (accuracy) for the two databases. | |
| Figure 10: The SCD (number 52) event was not correctly detected because of noisy condition. | |
Conclusion |
|
| Our research thus far has demonstrated that ECG biometric technology can be used to identify SCD events through two different methods. The modified zero-crossing method provided a 98.48% accuracy rate, thus demonstrating higher performance than that of the wavelet analysis. It must be noticed that the CVD patient showed SCD pattern because of arrhythmia. The system is implemented as a real-time system in Figure 11, including a data acquisition card (National Instrument DAQ-6024E), a shielded (noise rejecting) connection box (NI BNC-2110), LabViewTM, and MATLABTM software with our self-made ECG amplifier [10]. | |
| Figure 11:A real-time SCD detector based on ECG biometric technology. | |
| This study demonstrated the possibility of developing an allin- one biometric system for monitoring SCD life-threatening events while protecting personal medical data. However, when ECG biometric elements become involved, the complexity of the health care privacy system may be reduced [11,12]. Typically, an abnormal physiology status is a status of a certain degree of difference in comparison with that person’s known and normal status or other people’s statuses. Hence, if a person’s normal status is determined known, then an unhealthy status is considerably easier to detect. | |
References |
|
|
|
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi