Research Article, J Chem Appl Chem Eng Vol: 2 Issue: 1
The Simms Constants as Parameters in Hyperbolic Functions Related to Acid-Base Titration Curves
Anna Maria Michalowska-Kaczmarczyk1, Aneta Spórna-Kucab2, Agustin Garcia Asuero3 and Tadeusz Michalowski2*
1Department of Oncology, The University Hospital in Cracow, 31-501 Cracow, Poland
2Department of Analytical Chemistry, Technical University of Cracow, 31-155 Cracow, Poland
3Department of Analytical Chemistry, The University of Seville, 41012 Seville, Spain
*Corresponding Author : Tadeusz Michałowski
Faculty of Chemical Engineering and Technology, Cracow University of Technology, Warszawska 24, 31-155 Cracow, Poland
Tel: +48126282035
E-mail: michalot@o2.pl
Received: January 01, 2018 Accepted: January 01, 2018 Published: February 02, 2018
Citation: MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A, Asuero AG, MichaÅ‚owski T (2018) The Simms Constants as Parameters in Hyperbolic Functions Related to Acid-Base Titration Curves. J Chem Appl Chem Eng 2:1. doi: 10.4172/2576-3954.1000111
Abstract
The Simms constants (gi) are parameters of transformed equations for acid-base titration curves, obtained from rational functions of the Padé type. The relationships between gi and successive dissociation constants Ki values for polyprotic acids are formulated. The models related to acid-base titration curves are expressed in terms of hyperbolic functions. Some relations of gi to the Fermi- Dirac distribution function are indicated.
Keywords: Acid-base equilibria; Titration curves; Hyperbolic functions
Notations
D – titrand, gi – Simms constant; T – titrant
Introduction
The term ‘Simms constants’ is an eponym related to virtual equilibrium constants (gi) suggested by Simms [1-5], known also as ‘titration indices’ or ‘titration constants’ [6,7]. The gi were considered first in biological context [8-10], and later in a series of papers involved with titrimetric methods of analysis [11-15]. In particular, the gi concept can be applied in modeling the equilibria occurred in complex acid-base systems, where the isomolarity condition was fulfilled [16,17]. Later on, the Simms constants were applied to modeling of titration curves perceived from the viewpoint of total alkalinity (TAL) [18-20], also with fulvic acids (FA) involved [19]. The Simms can be considered [16-24] in context of rational functions of the Padé type [25], with activity h of H+1 ions as the variable.
Application of the Simms constants enables any q-protic acid HnL (C0 mol/L), characterized by successive dissociation constants (Ki) values [10,16], to be considered as a mixture of q weak monoprotic acids HL(k) (k = 1, …,q) of the same concentration, i.e., C0 mol/L; the Simms constants gi are ascribed to these acids as (virtual) dissociation constants. The relations between gi and Ki values were formulated. Mathematical transformations made for this purpose resemble the technique called as decomposition of rational functions into a sum of partial fractions, well-known to students during the course in mathematical analysis (integral calculus), see e.g. [26]. The Simms constants are involved in the partial fractions of this kind.
In this paper, the Simms constants (gi) will be referred to D+T systems, with MmHn-mL (C0) + HB (Ca) + MOH (Cb) solution, called as the sample tested (ST), see Table 1. Depending on the pre-assumed composition of the species formed in a system, we consider first the more general case where complexes of MaHiBbL+a+i-b-n type are formed; a, b = 0,1,…, i.e., the species HiL+i-n (i=0,…,q) are also admitted here (at a=b=0). The D+T system where only the species HiL+i-n (i=0,…, q) are formed, is considered as a particular case of the more complex system of the species. The interrelations where hyperbolic functions are involved with parameters of this simpler system, with dissociation constants (Ki) or stability constants of proto-complexes (KiH), known from tables of equilibrium data, are presented here. Stability constants of the mixed complexes are rarely met in literature; see e.g. [27-30].
| System no. | ST | HB (CB) | MOH (CM) | MB (CMB) | F | ||||
|---|---|---|---|---|---|---|---|---|---|
| D | T | D | T | D | T | D | T | ||
| 1 | VST | VST | – | VB | – | – | VMB | V*MB | 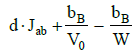 |
| 2 | VST | VST | VB | – | – | – | V*MB | VMB | 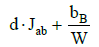 |
| 3 | VST | VST | – | – | – | VM | VMB | V*MB | 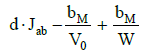 |
| 4 | VST | VST | – | – | VM | – | V*MB | V*MB | 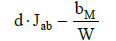 |
Table 1: Composition of titrand (D) and titrant (T) for different isomolar systems and the related expressions for F (Eq. 6); W = V0+V.
Composition of titrand (D) and titrant (T)
The D and T are prepared in volumetric flasks: F1 and F2, each with a volume of Vf mL. First, equal volumes VST of a sample tested composed of MmHn-mL (C0) + HB (Ca) + MOH (Cb) are introduced into F1 and F2. In turn, VB mL of HB (C) or VM mL of MOH (C) is added into F1. Then V*MB mL of MB (CMB) is introduced into F1, and VMB mL of MB (CMB) is introduced into F2. The volumes V*MB and VMB of MB fulfill the optional relations:
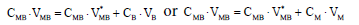 (1)
(1)
(see Table 1). Both flasks are then supplemented with distilled water to the mark, and mixed thoroughly.
The volume V0 mL (V0 ≤ Vf) is taken for analysis and titrated as D with T, added in portions; V mL is the total volume of T added from the beginning of the titration to a given point of the titration. The value
W = V0+V (2)
is the total volume of D+T system, at a given point of titration.
Formulation of D+T system
Denoting [MaHiBbL+a+i-b-n ] =caib for brevity, and applying the notations:
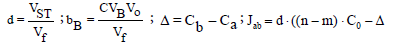 (3)
(3)
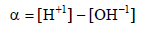 (4)
(4)
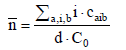 (5)
(5)
from addition of balances:
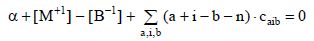
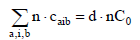
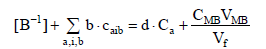
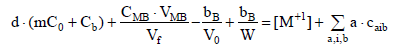
we get the relation
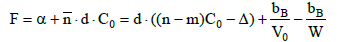 (6)
(6)
(see Table 1). The relations for F in the systems 2 – 4 are obtained similarly. (Equation 6) can be transformed into the form
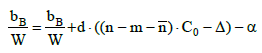 (7)
(7)
Note that
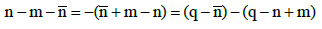 (8)
(8)
where :
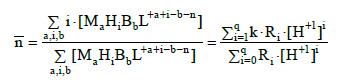 (9)
(9)
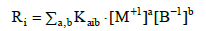 (10)
(10)
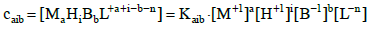 (11)
(11)
Applying (8) in (7), we have
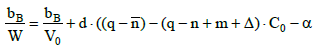 (12)
(12)
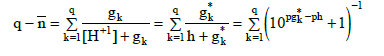 (13)
(13)
A Simpler System
The simpler case is the system, where the species HiL+i-n (i=0,…,q) are formed in the D+T mixture. These species can be characterized, optionally, by (successive) dissociation constants, Kj (j = 1,…,q):
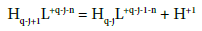
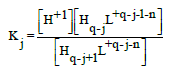 (14)
(14)
or by stability constants KiH of the related proto-complexes, HiL+i-n,
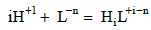
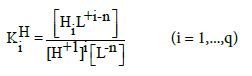 (15)
(15)
Then we get the relations
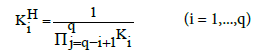 (16)
(16)
Applying (15) in the relation
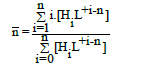 (17)
(17)
we have
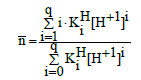 (18)
(18)
The Simms constants gk are interrelated with successive dissociation constants Kj (Equation 14) of the acid HnL considered; we have a set of interrelations:
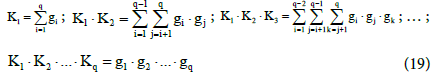
The expression for 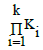 (in Equations 19), formulated for q-protic acid, is a sum involving
(in Equations 19), formulated for q-protic acid, is a sum involving
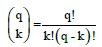 (20)
(20)
components [19] formed from k different gi values. In particular, for H3PO4 (acid of H3L type, q=n=3):
at k=1 we have 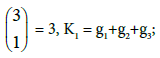
at k=2 we have 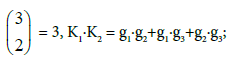
at k=3 we have 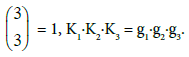
Generalizing, the binomial coefficient 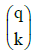 [31] (Equation 20) expresses the number of distinct k-element subsets, formed from a set containing q different elements [32], as in the Pascal’s triangle [33].
[31] (Equation 20) expresses the number of distinct k-element subsets, formed from a set containing q different elements [32], as in the Pascal’s triangle [33].
The gi values can be calculated, provided that KiH (Equation 16) or Ki (Equation 14) values are known beforehand. Such calculations can be done with use of the iterative computer programs [34], as one specified in [19]. In particular,
• for H2CO3 (q = 2): pK1 = 6.3, pK2 = 10.1, we have: pg1 = 6.300069, pg2 = 10.099931;
• for H3PO4 (q = 3): pK1 = 2.1, pK2 = 7.2, pK3 = 12.3, we have: pg1 = 2.100003, pg2 = 7.200000, pg3 = 12.299997.
As we see, pgi ≈ pKi values are here not distant from values. The differences | pgi – pKi | are greater when pKi values for a polyprotic acid are closer to each other.
For comparative purposes, we consider V0 mL of titrand D containing a mixture of q weak monoprotic (qk=nk=1) acids HL(k) (C0k; k=1,…,q), titrated with V mL of (a) HB (C) or (b) MOH (C) as T, we get the equations:
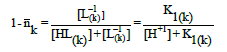 (21)
(21)
and then
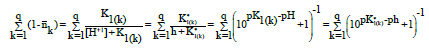 (22)
(22)
where: 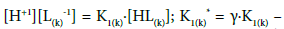 the related hybrid dissociation constants,
the related hybrid dissociation constants, 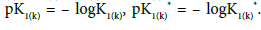 Then we have
Then we have
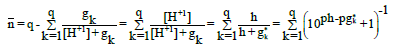 (23)
(23)
The Relative Contents of the Components Constituting D and T
The D and T include sample tested, ST (Table 1). If CMB >> Σa,i,b caib then [M+1] and [B-1] values are practically constant during the titration. Moreover, we assume 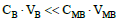 . Similar composition of D and T guarantees the stability of ionic strength of the solution. The relative permittivity ε is also kept constant if the D and T compositions are similar; it makes also the volumes additivity more accurate than when mixing various aqueous solutions. Then the isomolarity condition (Equation 1) enables to keep approximately constant values of the equilibrium constants, under isothermal conditions.
. Similar composition of D and T guarantees the stability of ionic strength of the solution. The relative permittivity ε is also kept constant if the D and T compositions are similar; it makes also the volumes additivity more accurate than when mixing various aqueous solutions. Then the isomolarity condition (Equation 1) enables to keep approximately constant values of the equilibrium constants, under isothermal conditions.
Therefore, the values of Ri (in Equation 10) or Ki (in Equation 18) are practically constant during the titration carried out under such conditions. The hydrogen ion activity coefficient γ = γH+1 has also a stable value. The titration in isomolar systems makes it possible to determine γH+1 as one of the physicochemical parameters of the system, along with other equilibrium constants values [17].
Formulation in terms of Hyperbolic Functions
The related formulas can be expressed in terms of hyperbolic functions [35]. For this purpose, we denote: z = ln10∙pH, w = ln10∙pKW, sk = log10∙pgk. Then applying the identity
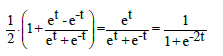 (24)
(24)
we get:
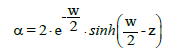 (25
(25
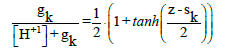 (26)
(26)
From Equation 8, 13, 26 we have
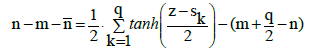 (27)
(27)
The formulas involved with ph and gk* look alike. From Equations: 12, 13, 25 and 26, for C0k = C0, we get
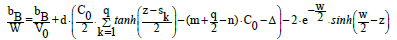 (28)
(28)
The hyperbolic functions can also be applied to more complex acid-base systems, discussed in [18-20,37].
Rational Functions
The general form of a rational function of variable x [37], y = y(x), is the quotient of polynomials p(x) and q(x), i.e.
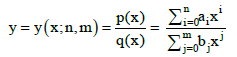 (29)
(29)
where m ≥ 1, i.e., the denominator q(x) involves explicitly the variable x.
The titration curves related to isomolar systems can be presented in the form of rational functions of the Padé type [16,17,20-24]. For example, for the mixture HL (C0) + HB (Ca) applied as ST in the system 3, we obtain the function
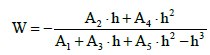 (30)
(30)
where: A1 = ∙ KW∙x0γ3 ; A2 = bM∙x0∙γ2 ; A3 = (KW + d∙(C0 + Ca – aM/ V0)∙x0)∙γ2; A4 = bM∙γ ; A5 = (d∙(Ca – aM/V0) – x0)∙γ, aM = bM/d; x0 = 1/ K1, where [H+1][L-1] = K1∙[HL]; the activity of hydrogen ions, x = h, is the variable in Eq. 30.
Special cases of rational functions are Möbius transformations [38]. The rational functions were also applied in different methods of chemical analysis, namely: in modified Gran methods of titrimetric analyses [39-43], for calibration curve, and standard addition methods [44-47].
Acid-base Micro-Equilibria as Emanation of Stochastic Processes
On the basis of formulation with the Simms constants involved one can state that the dissociation of H+1 from different protonation sites/centers proceeds independently, and the proton uptake/ dissociation from/to these sites (basicity centers) can be perceived as a stochastic process, categorized in terms of a success/failure. The degree of dissociation HL(k) = H+1 + L(k)-1 from the k-th site is
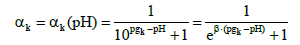 (31)
(31)
where β = ln10. The αi = αi(pH) fulfills the properties of cumulative distribution function
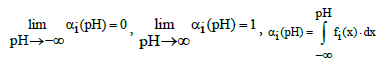 (32)
(32)
where y = fi(pH) is the probability density function
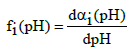 (33)
(33)
It implies that [19]
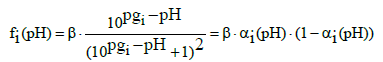 (34)
(34)
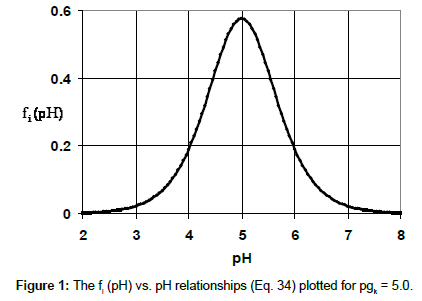
The function (34) plotted in Figure 1 appears some similarities with the Fermi-Dirac distribution function [48].
Final Comments
The paper presents formulation of acid-base titration curves of different degree of complexity, for the D+T systems prepared according to unconventional mode, where D and T are prepared in accordance with the principle of isomolar solutions, suggested and formulated first time in the papers [16,17,21-24]. This procedure, where D and T have similar composition, secures constancy of equilibrium constants, activity coefficient of H+1 ions, and relative permittivity of D+T system during the titration performed under isothermal conditions.
Assuming formation of the species of (i) HiL+i-n or (ii) MaHiBbL+a+ib-n type (i = 0,…,q) formed by an acid HnL in the system where the species M+1 and B-1 are also involved, the relations involving the mean number of protons, Ížn (Eq. 9 or 18) attached to the basic form L-n and the Simms constants gk were formulated. The partial ratios involved with gk were expressed in terms of the hyperbolic tangent (tanh) functions. The α (Eq. 4) was expressed in terms of hyperbolic sine (sinh). The partial ratios (Eq. 26) have the form (Eq. 34) similar to the one related to the density function in the Fermi-Dirac distribution function. Moreover, in [49], the inverse hyperbolic function argsinh [50] was applied for titration curve related to argentometric titration, and inverse hyperbolic function argcosh [50] as applied [28-30,52] for other titrations.
It were also proved that the titration of HnL (C0) with MOH is equivalent to titration of the mixture of q monoprotic acids, HL(i) (C0), with the related dissociation constants gk = K1k = [H] [L(k)] /[ HL(k) . In other words, application of Simms constants principle provides a kind of ‘homogenization’, where polyprotic acids are transformed into the mixture of monoprotic acids. It is a very important property, especially advantageous when considered in context with titration of solutions whose composition and then acid-base properties are unknown a priori, e.g., fulvic acids. It particularly refers to determination of total alkalinity of natural (e.g. marine) waters, wastes and different beverages, made according to titrimetric mode (pH titration).
References
- Simms HS (1926) Dissociation of polyvalent substances I. Relation of constants to titration data. J Am Chem Soc 48: 1239-1250.
- Simms HS (1926) Dissociation of polyvalent substances II. Relation of constants to chemical structure. J Am Chem Soc 48: 1251-1261.
- Simms HS, Levene PA (1926) Graphical interpretation of electrometric titration data by use of comparison curves. J Biol Chem 70: 319-325.
- Levene PA, Simms HS (1926) Nucleic acid structure as determined by electrometric titration data. J Biol Chem 70: 327-341.
- Simms HS (1930) The arginine and prearginine groups in edestin. J General Physiol 14: 87-97.
- Muralt AL (1930) The titration constants of multivalent substances. J Am Chem Soc 52: 3518-3523.
- Greenstein JP (1932) The titration constants of α,β-diaminopropionic acid and their relation to the constants of various isomers. JBiol Chem96: 499-510.
- Harris LJ (1929) The combination of proteins, Aminoacids, &c., with Acids and Alkalis. Part II. Titration Curves of Amino-acids in presence of formaldehyde. Proceedings of the Royal Society of London, Series B, Containing Papers of biological Character, 104: 412-439.
- Edsall JT, Wyman J (1958) Biophysical Chemistry: Vol. I, Thermodynamics, Electrostatics, and the Biological Significance of the properties of matter. Academic Press Inc Publishers, New York, USA.
- Dixon HB, Clarke SD, Smith GA, Carne TK (1991) The origin of multiply sigmoid curves of pH-dependence: The partitioning of groups among titration pK values. Biochem J 278: 279-284.
- Klas J (1968) General formula for the calculation of the hydrogen ion concentration of aqueous solutions of several polyvalent weak acids. Analytica Chimica Acta 41: 549-550.
- Gamble DS (1970) Titration curves of fulvic acid: the analytical chemistry of a weak acid polyelectrolyte. Canadian J Chem 48: 2662-2669.
- Klas J (1975) Calculation of the stability constants of complexes with respect to Simms’ conception of dissociation of polyvalent acids. Analytica Chimica Acta 74: 220-222.
- Johansson S (1979) Simplification of the mathematical evaluation of titration results by regarding complexes of the type AnB as n complexes of the type AB. Analyst 104: 593-600.
- Johansson A, Johansson S (1979) Automatic titration by stepwise addition of equal volumes of titrant. Part IV. General-purpose program for evaluating potentiometric acid-base titrations. Analyst 104: 601-612.
- Michałowski T (1992) Some new algorithms applicable to potentiometric titration in acid-base systems. Talanta 39: 1127-1137.
- Michałowski T, Gibas E (1994) Applicability of new algorithms for determination of acids, bases, salts and their mixtures. Talanta 41: 1311-1317.
- Asuero AG, Michałowski T (2011) Comprehensive formulation of titration curves referred to complex acid-base systems and its analytical implications. Critical Reviews in Analytical Chemistry 41(2): 151-187.
- Michałowska-Kaczmarczyk AM, Michałowski T (2016) Application of Simms Constants in Modeling the Titrimetric Analyses of Fulvic Acids and Their Complexes with Metal Ions. J Solution Chem 45: 200-220.
- Michałowski T, Asuero AG (2012) New approaches in modelling the carbonate alkalinity and total alkalinity. Crit Rev Anal Chem 42: 220-244.
- Michałowski T, Rokosz A, Tomsia A (1987) Determination of basic impurities in mixture of hydrolysable salts. Analyst 112: 1739-1741.
- Michałowski T (1988) Possibilities of application of some new algorithms for standardization purposes; Standardization of sodium hydroxide solution against commercial potassium hydrogen phthalate. Analyst 113: 833-935.
- MichaÅ‚owski T, Rokosz A, Negrusz-SzczÄ™sna E (1988) Use of Padé approximants in the processing of pH titration data; Determination of the parameters involved in the titration of acetic acid. Analyst 113: 969-972.
- MichaÅ‚owski T, Rokosz A, KoÅ›cielniak P, ÅÂÂagan JM, Mrozek J (1989) Calculation of concentrations of hydrochloric and citric acids together in mixture with hydrolysable salts. Analyst 114: 1689-1692.
- Safe EB (1977) Pade and Rational Approximation. Theory and Applications, Elsevier Inc.
- Partial fraction decomposition. Wikipedia.
- Janecki D, Michałowski T (1999) Evaluation of equilibrium constants- A new approach. Chemia Analityczna 44: 611-621.
- Janecki D, Doktór K, MichaÅ‚owski T (1999) Determination of stability constants of complexes of MiKjHkL type in concentrated solutions of mixed salts. Talanta 48: 1191-1197.
- Janecki D, Doktór K, MichaÅ‚owski T (1999) Erratum to determination of stability constants of complexes of MjKjHkL type in concentrated solutions of mixed salts. Talanta 49: 943.
- Janecki D, Styszko-Grochowiak K, Michałowski T (2000) The catenation and isomerisation effects on stability constants of complexes formed by some diprotic acids. Talanta 52: 555-562.
- Binomial coefficient. Wikipedia.
- Combinatorics. Wikipedia.
- Pascal's triangle. Wikipedia.
- Michałowski T (2011) Application of GATES and MATLAB for resolution of equilibrium, metastable and non-equilibrium electrolytic systems, In: Applications of MATLAB in science and engineering. Michałowski T (Ednt.) InTech, Rijeka, Croatia, 1-34.
- Hyperbolic function. Wikipedia.
- Michałowska-Kaczmarczyk AM, Michałowski T (2015) Dynamic buffer capacity in acid-base systems. J Solution Chem 44: 1256-1266.
- Rational Function. Wikipedia.
- Möbius transformation. Wikipedia.
- Michałowski T, Baterowicz A, Madej A, Kochana J (2001) An extended Gran method and its applicability for simultaneous determination of Fe(II) and Fe(III), Analytica Chimica Acta 442: 287-293.
- Michałowski T, Toporek M, Rymanowski M (2005) Overview on the Gran and other linearization methods applied in titrimetric analyses. Talanta 65: 1241-1253.
- Michałowski T, Kupiec K, Rymanowski M (2008) Numerical analysis of the Gran methods. A comparative study. Analytica Chimica Acta 606: 172-183.
- Ponikvar M, Michałowski T, Kupiec K, Wybraniec S, Rymanowski M (2008) Experimental verification of the modified Gran methods applicable to redox systems. Analytica Chimica Acta 628: 181-189.
- Pilarski B, Michałowska-Kaczmarczyk AM, Asuero AG, Dobkowska A, Lewandowska M, Michałowski T (2014) A New approach to carbonate alkalinity. J Analytical Sci, Methods Instrumentation 4: 62-69.
- Michałowski T, Pilarski B, Ponikvar-Svet M, Asuero AG, Kukwa A, Młodzianowski J (2011) New methods applicable for calibration of indicator electrodes. Talanta 83: 1530-1537.
- Gorazda K, Michałowska-Kaczmarczyk AM, Asuero AG, Michałowski T (2013) Application of rational functions for standard addition method. Talanta 116: 927-930.
- Michałowski T, Pilarski B, Michałowska-Kaczmarczyk AM, Kukwa A (2014) A non-linearity criterion applied to the calibration curve method involved with ion-selective electrodes. Talanta 124: 36-42.
- Michałowska-Kaczmarczyk AM, Asuero AG, Martin J, Alonso E, Jurado JM, Michałowski T (2014) A uniform nonlinearity criterion for rational functions applied to calibration curve and standard addition methods. Talanta 130: 307-314.
- Fermi–Dirac statistics. Wikepedia.
- Michałowski T, Stępak R (1985) Evaluation of the equivalence point in potentiometric titrations with application to traces of chloride. Analytica Chimica Acta 172: 207-214.
- Inverse hyperbolic functions. Wikipedia.
- Janecki D, Michałowski T (1999) Evaluation of equilibrium constants- A new approach. Chemia Analityczna 44: 611-621.
- MichaÅ‚owski T, Baterowicz A, Wójtowicz A (2000) Sources of error in b-correction spectrophotometry. Talanta 52: 337-340.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi