Research Article, J Chem Appl Chem Eng Vol: 2 Issue: 1
Theoretical and Experimental Investigation on Granulation Processes of Powdered Materials in Cylindrical Granulator
Kelbaliyev GI1, Mammadova GM2, Samadli VM1, Talibov NH3, Samedov MM3* and Ahmadov VN3
1M.Naqiev Institute of Catalysis and Inorganic Chemistry, Azerbaijan National Academy of Sciences, Baku, Azerbaijan
2Azerbaijan State University of Oil and Industry, Azerbaijan
3Sumgayit State University, Sumgayit, Azerbaijan
*Corresponding Author : M. M. Samadov
Department of Chemistry, Sumgayit State University, Sumgayit, Azerbaijan
E-mail: samedov-muxtar@mail.ru
Received: January 12, 2018 Accepted: February 07, 2018 Published: February 19, 2018
Citation: Kelbaliyev GI, Mammadova GM, Samadli VM, Talibov NH, Samedov MM, et al. (2018) Theoretical and Experimental Investigation on Granulation Processes of Powdered Materials in Cylindrical Granulator. J Chem Appl Chem Eng 2:1. doi: 10.4172/2576-3954.1000112
Abstract
The problems of experimental and theoretical investigation and analysis of granulometric composition of granules in granulation processes of powdered superphosphates in drum apparatus are considered. The theoretical investigation has been constructed on analytical decision of Fokker-Planck stochastic equation defining evolution of the distribution function of granules on sizes.
Keywords: Granulation; Powdered; Strength; Porosity; Superphosphate; Moistening
Introduction
The processes of granule formation of powdered materials are widely used in chemical, food and pharmaceutical industries. It can be noted that various methods of granulation of powdered materials (rolling, fluidization, mixing, pelletization) [1-3] among which, thanks to the big productivity, granulation by rolling in drum apparatus are widely expanded in the chemical industry. The mechanism of granule formation is difficult, and includes following stages: nucleation and granule growth as a result of powder lamination, consolidation with extrusion of binding agent to a surface, deformation of form, deterioration of a surface as a result of mutual friction, crushing and other physical phenomena which influences formation of granule of the end size of strength and porous structure. As a result of action of a set of the interrelated factors, the formed granules of the various sizes are characterized by polydispersity of composition with a definite average dispersion.
Knight et al. and Ceylan et al. have been devoted to the experimental investigation of formation of granules of polydisperse composition and connected with it, distribution of granules on sizes, measurement of their sizes and porosity [2,4-6]. The experimental curves of distribution of granules on sizes in mixers-granulators showed their double-humped character of distribution curve maximums of which are determined in the field of nucleation and in the field of structure formation of granule. In drum devices the most effective is a description of evolution of probability function of granule size distribution with the use of Fokker-Planck stochastic differential equation [6,7] on the base of experimental data characterizing continuous lamination and growth granule. At the same time, it will be noted that a distribution of granules on sizes can depend on character of distribution of sizes of drops of binding agent.
The aim of this work is the experimental and theoretical investigation of the evolution of granules distribution on sizes and on length of apparatus in the granulation process of powdered materials in drum device.
Basic factors influencing on polydispersity of granules
In the process of granule formation, various factors influence on the final sizes: sizes of drops of binding agent, crushing and deterioration of granules, character of their consolidation in drum devices and many other factors. As a result of the influence of these factors, a disperse composition of granules is changed in each section and along the length of drum device which leads to evolution of the distribution function of granules on sizes. On formation of nucleus and granules as a whole an essential influence is shown by the sizes of drops of the binding agent, connected with character of crushing of liquid by air depending on forces, connected with a velocity head and surface capillary forces. A decay of the binding agent on conglomerate of fine drops and their fall on surface of powdered material influences on sizes of nuclei in the process of granule formation. The work by Levich VG denotes that the size of drops forming as a result of decay of liquid is inversely proportional to Weber number [8]
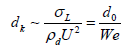 (1)
(1)
where 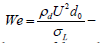 Weber number, dk - size of forming drops, U -feed rate of liquid, d0 - equivalent size of drops, ρc - density of medium, σL -surface tension. After liquid dispersion in air flow drops are recrushed for more fine ones. On the basis of experimental investigations by Peri J, within the limits of the taken designations the Nikuyama-Tanasava formula has been proposed [9]
Weber number, dk - size of forming drops, U -feed rate of liquid, d0 - equivalent size of drops, ρc - density of medium, σL -surface tension. After liquid dispersion in air flow drops are recrushed for more fine ones. On the basis of experimental investigations by Peri J, within the limits of the taken designations the Nikuyama-Tanasava formula has been proposed [9]
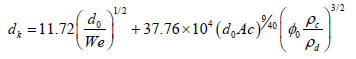 (2)
(2)
where 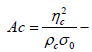 Acrivos number,
Acrivos number,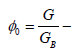 mass fraction, G, GB - mass expenses of liquid and air. In this empirical formula the following units of measure have been taken: dk and d0 (μm), ρd и ρc (g/cm3), σ (dn/cm) and ηc (poise). In works by Sarimeseli et al., Sis et al. and Kelbaliev et al., a frequency of crushing of drops in isotropic turbulent flow has been determined [10-12]
mass fraction, G, GB - mass expenses of liquid and air. In this empirical formula the following units of measure have been taken: dk and d0 (μm), ρd и ρc (g/cm3), σ (dn/cm) and ηc (poise). In works by Sarimeseli et al., Sis et al. and Kelbaliev et al., a frequency of crushing of drops in isotropic turbulent flow has been determined [10-12]
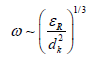
In literature there are a set of empirical formulas determining an average size of drops at decay of stream. With increase of sizes of drops of the binding agent a probability of preparation of granules of large sizes grows. Such distribution of sizes of drops of the binding agent creates conditions for formation of granules from very small sizes to large sizes up to formation of lumps, i.e. generates definite polydispersity.
The numerous experimental investigations of granulation processes in mixing devices-granulators [1-6] and in drum devices [6-10] showed that a final size of granules is determined by a set of parameters among which it is important to note the size of formed nucleus-germ, size of particles of powder and drops of the binding agent, conditions of agglomeration, properties of powder and liquid and from method of granulation. Bouwman et al. proposed influence of particle sizes of drops of the binding agent on formation, morphology of structure and further granule growth are considered. Lamination thickness and conditions of completeness of structure of granule are determined by moisture capacity or wettability of surface [3,4,13-15]. In this connection, Abberger et al. and Hapgood et al. propose the influence of sizes of drops on growth rate and investigated the formation of nuclei in granulators–mixers. Infiltration time of a liquid is entered into layer of powder, so-called penetration time and defined as [16,17]
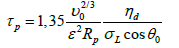
where υ0 − volume of liquid drop, θ0 - wetting angle, σL - surface tension of liquid.
It will be noted that a prediction of corresponding quantity of liquid (size of drop) to prepare the desirable granule size is very difficult because, besides factors indicated above, the sizes of forming granules depend on the adhesive properties of powder, and on physical properties of liquid (viscosity, density, surface tension). The final granule size is determined by retentivity of wetted surface and character of change of lamination thickness. If the granule surface possesses minimum moisture content, the further powder lamination on surface also becomes minimal, i.e. lamination thickness tends to zero.
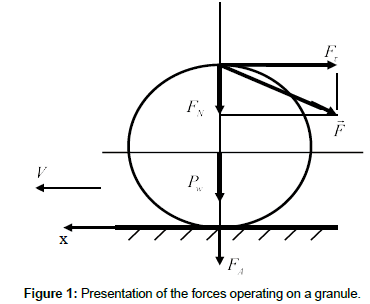
Significant impact on granule size is observed by ware in the result of friction wall surface of apparatus and between itself (Figure 1). Resultant force vector which is functioning on granule surface is equal to:
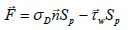 (3)
(3)
By projecting force vector 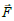 on the axis coinciding with direction of movement, we obtain
on the axis coinciding with direction of movement, we obtain
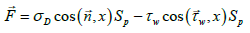
In a particular case, putting 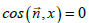 and
and 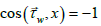 , from this equation, we have
, from this equation, we have
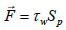 (4)
(4)
Here 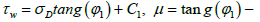 friction module, 0.3 ≤ μ ≤ 0.6. Then from equation (4) we get
friction module, 0.3 ≤ μ ≤ 0.6. Then from equation (4) we get
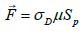
We identify linear ware of granule surface as
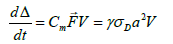 (5)
(5)
Where γ = Cmγπψ , Cm - coefficient, depending on properties of wall and granule material, Sp =ψπ a2. ψ − proportion of granule surface, set with a wall and a layer of powder. As follows from equation (6), the wear rate is proportional to the square of the size and speed of movement. The more the size of granule, the more the rate of production. Taking into account the anisotropy of the granule’s shape [14], a mechanism and model for the formation of granules in the drum apparatus are proposed, which with a slight effect of wear is converted to form [15].
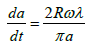 (6)
(6)
where a − average granules size, t-stay time. Along with aggregation, the process of granule formation is accompanied by crushing. A set of experimental work found laws of crushing, each of which is known to be right only in the field of sufficiently rough dispersity. Many of them can be expressed by the following, empirically established ratio
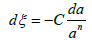
Where ξ - specific energy, reported to unit of volume of destroyed material, n, C- coefficients characterizing properties and destruction energy. In particular, at n=1 from this expression we will prepare the destruction law of fragile material
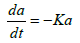 (7)
(7)
where 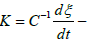 coefficient, depending on bond strength of aggregates of material and law of change of specific energy of crushing. Having connected the equations (6) and (7), we will prepare the general expression characterizing the process of granule formation taking into account granules crushing
coefficient, depending on bond strength of aggregates of material and law of change of specific energy of crushing. Having connected the equations (6) and (7), we will prepare the general expression characterizing the process of granule formation taking into account granules crushing
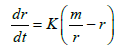 (8)
(8)
Here 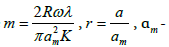 average granule size. Equation (5) characterizes a change of average granules size taking into account lamination and crushing, analytical solving of which can be presented as
average granule size. Equation (5) characterizes a change of average granules size taking into account lamination and crushing, analytical solving of which can be presented as
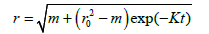 (9)
(9)
Equation (5) can be used for investigation and analysis of character of distribution of polydisperse granules at granulation of powdered materials.
Experimental investigation of granulometric composition
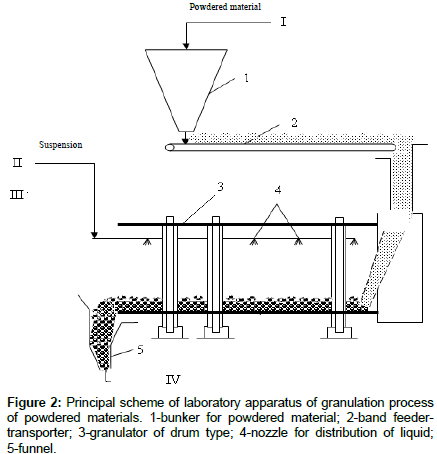
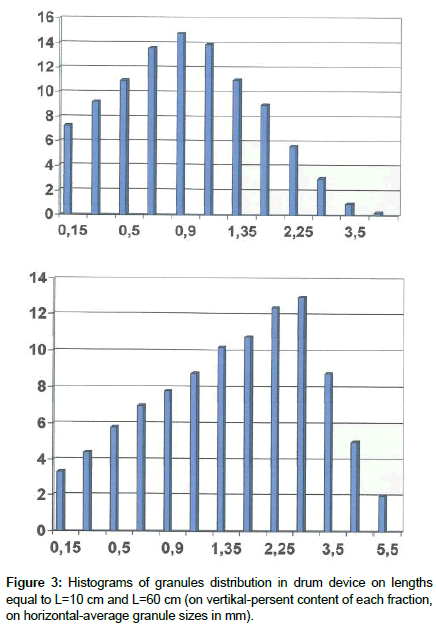
The experimental investigations of granulometric composition of superphosphate granules were carried out on samples prepared in laboratory drum granulator with diameter 2R=12 cm, with length L=80 cm, angular velocity of rotation ω=30 min-1 and degree of filling Ψ=15% (Figure 2). In a drum granulator for moistening of powdered superphosphate by means of nozzles the binding agent (suspension composition: 18-20% natural ceolit; 5-6% NH4OH; 74-77% H2O in a quantity (G=6×10-3m3/h) was supplied. On length of drum device on distances L=10,20,40,60,80 cm the samples of granules by weight of 200 grams were selected. Later on, each sample was dried at temperature T=90-100°C for 1-1.5 h and the samples were riddled through a sieve (13 pieces) by sizes from 0.1-6.0 mm and fractions corresponding to definite ranges of sizes were weighted. The experimental values of sieve analysis on measure of each fraction in masses and mass fractions are presented in Table 1 (here mg - mass of granules of definite size in each sieve, Ï• - mass fraction). In Figure 3 it has been presented the histogram of granule distribution on length of drum device which gives evident interpretation of overall picture in the device. An average granule size for each length of device was determined according to the formula
| Fractions sizes, mm | 0,1-0,2 | 0,2-0,4 | 0,4-0,6 | 0,6-0,8 | 0,8-1,0 | 1,0-1,2 | 1,2-1,5 | 1,5-2,0 | 2,0-2,5 | 2,5-3,0 | 3,0-4,0 | 4,0-5,0 | 5,0-6,0 |
| L=10 cм mg, g. φ |
14,63 0,073 |
18,53 0,092 |
21,95 0,109 |
27,3 0,136 |
29,75 0,198 |
27,80 0,139 |
22,40 0,110 |
18,00 0,090 |
11,20 0,056 |
5,850 0,030 |
1,950 0,0097 |
0,480 0,0024 |
0,0 0,0 |
| L=20 cм mg, g. φ |
9,870 0,049 |
11,80 0,060 |
15,10 0,075 |
17,70 0,089 |
19,73 0,098 |
22,37 0,110 |
26,30 0,130 |
25,00 0,125 |
21,60 0,108 |
21,60 0,108 |
9,20 0,046 |
6,0 0,03 |
0,350 0,003 |
| L=40 cм mg, g. φ |
4,680 0,023 |
7,80 0,039 |
10,10 0,050 |
13,30 0,066 |
14,80 0,074 |
17,20 0,0859 |
20,30 0,10 |
21,80 0,109 |
25,00 0,125 |
25,00 0,125 |
20,30 0,101 |
14,84 0,074 |
6,20 0,03 |
| L=60 cм mg, g. φ |
6,600 0,0329 |
8,800 0,044 |
11,70 0,058 |
13,90 0,07 |
15,40 0,078 |
17,60 0,088 |
20,50 0,102 |
21,90 0,109 |
24,90 0,184 |
26,4 0,130 |
17,59 0,088 |
10,25 0,050 |
4,30 0,02 |
| L=80 cм mg, g. φ |
2,890 0,014 |
4,340 0,0217 |
6,520 0,0326 |
8,700 0,043 |
10,10 0,050 |
14,50 0,072 |
18,0 0,09 |
19,50 0,0975 |
20,60 0,103 |
28,80 0,144 |
30,78 0,154 |
22,40 0,112 |
12,450 0,0625 |
Table 1: Experiental granules disfribution on sizes and on length of device.
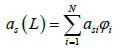
where N - number of intervals of measurement. Using equation (8), the equation for estimation of average granule size distribution on length of the device is:
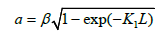 (10)
(10)
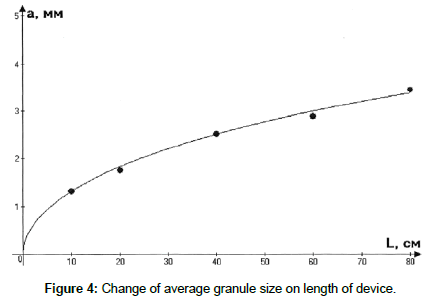
Here 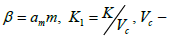 average rate of displacement of granules on length of device. In Figure 4 a change of average size of superphosphate granules on length of device is presented (β=5.5, K1=0.00588).
average rate of displacement of granules on length of device. In Figure 4 a change of average size of superphosphate granules on length of device is presented (β=5.5, K1=0.00588).
Use of Fokker-Planck equation for construction of evolution of the distribution function of granules
The basis of description of evolution of probability function of distribution of granules on stay time and on sizes at continuous change of sizes is the Fokker-Planck stochastic equation [6,7], which taking into account an equation (8) will be as
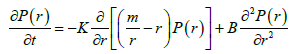 (11)
(11)
In the assumption of constancy of lamination thickness and coefficient of stochastic diffusion B, a general solution (11) by method of variables separation will be as [6,7]
 (12)
(12)
Here
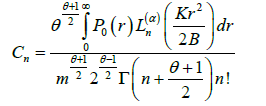 (13)
(13)
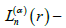 Laguerre polynomial n-degree of order
Laguerre polynomial n-degree of order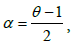
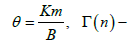 Gamma function,
Gamma function, 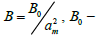 coefficient of stochastic diffusion. The solutions (9) and (10) are very complex for practical applications. From these equations we will determine the established value of distribution function at t→∞
coefficient of stochastic diffusion. The solutions (9) and (10) are very complex for practical applications. From these equations we will determine the established value of distribution function at t→∞
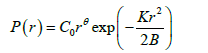 (14)
(14)
Here 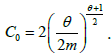 From equation (14), the established value does not depend on the initial distribution. If granulation rate is much more than crushing rate (m→∞), then the series shown in (Eqn. 12) converges rapidly. At large values of crushing rate of granules such state is reached at smaller values of t. The average granules size taking into account
From equation (14), the established value does not depend on the initial distribution. If granulation rate is much more than crushing rate (m→∞), then the series shown in (Eqn. 12) converges rapidly. At large values of crushing rate of granules such state is reached at smaller values of t. The average granules size taking into account 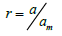 will be determined as
will be determined as
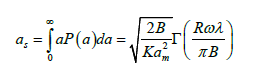 (15)
(15)
Maximums of distribution (14) correspond to relation of granule formation rate to crushing rate
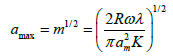 (16)
(16)
The more crushing rate, the smaller the values of maximums of distribution function are reached, i.e. granules prepared are more diffuse. Judging by experimental investigations, a crushing of granules takes place basically in average part of the device. Lamination thickness λ on surface of granules is not constant value, and depends on sizes of particles of powder, on the content of the binding agent in granule and on physical phenomena of consolidation and deterioration. In particular, in work by Kelbaliev GI this mechanism is considered as consolidation of elastically connected particles of powder in volume of singular granule [18]. As a result of consolidation of granule under action of external pressure and weight of overlying layers, the binding agent is superseded from open-ended pores to granule surface, thereby, increasing probability of sticking of particles of powder and growth of lamination thickness. The lamination thickness is also influenced by granule crushing, character of distribution of supplying of the binding agent on length of the device and many other factors. The lamination thickness is proportional to the area of surface of granule and the size of granule, the large moisture of surface and ability to powder lamination. This fact stipulates a change of distribution coefficients (Eqn. 14) on length of drum device which can be presented as
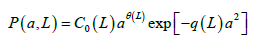 (17)
(17)
where 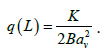 Using experimental data on granules distribution we will determine
Using experimental data on granules distribution we will determine
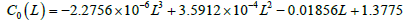
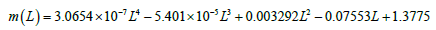
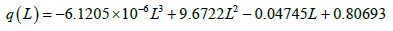
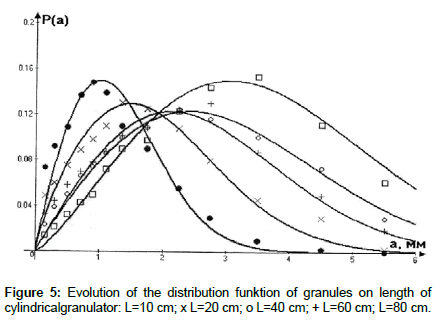
Where L-current length, in cm. In Figure 5 the evolution of the distribution function of granules on sizes and on length of device is presented, the calculation curves correspond to Eqn. 17. The experimental and theoretical investigations allow analyzing character of scatter and distribution of granules on sizes and on the length of device. The presented curves of distribution are asymmetric for each section with characteristic maximums and are not subjected to any standard types of distribution.
In the particular case, the form of the function (Eqn. 14) is close to Rosen-Rambler distribution, if θ =1- is close to Rayleigh distribution, and if θ =2- is close to Maxwell distribution. In practical calculations, in view of the arbitrariness of θ, the form of the distribution function differs from the known standard functions.
Influence of deformation and consolidation of granules on character of their distribution
Granule has a porous structure, pores of which have been filled with binding agent, connecting particles of powder in uniform system. As a result of its rolling with lamination of particles of powder on surface and consolidation under action of external tensions a final creation of porous structure of granule characterized by definite strength takes place. Granules are friable structures which under action of external forces and weight of overlying layers can be subjected to deformation, i.e. to change of form. At a volume current the solid phase of porous granule flows into granule pore, compressing poral liquid (binding agent) and displacing it on continuous and open-ended poral channels. If in low-permeability or impenetrable medium the isolated closed ensembles of interrelated pores are included then a volume current leads to increase of pressure of liquid in pores, which finally can also lead to destruction and deformation of granules. The mechanism of consolidation and deformation of granules under action of external deforming tensions leading to change of density and porosity is the ambiguous function of many parameters [7,18]. The experimental investigations on formation and deformation of granules in stirring devices were presented by Bouwman [3]. Rhodes proposed the equation for estimation of Stokes deformation in his work [19]
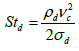
By analogy with number We for deformable liquid drops and bubbles, we will enter deformation number for deformable porous solid particles
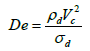 (18)
(18)
Where σd - surface tension characterizing strength of granule. A value σd - can be determined on formula [19]
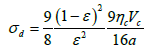
A number De characterizes a relation of force of external action to force characterizing a tension on surface of granule. Evidently, if De << 1, a granule corresponding to large values of surface strength is not subjected to deformation. At values De << 1 a granule is subjected to deformation and takes the shape of an oval, an ellipse (in section), and also other wrong forms which are indefinable and essentially influencing on evolution of the distribution function. Powder lamination to surface of a granule occurs until concentration of binding agent on surface does not become minimal. The processes of lamination and consolidation proceed simultaneously and interrelatively, in connection of which a description of these phenomena is rather difficult. The more the granule is consolidated, the more binding agent is forced away to a surface and, hence, the more lamination thickness. Practically it is impossible to estimate a change of lamination thickness on length of drum device experimentally. At the same time an availability of experimental and theoretical curve of distribution or experimental change of average size can be used for solution of reverse incorrect problem of estimation of lamination thickness at known other parameters and measurements. An estimation of lamination thickness can be carried out on the following criteria
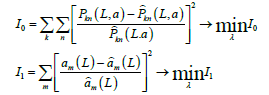 (19)
(19)
where 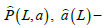 are experimental values of the distribution function and average granules size. As the definition problem of λ by the first criterion (Eqn. 19) is incorrectly stated, it is necessary to determine the area of regularity of its solution. One of the possible determinations of area of regularity can be prepared by the methods of theory of errors from expressions (Eqn. 14) and (Eqn. 17) as
are experimental values of the distribution function and average granules size. As the definition problem of λ by the first criterion (Eqn. 19) is incorrectly stated, it is necessary to determine the area of regularity of its solution. One of the possible determinations of area of regularity can be prepared by the methods of theory of errors from expressions (Eqn. 14) and (Eqn. 17) as
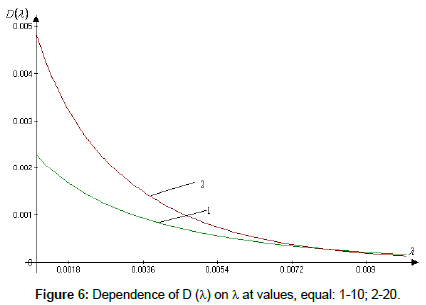
δλ = D(λ )δ P (20)
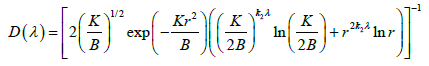
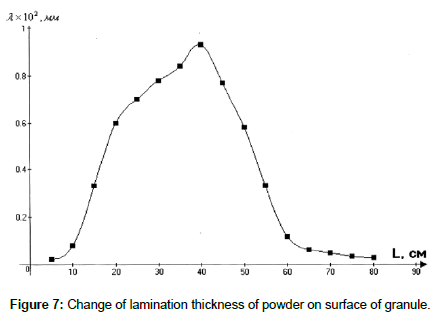
where 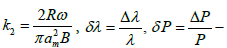 relative errors in definitions of λ and P; Δ λ, ΔP - absolute errors. Thus, an area of regularity for expression λ =Φ-1(P) is determined from equation (20) under condition of sufficient smallness δλ, depending on value D(λ). In Figure 6 a change D(λ). From λ depending on values K/B is presented. As follows from Figure 6, in the field of 10-3 ≤ λ ≤ 10-2 mm with increase of relation K/B, D(λ) is decreased, i.e. for sufficiently small values δP, a problem of estimation λ can be considered conditionally correct. The results of estimation of lamination thickness on second criterion (Eqn. 16) are presented in Figure 7, which shows that large value of lamination thickness of powder is reached only in the middle of drum device (L=20-60 cm) and essentially falls to escaping from device. Nucleation, lamination, consolidation and deformation are the basic physical processes in formation process and formation of granules of definite disperse composition and can show an essential influence on character of the distribution function.
relative errors in definitions of λ and P; Δ λ, ΔP - absolute errors. Thus, an area of regularity for expression λ =Φ-1(P) is determined from equation (20) under condition of sufficient smallness δλ, depending on value D(λ). In Figure 6 a change D(λ). From λ depending on values K/B is presented. As follows from Figure 6, in the field of 10-3 ≤ λ ≤ 10-2 mm with increase of relation K/B, D(λ) is decreased, i.e. for sufficiently small values δP, a problem of estimation λ can be considered conditionally correct. The results of estimation of lamination thickness on second criterion (Eqn. 16) are presented in Figure 7, which shows that large value of lamination thickness of powder is reached only in the middle of drum device (L=20-60 cm) and essentially falls to escaping from device. Nucleation, lamination, consolidation and deformation are the basic physical processes in formation process and formation of granules of definite disperse composition and can show an essential influence on character of the distribution function.
Results and Conclusions
The investigations carried out in this work have been devoted to the analysis of granulometric composition in granulation process of powdered materials on sizes and on length of drum devices. It has been noted that an essential influence on granule formation is shown by the distribution of drops of binding agent and also physical processes of consolidation, deterioration and crushing. The experimental investigations carried out allow creating a general picture of scatter of granules on sizes in each section and on length of device. On the basis of theoretical solution of Fokker-Planck equation the evolution of the distribution function of granules on sizes (Eqn. 12) and (Eqn. 14) has been obtained. In Figure 5 the comparison of experimental and theoretical curves of granules distribution yielding satisfactory conformity of experimental and calculated curves has been made. The value of the average granules size on length of drum device has been estimated. The curves of distribution yield full interpretation of a picture of quantitative change of granule sizes in each section on length of device which is very important factor at projecting of similar devices. A number of deformations of granules (Eqn. 18) have been proposed, on value of which one can judge about degree of deformation of granules.
It is noted that granules growth except other parameters, first of all has been connected with lamination thickness on surface of granule, depending on many factors, in most cases, not moving to the practical analysis and measurement. A solution of reverse incorrect problem on experimental values of average granule size allows estimating lamination thickness.
Glossary
a − diameter of granule;
dk − stochastic diffusion coefficient;
dk− diameter of drops of binding agent;
FN − normal force;
FA − adhesion force;
Fτ − tangential force;
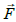 − resultant force vectors;
− resultant force vectors;
K − crushing coefficient;
L − length of apparatus;
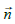 − unit normal vector;
− unit normal vector;
Pw − weight strength;
P(a) − probability function of granules distribution;
R − radius of drum apparatus;
Rp − average radius of pores of granules;
Sp − friction surface;
Sg − granule surface area;
t − stay time;
Vc − average displacement rate of granule in the device;
Δ − granule strength;
ε − porosity of granules;
εR − specific energy of dissipation;
λ − lamination thickness of powder;
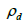 − density of hard phase;
− density of hard phase;
σD − density of liquid;
σD− deforming stress;
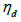 − dynamic viscosity of liquid;
− dynamic viscosity of liquid;
τw − destruction energy;
τp − penetration time;
ω − angular rate of rotation of drum;
Mo − Morton number;
Std − Stokes deformation number.
References
- Salman A, Hounslow M, Seville JPK (2006) Granulation. (1st edn), In: Handbook of Powdered Technology, Elsevier Ltd, UK, pp1402.
- Knight PC (2001) Structuring agglomerated products for improved performance. Powder Technol, USA pp 212-221.
- Bouwman AM (2005) Form, formation and deformation: the influence of material properties and process conditions of the shape of granules by high shear granulation. s.n.
- Keirens D (2000) Granulation, analysis of size distribution and porosity during consolidation in a batch drum granulator. The University of Queensland, Individual Inquiry, Australia.
- Ivensen SM, Listen JD (1998) Liquid-bound granule impact deformation and coefficient of restitution. Powder Technol 99: 234-242.
- Ceylan K, Kelbaliyev G (2001) Stochastic modeling of the granule size distribution in the agglomeration processes of powdered materials. Powder Technol 119: 173-180.
- Kelbaliev GI, Mamedov MI, Guseinov AS (1986) Determinative-stochastic modeling of the granulation of powdered materials. Theor Found Chem 20: 514-520.
- Levich VG (1962) Physical-chemical hydrodynamics. Englewood Cliffs, N.J., Prentice-Hall, USA.
- Peri J (1969) Handbook of engineer-chemist. L.: Khimiya 1: 639.
- Sarimeseli A, Kelbaliyev G (2004) Modeling of the break-up of deformable particles in turbulent flow. Chem Eng Sci 59: 1233-1242.
- Sis H, Kelbaliyev G, Chander S (2005) Kinetics of drop breakage in stirred vessels under turbulent conditions. J Dispersion Sci Technol 26: 565-573.
- Kelbaliev GI, Ibragimov ZI (2009) Coalescence and crushing of drops in isotrope turbulent flow. Teoret Osn Khim Tekhn, 3: 16-22.
- Kibbe AH (2000) Lactose. In:Handbook of Pharmaceutical Excipients. DC: American Pharmaceutical Association, 278 p.
- Kelbaliyev GI, Samedli VM, Samedov MM (2009) Modeling of granule process of powdered materials by method rolling. Powder Technol 194: 87-94.
- Klassen PP, Grishaev IT (1988) Bases of technique of granulation. М. p.272.
- Abberger T, Seo A, Shaefer T (2002) The effect of droplet size and powdered particle size on the mechanisms of nucleation and growth in liquid bed melt agglomeration. Int Jour Pharm 249: 185-197.
- Hapgood KP, Lister J, Smith R (2003) Nucleation regime map for liquid bound granules. AIChE J 49: 350-361.
- Kelbaliev GI (1992) Dislocation mechanism of consolidation of elastically connected particles in the process of granulation of powdered materials. Teor Osn Khim Tekhn 26: 749-754.
- Rhodes M (2008) Introduction on of particle Technology (2nd edn), John Wiley & Sons, Ltd, USA.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi