Research Article, Adv Biomed Res Innov Vol: 1 Issue: 1
Topological Defect Driven Membrane Fission
Mesarec L1, IgliÄ A1 and Kralj S2,3*
1Faculty of Electrical Engineering, Laboratory of Biophysics,University of Ljubljana, Tržaška, Slovenia
2Faculty of Natural Sciences and Mathematics, University of Maribor, Koroška, Slovenia
3Department of Condensed Matter Physics, Jožef Stefan Institute, Jamova, Slovenia
*Corresponding Author : Samo Kralj
Faculty of Natural Sciences and Mathematics, University of Maribor, Koroska, Slovenia
Tel: +386 31389278
E-mail: samo.kralj@um.si
Received: January 30, 2018 Accepted: February 27, 2018 Published: March 05, 2018
Citation: Mesarec L, IgliÄ A, Kralj S (2018) Topological Defect Driven Membrane Fission. Adv Biomed Res Innov 1:1.
Abstract
We demonstrated topological-defect driven membrane fission mechanism using a simple phenomenological model. We modeled membranes as effectively two-dimensional systems possessing in-plane ordering. Membrane configurations were described in terms of tensor orientational order parameter and curvature tensor. For demonstrative purpose we considered only membranes exhibiting spherical topology with axial and inversion symmetry. Using Effective Topological Charge Cancellation mechanism we showed that topological defects tend to assemble in regions exhibiting relatively strong Gaussian curvature. In particular, necklike membrane parts exhibit negative Gaussian curvature, which attract topological defects bearing negative topological charge. In geometries of our interest these defects can be formed via {defect, antidefect} depinning mechanism. The assembled defects, localized near the neck, give rise to relatively strong fluctuations at microscopic level, promoting membrane fission.
Keywords: Biological membranes; Membrane fission; Topological defects; Curvature
Introduction
Biological membranes [1,2] present an essential constituent of living cells. Their main role is to separate the interior of a cell from its surrounding, allowing selective transfer of specific materials through it. Configurational changes in membranes are in general correlated with important biological processes. In most cases membranes are composed of lipid bilayers, forming different lyotropic liquid crystal structures. Membranes often display some kind of in-plane orientational ordering, which could occur due to anisotropic shape of basic membrane components. Orientational ordering might be also a consequence of attached or embedded anisotropic proteins or lipids [2]. Despite their complexity, several key features of membranes and their functionality could be inferred by studying relatively simple models. Minimal models treat membranes as effectively two-dimensional (2D) systems [1-5]. Namely, their thickness is in general negligible small with respect to system’s characteristic linear dimension in other directions. If a membrane possesses some kind of in-plane ordering, it might exhibit topological defects (TDs) [6,7]. The latter correspond to localized distortions in a relevant order parameter field and they cannot be removed by local continuous transformations. At their origin of TDs, the ordering field is melted. Presence of TDs might have a dramatic impact on systems properties. For example, TDs might present nucleating sites for anomalous membrane structural growth [8,9].
In this contribution, we show that for appropriate conditions, TDs might enable fission of a membrane exhibiting in-plane ordering. To demonstrate this phenomenon, we use a simple mesoscopic minimal model, where we consider biological membranes possessing in-plane nematic-like ordering. Analogous systems represent nematic liquid crystalline shells in which configurations of TDs have been recently intensively studied due to their great potential for various future photonic applications [10-14]. The plan of the paper is as follows. In Sec. II we present theoretical background. Our minimal model is introduced in Sec. III. In Sec. IV we present defect-driven fission and in the last section we summarize the results of our study.
Theoretical background
Topological defects (TDs) represent points or lines where a relevant ordering field (which is in general introduced to describe configurations for relatively weak elastic distortions) exhibits singular behaviour [6,7]. TDs are characterised by a discrete topological charge, which is a conserved quantity. In 2D, the topological charge equals the winding number m [15]. It determines the number of reorientations of the ordering field along a line encircling the defect’s centre [15]. For a nematic director field, which exhibits the head-to-tail invariance, it holds m∈{±1/ 2, ±1, ±3 / 2…} . Assembling tendencies of TDs on surfaces exhibiting spatially nonhomogeneous Gaussian curvature K can be well predicted by the Effective Topological Charge Cancellation (ETCC) mechanism [16]. One characterizes each surface patch Δζ by its average characteristic Gaussian curvature
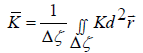 (1)
(1)
To each patch, we assign the effective topological charge [16]:
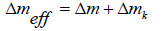 (2)
(2)
It consists of the topological charge Δm of “real” TDs and the spread curvature topological charge [17,18], which is defined as
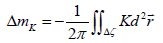 (3)
(3)
Therefore, 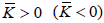 refers to a negative (positive) spread curvature topological charge. The ETCC mechanism claims [16] that in each surface patch, there is a neutralization tendency to cancel
refers to a negative (positive) spread curvature topological charge. The ETCC mechanism claims [16] that in each surface patch, there is a neutralization tendency to cancel 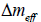 . Surface patches exhibiting
. Surface patches exhibiting 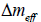 = 0 are claimed to be topologically neutral. In general it could hold that
= 0 are claimed to be topologically neutral. In general it could hold that 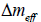 ≠ 0. In such cases, topological neutrality could be achieved either by redistribution of the existing TDs or via the creation of pairs {defect, antidefect}.
≠ 0. In such cases, topological neutrality could be achieved either by redistribution of the existing TDs or via the creation of pairs {defect, antidefect}.
Model
We consider 2D films exhibiting in-plane ordering. We set that orientational ordering is due to rod-like molecules constituting the film. We assume that rod-like molecules lie in the local tangent plane of a curved surface. Their local average mesoscopic orientation is determined by the so called [7] nematic director field 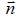 , where
, where 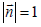 . The director field exhibits head-to-tail invariance (states ±
. The director field exhibits head-to-tail invariance (states ±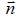 are physically equivalent). Such configurations can be represented by the tensor order parameter [14,19]
are physically equivalent). Such configurations can be represented by the tensor order parameter [14,19]
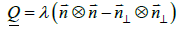 (4)
(4)
The amplitude λ ∈[−1/ 2,1 / 2] quantifies the degree of orientational ordering. Therefore, the absence of ordering corresponds to λ = 0 . Curvature of a local surface patch, characterised by the surface normal 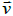 , is determined by the curvature tensor [14,19].
, is determined by the curvature tensor [14,19].
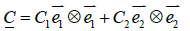 (5)
(5)
The unit vectors 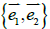 point along the surface principal directions exhibiting principal curvatures
point along the surface principal directions exhibiting principal curvatures 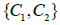 . Note that the Gaussian curvature K = C1C2 and the mean curvature
. Note that the Gaussian curvature K = C1C2 and the mean curvature 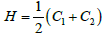 are invariants of
are invariants of 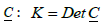 and
and 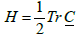 . Here Det and
. Here Det and 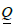 label the determinant and trace mathematical operation. Using invariants formed by
label the determinant and trace mathematical operation. Using invariants formed by 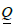 and
and 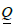 , we express the free energy density
, we express the free energy density 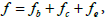 where we take into account only the most important contributions. Quantities
where we take into account only the most important contributions. Quantities 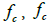 and fe stand for the membrane bending, condensation and elastic term, respectively. They are expressed as [1,14,16,19].
and fe stand for the membrane bending, condensation and elastic term, respectively. They are expressed as [1,14,16,19].
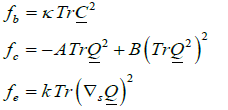 (6 a,b,c)
(6 a,b,c)
Here 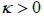 is a representative membrane bending constant favouring flat geometry. In the nematic phase, A and B are positive material constants, the elastic term is weighted with the positive elastic constant
is a representative membrane bending constant favouring flat geometry. In the nematic phase, A and B are positive material constants, the elastic term is weighted with the positive elastic constant 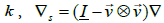 stands for the surface gradient operator and ∇ labels the 3D gradient operator [14,19]. Key material dependent length is given by the nematic order correlation length, which can be expressed as [14].
stands for the surface gradient operator and ∇ labels the 3D gradient operator [14,19]. Key material dependent length is given by the nematic order correlation length, which can be expressed as [14].
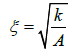 (7)
(7)
In simulations, we restrict to axial symmetric shapes exhibiting inversion symmetry. The shapes are in the Cartesian coordinates described using the parameterization [16].
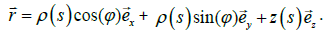 (8)
(8)
Here ρ and Z are variational parameters, s stands for the line element length and Õ ∈[0, 2π ] . We determine the configuration of a membrane by minimizing the total free energy for a fixed membrane surface and volume. Numerical details are described in [16].
Results
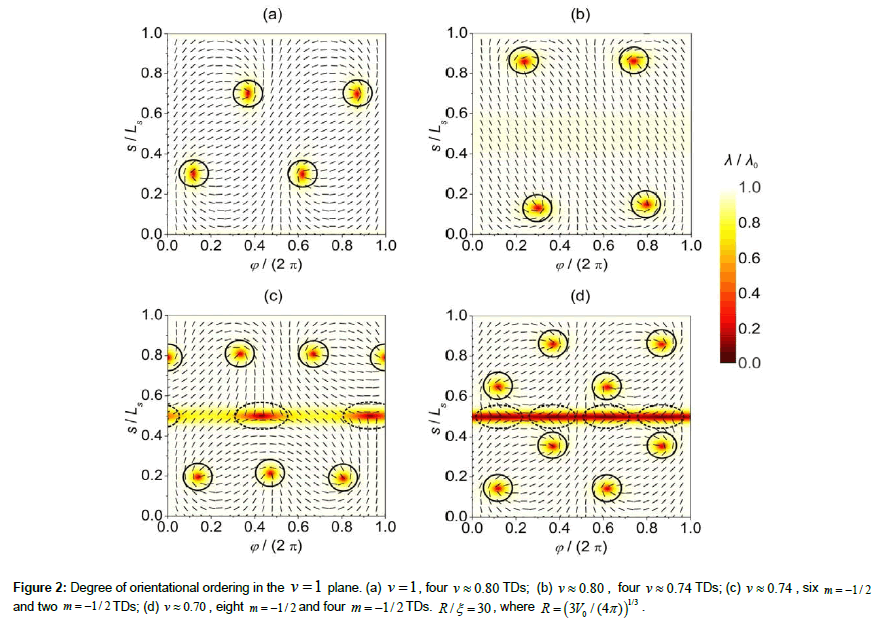
Below we demonstrate key stages of defect-driven membrane fission. We consider a membrane exhibiting spherical topology, possessing nematic in-plane ordering. Let us assume that it undergoes a shape transformation from a spherical-like shape to dumbbell-like shapes, which are shown in Figure 1b, 1c, 1d. In simulations, we enable this transformation by varying the relative volume 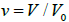 . Here, V stands for the membrane’s volume, and V0 represents the volume of a spherical membrane of the same surface area. In a perfect sphere, the structure possesses four TDs, which reside in the vertices of a hypothetical embedded tetrahedron (Figure 1a) [10]. In Figure 2, structures are shown in the (Õ, s) plane where TDs are clearly visible. Namely, centres of defect cores are melted (λ = 0) in order to avoid singularity in the elastic free energy penalty. In a sphere, the Gaussian curvature is spatially homogeneous and relative positions of TDs are dictated by repulsive interactions among TDs. A tetrahedron-type configuration maximizes their mutual separation.
. Here, V stands for the membrane’s volume, and V0 represents the volume of a spherical membrane of the same surface area. In a perfect sphere, the structure possesses four TDs, which reside in the vertices of a hypothetical embedded tetrahedron (Figure 1a) [10]. In Figure 2, structures are shown in the (Õ, s) plane where TDs are clearly visible. Namely, centres of defect cores are melted (λ = 0) in order to avoid singularity in the elastic free energy penalty. In a sphere, the Gaussian curvature is spatially homogeneous and relative positions of TDs are dictated by repulsive interactions among TDs. A tetrahedron-type configuration maximizes their mutual separation.
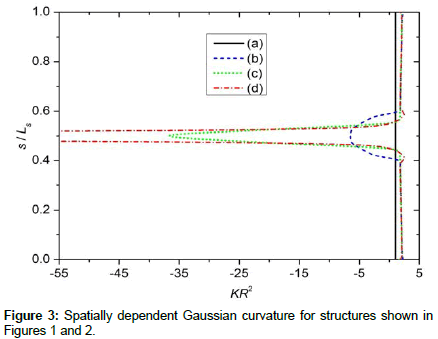
Figure 1: (a) Orientational order on a spherical membrane exhibits four m = 1/ 2 TDs due to topological requirements. From the perspective of ETCC mechanism, this structure is topologically neutral. Namely, the structure consists of only one curvature patch, within which the Gaussian curvature charge and the real charge exactly cancel each other. (b) Topologically charged dumbbell structure with four TDs. (c) Topologically charged dumbbell structure with eight TDs. (d) Topologically neutral dumbbell structures with twelve TDs. Ls represents the total length of the shape profile curve. The corresponding ordering is depicted in the (Õ, s) plane in Figures 2.
On decreasing K, a dumbbell shape begins to form. The Gaussian curvature becomes spatially dependent; see Figure 3, giving rise to spatial redistribution of TDs. In the 1st stage, shown in Fig. 1b and Fig. 2b, the TDs bearing positive topological charges begin to assemble at the spherical parts of the membrane. Within the neck of the structure, a region possessing negative K appears (Figure 3). The resulting structure can be viewed as consisting of three distinct surface patches. We label them as 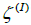 and
and 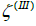 (spherical parts of the structure in Figure 1b, c, d) and
(spherical parts of the structure in Figure 1b, c, d) and 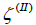 (the catenoid-like part of the structure in Figure 1b, 1c, 1d), characterised by
(the catenoid-like part of the structure in Figure 1b, 1c, 1d), characterised by 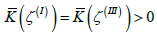 and
and 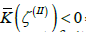 respectively (Figure 3). If four m = 1/ 2 TDs are present, finite effective topological charges appear in all three patches on decreasing v . For a pronounced dumbbell shape (consisting of two spheres connected by a thin neck) it roughly holds
respectively (Figure 3). If four m = 1/ 2 TDs are present, finite effective topological charges appear in all three patches on decreasing v . For a pronounced dumbbell shape (consisting of two spheres connected by a thin neck) it roughly holds 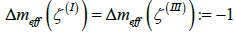 and
and 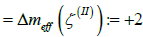 . In order to neutralize these patches, one needs to introduce TDs of total topological charge Δm =1 in the patches
. In order to neutralize these patches, one needs to introduce TDs of total topological charge Δm =1 in the patches 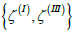 , and TDs of total topological charge Δm = −2 in
, and TDs of total topological charge Δm = −2 in 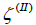 . This could be realized by depinning of four pairs {defect, antidefect} ={m =1/ 2,m = −1/ 2} . However, to form a pair, a large enough concentration of local elastic free energy is required, which should be comparable to the condensation penalty of forming the pair. Namely, the cores of TDs are essentially melted in order to avoid singularity in orientational ordering [16]. On decreasing v , this condition could be realised as it is demonstrated in Figure 1c. In the presented example, two pairs are formed, which reduces the effective topological charge in each surface patch. However, the resulting structure is still topologically charged. On further decreasing v , additional pairs could be formed giving rise to topological neutrality in all patches, which is shown in Figure 1d and 2d. In this case, maximal possible number of TDs is formed for geometries shown. Note that within our model, the free energy of the last structure is metastable with respect to the structure possessing eight TDs (i.e. six m = −1/ 2 and two m = −1/ 2 TDs). In simulations we stabilised it by enforcing 12 TDs (i.e. eight m =1/ 2 and four m = −1/ 2 m = −1/ 2 TDs) in the initial »seed« configuration. However, the main feature which we aim to emphasize is assembling of m = −1/ 2 antidefects within the neck. Their presence is accompanied by strong local fluctuations in orientational ordering on microscopic scale. The latter is manifested on mesoscopic scale by relatively weak degree of nematic ordering (i.e. essentially melted cores of TDs). Consequently, local interactions between nearby molecules are effectively weakened, which might result in the neck rupture. In such a way, two distinct membranes are formed, whose total free energy is lower than that of the structure shown in Figure 1c or 1d. This mechanism represents a possible membrane fission realization.
. This could be realized by depinning of four pairs {defect, antidefect} ={m =1/ 2,m = −1/ 2} . However, to form a pair, a large enough concentration of local elastic free energy is required, which should be comparable to the condensation penalty of forming the pair. Namely, the cores of TDs are essentially melted in order to avoid singularity in orientational ordering [16]. On decreasing v , this condition could be realised as it is demonstrated in Figure 1c. In the presented example, two pairs are formed, which reduces the effective topological charge in each surface patch. However, the resulting structure is still topologically charged. On further decreasing v , additional pairs could be formed giving rise to topological neutrality in all patches, which is shown in Figure 1d and 2d. In this case, maximal possible number of TDs is formed for geometries shown. Note that within our model, the free energy of the last structure is metastable with respect to the structure possessing eight TDs (i.e. six m = −1/ 2 and two m = −1/ 2 TDs). In simulations we stabilised it by enforcing 12 TDs (i.e. eight m =1/ 2 and four m = −1/ 2 m = −1/ 2 TDs) in the initial »seed« configuration. However, the main feature which we aim to emphasize is assembling of m = −1/ 2 antidefects within the neck. Their presence is accompanied by strong local fluctuations in orientational ordering on microscopic scale. The latter is manifested on mesoscopic scale by relatively weak degree of nematic ordering (i.e. essentially melted cores of TDs). Consequently, local interactions between nearby molecules are effectively weakened, which might result in the neck rupture. In such a way, two distinct membranes are formed, whose total free energy is lower than that of the structure shown in Figure 1c or 1d. This mechanism represents a possible membrane fission realization.
Conclusions
We demonstrated a possible topological defect driven mechanism of membrane fission in simple biological membranes exhibiting spherical topology and in-plane ordering. We showed that regions possessing negative Gaussian curvature could trigger the formation of pairs {defect, antidefect} and those antidefects assemble within the catenoid-like neck region. Presence of TDs is associated with relatively strong local fluctuations in orientational ordering. These weaken effective local intermolecular interactions which could enable rupture of the membrane into two independent objects.
In our study, we took into account only the so called intrinsic curvature terms in the free energy expression [20]. Such approach is used in the majority of theoretical studies, which are based on covariant derivatives in expressing free energy elastic terms [3,17,18]. However, groups lead by Selinger and Napoli demonstrated that extrinsic curvatures terms are in general also present [21-23]. They are present if local principal curvatures 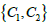 differ. The importance of this contribution increases with the difference
differ. The importance of this contribution increases with the difference 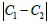 . In general, the extrinsic term favours orientational ordering along the principal direction exhibiting smaller curvature. In our case, its contribution would be largest within the neck region. Note that the impact of
. In general, the extrinsic term favours orientational ordering along the principal direction exhibiting smaller curvature. In our case, its contribution would be largest within the neck region. Note that the impact of 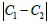 on neck structures was already studied within the so-called deviatoric elasticity model [5,24]. The latter considers membranes consisting of anisotropic constituents. These studies reveal that within the neck, the orientational ordering is increased. Therefore, this implies that TDs would assemble just above the neck, which does not change the qualitative picture of the proposed mechanism.
on neck structures was already studied within the so-called deviatoric elasticity model [5,24]. The latter considers membranes consisting of anisotropic constituents. These studies reveal that within the neck, the orientational ordering is increased. Therefore, this implies that TDs would assemble just above the neck, which does not change the qualitative picture of the proposed mechanism.
References
- Helfrich W (1973) Elastic properties of lipid bilayers: theory and possible experiments. Zeitschrift für Naturforschung C 28: 693-703.
- IgliÄ A, Drobne D, Kralj-IgliÄ V (2015) Nanostructures in biological systems: theory and applications. CRC Press.
- MacKintosh FC, Lubensky TC (1991) Orientational order, topology, and vesicle shapes. Phys Rev Lett 67: 1169.
- IgliÄ A, Babnik B, Gimsa U, Kralj-IgliÄ V (2006) On the role of membrane anisotropy in the beading transition of undulated tubular membrane structures. J Phys A: Math Gen 38: 8527.
- Kralj-IgliÄ V, Babnik B, Gauger D, May S, IgliÄ A, et al. (2006) Quadrupolar ordering of phospholipid molecules in narrow necks of phospholipid vesicles. J Stat Phys 125: 727-752.
- Mermin ND (1979) The topological theory of defects in ordered media. Rev Mod Phys 51: 591.
- Kurik MV, Lavrentovich OD (1988) Defects in liquid crystals: homotopy theory and experimental studies. Physics-Uspekhi 31: 196-224.
- Jesenek D, Perutkova Š, Kralj-IgliÄ V, Kralj S, IgliÄ A, et al. (2012) Exocytotic fusion pore stability and topological defects in the membrane with orientational degree of ordering. Cell Calcium 52: 277-282.
- Jesenek D, Petutkova Š, Góźdź W, Kralj-IgliÄ V, IgliÄ A, et al. (2013) Vesiculation of biological membrane driven by curvature induced frustrations in membrane orientational ordering. Int J Nanomed 8: 677-687.
- Vitelli V, Nelson DR (2006) Nematic textures in spherical shells. Phys Rev E 74: 021711.
- SeÄ D, Lopez-Leon T, Nobili M, Blanc C, Fernandez-Nieves A, et al. (2012) Defect trajectories in nematic shells: Role of elastic anisotropy and thickness heterogeneity. Phys Rev E 86: 020705.
- SkaÄÂej G, Zannoni C (2008) Controlling surface defect valence in colloids. Phys Rev Lett 100: 197802.
- Nelson DR (2002) Toward a tetravalent chemistry of colloids. Nano Lett 2: 1125-1129.
- Kralj S, Rosso R, Virga EG (2011) Curvature control of valence on nematic shells. Soft Matter 7: 670-683.
- Lavrentovich OD (1998) Topological defects in dispersed words and worlds around liquid crystals, or liquid crystal drops. Liq Cryst 24: 117-126.
- Mesarec L, Gozdz W, Iglic A, Kralj S (2016) Effective topological charge cancelation mechanism. Sci Rep 6: 27117.
- Vitelli V, Turner AM (2004) Anomalous coupling between topological defects and curvature. Phys Rev Lett 93: 215301.
- Bowick M, Nelson DR, Travesset A (2004) Curvature-induced defect unbinding in toroidal geometries. Phys Rev E 69: 041102.
- Rosso R, Virga EG, Kralj S (2012) Parallel transport and defects on nematic shells. Continuum Mech Thermodyn 24: 643-664.
- Kamien RD (2002) The geometry of soft materials: a primer. Rev Mod Phys 74: 953.
- Selinger RLB, Konya A, Travesset A, Selinger JV (2011) Monte Carlo studies of the XY model on two-dimensional curved surfaces. J Phys Chem B 115: 13989.
- Napoli G, Vergori L (2012) Surface free energies for nematic shells. Phys Rev E 85: 061701.
- Napoli G, Vergori L (2012) Extrinsic curvature effects on nematic shells. Phys Rev Lett 108: 207803.
- Iglic A, Babnik B, Bohinc K, Fosnaric M, Hagerstrand H, et. al. (2007) On the role of anisotropy of membrane constituents in formation of a membrane neck during budding of a multicomponent membrane. J Biomech 40: 579-585.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi 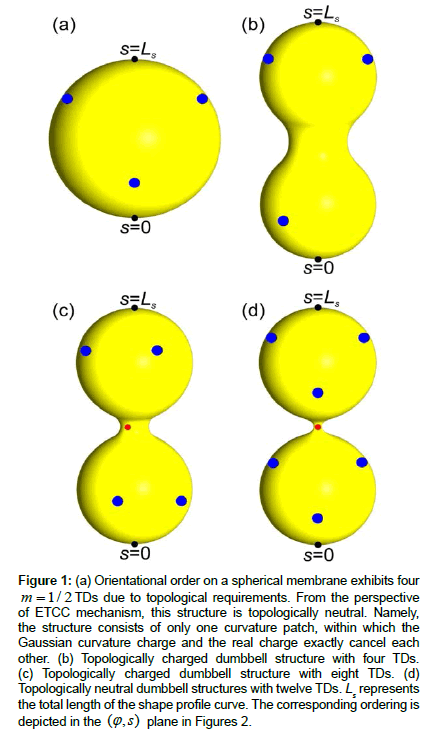
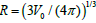 .
.