Short Communication, J Fashion Technol Textile Eng S Vol: 0 Issue: 1
A Multicriteria Decision Approach on Physical Properties of Socks Made from Different Fiber Types
Sena Cimilli Duru*, Cevza Candan and Banu Uygun Nergis
Department of Textile Engineering, Istanbul Technical University, Istanbul, Turkey
Corresponding author : Sena Cimilli Duru
Textile Technology & Design Faculty, Department of Textile Engineering, Istanbul Technical University, ITU Gumussuyu Yerleskesi Inonu Cad. No: 65 Oda:509, 34437 Taksim Istanbul, Turkey
Tel: +90 212 293 13 00/ 2774; Fax: +90 212 251 88 29
E-mail: cimilli@itu.edu.tr
Received: January 05, 2015 Accepted: August 15, 2015 Published: August 20, 2015
Citation: Duru SC, Candan C, Nergis BU (2015) A Multicriteria Decision Approach on Physical Properties of Socks Made from Different Fiber Types. J Fashion Technol Textile Eng S1:009. doi:10.4172/2329-9568.S1-009
Abstract
The aim of the study is to investigate the physical properties of sock fabrics made from some new regenerated fibers such as modal, micro modal, bamboo, soybean and chitosan. Also, samples from cotton and viscose fibers were produced in the study for comparison reasons. The results obtained seemed that the new regenerated fibers, especially the soybean fiber may still be preferred for socks, as they have high abrasion resistance as well as bursting strength, which is important for a garment’s life time, in addition to their natural antibacterial property. Also, it was shown that TOPSIS can be a beneficial tool for this kind of researches. By using TOPSIS, a single ranking taking into account preferences of the decision-maker and priorities arranged according to the final goal can be obtained. The data obtained showed that fabrics made from soybean fiber were the best alternative from among all.
Keywords: Sock; Comfort; New regenerated fibers; Multicriteria decision making
Introduction
Generally, fabrics having different physical properties were ranked according to properties using different statistical analysis methods. However, better results about the desired end-product properties are obtained if the priorities and preferences of the decision-maker namely the textile engineer is taken into consideration and multicriteria decision making methods (MCDM) are useful means for carrying out such an analysis. There are some studies related to applying MCDM to textile problems. Majumbar et al. [1] developed an algorithm which works by amalgamating TOPSIS and genetic algorithm to determine the quality value of cotton fiber considering two yarn properties namely yarn tenacity and unevenness. In another paper of Majumbar et al. [2], AHP and TOPSIS methods were used to develop software for cotton fiber grading and selection. Also a fuzzy AHP model has been developed to solve the raw material selection problem of the textile spinning industry [3]. Moghassem and Bahramzadeh [4] tested the applicability of the TOPSIS approach in obtaining optimum spinning conditions for rotor spun yarn that is intended to be used in a weft knitting machine. According to the final ranking, the spinning condition in which the sample was spun by using a spiral nozzle, a doffing tube without a torque stop, and a closer setting had the highest closeness coefficient to the ideal solution. Appropriate components of the doffing tube and its adjustment for rotor spun yarn intended to be used for weft knitted fabrics were selected by extended version of the TOPSIS. In order to select the appropriate setting in rotor spinning machine for Ne 30 rotor yarn intended to be used for weft knitted fabric, TOPSIS method was used by Moghassem and Fallahpor [5]. Fuzzy TOPSIS method for group decision making was proposed for the alternatives selection in yarn tension detection and control system by Minna and Yan [6]. In the study conducted by Majumbar et al. [7] selection of navel rotor spinning machine, which influences various quality parameters of the final yarn was investigated by combining TOPSIS and AHP methods. Relative importance of the yarn quality parameters was evaluated by using AHP method, keeping in mind the requirements of denim fabric. The final ranking of navels was elicited in accordance with the relative closeness value determined by TOPSIS method. Kaplan, Araz, and Goktepe [8] applied ELECTRE outranking method for the selection of rotor navel. Mitra et al. [9] attempted to develop a simple index of handloom fabric quality, which can be used for selecting fabrics for a specified end use. AHP and MAHP multi-criteria decision making (MCDM) were used for ranking 25 handloom cotton fabrics in terms of their overall quality value considering their applicability as summer clothing materials. Under the different conditions of temperature and humidity, moisture absorption, water transmissibility, water retention and moisture liberation of stitch-bonded fabrics with different content of hemp was tested by Hao et al. [10]. According to multiple properties of the moisture absorption and quick drying, the tested performance of five aspects were used to build the evaluation system and TOPSIS method was employed to establish a comprehensive evaluation method. Duru and Candan [11] applied hybrid AHP and TOPSIS methods in order to select best option in terms of wicking and drying characteristics of seamless garments. Hong and Su [12] employed a hybrid of the Taguchi and TOPSIS methods to determine the optimal processing parameter combination for PET/TiO2 UV-resistant fiber melt-spinning using a minimum number of experiments. Dulange et al. [13] identified the critical success factors influencing the performance of power loom textiles, to evaluate their impact on the organizational performance and to find out the effect of these factors on the organizational performance of small and mediumsized enterprises (SMEs) in the Solapur (Maharashtra) industrial sector using AHP. For supply chain selection and organization, there are also some studies to select the best alternative for all among all. Yücel and Güneri [14] developed a new model that complements the weakness and proposes a complete fuzzy multi-objective linear model approach for the supplier selection problem while Yayla et al. [15] used the fuzzy TOPSIS method to select the most appropriate supplier of garment ‘X’ operating in Turkey. Eleren and Yılmaz [16] developed and applied a TOPSIS model that could help managers to select most appropriate supplier within the textile sector in Usak. Tanyas [17] designed the performance evaluation system in a textile global sourcing office using Balanced Scorecard method with the help of AHP within a supply chain perspective.
During the daily life, owing to the fact that socks are connected with skin and shoes directly, they are subjected to more physical forces than other types of garments. As a result, they need to perform better physical characteristics than the others. With the help of literature survey, it was found that there is no published literature that focuses on physical properties of textile knitted fabrics, using TOPSIS or AHP method of MCDM. For this purpose, in this study, a multicriteria decision making method, TOPSIS and AHP methods, were used in order to select the sock fabric with best physical properties. New regenerated fibers such as modal, micro modal, bamboo, soybean and chitosan were selected for the study. Also, due to the limited number of studies about the performances of these fibers, in an intention to compare their properties with conventional ones, cotton and viscose were also edited to the study.
Materials and Methods
The details regarding the fiber types and yarns are given in Table 1. For the work, sock fabrics were knitted on a Nagata D210 double cylinder hosiery machine of 176 needles at the same knitting settings (i.e. the loop length for all sock samples was kept constant for each sample).
| Cotton | Modal | Viscose | Micro modal | Bamboo | Chitosan | Soybean | |
|---|---|---|---|---|---|---|---|
| Fiber fineness (dtex) | 1.5 | 1.2 | 1.59 | 0.82 | 1.57 | 0.93 | 1.91 |
| Fiber length (mm) | 28.1 | 40.8 | 38.1 | 35.3 | 36.2 | 37.6 | 41.1 |
| Yarn Count (Ne) | 29.1 | 28.9 | 30.2 | 29.0 | 29.4 | 30.4 | 29.2 |
| Yarn Twist Coefficient (αe) | 3.57 | 3.31 | 3.54 | 3.15 | 3.33 | 3.54 | 3.65 |
| Fiber cross-section* | 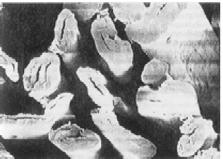 |
 |
 |
 |
 |
 |
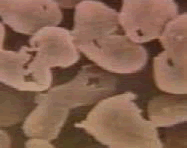 |
Table 1: Properties fibers and yarns.
Unlike ordinary sock fabrics, nylon and elastane were not utilized in the production of the plain jersey socks for the work in an attempt to investigate the effect of fiber type on physical properties of the samples. In addition to that, all sock samples were dyed and finished under the same conditions. Fabric weight, thickness, bursting strength, abrasion resistance, dimensional stability tests were done in accordance with TS 251, BS 2544, TS 393 EN ISO 13938-1, ASTM D4966, ISO 3759-BS4923 standards, respectively. The overall porosity is defined as the ratio of open space to the total volume of the porous material and accordingly it 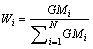 as calculated from the measured thickness and weight per unit area values using the following equations [18]:
as calculated from the measured thickness and weight per unit area values using the following equations [18]:
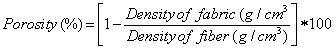 (1)
(1)
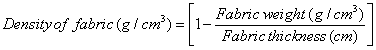 (2)
(2)
A decision making problem is the process of finding the best option from all of the feasible alternatives. Multi-criteria decision making may be considered as a complex and dynamic process that includes one managerial level and one engineering level. TOPSIS is a kind of multi-criteria method to identify solutions from a finite set of alternatives. The basic principle is that the chosen alternative should have the shortest distance from the positive ideal solution and the farthest distance from the negative ideal solution [2]. The AHP is a powerful and flexible multi-criteria decision making tool by structuring a complicated decision problem hierarchically at several different levels where both qualitative and quantitative aspects need to be considered [19]. The combination of AHP and TOPSIS can handle the choosing the best fiber type which gives feeling more comfortable. In the case of hybrid AHP-TOPSIS method the pair-wise comparison method of AHP is amalgamated with the other steps of TOPSIS and the procedure of the hybrid AHP-TOPSIS method can be expressed in a series of steps [20-22] given as follows:
Step 1: The relevant objective or goal, decision criteria and alternatives of the problem are identified in this step.
Step 2: A decision matrix of criteria and alternatives is formulated on the basis of information available regarding the problem. The number of alternatives is M and the number of criteria is N where an element aij of the decision matrix Dmxn represents the actual value of the ith alternative in terms of jth decision matrix.
Step 3: The decision matrix is converted to a normalized decision matrix. The normalized value rij is calculated as:
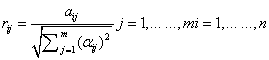 (3)
(3)
Step 4: The relative importance of different criteria with respect to the objective of the problem is determined using AHP. To do so, a pair-wise comparison matrix of criteria is constructed using a scale of relative importance. The judgements are entered using the fundamental scale of AHP, which is shown in Tables 2 and 3.
| Fiber type | Thickness (mm) | Weight (g/m2) | Stitch density (loops/cm2) | Porosity (%) | Regain (%) |
|---|---|---|---|---|---|
| Cotton | 0.93 | 195 | 95 | 86.1 | 23.8 |
| Modal | 0.75 | 182 | 98 | 84.0 | 22.2 |
| Viscose | 0.90 | 197 | 99 | 85.4 | 10.5 |
| Micro modal | 0.69 | 168 | 99 | 84.0 | 15.0 |
| Bamboo | 0.74 | 193 | 109 | 83.8 | 14.3 |
| Chitosan | 0.81 | 179 | 102 | 83.0 | 5.0 |
| Soybean | 0.74 | 167 | 104 | 82.5 | 10.0 |
Table 2: Properties fabric.
| Intensity of importance on a absolute scale | Definition | Explanation |
|---|---|---|
| 1 | Equal importance | Two activities contribute equally to the objective. |
| 3 | Moderate importance of one over another | Experience and judgement slightly favor one activity to another |
| 5 | Essential or strong importance | Experience and judgement strongly favor one activity to another |
| 7 | Very strongly importance | An activity is strongly favored and its dominance is demonstrated in practice |
| 9 | Extreme importance | The evidence favoring one activity over another is of the highest possible order of affirmation. |
Table 3: Nine point scale of relative importance [20-22].
For N criteria, the size of this comparison matrix will be NxN and the entry cijwill denote the comparative importance of criteria I with respect to criteria j. In the matrix cij=1 when i=j and cji=1/cij. The pair-wise comparison matrix (C1) of criteria is shown below:
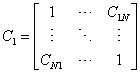
The normalized weight or importance of the ith criteria (Wi) is determined by calculating the geometric mean of the ith row (GMi) of the above matrix and then normalizing the geometric means of rows as:
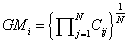 (4)
(4)
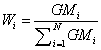 (5)
(5)
To check the consistency in pair-wise comparison judgment, consistency index (CI) and consistency ratio (CR) are calculated using the following equations where (λmax) is the maximum eigen value.
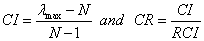 (6)
(6)
where RCI is random consistency index and its value can be obtained from Table 4. If the value of CR is 0.1 or less than the judgment is considered to be consistent and therefore acceptable. Otherwise, the decision maker has to be reconsidering the entries of pair wise comparison matrix.`
| M | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RCI | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
Table 4: RCI values for different numbers of alternatives (m) [20-22].
Step 5: The weighted normalized value υij is calculated as
υij = W × rijj = 1,… …, mi = 1,… … ,n (7)
where Wi is the weight of the ith attribute of criterion and 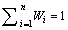
Step 6: The positive ideal and negative ideal solution are determined by following formulations:
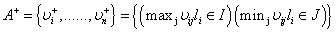 (8)
(8)
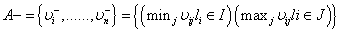 (9)
(9)
where I is associated with benefit criteria and J is associated with cost criteria.
Step 7: The separation measure using the n-dimensional Euclidean distance is calculated.
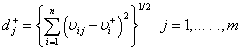 (10)
(10)
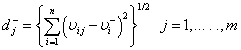 (11)
(11)
Step 8: The relative closeness to the ideal solution is determined.
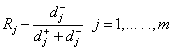 (12)
(12)
Since then clearly Rj ∈ [0,1]
Step 9: All the alternatives are arranged in a descending order according to value of Rj. The alternative at the top of the list is the most preferred one.
Results
The tested properties of the fabrics can be seen in Table 5.
| Weight loss (%) | Bursting strength (kg/cm2) | Widthwise shrinkage of the socks (%) | Lengthwise shrinkage of the socks (%) | |
|---|---|---|---|---|
| Cotton | 7.04 | 6.0 | -4.84 | -10.94 |
| Modal | 9.80 | 4.2 | 1.25 | -5.31 |
| Viscose | 5.14 | 4.8 | -0.16 | -14.69 |
| Micro modal | 19.00 | 4.8 | -2.97 | -8.75 |
| Bamboo | 6.88 | 3.8 | -7.50 | -10.31 |
| Chitosan | 5.21 | 4.7 | -4.06 | -6.72 |
| Soybean | 3.86 | 7.0 | -5.00 | -11.25 |
Table 5: Results of the tests.
For performing the TOPSIS evaluation; weight loss, bursting strength, width wise and lengthwise dimensional stability were taken as a weight. Analytic hierarchy process was used to determine the relative weights of four decision criteria according to their relative importance for fabric performance (Table 6). Here the comparisons were made according to the Saaty’s nine-point scale given in Table 3. The scores given in Table 6 represent the perception of the decision maker about the relative importance of the four fabric parameters. These scores can vary from one decision maker to another and also with the intended use of the fabrics. It can be said from Table 6 that weight loss and bursting strength are more dominant parameters than dimensional stabilities of the fabrics and the relative weights of both parameters were found to be maximum 0.375.
| Weight loss | Bursting strength | Widthwise DS | Lengthwise DS | |
|---|---|---|---|---|
| Weight loss | 1 | 1 | 3 | 3 |
| Bursting strength | 1 | 1 | 3 | 3 |
| Widthwise DS | 0.33 | 0.33 | 1 | 1 |
| Lengthwise DS | 0.33 | 0.33 | 1 | 1 |
Table 6: Pair-wise comparison matrix of criteria with respect to objective and codes.
Table 7 shows calculated weights and codes of the four criterias.
| Criteria | Code | Weights |
|---|---|---|
| Weight loss | C1 | 0.375 |
| Bursting strength | C2 | 0.375 |
| Widthwise DS | C3 | 0.125 |
| Lengthwise DS | C4 | 0.125 |
Table 7: The criteria weights.
For the measurement of consistency of judgment the original matrix is multiplied by the weight vector to get the product. By help of equation 6, λmax was found 4. Therefore; CI=0 and <0. As the value of CR is below 0.1 the comparison matrix remains consistent. Vector normalization was made and weighted normalized matrix was formed and then positive and negative ideal solutions were calculated (Table 8).
| C1 | C2 | C3 | C4 | |
|---|---|---|---|---|
| W=1 | 0.375 | 0.375 | 0.125 | 0.125 |
| Cotton | -0.1058 | 0.1653 | -0.0527 | -0.0510 |
| Modal | -0.1473 | 0.1157 | 0.0136 | -0.0248 |
| Viscose | -0.0773 | 0.1322 | -0.0017 | -0.0685 |
| Micro modal | -0.2856 | 0.1322 | -0.0324 | -0.0408 |
| Bamboo | -0.1034 | 0.1047 | -0.0817 | -0.0481 |
| Chitosan | -0.0783 | 0.1295 | -0.0442 | -0.0313 |
| Soybean | -0.0580 | 0.1929 | -0.0545 | -0.0525 |
| Positive ideal solution | -0.0580208 | 0.1928636 | 0.0136221 | -0.0247665 |
| Negative ideal solution | -0.2855948 | 0.1046974 | -0.0817327 | -0.0685161 |
Table 8: Weighted normalization matrix of fabrics.
After identifying positive (A+) and negative ideal solution (A-), the separation of each alternative from the ideal solution was calculated using equations 8 and 9. The relative closeness of the alternatives (Rj) to the ideal solution (Aj) was defined by the equation 12 with respect to A+. Based on the closeness of the coefficient to the ideal solution (Rj value), ranking of the preference order of all alternatives in descending order is shown in Table 9.
| Fabrics | d+ | d- | Relative closeness | Rank |
|---|---|---|---|---|
| Soybean | 0.0735 | 0.2461 | 0.77 | 1 |
| Viscose | 0.0787 | 0.2249 | 0.74 | 2 |
| Chitosan | 0.0884 | 0.2153 | 0.71 | 3 |
| Cotton | 0.0902 | 0.1927 | 0.68 | 4 |
| Modal | 0.1180 | 0.1739 | 0.60 | 5 |
| Bamboo | 0.1395 | 0.1833 | 0.57 | 6 |
| Micro modal | 0.2405 | 0.0630 | 0.21 | 7 |
Table 9: Preference order of alternatives.
For this study, weight loss and bursting strength parameters are more important than dimensional stability of the fabrics and so their weights are higher. As a result, fabrics made from soybean fiber performed the best alternative from all among others because of its lowest weight loss and highest bursting strength values. On the other hand, although fabrics made from micro modal ones were dimensional stable, its weight loss value was so high which made this very fabric the least preference one.
Conclusion
Weight loss, bursting strength, widthwise and lengthwise properties of the fabrics produced from new fibers such as micro modal, bamboo, soybean, and chitosan were knitted for the experimental work discussed in the paper. In the light of the data obtained, the fiber type seems to markedly affect the physical properties discussed. Moreover, both experimental results and TOPSIS evaluations showed that it was the soybean sock fabrics which performed relatively better than the other fabrics in terms of the mechanical properties where as micro modal fabrics were the worst ones.
References
- Majumdar A, Prakash S (2014) A New Approach to Determine the Quality Value of Cotton Fibres Using Multi-criteria Decision Making and Genetic Algorithm. Fibers and Polymers 15: 2658-2664.
- Majumbar A, Mangla R, Gupta A (2010) Developing a Desicion Support System Software for Cotton Fibre Grading and Selection. IJFTR 35: 195-200.
- Majumbar A (2010) Selection of Raw Materials in Textile Spinning Industry Using Fuzzy Multi-criteria Decision Making Approach. Fibers and Polymers 11:121-127.
- Moghassem AR, Bahramzadeh H (2010) Application of Multi-Criteria Analysis for Parameters Selection Problem in Rotor Spinning Machine. Text Res J 80: 2176-2187.
- Moghassem A, Fallahpour A (2011) Selecting Doffing Tube Components for Rotor-Spun Yarn for Weft Knitted Fabrics Using Multi-criteria Decision Making Approach with Interval Data. Journal of Engineered Fibers and Fabrics 6: 44-53.
- Minna N, Yan L (2013) Schemes Selection of Yarn Tension Detection and Control Based on Fuzzy Multiple Attribute Group Decision Making. International Conference on Mechanical and Automation Engineering 188-192.
- Majumbar A, Kaplan S, Göktepe Ö (2010) Navel Selection for Rotor Spinning Denim Fabrics Using a Multi-Criteria Decision-Making Process. J Text I 101: 304-309.
- Kaplan S, Araz C, Göktepe Ö (2006) A Multicriteria Decision Aid Approach on Navel Selection Problem for Rotor Spinning. Text Res J 76: 896-904
- Mitra A, Majumbar A, Ghosh A, Majumbar PK, Bannerjee D (2015) Selection of Handloom Fabrics for Summer Clothing Using Multi-Criteria Decision Making Techniques. Journal of Natural Fibers 12: 61-71.
- Hao X, Hao X, Zhang J, Li H, Zhang G, et al. (2013) Investigation and Evaluation on the Moisture-absorption and Quick-drying Properties of Stitch-bonded Nonwoven Fabrics with Hemp/Polyester Blended Used in Shoe’s Lining. Advanced Materials Research 602-604: 847-852
- Duru SC, Candan C (2013) Effect of repeated laundering on wicking and drying properties of fabrics of seamless garments. Text Resh J 83: 591-605.
- Hong GB, Su TL (2012) Statistical Analysis of Experimental Parameters in Characterization of Ultraviolet-Resistant Polyester Fiber Using a TOPSIS-Taguchi Method. Iran Polym J 21:877-885.
- Dulange SR, Pundir AK, Ganapathy L (2014) Prioritization of Factors Impacting on Performance of Power Looms Using AH.P J Ind Eng Int 10:217-227.
- Yucel A, Güneri AF (2011) A Weighted Additive Fuzzy Programming Approach for Multi-Criteria Supplier Selection. Expert Syst Appl 38: 6281-6286.
- Yayla AY, Özbek A, Yildiz A (2012) Fuzzy TOPSIS Method in Supplier Selection and Application in the Garment Industry. Fibres & Textiles in Eastern Europe 4: 20-23
- Eleren A, Yilmaz C (2011) Selection of Suppliers by Fuzzy Topsis Model; Sample Study from Turkey. International Journal of Business and Social Science 2: 189-200.
- Tanyas M, Candan C, Cesur K (2010) Supply Chain Management in Textile and Supplier Performance Evaluation. 10th Global Conference on Business & Economics, Rome, Italy.
- Cimilli S, Nergis B, Candan C, Ozdemir M (2010) A Comparative Study of Some Comfort Related Properties of Socks From Different Fiber Types. Text Res J 80: 948-957.
- Pöyhönen M, Hämäläinen R (2001) On the Convergence of Multiattribute Weighting Methods. Eur J Oper Res 129: 569-585.
- Moghassem AR, Bahramzadeh H (2010) Application of Multi-Criteria Analysis for Parameters Selection Problem in Rotor Spinning. Text Res J 80: 2176-2187.
- Majumbar A, Sarkar B, Majumbar PK (2005) Determination of Quality Value of Cotton Fibre Using Hybrid AHP-TOPSIS Method of Multi-Criteria Desicion-Making. J Text I 96: 303-309.
- Shyjith K, Ilangkumaran M, Kumanan S (2008) Multi-Criteria Desicion Making Approach to Evaluate Optimum Maintance Strategy in Textile Industry. Journal of Quality in Maintance Engineering 14: 375-386.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi