Research Article, J Appl Bioinforma Comput Biol Vol: 7 Issue: 2
Communities of Dense Weighted Networks
Mahashweta Basu*
Center for Bioinformatics and Computational Biology, University of Maryland, College Park, Maryland 20742, USA
*Corresponding Author : Mahashweta Basu
Center for Bioinformatics and Computational Biology, University of Maryland, College Park, Maryland 20742, USA
E-mail: mahashwetabasu@gmail.com
Received: December 11, 2017 Accepted: March 09, 2017 Published: January 11, 2018
Citation: Basu M (2018) Communities of Dense Weighted Networks. J Appl Bioinforma Comput Biol 7:2. doi: 10.4172/2329-9533.1000152
Abstract
Complex networks are intrinsically modular. Resolving small modules is particularly difficult when the network is densely connected; wide variation of link-weights invites additional complexities. In this article we present an algorithm to detect community structure in densely connected weighted networks. First, modularity of the network is calculated by erasing the links having weights smaller than a cutoff q. Then one takes all the disjoint components obtained at q=qm, where the modularity is maximum, and modularize the components individually using Newman Girvan’s algorithm for weighted networks. The performance of the proposed algorithm is evaluated on four different types of network. Initially taking microRNA (miRNA) co-target network of Homo sapiens as an example, we show that this algorithm could reveal miRNA modules which are known to be relevant in biological context. We also demonstrate the algorithm for scientific collaboration network, character interaction network of the novel Les Miserables, neural network of C. elegans and email communication network among employees of a company. In all these cases this new algorithm could efficiently detect all the relevant modules, particularly the small ones which are very strongly connected.
Keywords: Complex networks; Nodes; Modules; Edges
Introduction
Networks, a set of nodes or vertices joined pairwise by links or edges, are commonly used for describing socio-logical (scientific collaborations [1] and acquaintance net-works [2]), biological (proteins interactions, genes regulatory, food webs, neural networks, metabolic networks), technological (Internet and the web) and communication (airport [3], road [4,5], and railway network [6,7]) systems. The topological properties of these complex networks [8,9] help in identifying underlying community structures [10], network motifs [11], connectivity [12] and several other properties [13]. The links of a network can also be weighted. Some of the networks are associated with links of varying strengths [14-17] represented by linkweights. The topological properties of weighted networks [18,19] are quite different and their study requires additional care. In particular, when link-weights vary in a wide range, one need to identify suitably the irrelevant links and ignore them to simplify the network [20].
Most networks in nature, whether weighted or not, exhibit community (or modular) structures. Detection of communities in the complex networks provide invaluable information on the underlying synergism. Nodes which belong to a particular module are more than likely to function together for some common cause; being able to unravel such communities help in identifying functional properties of the network. For example, in social networks [21], communities observed are based on interests, age, profession of the people. Similarly, communities reflect the themes of the web-pages in World Wide Web, related papers on a single topic in citation networks [22], subsystems within ecosystems [23,24] in food webs, and it may relate to functional groups [25,26] in cellular and metabolic networks.
To reveal the community structure of complex networks several methods have been devised, which includes Kernighan-Lin algorithm [27], spectral partitioning [28,29], hierarchical clustering [30] etc. Some of the recent algorithms are based on centrality measures [10], percolation models [31], random walks [32,33], resistor networks [34] and many others [35-39]. Majority of these methods are, however, context based and rely on maximization of a quantity called modularity Q. For any given partition, Q quantifies [34] the links present within the modules minus the expected number of links of an equivalent random network. Based on the idea, that best partition of a network is the one with maximum Q, Newman and Girvan have developed a couple of algorithms [10,34,40] which are further extended to include large [41] and weighted [42] networks. Newman Girvan’s modularization (NGM) algorithms, though widely used for finding modules of both weighted and unweighted networks, have some shortcomings [43]. It was argued that modularity maximization algorithm can resolve the network upto a scale that depends on the total number of links l; a module having more than 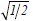 links cannot be resolved even when it is a clique and connected to external modules through just one link. Moreover, the situation gets worse when substantial number of small communities coexist with large ones. This observation is also true for weighted networks [44,45]. Therefore modularity maximization uncovers only large modules missing important sub-structures which are small.
links cannot be resolved even when it is a clique and connected to external modules through just one link. Moreover, the situation gets worse when substantial number of small communities coexist with large ones. This observation is also true for weighted networks [44,45]. Therefore modularity maximization uncovers only large modules missing important sub-structures which are small.
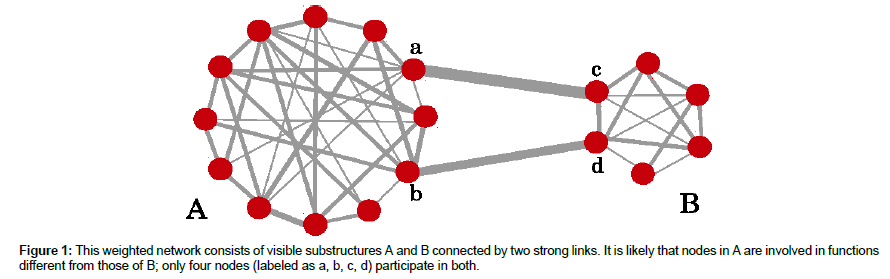
Weighted networks bring in additional difficulties. Here, modularity maximization methods prefer to assign the links with small weights as the inter-module links. For networks with wide weight distribution, however, it is difficult to identify the links which should be taken as inter-module connections. To overcome this difficulty a clustering method has been proposed recently by Mookherjee et al. [20] in context of microRNA co-target network of Homo sapiens which is a weighted network with dense connections. This algorithm also suffers from certain short comings. First, the method has certain in-built arbitrariness in determining the total number of clusters. In addition, its sub-structures connected by large-weighted links, if any, remains undetectable. This situation begets the confusion whether inspite of presence of visibly distinct sub-structure they should be considered as a single component or be treated as two separate modules (Figure 1). In certain biological contexts, a circumstance, may correspond to two modules which does independent functions, but only a few nodes are significantly involved in both functions (Figure 1). Thus it is important to consider these sub-structures as independent modules, even though it lowers the modularity; or otherwise each module will act as a noise for each other while identifying their functionality. Details of the algorithm and its shortcomings are discussed in the next section.
In this article we propose a new algorithm in an effort to overcome these shortcomings and to efficiently determine the communities of any dense weighted network. Initially we demonstrate the algorithm using the microRNA co-target network of Homo sapiens and compare the modules with those obtained by NGM algorithm for weighted networks [42] and the clustering algorithm [20]. Later we also successfully identify the modules of four other real world networkscollaboration network of scientific [34], interaction network between the characters of the novel Les Miserables [46,47], neural network of C. elegans, and email communication network [48] among the employees of a small company.
Clustering algorithm
In a recent article, Mookherjee et al. [20] has proposed an algorithm to find clusters of miRNA co-target network of Homo sapiens. MicroRNAs are short non-coding RNAs which usually suppress gene expression in post-transcriptional level [49]. Taking the predicted targets of 711 miRNAs of Homo sapiens from Microcosm Target database [50], the authors constructed the co-target network by joining miRNAs pairwise by weighted links. The link-weight w corresponds to the number of common targets of the concerned pair. The network thus constructed consists of 711 miRNAs (nodes) and 252405 edges. Since the network is fully connected, it is evident that clusters containing less than half the number of nodes cannot be resolved by standard algorithms [34,42]. To obtain the clusters of this densely packed network Mookherjee et al. [20] have adopted the following strategy.
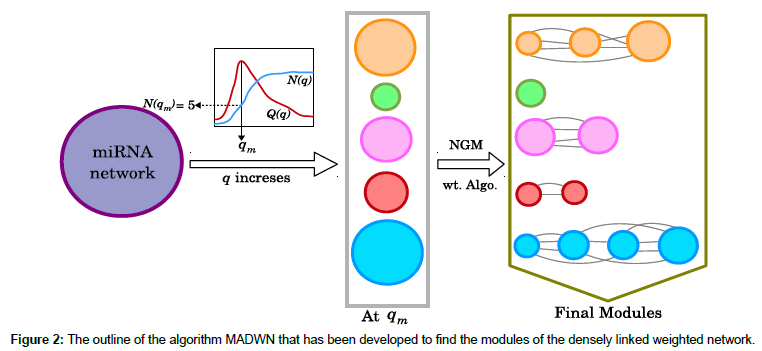
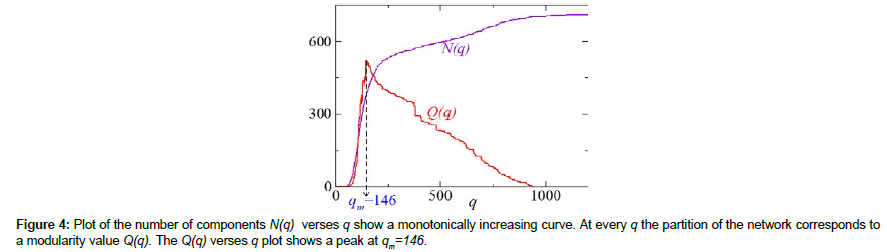
The link-weights of this network vary in a wide range: minimum being 1 and maximum 1253. Thus most links are considered irrelevant in determining the clusters. In an attempt to simplify the network, links with weights smaller than a pre-defined cutoff value q are erased; the resulting network breaks into small disjoint components. Denoting, N(q) as the number components the authors find that N(q) does not increase substantially until q reaches a threshold value q* and then it breaks quickly into large number of components (Figure 2) [20]. Thus the network is optimally connected at q*=103 where 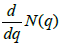 is maximum. Among all the components obtained at q*=103, the largest one
is maximum. Among all the components obtained at q*=103, the largest one 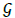 contains 479 miRNAs. A large fraction of miRNAs present in
contains 479 miRNAs. A large fraction of miRNAs present in 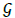 are found to down regulate expression of genes involved in several genetic diseases. To explore how miRNAs are organized in
are found to down regulate expression of genes involved in several genetic diseases. To explore how miRNAs are organized in 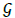 , q is increased further until the total number of components does not change much. At q=160, the subgraph
, q is increased further until the total number of components does not change much. At q=160, the subgraph 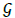 has 70 components (called miRNA clusters) and 149 lone miRNAs. Note that if we consider all 711 miRNAs, instead of 479 miRNAs belonging to
has 70 components (called miRNA clusters) and 149 lone miRNAs. Note that if we consider all 711 miRNAs, instead of 479 miRNAs belonging to 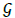 , the total number of clusters would have been 94 (Table 1-3).
, the total number of clusters would have been 94 (Table 1-3).
| Component Size : | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 12 | 16 | 47 | 85 |
| Frequency : | 284 | 47 | 24 | 8 | 6 | 5 | 1 | 1 | 1 | 1 | 1 |
Table 1: The distribution of size of the components at qm=146 for miRNA co-target network of Homo sapiens.
| Module size : | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 11 | 12 | 13 | 14 | 19 | 21 |
| Frequency : | 65 | 38 | 4 | 5 | 1 | 1 | 3 | 1 | 2 | 1 | 1 | 1 | 1 |
Table 2: Size distribution of miRNA modules obtained using MADWN. Note that there are 284 number of lone miRNAs which are not shown here.
| Methods | N(q) | Q(q) | Component size |
|---|---|---|---|
| NGM Algorithm [42] | 4 | 0.081 | (6, 79, 294, 332) |
| Clustering algorithm [20] | 94* | 0.025 | (1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 14, 16, 31, 47) |
| MADWN | 124 | 0.022 | (1, 2, 3, 4, 5, 6, 7, 9, 11, 12, 13, 14, 19, 21) |
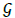 in Reference [20] consists of 70 modules; the rest of the miRNAs form 24 modules.
in Reference [20] consists of 70 modules; the rest of the miRNAs form 24 modules.Table 3: Comparison of the three methods in context of finding the modules of densely connected weighted miRNA co-target network. The number of components or modules N(q) obtained with the corresponding modularity Q(q) are mentioned along with the sizes of the components for each of the algorithms.
Further, the authors have analyzed these 70 clusters and claimed that they are biologically relevant-either pathway or tissue or disease specific. Note that, even though the targets are predicted based on sequence similarities, the microRNA clusters reveals functionality quite well; only about 11 clusters are found to contain miRNAs of identical seed sequence. Thus it is suggestive that a group of miRNA, instead of individual ones, is involved in carrying out necessary functions.
Limitations
Although the cluster finding algorithm discussed in partitions the miRNA co-target network into several components which provide significant information about the functions of miRNA clusters, it suffers from certain limitations [20]. Firstly, there exists few clusters containing a large number (as large as 47) of miRNAs; such large clusters produce significant noise in identifying pathways and functions from enhancement analysis. Secondly, if a miRNA cluster has two or more sub-structures which are connected by a few links having weights much larger than q*, it is beyond the scope of this algorithm to resolve them. For example the network in Figure 1 clearly has two modules but weight of the few links that joins the two modules are larger than q*. Since the algorithm looks for disconnected components of the graph, it is not possible to uncover these two obvious modules (A and B). Lastly to reveal the sub-structures of a giant cluster G, q is increase to an arbitrary value (taken as 160 [20]). In practice the actual number of clusters depends weakly on this choice, however it still introduces arbitrariness in the algorithm. All these shortcomings necessitate exploring other appropriate algorithms for finding the community structure in dense weighted network.
The Proposed Algorithm
In this section we proposed a modularization algorithm for dense weighted network (MADWN). The algorithm primarily consists of two steps -first, finding the major communities and second, extracting their sub-structures.
Step I: For finding the modular structures, we consider a weighted network which is densely connected. Let the network has M nodes denoted by i= 1, 2, . . . , M and a connected pair of nodes i and j has non zero weight Wij. Thus, the network is represented by an adjacency matrix W with elements
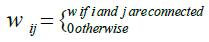 (1)
(1)
We also assume that the network is densely connected. A preliminary simplification can be done [20], where links with weights smaller than a pre-decided cutoff q are erased. The resulting network thus breaks up into smaller disconnected components -say N(q) in total. It is evident that N(q) is the number of diagonal blocks of a matrix Wq with elements
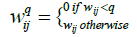 (2)
(2)
Clearly N(q) must strictly be a non-decreasing function with N(q=0)=1.
We proceed further to calculate the modularity of the concerned weighted network for different values of q. In general, if a network (weighted) has c partitions, one can calculate the modularity [42] from knowing the set of nodes which belong to each partition,
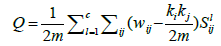 (3)
(3)
where 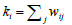 represents sum of the weights of the edges attached to node i and
represents sum of the weights of the edges attached to node i and 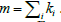 . The term S1ij is 1 only if vertices i and j belong to same group. For a given q, we take the components as the modules (thus c=N(q)) and denote corresponding modularity as Q(q). Note that, unlike N(q), the modularity Q(q) need not be an increasing function. A schematic plot of these functions are shown in Figure 2. Since, large modularity is a feature of better community structure we choose the value qm where Q(q) takes the maximum value and then collect set of components obtained there for further analysis.
. The term S1ij is 1 only if vertices i and j belong to same group. For a given q, we take the components as the modules (thus c=N(q)) and denote corresponding modularity as Q(q). Note that, unlike N(q), the modularity Q(q) need not be an increasing function. A schematic plot of these functions are shown in Figure 2. Since, large modularity is a feature of better community structure we choose the value qm where Q(q) takes the maximum value and then collect set of components obtained there for further analysis.
Step II: The number of nodes present in each of the components, i.e., the component sizes obtained at qm, are quite large. To obtain finner partitions, we find further sub-structures present in the individual components by using Newman Girvan modularization (NGM) algorithm for weighted networks [42], taking the components one by one. For each component we accept the partition if the modularity value for this partition is positive or otherwise we ignore it. Collections of all the partitioned components of the network are then considered as the final modules of the weighted network.
Example Case Studies
In this section, we use MADWN algorithm to find communities in several other real world networks, and compare them with the already known community structure. This comparative study of the modular structure of each of the real world networks considered here are found to be in good agreement with communities found earlier.
MicroRNA co-target network
First let us demonstrate this algorithm for miRNA co-target network of Homo sapiens, a dense and weighted network constructed and studied by Mookherjee et al. [20]. MicroRNAs (miRNAs) are small single stranded ~22nt long non-coding RNAs [51] that repress gene expression by binding 3’-untranslated regions (3’ UTR) of messenger RNA (mRNA) target transcripts, causing translational repression [49]. Being a secondary regulator, miRNAs usually repress the gene expression marginally. Thus it is natural to expect that cooperative action of miRNAs are needed for alteration of any biological function or pathway. MicroRNA synergism has been a recent focus in biology for studying their regulatory effects in cell. Recent articles [20,52] have identified the assemblage of the miRNAs for performing various activities. In this view finding the small clusters or communities of the miRNAs that work together for regulatory functions is quite relevant. For completeness, first we describe the construction of miRNA cotarget network briefly and then proceed for obtaining modules of this network using the MADWN algorithm discussed here.
Construction of miRNA co-target network
The miRNAs which act as secondary regulators can target more than one mRNA transcripts and a transcript can also be targeted by many miRNAs. Computationally predicted targets of miRNAs for different species are available in Microcosm Target database [50]. For constructing the miRNA network the targets of miRNAs are collected from the above mentioned database. The data predicts 34788 targets for 711 miRNAs for Homo sapiens.
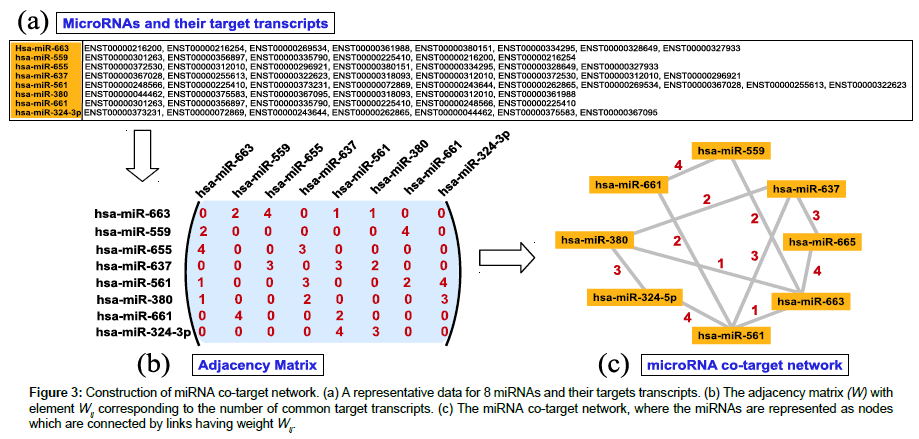
The miRNA co-target network is constructed by considering miRNAs as nodes, and a link with weight w is connected between two miRNAs if they both target w number of same target transcripts. The detailed procedure for constructing the miRNA co-target network is shown in Figure 3. The network thus formed is weighted and undirected. For convenience, miRNAs are given arbitrary, but unique, identification numbers i=1, 2,…, M, where M represents the total number of miRNAs present in the species. The miRNA cotarget network is represented as adjacency matrix W, where element Wij represents the number of mRNAs co-targeted by miRNA i and j together. Thus Wij represents the weight of the link joining the nodes i and j. If a miRNA pair i and j have no common targets, they are not connected and we set Wij=0. The diagonal elements of matrix W are taken to be zero i.e., Wij=0. The link-weights the miRNA co-target network cannot be ignored while finding the communities present in the network; the community structure depends on both weights and the connectivity of the miRNAs.
Figure 3: Construction of miRNA co-target network. (a) A representative data for 8 miRNAs and their targets transcripts. (b) The adjacency matrix (W) with element Wij corresponding to the number of common target transcripts. (c) The miRNA co-target network, where the miRNAs are represented as nodes which are connected by links having weight Wij.
Results
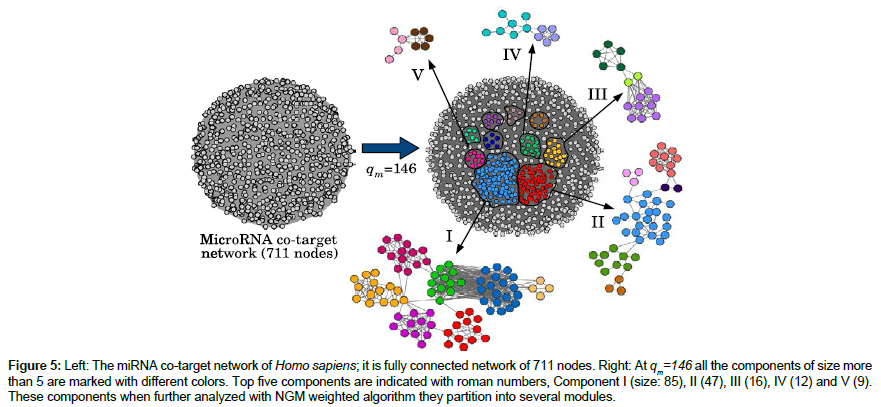
We obtain the components of miRNA co-target network using MADWN by progressively deleting the links which have weight less than q. For each q, taking the components as the communities of the graph, we calculate modularity Q(q). Figure 4 shows N(q) and Q(q) as a function of q. As expected N(q) is a non-decreasing function whereas Q(q) shows a maximum at qm=146. At q=qm, the modularity is Q(qm)=0.044 and there are 379 components, of which 284 are isolated miRNAs and the rest 95 have two or more miRNAs each (Table 1). Clearly, most of the components contain small number of miRNAs (less than 7), some have moderate number (9,12,16) and only two are large containing 47 and 85 miRNAs. In the next step we aim at finding modules of all these 95 disjoint graphs (components) individually using NGM algorithm for weighted network [42]. It turns out that only the large and moderate sized components (19 out of 95) give rise to smaller sub-structures (modules) where other components do not show any sub-structure. For example, the largest component (I in Figure 5) containing 85 miRNAs, partitions into 7 small modules of size (14,12,12,19,11,13,4) and the next largest having 47 miRNAs (Figure 5) has 6 modules of size (9,21,3,3,2,9). Partition of other three components of size 16, 12 and 9 are also shown in Figure 5 (marked as III, IV and V respectively). As a whole this algorithm results in 124 modules in total. The distribution of their sizes is given in (Table 2).
Figure 5: Left: The miRNA co-target network of Homo sapiens; it is fully connected network of 711 nodes. Right: At qm=146 all the components of size more than 5 are marked with different colors. Top five components are indicated with roman numbers, Component I (size: 85), II (47), III (16), IV (12) and V (9). These components when further analyzed with NGM weighted algorithm they partition into several modules.
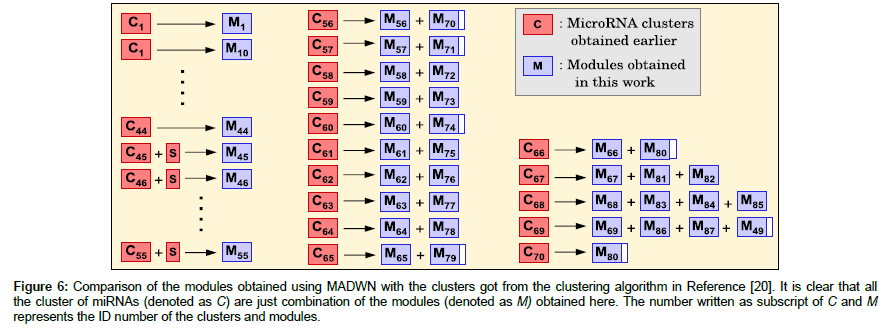
The size of the partitions obtained for miRNA co-target network of Homo sapiens using (i) NGM algorithm for weighted network [42], (ii) clustering algorithm [20] and (iii) the current work are compared in Table 3. It is evident that NGM algorithm gives the highest modularity, but the modules obtained there are very large. On the other hand, the clustering algorithm [20] gives smaller modularity value and moderate size clusters and it was claimed that these clusters are biologically relevant i.e., they are pathway, tissue or disease specific. However, some of the clusters are still very large, and it is difficult to ascertain functional specificity to these clusters. This problem is resolved in our algorithm in expense of low modularity value. Such partitions can be accepted only when the functional specifications obtained here are consistent with those obtained earlier [20]. The authors have obtained 70 clusters, each having two or more miRNAs [20]. All these clusters are found to be pathways, disease or tissue specific; for convenience, we denote them as C1, C2 ,…, C70. We analyze the miRNA contents of these 70 clusters in terms of the 124 modules obtained in this work (namely M1, M2,…, M124). If modular structure of miRNAs is different from those of the clusters, one expects that each cluster would contain miRNAs belonging from many different modules. However we find that each cluster, terms of their miRNA content, is either identical to one of the modules or composed of at most four modules. This is described in Figure 6 in details. As described in the Figure 6, clusters C1 to C44 are identical to the respective modules M1 to M44. Module M45 is same as C45 but contains one extra miRNA, marked as S in Figure 6; the same is true for modules M46 to M55. MicroRNAs of all other clusters C56 to C70 comes from two or more modules. If all miRNAs of a module participate in forming a cluster we represent it in Figure 6 by a fully shaded box, or otherwise by a partially shaded box. For example, C60 consists of all miRNAs of module M60 and some miRNAs of M74. Note that miRNAs of module M49 belong to two clusters C49 and C69; another example is M80, whose miRNAs belong to C66 and C70. This analysis revels that the modules obtained in this work are either same or very similar to those obtained [20]. Since miRNA clusters are known to be pathway and tissue specific, the modules obtained here, which are combined to form the clusters are undoubtedly biologically relevant.
Figure 6: Comparison of the modules obtained using MADWN with the clusters got from the clustering algorithm in Reference [20]. It is clear that all the cluster of miRNAs (denoted as C) are just combination of the modules (denoted as M) obtained here. The number written as subscript of C and M represents the ID number of the clusters and modules.
Scientific collaboration network
As a second example, we consider collaboration network among the scientists conducting research on network science. This collaboration network is constructed from the bibliographies of two review articles on networks [53,54].
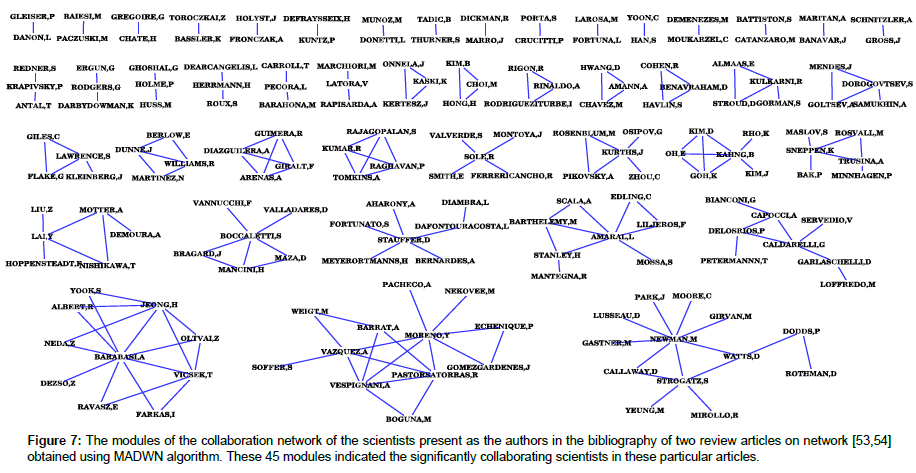
In the collaboration network, the nodes represent scientists whose names appear as authors of the articles listed in the bibliographies of [53,54] and an edge joins any two authors who are coauthors in these papers. This collaboration network consisting of 1589 scientists is multi component graph, with the largest component comprising 379 scientists, and the rest are distributed among 395 other smaller components [55]. In this current study we consider only the largest component (with 379 nodes) for finding its modular structures. The Newman Girvans modularization algorithm for weighted network [42] yields 20 modules of this network with modularity value 0.850. Whereas the application of MADWN algorithm results in 45 modules. Comparative study of these 45 modules with those obtained here by NGM algorithm for weighted network [42] and those previously obtained, implies that these components not only denotes the substructures of these modules but also identifies quite clearly the significant scientists who have strong collaborative work in these network science articles [34,55].
The MADWN algorithm in its first step determines the value of qm=53 where the modularity of the network becomes maximum by ignoring all the links that have weights less than qm. In the next step the components of this network are obtained by deleting the links having weight less than qm, and then the modular structures of all these components are found. As a result, we obtain 45 modules of this collaboration network, the scientists involved in this modules are shown in Figure 7. These set of scientists are the most significant ones in this collaboration network, and they mostly collaborate among themselves. Earlier studies [34,55] in this regard has produced similar type of modules of scientists as found presently using MADWN. But from the earlier modular structures it was not possible to identify the most significant scientists in the entire considered community, rather it could only identify the groups of scientist who worked collaboratively. Whereas in the present methodology, we could identify the most relevant scientists involved in this network, and also find the collaborations among them. Figure 7 shows in details all the 45 modules of the collaboration network obtained using MADWN algorithm; the name of the scientists present these modules are indicated for reference.
Character relationship network in novel les miserables
For the next application of MADWN algorithm to real-world network, we consider the network of characters present in the Victor Hugo’s novel Les Miserables. The dataset collected, describes the relationships between the characters in the novel of crime and redemption, Les Miserables [46,47]. In this network the nodes represent characters and a link between two nodes represents co-appearance of the corresponding characters in one or more scenes. There are in total 77 characters (nodes) in the novel and they have 257 links among themselves
The modular structure of this network was initially studied by Newman and Girvan [34] with betweenness-based hierarchical algorithm, later by Lou and Suykens [56] using a separate modularization method. When we applied NGM algorithms for weighted network [42] which uses module maximization technique to find module, it leads to 5 modules M1 (6); M2 (10); M3 (11); M4 (17); M5 (33) with sizes as indicated within the braces and the modularity value 0.547. These 5 modules are found to be similar to the ones previously observed by Lou and Suykens [56]. Although these modules could identify the frequently associated characters in the novel, but it is unable to specify the novel’s main characters. For the purpose we applied MADWN algorithm on this network.
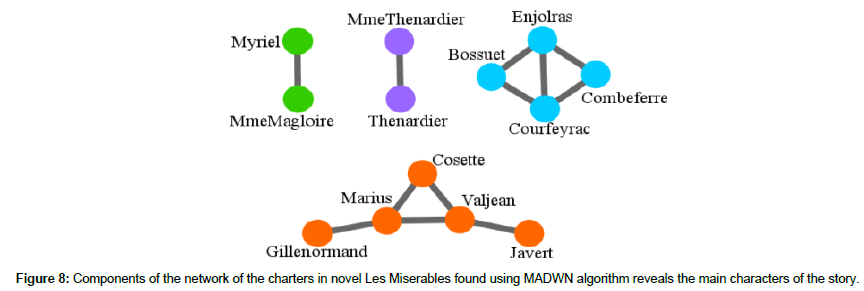
The MADWN algorithm initially ignore all the links that have weights less than qm=9; at this value of qm the modularity of the network becomes maximum. This process results in separation of 64 characters (nodes) which 484 remains as singlets and some components. The substructures of these components are further analyzed in the 486 second step of MADWN algorithm, which results in 4 small module -m1 (2); m2 (2); m3 (4); m4 (5), sizes are indicated within the bracket (Figure 8). Comparing the members of these components with those of the modules depicts that the components m1 is a sub-unit present in M2; m2 and m4 in M5 and m3 in M4. The characters in this component are seen to have high frequency of coappearance in several scenes. The novel centers around these main characters of these components, such as the protagonist Jean Valjean, the police inspector Javert, the Bishop Myriel, servant of the Bishop Madame Magloire. Thus we see that MADWN algorithm finds preciously the main characters involved in the novel Les Miserables and reflects the relation among them.
Neural network of C. elegans
In this section we apply the MADWN algorithm to another network, neural network of nematode worm C. elegans to find its underlying modular structures. The data for these neural networks of C. elegans is obtained from an article by White et al. [57]. They have considered the synaptic connectivity between neurons in the somatic nervous system except the pharynx. The data lists all the possible synaptic connections that exist between a neuron and its target neuron. This synaptic connectivity for a pair of neuron may be a chemical synapse, gap junction, or sometimes the synapse specification may be missing. It is found that a particular neuron may be connected to another neuron via (say) w synapses, but the later one may not be connected to the former by the same number of synapses. For convenience we have ignored these directionalities. For a pair of neurons we have considered all the synaptic connections possible between (former neuron to later one and the reverse) and then assigned the number of such synapses as the link weight between the consider neuron pair.
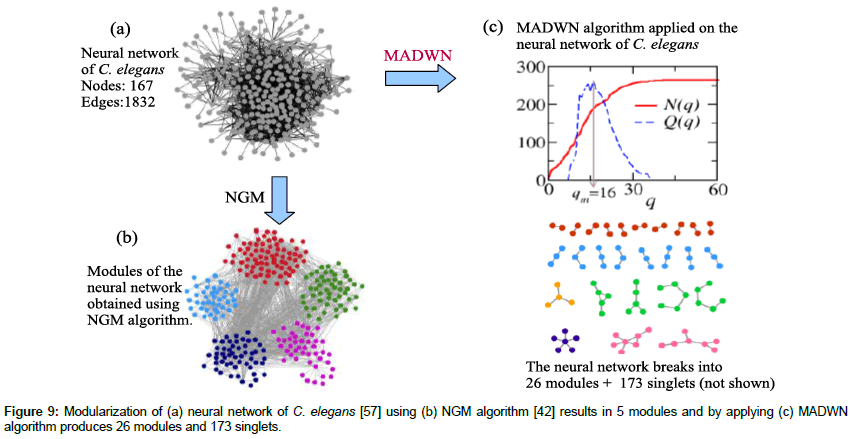
The neural network [57] consists of 265 neurons (nodes) and 1832 links (Figure 9a). The weights of these links which represents the total number of synaptic connections present between a neuron pair vary in range (1; 41); the distribution of these weights follow a power law. The modularity maximization methods cannot resolve those modules of this network which have less than 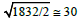 links. For example, Newman Girvans algorithm of finding modules for weighted networks [42] could find only 5 neuron modules of sizes 42,44,51,52 and 76 (Figure 9b). Thus the smaller modules which are present remain unresolved by this method. In contrary the MADWN algorithm detect 26 modules of this neural network; the module size varies from 2 to 7 (Table 4 and Figure 9c).
links. For example, Newman Girvans algorithm of finding modules for weighted networks [42] could find only 5 neuron modules of sizes 42,44,51,52 and 76 (Figure 9b). Thus the smaller modules which are present remain unresolved by this method. In contrary the MADWN algorithm detect 26 modules of this neural network; the module size varies from 2 to 7 (Table 4 and Figure 9c).
| Networks | Methods | N(q) | Q(q) | Module size (frequency) |
|---|---|---|---|---|
| B. Scientific Collaboration network [53,54] | NGM [42] | 20 | 0.850 | 5 (1), 7 (1), 8 (1), 9 (2), 10 (2), 11 (1), 17 (1), 18 (1), 20 (1), 21 (1), 22 (1), 24 (1), 25 (2), 29 (1), 33 (2), 43 (1) |
| MADWN | 45 | 0.960 | 1 (198), 2 (16), 3 (11), 4 (6), 5 (2), 6 (4), 7 (1), 8 (2), 10 (1), 12 (1), 13 (1) | |
| C. Character network in Les Miserables [47] | NGM [42] | 5 | 0.547 | 6 (1), 10 (1), 11 (1), 17 (1), 33 (1) |
| MADWN | 4 | 0.283 | 2(2), 4(1), 5 (1) | |
| D. Neural network of C. elegans [57] | NGM [42] | 5 | 0.475 | 42 (1), 44 (1), 51 (1), 52 (1), 76 (1) |
| MADWN | 26 | 0.307 | 1 (173), 2 (10), 3 (8), 4 (1), 5 (4), 6 (1) | |
| E. Email network [48] | NGM [42] | 7 | 0.402 | 2 (1), 15 (1), 17 (1), 24 (1), 25 (1), 35 (1), 49 (1) |
| MADWN | 12 | 0.321 | 1 (128), 2 (8), 3 (2), 6 (1), 11 (1) |
Table 4: Comparison of the two module finding methods NGM algorithm for weighted networks [42] and MADWAN algorithm in context of finding the modules of the following four weighted networks -scientific collaboration network [53,54], network of the character present in the novel Les Miserables [47], neural network of C. elegans [57] and Email network [48].
The MADWN algorithm initially detects qm=16 where the modularity Q(q) takes the maximum value in the process of deletion of links having weights then than a prefix value q. For every step of increase of q the corresponding components N(q) are considered as the communities and thus its modularity is calculated. Figure 9 shows the plot of N(q) and Q(q). At q=qm there are 173 singlet and 17 components of size more than 1; the next step of the algorithm disintegrates these components into further fine structures, in total 26 (Table 4 and Figure 9). Thus the MADWN algorithm is able to detect smaller modules than those obtained using NGM algorithm for weighted networks.
Email network
To evaluate the performance of MADWN algorithm we take up an email communication network [48] as fifth test network. This network is an internal email communication network between employees of a mid-sized manufacturing company. The nodes represent the employees who are sender and recipient of emails, and edges between two nodes are the individual emails. For every pair of node, one is sender and the other is recipient. Thus total number of email send from an employee to another may not be same as the number of email send by the later to the former. This implies that this email communication network is a directed one. For simplicity, we ignored directionality and assign each link a weight which equals to the sum of the total number of emails send from one employee to the other and vice versa.
This email communication network [48] consists of 167 employees (nodes), a pair of node is connected by a link if at least one of the employee has send email to the other; in total there are 3250 such links. The links in this network are given weights equal to the number of emails send between the concerned pair of employer (node). While trying to find the modules of this network, we find that the usual methods which maximize the modularity value is unable to detect small sized modules. The NGM algorithm for weighted network [42] detect 7 modules of sizes 2; 15; 17; 24; 25; 35; 49 of this email communication network.
When we applied MADWN algorithm to find the modules we obtained in total 12 modules of size more than unity and the rest 128 nodes remain as isolated nodes. These 12 modules comprises of 8 components of size 2, 2 of size 3, and one component of size 6 and 11.
Conclusion
In this article we propose an algorithm (MADWN) to detect community structure of dense weighted networks. If the network has adjacency matrix W whose elements Wij refer to the weight of the link connecting nodes i and j, one can implement the algorithm by the following steps, I. Delete all the links having weight Wij<q; find the modularity Q(q) of the network taking the disjoint components obtained here as the partitions. II. Find qm where Q(q) is maximum. III. Take all the components at q=qm containing two or more nodes one at a time, apply Newman Girvan’s weighted algorithm to obtain its modules. To demonstrate the algorithm, we consider miRNA co-target network of Homo sapiens, which is dense and weighted, and compare the modules with the miRNA clusters obtained earlier [20]. It turns out that most clusters are either identical to one of the modules, or composed of miRNAs belonging to at most four different modules. Thus, like the clusters, modules are also involved in specific biological functions.
This algorithm has certain advantage over some of the standard ones. The NGM algorithm for weighted networks [42] cannot resolve small sub-structures if the network is dense. The algorithm [20] can overcome this difficulty, but does not resolve communities which are interlinked by a few links having very large weights. The algorithm discussed here combines both the methods suitably and overcome their shortcomings. Unlike the algorithm [20], where actual number of miRNA clusters depends (though weakly) on the final choice of q (=160 [20]) this algorithm is free from parameters and provide a unique partition of the weighted miRNA co-target network. In addition, we have demonstrated the efficacy and utility of our algorithm with other four different kinds of real-world networksscientific collaboration network [34], character network in the novel Les Miserables [47], neural network of C. elegans [57], and email communication network among employees of a small company [48]. In all these example the MADWN algorithm could successfully detect the relevant components of the networks by ignoring the insignificant ones.
It has been known that a network containing l connections cannot resolve any module which has 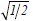 links. Usually, a densely connected weighted network, with a wide distribution of link-weights falls in this category and it is difficult to resolve small sub-structures of these networks. We believe the algorithm considered here is general, though discussed in context of miRNA co-target networks, and can be used for community detection in dense [58] and weighted [59] networks.
links. Usually, a densely connected weighted network, with a wide distribution of link-weights falls in this category and it is difficult to resolve small sub-structures of these networks. We believe the algorithm considered here is general, though discussed in context of miRNA co-target networks, and can be used for community detection in dense [58] and weighted [59] networks.
Acknowledgements
The author would like to gratefully acknowledge Prof. P. K. Mohanty from Saha Institute of Nuclear Physics, Kolkata for his constant encouragement during the work and careful reading of the manuscript. His insightful and constructive comments have helped us a lot in improving this manuscript. The author would also acknowledge the fund from Saha Institute of Nuclear Physics, Kolkata where substantial part of the work has been done.
References
- Newman MEJ (2001) The structure of scientific collaboration networks. Proc Natl Acad Sci 98: 404-409.
- Moody J (2001) Race, School Integration, and Friendship Segregation in America. Am J Sociol 107: 679-716.
- Bagler G (2008) Analysis of the airport network of India as a complex weighted network. Phys A 387: 2972-2980.
- Lämmer S, Gehlsen B, Helbing D (2006) Scaling laws in the spatial structure of urban road networks. Phys A 363: 89-95.
- Chan SHY, Donner RV, Lämmer S (2011) Urban road networks-spatial networks with universal geometric features? Eur Phys J B 84: 563-577.
- Sen P, Dasgupta S, Chatterjee A, Sreeram PA, Mukherjee G, Manna SS (2003) Small-world properties of the Indian railway network. Phys Rev E 67: 036106.
- Li W, Cai X (2007) Empirical analysis of a scale-free railway network in China. Phys A 382: 693-703.
- Albert R, Barabási AL (2002) Statistical Mechanics of complex networks. Rev Mod Phys 74: 47.
- Newman M, Barabási AL, Watts DJ (2006) The Structure and Dynamics of Networks, Princeton University Press.
- Girvan M, Newman MEJ (2002) Community structure in social and biological networks. Proc Natl Acad Sci USA 99: 7821-7826.
- Alon U (2007) Network motifs: theory and experimental approaches. Nat Rev Genet 8: 450-461.
- Cohen R, Erez K, Avraham DB, Havlin S (2000) Resilience of the Internet to Random Breakdowns. Phys Rev Lett 85: 4626.
- Cohen R, Havlin S (2010) Complex Networks: Structure, Robustness and Function, Cambridge University Press, Cambridge.
- Newman MEJ (2001) Scientific collaboration networks. I. Network construction and fundamental results. Phys Rev E 64: 016131.
- Newman MEJ (2001) Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys Rev E 64: 016132.
- Fagiolo G, Reyes J, Schiavo S (2008) On the topological properties of the world trade web: A weighted network analysis. Physica A 387: 3868-3873.
- Montis AD, Barthelemy M, Chessa A, Vespignani A (2007) The structure of Inter-Urban traffic: A weighted network analysis. Environ. Plann. B 34: 905-924.
- Barrat A, Barthélemy M, Satorras RP, Vespignani A (2004) The architecture of complex weighted networks. Proc. Natl Acad Sci USA 101: 3747-3752.
- Kumpula JM, Onnela JP, Saramäki J, Kaski K, Kertész J (2007) Emergence of Communities in Weighted Networks. Phys Rev Lett 99: 228701.
- Mookherjee S, Sinha M, Mukhopadhyay S, Bhattacharyya NP, Mohanty PK (2009) Analysis of clustered microRNA in biological pathways. Online J Bioinform 10: 280.
- Wasserman S, Faust K (1994) Social Network Analysis, Cambridge University Press, Cambridge.
- Kajikawa Y, Ohno J, Takeda Y, Matsushima K, Komiyama H (2007) Creating an academic landscape of sustainability science: an analysis of the citation network. Sustain Sci 2: 221
- Guimerà R, Stouffer DB, Sales-Pardo M, Leicht EA, Newman MEJ, et al. (2010) Origin of compartmentalization in food webs. Ecol 91: 2941-2951.
- Rezende EL, Albert EM, Fortuna MA, Bascompte J (2009) Compartments in a marine food web associated with phylogeny, body mass, and habitat structure. Ecol Lett 12: 779-788.
- Holme P, Huss M, Jeong H (2003) Subnetwork hierarchies of biochemical pathways. Bioinform. 19: 532-538.
- Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabási AL (2002) Hierarchical Organization of Modularity in Metabolic Networks. Science 297: 1551-1555.
- Kernighan BW, Lin S (1970) An efficient heuristic procedure for partitioning graphs. Bell Syst Tech J 49: 291-307.
- Fiedler M (1973) Algebraic connectivity of graphs. Czech Math J 23: 298-305.
- Pothen A, Simon HD, Liou KP (1990) Partitioning Sparse Matrices with Eigenvectors of Graphs. SIAM J. Matrix Anal Appl 11: 430-452.
- Scott J (2000) Social Network Analysis: A Handbook( 2nd edtn), Sage, London.
- Palla G, Derényi I, Farkas I, Vicsek T (2005) Uncovering the overlapping community structure of complex networks in nature and society. Nature 435: 814-815.
- Rosvall M, Bergstrom CT (2008) Maps of random walks on complex networks reveal community structure. Proc Natl Acad Sci USA 105: 1118-1123.
- Lai D, Lu H (2010) Enhanced modularity-based community detection by random walk network preprocessing. Phys Rev E 81: 066118.
- Newman MEJ, Girvan M (2004) Finding and evaluating community structure in networks. Phys Rev E 69: 026113.
- Radicchi F, Castellano C, Cecconi F, Loreto V, Parisi D (2004) Defining and identifying communities in networks. Proc Natl Acad Sci USA 101: 2658-2663.
- Donetti L, Muñoz MA (2004) Detecting network communities: a new systematic and efficient algorithm. J Stat Mech P10012.
- Danon L, Duch J, Diaz-Guilera A, Arenas A (2005) Comparing community structure identification. J Stat Mech: Theory Exp P09008.
- Blondel VD, Guillaume JL, Lambiotte R, Lefebvre E (2008) Fast unfolding of communities in large networks. J Stat Mech P10008.
- Fortunato S (2010) Community detection in graphs. Phys Rep 486: 75-174.
- Newman MEJ (2004) Fast algorithm for detecting community structure in networks. Phys Rev E 69: 066133.
- Clauset A, Newman MEJ, Moore C (2004) Finding community structure in very large networks. Phys Rev E 70: 066111.
- Newman MEJ (2004) Analysis of weighted networks. Phys Rev E 70: 056131.
- Fortunato S, Barthélemy M (2007) Resolution limit in community detection. Proc Natl Acad Sci USA 104: 36-41.
- Berry JW, Hendrickson B, LaViolette RA, Phillips CA (2011) Tolerating the community detection resolution limit with edge weighting. Phys Rev E 83: 056119.
- Basu M, Bhattacharyya NP, Mohanty PK (2011) Modules of human micro-RNA co-target network. J Phys: Conf Ser 297: 012002.
- Knuth D (1993) The Stanford GraphBase: A Platform for Combinatorial Computing. Addison-Wesley, Reading, MA.
- Victor Hugos Les Miserables dataset available
- Michalski R, Palus S, Kazienko P (2011) Lecture Notes in Business Information Processing LNBIP 87, 197.
- Farh KK, Grimson A, Jan C, Lewis BP, Johnston WK, et al. (2005) The widespread impact of mammalian MicroRNAs on mRNA repression and evolution. Science 310: 1817-1821.
- Microcosm Targets: www.ebi.ac.uk/enright-srv/microcosm/htdocs/targ ets/v5/.
- Clarke NJ, Sanseau P (2007) MicroRNA: Biology, Function and Expression, DNA Press.
- Xu J, Li CX, Li YS, Lv JY, Ma Y, et al. (2011) MiRNA-miRNA synergistic network: construction via co-regulating functional modules and disease miRNA topological features. Nucleic Acids Res 39: 825-836.
- Newman MEJ (2003) The structure and function of complex networks. SIAM Review 45: 167-256.
- Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang DU (2006) Complex networks: structure and dynamics. Physics Reports 424: 175-308.
- Newman MEJ (2006) Finding community structure in networks using the eigenvectors of matrices. Phys Rev E 74: 036104.
- Lou X, Suykens JAK (2011) Finding communities in weighted networks through synchronization. Chaos 21: 043116.
- White JG, Southgate E, Thomson JN, Brenner S (1986) The structure of the nervous system of the nematode Caenorhabditis elegans. Phil Trans R Soc London B 314.
- Basu M, Bhattacharyya NP, Mohanty PK (2013) Comparison of Modules of Wild Type and Mutant Huntingtin and TP53 Protein Interaction Networks: Implications in Biological Processes and Functions. PloS ONE 8: e64838.
- Basu M, Bhattacharyya NP, Mohanty PK (2014) Distribution of microRNA cotargets exhibit universality across a wide range of species. Europhys Lett 105: 28007.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi