Research Article, J Fashion Technol Textile Eng Vol: 5 Issue: 1
Computer Simulations of Yarn Vibrations
| Stanislav PraÄÂek* | |
| Department of textile,NTF,University of Ljubljana, Snežniška 5, SI-1000 Ljubljana, Slovenia | |
| Corresponding author : Stanislav PraÄÂek Department of textile,NTF,University of Ljubljana, Snežniška 5, SI-1000 Ljubljana, Slovenia Tel: +386 1 20 03 200 E-mail: stane.pracek@ntf.uni-lj.si |
|
| Received: December 01, 2016 Accepted: February 14, 2017 Published: February 18, 2017 | |
| Citation: PraÄÂek S (2017) Computer Simulations of Yarn Vibrations. J Fashion Technol Textile Eng 5:1. doi: 10.4172/2329-9568.1000146 |
Abstract
Vibrations in yarn, which appear when the yarn is unwinding from a package, cause many problems and can degrade the efficiency of the textile process and the quality of the end product. These vibrations in yarn are particularly strong in axial unwinding, where the package is stationary and the yarn is being withdrawn in the direction of package axis. It is thus important to find the optimum shape of the package for which the motion of the yarn will be such that vibrations in yarn will be small and as steady as possible. The unwinding will be discussed from a theoretical point of view. We will formulate the equations that describe the motion of yarn during unwinding and to construct the mathematical model which can be used to simulate the entire process of unwinding on a computer.
Keywords: Vibrations in yarn; Winding angle; Apex angle; Unwinding; Dimensionless angular velocity
Keywords |
|
| Vibrations in yarn; Winding angle; Apex angle; Unwinding; Dimensionless angular velocity | |
Introduction |
|
| The theory of yarn unwinding off a package and the balloon theory had a quick development in the fifties because of Padfield work [1,2]. She fixed Mack equations for the balloon [3] so they take into account the Coriolis system force. She found the results for a single balloon as it unwinds from a cylindrical package. Same theory was later used to calculate the parameters for multiple consecutive balloons with a nonzero unwinding angle and a cylindrical, conical or empty package [1]. Kothari and Leaf derived motion equations that include the effect of the gravity force and air resistance force tangential component [4,5]. Using extensive numerical methods for cylindrical and conical packages they showed these effects can be ignored. Recently Fraser used the motion theory to show that the time dependence can be excluded from motion equations in a mathematical correct way. He derived movable boundary conditions for packages with small winding angle. Fraser also determined that the tension inside and the radius of a balloon are smaller for an elastic yarn. Vibrations of yarn tension which appear during the yarn unwinding from stationary packages have a direct influence on the quality of the end product. All authors [1-11] who research theory of unwinding yarn from packages, used a few assumptions, which help them to set the winding angle of the packages on value 0°. In practical way, the winding angle in winding machines has values from 12° to 22°. For this reason it is almost importance to determine the package geometry and the winding angle which allow maximizing the unwinding velocity given the allowed highest vibrations in the yarn. | |
Theoretical Part |
|
| Figure 1 shows the coordinate systems and points O, Lp and Up that we will use to determine the yarn unwinding from cylindrical and conical packages. During the yarn unwinding from a stationary package, the yarn slides on the surface of the package before it lifts off to form a balloon. The point where the yarn begins to slide is known as the unwinding point Up, while the point where the yarn lifts off from the surface is known as the lift-off point Lp. On this section of the yarn, i.e. between the unwinding point and the lift-off point, the tension in the yarn drops from its value in the balloon (at the lift-off point) to its residual value, defined as the tension of the yarn inside the package. Angle φ is the winding angle of the yarn on the package. Its magnitude is the angle between the yarn at the unwinding point and the tangential direction at the package surface. From a mathematical point of view the yarn is a curve in space that can be described in a parametric form as r=r(s). Arc length s is the length of the yarn from the origin O inside the guide to the chosen point on the yarn determined with the radius vector r. The chosen point position P is time dependent (Figure 1). The equations of motion which govern the motion of the yarn are known: we have established them in one of the previous works [12]: | |
| Figure 1: Mechanical setup in over-end yarn unwinding from a cylindrical package | |
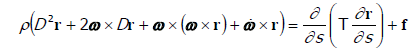 (1) (1) |
|
| Here ρ is the linear yarn mass density, i.e., the mass of the yarn per unit length which is not necessarily constant in an extensible yarn. The vector r(s,t) is the radius vector pointing to an infinitesimal section of the yarn which at time t is locate at the arc-length s away from the origin. The mechanical tension is denoted by T(s,t), and t(s,t) is the tangential vector to the yarn at the given point; it equals the partial derivative of the radius vector r with respect to the arc-length s, that is t=∂r/∂s. The vector f denotes the linear density of the external forces which are applied to the segment of yarn under discussion. In the part of the yarn that forms the balloon f is the density of the air drag force [6] and in the part of the yarn that slides on the package (between the unwinding and lift-off point) f is the density of forces with which package resists the motion of the yarn. The operator D is the differential operator of the total time derivative following the motion of a point inside a rotating coordinate system. | |
| The equation of motion (1) expressed in the dimensionless form
[6]. This consists of finding “natural” units in which to express all the
quantities appearing in the equation. A number of constants will remain
in the reduced equation and these dimensionless parameters have the
most pronounced effect on the yarn dynamics. We express all distances
in units of package radius |
|
| When we rewrite the equation of motion with these dimensionless quantities we obtain | |
| Only one parameter remains in equation (2) (without taking into account the external force term). It is the dimensionless angular velocity Ω = ωc/V. This is the single most important parameter in our model. We will show later on that we can make many important conclusions if we determine how Ω changes with time as the yarn are being unwound. There are two additional dimensionless parameters: μ, the coefficient of friction between yarn and package, and the coefficient of air resistance p0. These two parameters are approximately constant during the unwinding, so they are less important. The coefficient of friction depends on the quality of the yarn and on the surface properties of the package. The quality of the surface is comparable for forward and backward unwinding direction, so that the coefficient of friction remains approximately constant. We will show that the winding angle determines the angular velocity ω, if the unwinding velocity V and the package radius c are known. The derivation is applicable in the quasi-stationary approximation which consists of neglecting the variation of system parameters (in particular of the winding angle φ) during a single period t = 2π/ω the balloon revolves once around the axis. | |
| On cylindrical packages the angular velocity depends on the winding angle φ according to relation [2]: | |
| Introducing the dimensionless angular velocity Ω = ωc/V, this formula can also be expressed as | |
| In conical packages the relation is only slightly modified [2]: | |
| The dimensionless angular velocity can be defined as before, we obtain | |
| Here α is the apex angle of the conical package. | |
Model of Unwinding Process |
|
| During unwinding the lift-off point moves up and down the package. We can presume that the winding angle is approximately constant in the middle of the package and it changes at the edges of the package where its sign is reversed. To describe the time dependence of the winding angle we must look for a periodic function, because motion of the point is periodic to a good approximation. The most known periodic functions are trigonometric function, such as sine function. This function should be modified so that it will change only slightly when the point moves up or down the packages. We can achieve this by raising the sine to a low fractional power, say 1/40 (we have to be careful about the signs, so we take absolute value of sine function and restore the sign using the signum function: | |
| The graph of function ƒ(t) is on the Figure 2. | |
| Figure 2: Function ƒ(t) which describes the time variation of the winding angle during the unwinding from a cylindrical package. The time is express in units of the period (i.e., 2pcorresponds to one full period). Now we assume that the winding angle depends out as. | |
| φ(t) = φ0(t), (8) | |
| where φ0 is the maximal angle of wind. The function ƒ(t) has the required properties. So it is a good model for the description of packages. By this we mean the positive value of the winding angle, i.e., the characteristics of a given package. With this expression for φ(t) we can compute how the dimension-less angular velocity depends out. Equation (7) is mathematical model, which describes unwinding a yarn from packages. Equation (8) represent angle of unwinding a yarn on packages. Dimensionless angular velocity Ω = Ω(φ(t)) for cylindrical packages, see equation (4) we can write it like | |
| We can write dimensionless angular velocity Ω = Ω(φ(t)) for conical packages, see equation (6) | |
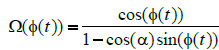 (10) (10) |
|
Results and Discussion |
|
| We will introduce the dependence of the dimensionless angular velocity Ω of cylindrical and conical packages with simulation solution. The unit of time has been chosen such that the period of unwinding is 2π. This means that from t = 0 to t = π yarn unwinds backwards (and so the dimensionless angular velocity is larger) while from t = π to t = 2π it unwinds forwards (the dimensionless angular velocity is smaller). For cylindrical parallel packages (i.e., when winding angle is close to zero) we get the straight line Ω =1. We investigated the effects of different winding angles φ and for conical packages, the apex angle α (Tables 1 and 2). | |
| Table 1: Dimensionless angular velocity as a function of the winding angle | |
| Table 2: Dimensionless angular velocity as a function of the winding angle ϕ and apex angle α. | |
| In Figure 3 we show the results for the vibrations of Ω for a range of different winding angles from 0° to 20°. In parallelly wound package (φ=0) the ω is constant, since in such packages the Ω doesn’t change with time. In package with higher winding angle φ the Ω does change with time. This happens because the angular velocity is higher when the unwinding point moves backwards as it is when the unwinding point moves forewards. We observe that the vibrations are large. For winding angle φ=20° then Ω varies from Ω=0.7002 to Ω=1.4281. In the moment when the unwinding direction changes the Ω undergoes an almost discontinuous change. Such sudden jumps lead to strong strain in the yarn, the yarn can be demaged or even broken in two parts. | |
| Figure 3: Vibrations dimensionless angular velocity Ω during the unwinding yarn from cylindrical packages, where ϕ = 0° to 20°. | |
| In Figure 4 we show the results for the yarn vibrations of Ω for unwinding from the same design of the package as in Figure 3, but this time at higher winding angles. The vibrations of Ω in the yarn that we observe in this case rise to very high values, from 1.4281 to 1.7321. At this vibration the unwinding from package with winding angles from 20° to 30° would not be possible. | |
| Figure 4: Vibrations dimensionless angular velocity Ω during the unwinding yarn from cylindrical packages, where ϕ = 20° to 30°. | |
| If we opt, instead, for packages with small winding angles, the characteristics become quite acceptable. In Figure 3c we compare the yarn vibrations of Ω from cross-wound packages with winding angles from 10° to 15°. At φ=15°, the yarn vibrations of Ω never exceeds 1.3032. In Figure 3b we plot the results for unwinding from packages with very small winding angles from 5° to 10°. We notice that for such packages the yarn vibrations of Ω remains very small, from 0.8391 to 1.1918. | |
| Figure 3a present the time dependence of the Ω for six winding angles 0°, 1°, 2°, 3°, 4° and 5°. Figure demonstrate the transition from the regime of small winding angles 0°, 1°, which are characteristic for parallel-wound packages and where the yarn vibrations of Ω tend to be negligible, to the regime of larger angles 2°, 3°, 4°, 5° where one readily observes higher vibration of Ω that characterize cross-wound packages. We obtain small vibrations of Ω for all six winding angles, that is from 0.9163 to 1.0913. | |
| Figures 3 and 4 also show the dependence of the amplitude of Ω vibrations as a function of the winding angle from 0º to 30º. For all Ω the vibrations amplitudes are larger for packages with large winding angle. In particular, the vibrations are very large for winding angles exceeding 10º. | |
| The average amplitude of the Ω can be calculated as: | |
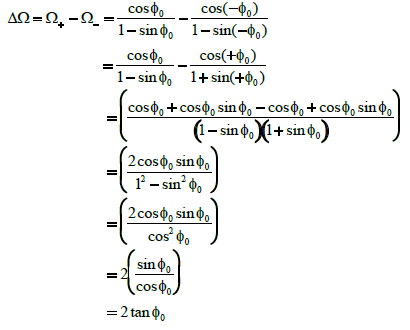 (11) (11) |
|
| Between φ0 = 0 and 0 = 0.4 rad one can approximate tan φ0 ≈ φ0 with a five percent accuracy. The accuracy is determined by the difference of the functions φ0 and tan φ0 at the point of their largest difference, i.e., at φ0 = 0.4. The relative error is then |(0.4 – tan(0.4)) / 0.4| ≈ 0.05. The angle of 0.4 rad corresponds to 23º, thus this range is appropriate for all winding angles of interest. Therefore we may approximately write | |
| ΔΩ≈2φ0 (12) | |
| This means that the amplitude of the Ω vibrations is approximately proportional to the winding angle which will change with time because this angle is different for layers that are unwinding from front towards rear edge and those that are unwinding as the unwinding point moves from the rear towards front edge. | |
| The effect of the apex angle of the cone on the dimensionless velocity is shown in Figure 5. It is clear that the effect of the typical apex angle on the dimensionless angular velocity is negligible for all practical purposes. | |
| Figure 5: Vibrations dimensionless angular velocity Ω during the unwinding yarn from conical packages, where ϕ = 10° to 30° and apex angle α = 5° to α = 10°. | |
Conclusion |
|
| We show that the winding angle influence on the vibrations in
yarn unwinding from packages. We have derived the expressions
for the time dependence of the dimensionless angular velocity of the
balloon rotation around the package axis, during the yarn unwinding
from cylindrical and conical packages. In both cases the unwinding
in the backward direction is faster than the unwinding in the forward
direction, because for the unwinding in the backward direction the
dimensionless angular velocity Ω is higher. We show dependence
dimensionless angular velocity Ω of the winding angle φ. During
unwinding the values of Ω vibration between unwinding backward
and forward. By increasing the angle φ the dimensionless angular
velocity Ω is getting higher. We showed that large vibrations of Ω
occur during yarn unwinding. We also showed that the amplitude
of Ω increases with large winding angle. To reach lower vibrations
in the yarn, we need to respect winding angle, because it has minor
act at unwinding |
|
References |
|
|
|
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi