Research Article, J Appl Bioinforma Comput Biol Vol: 9 Issue: 2
Kullback-Leibler Divergence for Medical Diagnostics Accuracy and Cut-point Selection Criterion: How it is related to the Youden Index
Hani M. Samawi1*, Jingjing Yin2, Xinyan Zhang3, Lili Yu4, Haresh Rochani5, Robert Vogel6 and Chen Mo7
Department of Biostatistics, Epidemiology and Environmental Health Sciences, Jiann-Ping Hsu College of Public Health, Georgia Southern University, Statesboro, GA 30460, USA
*Corresponding Author: Hani M. Samawi
Department of Biostatistics, Epidemiology and Environmental Health Sciences
Jiann-Ping Hsu College of Public Health, Georgia Southern University
Statesboro, GA 30460, USA
E-mail: hsamawi@georgiasouthern.edu
Received: April 22, 2020 Accepted: May 14, 2020 Published: May 21, 2020
Citation: Samawi HM, Yin J, Zhang X, Yu L, Rochani H, et al. (2020) Kullback-Leibler Divergence for Medical Diagnostics Accuracy and Cut-point Selection Criterion: How it is related to the Youden Index. J Appl Bioinforma Comput Biol 9:2.
Abstract
Recently, the Kullback-Leibler divergence (KL), which captures the disparity between two distributions, has been considered as an index for determining the diagnostic performance of markers. In this work, we propose using a total KL discrete version (TKLdiscrete), after the discretization of a continuous biomarker, as an optimization criterion for cut-point selection. We linked the proposed TKLdiscrete measure with the Youden index, which is the most commonly used cut-point selection criterion. In addition, we present theoretically and numerically the derived relations in situations of one cut-point (two categories) as well as multiple category markers under binary disease status. This study also investigates a variety of applications of KL divergence in medical diagnostics. For example, KL can serve as an overall measure of diagnostic accuracy, which measures the before-test rule-in and rule-out potential. Graphically, KL divergence depicted through the information graph. A comprehensive data analysis of the Dutch Breast Cancer Data provided to illustrate the proposed applications. Other standard Receiver Operating Characteristic (ROC) measures are also discussed and shown in the data example as competing measures. Using simulation methods, we conducted a power study to compare the performance of our proposed methods with the Youden Index
Keywords: ROC, Cut-point selection, Diagnostics, Kullback-Leibler divergence AUC, Youden Index
Keywords
ROC; Cut-point selection; Diagnostics; Kullback-Leibler divergence AUC; Youden Index
Introduction
An obvious classification rule in medical diagnostics is binary (non-diseased or diseased.) However, many biomarkers measured as continuous variables. Let X1 and X2 denote marker values for diseased and non-diseased subjects, respectively. The ROC curve is a graph of true positive rate or sensitivity (Se(c) =P (X1>c)) versus false positive rate or 1- specificity (1-Sp(c)) (sp(c) = p (X2< c)) over all possible threshold values, c, of the marker. For a continuous biomarker, the diagnostic cut-point, c, is generally required to classify a subject either as a diseased or non- diseased in making a clinical decision. We assume that, without loss of generality, higher marker values indicate greater severity of the disease. This assumption of directionality is essential for the ROC analysis to guarantee valid values of ROC indices. In practice, it is common to summarize the information of the ROC curve into a single global value or index, such as the area under (AUC), the ROC curve to evaluate the discriminatory ability of a marker. For selecting an ‘optimal’ diagnostic cut point, the Youden index (J), defined as J = max c { S e (c) +S p (c) -1},is frequently used [1]. The AUC and J have ranges of [0.5,1] and [0,1], respectively. For more details [2].
The Kullback-Leibler divergence (KL), also called information measure, or relative entropy, and measures the separation between two probability distributions. The KL considered for measuring the diagnostic performance of markers [2]. It described an application of the KL divergence for discrete biomarkers. [2] Described the KL divergence as “an abstract concept arising from statistics and information theory.” However, [3]constructed a diagrammatic interpretation of the KL divergence from Lee’s application called an ‘information graph,’ as in [4]. Information graphs demonstrate a visual basis for the evaluation and comparison of binary diagnostic tests. Such a diagrammatic interpretation of the KL divergence may make its application more appealing to clinicians.
For a binary test based on biomarker values, with the proportions of diseased subjects tested positive and non-diseased subjects tested negative in the testing categories are known and are denoted by g1 =Se(c) and g2 =Sp (c). Then, the discrete versions of KL divergence

and

can be interpreted as before-test potentials of rule-in and rule-out disease, respectively. This means a diagnostic test with a larger D (g2, g1) will, on average, a positive response makes the presence of disease more likely. A subject with a negative diagnosis resulting from a test with a large D (g2, g1) value will be more likely to be placed in the non-disease group because the potential of rule-out disease is higher. Similarly, a diagnostic test with a greater D (g1, g2) will on average have non-diseased subjects more likely to be diagnosed as negative. A subject with a positive diagnosis resulting from a test with a large D (g1, g2) value will be more likely to be placed into the disease group because the potential of rule-in disease is higher.
In this paper, we show that KL divergence for a continuous biomarker contains information about the sensitivity and the specificity of the diagnostic test (we call the discrete part) and a reminder (loss of information due to dichotomized the continuous marker at specific threshold values, c). We propose using the total KL discrete version (TKLdiscrete= D (g1, g 2)+ D (g 2, g 1)) after dichotomized of a continuous marker, as an optimization criterion for cut-point selection (optimizing the total before-test rule-in and rule-out) and link the TKLdiscrete with some the common Receiver Operating Characteristic (ROC) measures. We investigate a variety of applications of KL divergence in medical diagnostics and demonstrate how it is depicted through the information graph. We will present theoretically and numerically the relations in situations of one cutpoint (two categories) as well as multiple categories of markers under binary disease status.
The paper organized as follows: Section 2 describes preliminaries, including mathematical details of the KL divergence. In Section 3, we will show the relation between the KL divergence and some ROC indices that commonly used in medical diagnostics, with one or cutpoints. Following the difference between one and multiple cut points, we will derive how this measure used to select an optimal diagnostic threshold (cut-point). Section 4, we elaborateon the graphical interpretation of KL divergence and its proposed measures. A power analysis using simulation conducted to compare our proposed method with Youden Index as one of ROC indices in section 5. A comprehensive example is given in Section 6 to illustrate the new applications. Section 7 gives a summary and discussion.
Preliminaries Kullback-Leibler divergence for continuous marker
TheKullback-Leiblerdivergence (KL) is a numerical summary of how differently two densities f1 (x) and f 2 (x) distributed. Let f1 (x) be the probability density function (pdf) for diseased patients and f 2 (x) the pdf for the non-diseased patients. The D (f1, f2 ) discrimination information function using ( f2 ) as the reference distribution is given by

asdefined by [5].
It can be shown that D (.,.) > 0, and equality holds almost everywhere if and only if f1 (x ) = f 2 (x)therefore, the KL divergence is always non-negative, with a larger value indicating a greater separation between the two populations under consideration. It is zero if and only if the diseased and the non-diseased identically distributed concerning the diagnostic marker. In general D ( f1, f2 ) ≠ D (f2, f1) and does not possess symmetric properties. However, [6] discussed the characteristics of the symmetry properties of bi-normal and bi-gamma ROC curves in terms of the KL divergences. This measure can be applied directly to discrete distributions by replacing the integrals with summations. However, as we will demonstrate mathematically, by categorizing an inherently continuous biomarker into discrete groups, the information presented by D(.,.) is reduced.
In the case of discrete distributions,[2] defined Pin=e D(g1, g2) and Pout=e D(g2, g1) and showed that Pin is the ratio, for a randomly selected diseased subject, of the post-test disease odds to the pre-test disease odds. Whereas the P out is the ratio of the pre-test disease odds to the post-test disease odds for a randomly selected disease-free subject. Hence, Pin (Pout) (≥1) measures the increase (decrease) in disease odds after a test for disease (control) subjects. In general, since both D( f1, f2 ) and D( f2, f1 )are non-negative and are not bounded, So [7] proposed a normalized transformation of the KL divergence given by the information distinguishability measure, which can be expressed as ID ( f1, f2 ) = 1-exp [-D( f1, f2 )]. This ID measure bounded between 0 and 1, with ID = 0 indicating the marker distributions, f1(x) and f2(x) are identical, whereas ID = 1 indicates a complete separation of the marker distributions. This transformation gives a measure that is standardized, bounded, and can be used to compare different biomarkers understudy, similar to the AUC and Youden index, especially for before-test rule-in and rule-out potential.
In the next section, we will show that the T K Ldiscrete (c) measure is closely related to the sensitivity and specificity, as well as to the Youden index kernel and the natural logarithm of the diagnostic odds ratio. Thus, for continuous markers, we propose using D ( f1, f2 ) and D ( f2, f1 )as overall diagnostic accuracy measures for potential rule-in and rule-out. This is comparative to the application of sensitivity and specificity. Additionally, we propose using
T K Ldiscrete (c) as an objective function for selecting the optimal cut-point(s) to achieve the maximum information at the optimal cutoff for tests with high potential in both rule-in and rule-out situations. Similar to the application of the Youden index, which corresponds to the sum of sensitivity and specificity, TKL is the sum of rule-in and rule-out measure of accuracy.
Derivation of the Relationship of KL Divergence with Common ROC Indices
Disease and non-diseased density functions with one cut-point
In this section, we will show how D ( f1, f2 ) and D ( f2, f1 ) are related to the sensitivity and specificity and hence to other indices such as the Youden index (J) and overlap measure (Δ) [8]. Also, we will explain the rationale of using TKLdiscrete divergence measures for cut point selection.
For one cut-point, let c be any diagnostic cut point. Assuming that the diseased individual will have a value larger than c, then we define

where  is the truncated f1 density on the interval (c,∞) and
is the truncated f1 density on the interval (c,∞) and is the expected value of ln
is the expected value of ln  with respect to
with respect to  . Similarly,
. Similarly,

 (3)
(3)
where { f1c }is the truncated f1 density on the interval (−∞,c) and  is theexpected value of
is theexpected value of with respect to {f1c}. Therefore, D (f1, f2) and D (f1, f2) are based on the expected log likelihood ratio of the diseased population relative to the nondiseased population and the expected log-likelihood ratio of the nondiseased population relative to the diseased population for a given marker. Besides, we can derive the following similarly:
with respect to {f1c}. Therefore, D (f1, f2) and D (f1, f2) are based on the expected log likelihood ratio of the diseased population relative to the nondiseased population and the expected log-likelihood ratio of the nondiseased population relative to the diseased population for a given marker. Besides, we can derive the following similarly:
 (4)
(4)
and
 (5)
(5)
Finally, from (2) and (3) we have

and from (4) and (5) we have

When we dichotomize the diagnostic test at the cut point c, then as in the [2] discrete version of the two KL divergence measures we have
 (8)
(8)
and
 (9)
(9)
We interpret the above measures as follows: A diagnostic test with D ( f1, f2 ) stronger will on average make the positive diagnosis more likely among the diseased subjects (Se) in the testing population concerning false positive (1-Sp) among the non-diseased subjects. In this case, the potential of rule-in-disease is higher. This rule-in potential is the tradeoff between sensitivity (true positive) concerning false positive (1-Sp), and likewise, false negative (1-Se) concerning specificity (true negative). Whereas a diagnostic test with greater D ( f2, f1 ), will on average make positive patient. It has a higher rule-out potential.
Moreover, from (8) and (9), the total sum of the two KL divergences of the discrete versions (T K Ldiscrete (C)) is given by

However, in case of continuous markers for a given cut point (c) by adding (6) and (7) we have
 (11)
(11)
where the remainder R (C ) is given by

 (12)
(12)
Therefore, the continuous TKL is a sum of the discrete part T K Ldiscrete (C) and a non-negative remainder R(c), which is the loss of information from dichotomizing the continuous tests into a binary test at a selected diagnostic cut point. Also, this derivation demonstrates that the proposed measures of rule-in and rule-out by [2] was just the discrete part of KL measures when the continuous marker dichotomized into two distinct categories.
(i)Proposing using T K Ldiscrete (C) for the optimal cut-point selection (c) and it’s rational: It expected that when selecting a threshold/cut point for an inherently continuous biomarker by dichotomizing to create a binary disease status (non-diseased versus disease), we will inevitably lose some information [9]. However, the objective function used to estimate the cut-point (s) should be selected according to the scientific (clinical) purpose and the data context. For example, if the clinician’s goal is to use a biomarker that is more for rule-in than rule-out, then it will be more appropriate to use the optimal cut-point, which maximized T K Ldiscrete (C).Hence we propose to maximize the T K Ldiscrete (C) measure, which minimizes the remainder R(c), loss of information, concerning the cut-point value (c) across all possible values. This method can be an alternative optimization criteria for the diagnostic cut point selection in this case. Several numerical approaches can be used to find the optimal cutpoint( s) in the literature, which are available in the standard software such as SAS and R. Those methods are fast and take negligible time to find the solution. For example, we can have the maximum of T K Ldiscrete (C) by taking the first derivative with respect to c and equated to zero to find the optimal c, and check if the second derivative is negative at the maximum value c. Hence,


By setting the above derivative to zero, we can solve for the optimal c associated with TKL divergence, denoted as Ckl , that is


For applications, we can estimate the probability density functions (PDFs) and Cumulative Distribution Function (CDFs) of diseased and non-diseased groups, respectively with corresponding kernel density estimators, which are available in SAS and R. We can maximize the above equation numerically using Newton-Raphson method. For details of kernel density equations, see [10] and [11]. Alternatively, we can find the cut point by empirical searching for c: obtain the values of T K Ldiscrete (C) for each c, and chose the C =Ckl value that yields the maximum T K Ldiscrete (C). However, the latter approach may be a little slower than the other numerical methods find a link between the
TKLdiscrete (C) measure and the Youden index { J (CP)} as

where OR (CP) is the diagnostic odds ratio at the optimal cut-point associated with the Youden index and Δ is the overlap measure [8], where they showed thatΔ ( f1, f2 ) = 1- J (CP) in case of one cut-point.
(ii) Proposed diagnostic measure of accuracy based on TKL: Although, the TKL can be used to measure overall of the accuracy of the total rule-in and rule-out performance, for one cut- point of a continuous biomarker, we also propose using an overall measure of the accuracy of the total rule-in and rule-out performance, namely the maximum of as follows:

where Ckl are selected based on

KL divergence measures with multiple (k) cut-points for binary disease groups(i.e., non-diseased versus diseased)
Assuming a continuous marker has k cut-points, say {c1,c2,...,ck},then from (1)
 (13)
(13)
Using similar argument as above, we have

where 
Similarly, we have
 (15)
(15)
In addition, this derivation demonstrates that the proposed measures of ruling-in and ruling- out, by [2] for a binary disease, are just the discrete part of KL measures when the continuous marker discretized into k distinct categories. Similar to the case of one cutpoint, from (14) and (15) we have, using simple algebra,


where,

and


Again, in this case, we propose an overall measure of diagnostic accuracy for rule-in and rule-out, namely the maximum of (TKLdiscrete(c1,c2,...,ck) as

where c’=(c1,c2,...,ck) are selected based on

Table 1 illustrates the pattern of decreasing loss of information when we increase the number of cut points for categorizing the continuous marker. This again demonstrates that using the threshold points (c’) by maximizing the discrete part TKL will yield the largest information or the minimum loss of information as well as quantifying the optimal information for the ruling-in or ruling-out nature of the marker.
Table 1: Illustration of information loss using the discrete version of TKL for two exponential densities [non-diseased Exp (1) and Diseases Exp (2)], where TKL=0.5006
Numerical illustrations: Table 2 provides some numerical examples under normally distributed non-diseased and diseased populations. The values of sensitivity and specificity at the optimal cut-point associated with the Youden index. (Se(Cp) and Sp(Cp) as well as those at the cut point associated with maximum TKL discret (c) presented. We also list values of rule-in and rule-out KL divergence measures (IDin ( f1, f2 ), IDout ( f2, f1 )) and the AUC. Across all parameter settings, the sensitivity and specificity based on maximizing TKLdiscrete (c) show greater separation. In contrast, they are closer to each other when using the Youden index. Therefore, the cutoff point selection based Youden index is more balanced for the tradeoff of false positives and false negatives as the Youden index maximizes the sum of two probabilities (sensitivity and specificity).
Table 2: A numerical example of Se(cp), Se(ckl), Se(ckl), Sp(ckl), ID and AUC for two normal distributions.
On the other hand, TKL divergence minimizes the loss of information by selecting the cutoff point based on the maximizing TKLdiscrete (c) of a continuous biomarker. However, it pays less attention to the balance of the two probabilities. We suspect the reason for this imbalance is that the sensitivity and the specificity are scaled by the log(OR(c)), which will always tend to scale up the probability, whichever is more dominant
Table 2 shows that, if the diagnostic test contains any information to discriminate against the diseased from the non-diseased, the more specific tests have higher rule-in potential. In contrast, the more sensitive tests perform better at ruling out disease. This leads to the ‘rule in–specific test’ and ‘rule out–sensitive test’ principle as hypothesized.
Note that the ID values (D (.,.)) flipped when we switch the disease and non-diseased distributions and we refer this as the symmetry of KL divergence, which proven to be valid under bi-normal and bi-gamma [6].This is also true for the ROC measures sensitivity, specificity, AUC, and Youden index.
Table 3 illustrates some numerical examples when the underlying distribution of non-diseased and diseased populations considers to be exponential. As in the normal cases, the sensitivity and specificity based on TKL is further away compared with that based on the Youden index. The pattern of rule-in and rule-out potential of the disease is also the same as the observations from normal distribution. Another interesting finding is that when AUC value is close to 0.5 (AUC=0.526), both ID values are close to zero. This leads to the conclusion that diagnostic performance of a marker is close to random chance it barely has neither rule-in nor rule-out potential. Note that under bi-exponential distribution (which is a special case of bi-gamma), the ID values flipped when we switched the disease and non-diseased distributions, much like what occurred when values of ROC measures, such as sensitivity, specificity and the AUC flipped. Results from other distributions are similar.
Table 3: A numerical example of Se(cp), Sp(ckl), Sp(ckl), Sp(ckl), ID and AUC for two exponential distribution.
The Diagrammatic Interpretation of KL Divergence for Continuous Markersat a Given Cut Point (c) concerning Bregman divergence: We discuss the diagrammatic interpretation of the KL divergence at a cut point for continuous markers, which he referred to as an information graph’. In this case, the information graph provides a visual basis for the evaluation and comparison of continuous markers at each cut point. [3] showed that the construction of the information graph requires the representation of the discrete KL divergence as a discrete Bregman divergence [12]. Bregman divergences are the properties of convex functions. However, we will show that the KL divergence is the Bregman divergence associated with the negative of the Shannon entropy Function [13] when the marker is a continuous marker and related to the discrete case at a given cut point of a marker (c). The negative of the Shannon entropy Function for continuous variables is defined as.
 (16)
(16)
Define 
and  then
then

and similarly,

However, for the case of a binary diagnostic test at the cut point (c), where Sp(c) = F2(c)
and Sp(c) = F2(c) , then as in Hughes (2013) we have
I (Se(c)) = Se(c) ln (Se(c)) + (1− Se(c)) ln (1− Se(c)) and I (1− Sp(c)) = (1− Sp(c)) ln (1− Sp(c)) + Sp(c) ln (Sp(c)) In general, we can write the negative of the Shannon Entropy Function as g(P) = Pln (P) + (1− P) ln (1− P)where
P =1− Sp(c) or P = Se(c) when the reference population is the non-diseased or the disease population, respectively. To calculate Bregman divergence, we need to find a tangent of the curve
g(P1) with gradient g′(P1) = Ln(P1) − Ln(1− P1) = Slope , and an intercept g(0) = g(P1) −P1g′(P1) , drawn at point P2 (the reference point); then, we can calculate the Bregman divergence, which is the distance between the tangent and the curve at point P2. The Bregman divergence then is given by
B(P2 , P1) = g(P2) − g(P1) − (P2 − P1)g′(P1) (19)
and for the particular g (P), we will show that this is a KL divergence. For a continuous variable dichotomized at a cut point c, we have from (18) and (19)

Furthermore, we can show that B (Se(c), 1-Sp(c)) = D(Se (c),1-Sp(c)., Therefore, in the information graph, KL divergences are represented by the vertical lines between the negative Shannon entropy curve and the two tangents to the curve at Se (c) and 1-Sp(c) [3]. And this gives a theoretical basis for drawing the information graph as in Figure 2.
Finally, in the case of continuous distributions, Bregman divergence is given by

where T (t) is a strictly convex function on t. If we take T (t) = t 1n (t) then with a little algebra, we have

Simulation: To gain insight into the performance of TKL, and compare it with the Youden index (J), we conducted a simulation study to examine the empirical power under competing measures. In our simulation, we generated data from normal and gamma distributions for non-disease and disease groups. The choice of the distributions’ parameters are given in Tables 4 and 5. Scenario 1 and 2 present the case where the underlying distributions for the nondiseased and diseased groups are assumed to be identical under the null hypothesis (H0). Scenarios three through eight present the case when the underlying distributions for non-disease and disease groups considered tobe different under the null hypothesis. In the first case, the biomarker is medically irrelevant for clinicians because this type of markers cannot discriminate between the non-disease and diseased individuals with high accuracy. However, in the second case the underlying biomarker is relevant for clinicians and hence is more realistic in practice.
Table 4: Power analysis for normal underlying distribution.
Table 5: Power analysis for Gamma underlying distribution.
In our simulation, to find the critical value of those tests, under H0 and for each scenario, random samples are simulated 2000 times and the 95% quantiles for the statistics (J and TKL) are obtained. To estimate the power, 1000 replications were used. We reject the null hypothesis if the statistics estimated under the alternative hypotheses (Ha) are greater than their corresponding 95% quantiles under the null hypothesis. The sample sizes used in our simulation are n=20,50,100. Table 4 presents the results of the normal underlying distribution of the non-disease and disease population, while table 5 presents the results of the Gamma distributions. Tables 4 and 5 show that, for scenarios (1 and 3) from table 4 and (1 and 4) from table 5, both diagnostic accuracy measures, J and TKL, provide a close estimation to the nominal value of the tests (0.05). Scenario 2 in table 4 and 5, where the null hypothesis presents that non-disease and the underlying disease distributions are identical, shows that J is slightly superior to TKL measure. However, this type of biomarkers is irrelevant to medical diagnostics since they had no discrimination power. On the other hand, from scenarios 4-8 from tables 4 and 5-8 from table 5 show that TKL measure is at least as good as J in some mean shift of the underlying distribution from the null to alternative hypotheses. However, TKL is superior to J for discrimination between non-disease and disease when the underlying distributions under the null hypothesis are different in shape in general and not only in the mean shift
In general, as the distributions under H0 and Ha become more and more distant and different, the power of the tests increases. In addition, the power of the tests increases as the sample size increases. Thus our power analysis shows that TKL can capture some differences among the disease groups that J does not emphasize. Finally, the choice of the right measure for diagnostics depends not only on the power of that measure to discriminate, but also depends on the purpose of using the underlying biomarker. Our proposed TKL measure recommended as a cut-point selection criterion for several situations and when if the purpose of the diagnostics is before test rule-in and rule-out patients.
Illustration Using Dutch Breast Cancer Data: In this section, we use breast cancer gene expression data to illustrate our methods. The RNA expression of 24481 gene biomarkers measured in 295 patients with breast cancer [14]. Based on the patients’ ER and HER2 status and tumor stage, the patients divided into several subtypes. Of 295 patients, 46 belong to a basal subtype; 81 patients belong to a luminal B subtype, while 88 patients belong to a luminal A subtype. Assuming missing at random, we deleted the cases with missing measures. The basal subtype has the worst prognosis, while the luminal A subtype has the best prognosis. Luminal B has a slightly worse prognosis than luminal A, but the distinction between luminal A and B is not always obvious based on some biomarkers. A detailed description of this dataset provided in [14]. If a gene found to be expressed differently among different breast cancer subtypes, the corresponding protein product may be detectable in blood or urine. It could be the basis for a population screening test. In the following, we illustrate how KL diverge (D ( f1, f2 ), D ( f2, f1 )and TKL)and the two common ROC measures, AUC and J, can be used to determine the differentially expressed genes.
We selected two genes, AB020689 (gene marker 1) and NM_002051 (gene marker 2) to illustrate the calculations and relationship between continuous and discrete TKL maximized w.r.t. a cut-point c, as well as AUC and J with respect to the binary disease gold standard. Note all the values of AUC, J, Se, Sp as well as TKL will be estimated by the nonparametric kernel-smoothed estimates. Based on the two selected genes, the distinction between Luminal A and B is not clear, therefore, we combined luminal A and luminal B into one “non-diseased control” category as opposed to the basal subtype as “disease” category. When the mean for the diseased group (basal subtype) was less than the “non-diseased” control (luminal A or B) , we flipped the diseased and control distributions to obtain valid values of the AUC and the Youden index under the ROC analysis assumptions that the diseased subjects generally have greater marker values.
The corresponding density plots are given in Figure 1. In addition, we calculated the nonparametric kernel-smoothed estimates for KL divergences (D ( f1, f2) and D ( f2, f1)), AUC and J. We calculated six different values of KLs. Three KL divergence estimates, the total KL divergence and rule-in/rule out, for the continuous biomarker before making the test results binary based on a threshold/cutoff are calculated. The other three KL divergence estimates, the discrete TKL and rule-in/rule-out, are calculated discarding the remainder R (c) in (13), after dichotomizing the continuous biomarker into a binary diagnostic test. The two markers, marker 1 and 2, in Figure 1 had minimal location differences (similar AUCs) and small shape differences (similar total KL, AUC and Youden index values). In general, biomarker 1 and 2 are very similar in terms of overall diagnostic performance. However, after dichotomizing the biomarkers for making diagnosis, marker 2 in (b) has larger rulein potential (KLin_discrete3.04>2.24). Furthermore marker 2 in (b) has much less rule-out potential, (KLout_discrete1.69<2.05), compared with marker 1 in (a). Therefore, on average, a patient diagnosed as positive by marker 2 is 123% (exp(3.04-2.24) = 2.23) more likely to turn out as true positive compared to marker 1. Hence, marker 2 is more specific and yields less false positives compared to marker 1. Similarly, on average, a truly non-diseased individual with negative diagnosis by marker 2 is 30% (exp(1.69-2.05)=0.70 ) less likely to turn out as true negative compared to marker 1. Therefore, marker 2 is less sensitive with more false negatives.
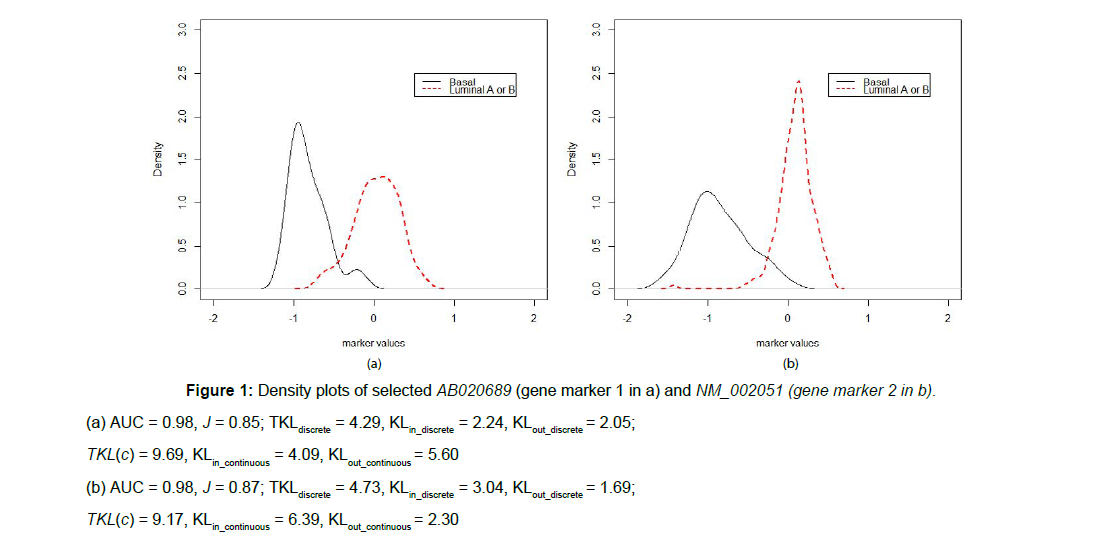
Figure 1: Density plots of selected AB020689 (gene marker 1 in a) and NM_002051 (gene marker 2 in b).
(a) AUC = 0.98, J = 0.85; TKLdiscrete = 4.29, KLin_discrete = 2.24, KLout_discrete = 2.05;
TKL(c) = 9.69, KLin_continuous = 4.09, KLout_continuous = 5.60
(b) AUC = 0.98, J = 0.87; TKLdiscrete = 4.73, KLin_discrete = 3.04, KLout_discrete = 1.69;
TKL(c) = 9.17, KLin_continuous = 6.39, KLout_continuous = 2.30
Furthermore, comparing the continuous and discrete KL values, we found that sometimes the discrete KL divergence, also the Youden index, are misleading. For the two biomarkers in Figure 1, marker 1 has larger overall information, which is not consistent with the Youden index nor with discrete when both estimated at some cutpoints. This again demonstrates the fact that by dichotomizing a continuous biomarker, we lose a certain amount of information which may lead to different conclusions. Therefore, the inconsistency between the continuous and discrete KL values may flag the incorrect number of classification needed for biomarkers. As we can see from marker 1 (a) in the Basal group is a mixture of two distributions with two modes. Hence the Basal group could be classified into two subgroups, in which case, we may have a three-disease status with two cutoff points. This TKLdiscrete based on two cut-points will be larger than the one based on only one cut-point.
Note that KLin_discrete = D (Se (c), 1-Sp (c))in (9) and KLout_discrete= D ( 1- Sp (c), Se (c)) in (10)
Another important finding is that the cutoff point based on maximizing TKLdiscrete(c), rather than on any other cutoff points, such as those based on maximizing J(c), will always minimize the loss of information by dichotomizing a continuous biomarker. Thus for marker 2, we can compare the information based on two cut points by J and by maximizing the TKLdiscrete(c), respectively, in Figure 2. The black dashed line is the shannon entropy as a function of p, any probability that ranges from 0 to 1, and the tangent lines were plotted at p=1- specificity and p=sensitivity at the cut points selected by TKLdiscrete(c) or by J using the control or the diseased population as the reference population, respectively. Note the lengths of the dashed lines are the vertical distances from the tangent points to the tangent lines, which indicate the amount of information of a biomarker making diagnosis based on cut points selected by J, red: KLin=2.82 and KLout=2.50, and by the
Figure 2: Percentage of normal coronary arteries, non-obstructive and obstructive coronary stenosis detected by CCTA in retrospective and prospective ECG-gating groups. Exact number of patients in each group is presented in parentheses above the respective bars. (1V, single vessel disease; 2V, double vessel disease; 3V, triple vessel disease; LM, left main disease; CAD, coronary artery disease)
TKLdiscrete(c), blue: KLin= 3.98 and KLout=1.97, respectively. Clearly the cut point selected by TKLdiscrete(c) gives more information, as indicated by the lengths of the two dashed blue lines (3.98+1.97>2.82+2.5), and especially larger rule-in potential, the blue line on the right, compared with the diagnosis based on the cut point selected by J for the same biomarker NM_004496 (dashed red lines). Therefore, a patient diagnosed as positive using KL divergence cut point is approximately 3.19 times, {exp(3.98-2.82) = 3.19}, more likely to turn out as true positive. Thus the KL cut point yields more specific diagnosis (Sp = 0.99) with less false positives compared with a diagnosis test using J cut point. On the other hand, a non-diseased individual diagnosed as negative by KL cut point is around 41%, exp(1.97-2.5)=0.59, less likely to turn out as true negative compared with diagnosis based on J cut point. Thus it is less sensitive with more false negatives. This indicates that different choices of cut points sometimes provide vastly different diagnosis performance. Unlike J which balances Se and Sp, KL criteria highlights the fact that marker 5 has an overall larger rule-in potential and gives more specific diagnosis at the cut point. However, in terms of overall diagnostic accuracy, even the optimization for KL is not based on maximizing (Se+Sp). We can see that the sums based on KL and J are very close.
To illustrate how the situation of multiple crossing values differs from a single threshold case, we selected another two genes, AB033062 (gene marker 3) and NM_000906 (gene marker 3), which have minimal location differences between the disease (basal) and the control (luminal A or B) groups. The KL, J and AUC estimates as well as the corresponding density plots are given in Figure 3. For gene marker 3 in Figure 3 (a), the diseased (basal) mean was less than the control (luminal A or B) mean, so we flipped the two distributions to get the estimates of AUC and the Youden index. For both markers, we can see that KL information is the maximum if we treat the biomarker as absolute continuous, the information decreases as we categorize the biomarkers for making diagnosis. The more categories (cut-points) applied, the more information is retained.
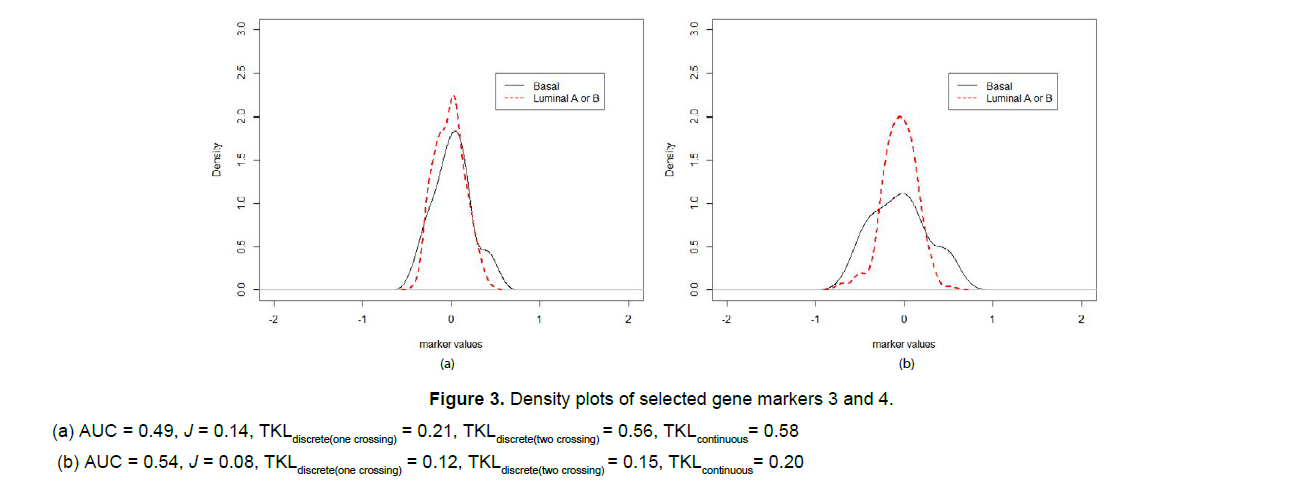
Figure 3: Density plots of selected gene markers 3 and 4.
(a) AUC = 0.49, J = 0.14, TKLdiscrete(one crossing) = 0.21, TKLdiscrete(two crossing) = 0.56, TKLcontinuous= 0.58
(b) AUC = 0.54, J = 0.08, TKLdiscrete(one crossing) = 0.12, TKLdiscrete(two crossing) = 0.15, TKLcontinuous= 0.20
Discussion
In this work, we investigated the applications of KL divergences in medical diagnostics in terms of the overall measure of before-test rule-in and rule-out potential as well as an optimization criterion for cut point(s) selection. This is an exciting and essential finding since this property of KL divergence measures can be used for diagnostic threshold selection/optimization based on a new perspective: minimizing the information loss from categorizing a continuous biomarker for making the diagnosis. Note that we usually use overall diagnostic measures such as KL divergence and AUC for selecting potential biomarkers in Phase I exploratory diagnostic accuracy studies. In addition, the surrogate biomarkers under evaluation generally used as screening tests instead of confirmatory diagnostic tests.
In general, we showed that, if the diagnostic test contains any information to discriminate against the diseased from the nondiseased, the more specific tests have higher rule-in potential. In contrast, the more sensitive tests perform better at ruling out a particular disease. This confirms the ‘rule in–specific test’ and ‘rule out–sensitive test’ principle as expected. In addition, we linked KL divergence with some common ROC measures and presented analytical and numerical relationships in the case of one cut point as well as multiple cut points. Also, we discussed the graphical interpretation of KL divergence, which is referred to as the information graph and illustrated that by using real data, as shown in Figure 2.
Moreover, we establish through numerical examples under normal and exponential distributed non-diseased and diseased populations that across all parameter settings, the sensitivity and specificity based on maximizing TKLdiscrete (c) are further away from each other. At the same time, they are closed when the Youden index used. Therefore, the cutoff selection based Youden index is more balanced for the tradeoff of false positives and false negatives as the Youden index maximizes the sum of two probabilities. On the other hand, KL minimizes the loss of information from categorized as a continuous biomarker but pays less attention to the balance of the sensitivity and the specificity probabilities. We suspect the reason for such an imbalance from KL is because the sensitivity and the specificity are scaled by the log(OR(c)), which will always tend to scale up the probability whichever is more dominant.
In the data example, we showed that continuous TKLs are greater than the discrete TKLs, which is due to the loss of information. This may have the potential of losing information, which may lead to misleading conclusions by treating a continuous biomarker as discrete for evaluation purposes. Meanwhile, by comparing one cutpoint and two cut- points for the same gene biomarkers, we show that adding more cut- points increases the information for evaluating a marker. Based on their density plots, moreover, we must include more cut- points for an accurate interpretation and application.
Finally, our power analysis showed that TKL can capture some differences among the diseases groups that J does not emphasize.
However, the choice of the right measure for diagnostics depends not only on the power of that measure to discriminate, but also depends on the purpose of using the underlying biomarker. Therefore, our proposed TKL measure is recommended if the purpose of the diagnostics is before test rule-in and rule-out patients.
References
- Zhou, Xiao-Hua, Obuchowski NA, McClish DK, et al. (2011) Statistical methods in diagnostic medicine. 2nd edition, John Whiley&Sons, Inc,Publications. New York:111-112
- Lee W-C(1999) Selecting diagnostic tests for ruling out or ruling in disease: the use of the KullbackLeibler distance. Int J Epidemiol28:521- 525
- Hughes G (2013) Information graphs for epidemiological applications of the Kullback-Leibler Divergence. Methods Inf Med 52:1342-1356.
- BenishWA(2002) The use of information graphs to evaluate and compare diagnostic tests. Methods Inf Med 41: 114 - 118.
- Kullback S, Leibler R A(1951) On information and sufficient. Ann MathStatis22:79-86
- Hughes G, Bhattacharya B (2013) Symmetry properties of Bi-Normal and Bi-Gamma receiver operating characteristic curves are described by Kullback-Leibler divergences. Entropy 15:1342-1356.
- Soofi ES, Ebrahimi N, Habibullah M (1995) Information distinguishability with application to the analysis of failure data. Journal of theAmerican Statistical Association 90: 657-668.
- Samawi HM, Yin J, Rochani H, Panchal V (2017). Notes on overlap measure as an alternative to Youden Index: How are they related? Stat Med 36:4230–4240.
- Beckstead JW, Beckie TM (2011)How much information can metabolic syndrome provide? An application of information theory. Med Decis Making31:79–92.
- Yin J, Samawi H, Linder D (2016 )Improved non-parametric estimation of diagnostic cutoff point associated with Youden index using ranked set sampling. Biometrical Journal 58:915-934
- Yin J, HaoY, Samawi H, Rochani H (2016) Rank-based kernel estimation of the area under the ROC curve. Statistical Methodology 32: 91–106.
- Bregman LM. (1967). The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. Zhvychisl Mat matFiz7:200 – 217
- Shannon CE, Weaver W (1949)The Mathematical Theory of Communication. Urbana IL: University of Illinois Press
- Van de Vijver MJ, He YD, van't Veer LJ, Dai H, A Hart AM, et al. (2002)A gene expression signature as a predictor of survival in breast cancer.N Engl J Med, 34:1999-2009.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi