Short Communication, J Fashion Technol Textile Eng S Vol: 0 Issue: 1
Loop Length Model of Fillet Structure
Olena Kyzymchuk* and Inna Ermolenko
Kyiv National University of Technologies and Design, Ukraine
Corresponding author : Olena Kyzymchuk
Kyiv National University of Technologies and Design, Nemirovich-Danchenko Street, 2, Kyiv 01011, Ukraine
E-mail: kyzymchuk_knutd@ukr.net, kyzymchuk.o@knutd.com.ua
Received: January 20, 2015 Accepted: April 25, 2015 Published: April 30, 2015
Citation: Kyzymchuk O, Ermolenko I (2015) Loop Length Model of Fillet Structure. J Fashion Technol Textile Eng S1:004. doi: 10.4172/2329-9568.S1-004
Abstract
The loop configuration that is obtained in the knit depends on both qualitative and quantitative factors, the most important of which is the loop length. Thus, it is necessary to have a geometrical model of knitted loop configuration. The aim of this research is to develop loop model for net knit structure with hexagonal cell which is formed by alternation of tricot and chain courses. Vertical ribs of such net structure consist of tricot closed loops of identical configuration while diagonal ribs consist of tricot and chain loops of different type, shape and form. In this study each loop is presented as sum of planar and spatial lines, the length of which can be easily calculated by the well-known formulas. Numerical dependences for loop length calculation are determined as a result of mathematical transformations. To verify the suggested model few variants of fillet warp knit structures were produced from polyester yarn. The investigation showed that theoretical average loop length of repeat corresponds to experimental value. It is concluded that the model can predict geometrical properties of half set two guide bar warp knitted fabric.
Keywords: Geometrical model; Warp knitting; Fillet interloping; Loop’s length
Introduction
It is well known, that unit element of a knit structure is a loop. The loop configuration that is obtained in the knit depends on both qualitative and quantitative factors, the most important of which is the loop length. The loop configuration in the knit fabric of same interlooping from yarns of the same composition and same linear density is different and varies depending on the loop length. Thus, it is necessary to have a geometrical model of knitted loop configuration.
Few studies have been undertaken on the geometry of warpknitted structures. The first geometrical model for warp knitted structures [1] was quite simple model, in which the unit stitch shape consisted of semi-circle plus two converging straight legs and straight underlap section. Second geometrical model of loop configuration was presented and improved by Grosberg for two bar warp knitted fabric [2]. It is based on physical configuration of the yarn. He assumed that the loop and underlap are effectively isolated from each other by friction, the root end of the loop lies at the widest section of the previous loop and the underlap is a part of a circle.
Other geometrical model, in which loop was described by the sum of lines, parts of circles or ellipses, was proposed by Dalidovich for single bar warp knit structure [3]. He assumed that yarn has same diameter, deformation property and a circle in the section at each part of loop. These models are flat mostly, but at real knit structure loops are unfolded, bent and curved. So it is logical to represent them as spatial curves in 3D model.
General 3D loop and underlap models for basic two-bar full-set warp knitted structures were developed by CAD program to obtain a three dimensional loop model that is suitable for visual computer representation of warp-knitted structures [4]. A 3D straight line model also should be used to predict the behavior of two-guide-bar warp knit fabric [5]. The accurate calculation of the run-in values verifies the proposed 3D loop models. But all these models were developed for full-set basic warp knit structures.
Also, it is well known, that net warp knitted fabric can be produced by using half-set two-guide-bar fillet interlooping. However, few loop configurations differ by size, form and shape in such structure [6]. In previous study, Ermolenko and Kyzymchuk [7] presented 3D loop models of net knit structure with hexagonal cell which is formed by alternation of tricot and atlas courses at repeat.
Theoretical Part
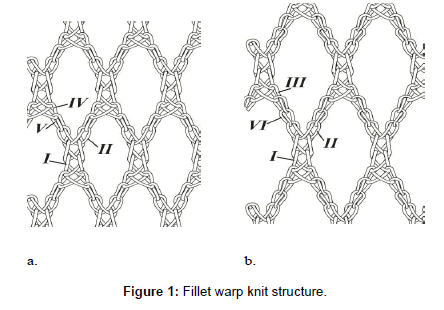
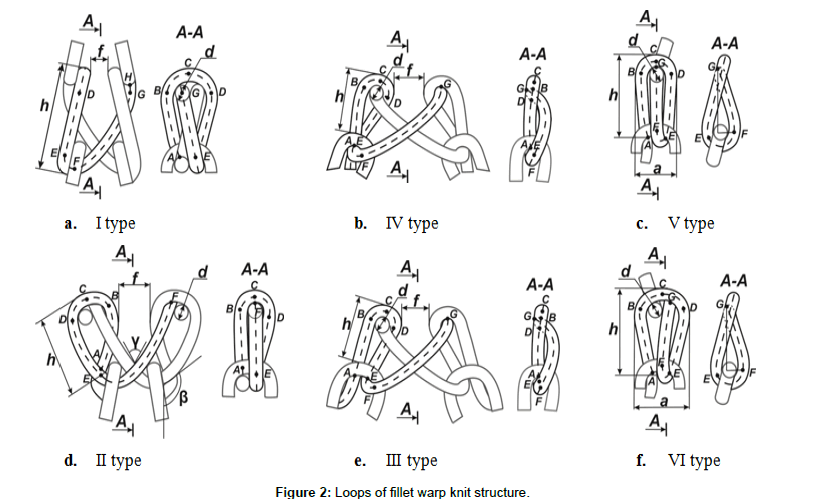
The knitted fabric that is formed by alternation of tricot and chain courses at interloping repeat has honeycomb net structure. Two variants of honeycomb structure are shown at Figure 1 which is differed by number of chain courses at repeat: one (Figure 1a) or two (Figure 1b). Vertical ribs of such net structure consist of tricot closed loops of identical configuration (type I). Loops skeletons turn from the horizontal plane to the perpendicular plane of the knitted structure (Figure 2a). Vertical rib’s length depend on number of tricot courses at interloping repeat. Diagonal ribs of cell consist of tricot (types II, III and IV) and chain (type V and VI) loops which are differing in shape and size (Figure 2b-2f). Diagonal rib’s length depends on number of chain courses at interloping repeat.
There are two regularities in alternation of loop types which have been revealed during investigating the honeycomb net warp knitted structure:
1. If interlooping repeat has consisted of odd number of chain courses, the next tricot course is formed by the closed loops, and if the interlooping repeat has consisted of an even number of chain courses, the next tricot course is formed by the opened loop;
2. The incoming and outcoming underlaps are positioning beside on loop’s arc, if next course has been formed by closed loops, and the incoming underlap is positioning behind outcoming underlap on loop’s arc, if next course has been formed by closed loops.
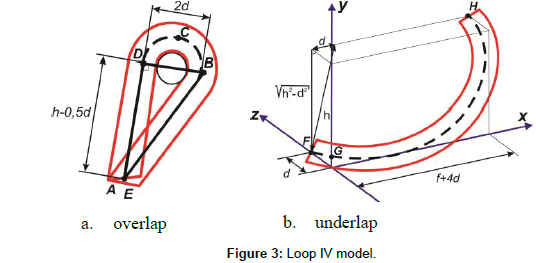
There is dependence between loop length l, yarn diameter d and loop sizes such as loop height h and distance f between two nearest loops. Loop length modelling is carried out by dividing its middle line on planar and spatial lines, the lengths of which can be easily calculated by the well-known formulas. The closed tricot loop type IV (Figure 2b) has been chosen as example for consideration of proposed model. This loop consists of sum:
loop leg AB, that is hypotenuse of triangle (Figure 3a) with legs 
loop arc BCD, that is semi-circle (Figure 3a) with radius d: BCD = πd
loop leg DE, that is equal loop height (Figure 3a): DE = h – 0,5d:
underlap EFG, that is the a spiral line (Figure 3b) with radiuses 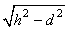 and
and 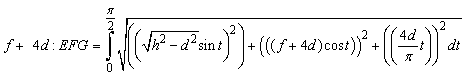
Analytical dependence Eq. (1) for loop length calculation is determined as a result of mathematical transformations:
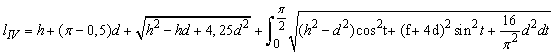 (1)
(1)
Opened loop type III (Figure 2e) differs closed loop type IV by position of loop legs, which are symmetrical and equal: AB = DE = h−0,5d. Loop IV length can be calculated by Eq. (2):
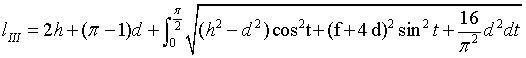 (2)
(2)
Closed tricot loop types I (Figure 2a) and II (Figure 2d) in knit structure which is formed by alternation of tricot and chain courses have same configuration as loops in knit structure which is formed by alternation of tricot and atlas courses [7]. Therefore loop lengths can be calculated by similar Eqs. (3) and (4):
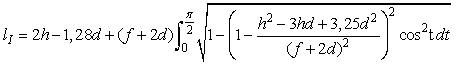 (3)
(3)
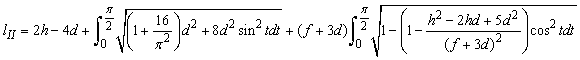 (4)
(4)
Same methods have been used for chain loops V (Figure 2c) and VI (Figure 2f) modelling. These loops are differed by loop arcs BCD. The arc of loop VI is bigger because next loop is opened and the underlaps are positioning beside. The loop arc is semi-circle with radius 1,5d. The arc of loop V is semi-circle with radius d because an ext loop is closed and the incoming underlap is positioning behind outcoming underlap on loop arc. Chain loop lengths can be calculated by Eqs. (5) and (6):
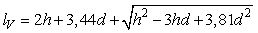 (5)
(5)
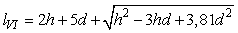 (6)
(6)
Experimental Part
In order to verify the proposed loop length model, six variant of fillet warp knit fabrics that differ by quantity of tricot and chain courses at repeat were produced from 250 denier x 2 polyester yarn. Loop height h and distance between two loops f were measured on digital microscope Microsafe Shiny Vision MM-2288-5X-BN. Experimental results are presented at Table 1.
| Courses quantity at repeat | Loop size | Loop size | |||
|---|---|---|---|---|---|
| tricot | chain | h, mm | f, mm | h, mm | f, mm |
| Loop type | I | II | |||
| 3 | 1 | 1,35 ± 0,03 | 0,63 ± 0,01 | 1,12 ± 0,04 | 1,22 ± 0,05 |
| 3 | 2 | 1,24 ± 0,03 | 0,68 ± 0,01 | 1,19 ± 0,05 | 1,14 ± 0,04 |
| 5 | 1 | 1,42 ± 0,02 | 0,65 ± 0,02 | 1,16 ± 0,03 | 1,31 ± 0,04 |
| 5 | 2 | 1,38 ± 0,02 | 0,63 ± 0,01 | 1,18 ± 0,04 | 1,46 ± 0,06 |
| 7 | 1 | 1,34 ± 0,02 | 0,66 ± 0,01 | 1,16 ± 0,02 | 1,41 ± 0,05 |
| 7 | 2 | 1,30 ± 0,02 | 0,66 ± 0,01 | 1,20 ± 0,04 | 1,47 ± 0,05 |
| average | 1,34 ± 0,06 | 0,64 ± 0,02 | 1,17 ± 0,04 | 1,33 ± 0,13 | |
| Loop type | ÆÆÆ | VI | |||
| 3 | 2 | 1,23 ± 0,02 | 0,68 ± 0,01 | 1,04 ± 0,02 | - |
| 5 | 2 | 1,28 ± 0,03 | 0,63 ± 0,01 | 1,05 ± 0,03 | - |
| 7 | 2 | 1,31 ± 0,03 | 0,66 ± 0,01 | 1,03 ± 0,03 | - |
| average | 1,27 ± 0,04 | 0,64 ± 0,02 | 1,04 ± 0,03 | - | |
| Loop type | IV | V | |||
| 3 | 1 | 1,26 ± 0,02 | 0,63 ± 0,01 | 1,02 ± 0,02 | - |
| 5 | 1 | 1,30 ± 0,03 | 0,65 ± 0,02 | 0,94 ± 0,04 | - |
| 7 | 1 | 1,29 ± 0,03 | 0,66 ± 0,01 | 0,98 ± 0,03 | - |
| average | 1,28 ± 0,03 | 0,65 ± 0,02 | 0,98 ± 0,04 | - | |
âable 1: Loop size of fillet warp knit structure.
As it is expected type I loop is higher (up to 20%) type II loop. It is a result of bending of type II loop that forms diagonal rib of cell. At the same reason the distance between I type loops as well as III and IV types is two times less than distance between type II loops. III and IV type tricot loops have same height and type VI chain loop little (up to 5%) higher type V chain loop.
Results of loop length calculation and experimental measurement for different variant of interloping repeat are shown at Tables 2 and 3. It is clear that there is a good agreement between average theoretical and experimental loop lengths.
| Quantity of tricot loops | Quantity of each type loops in repeat | Loop length, mm | Average loop length in repeat, mm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Æ | ÆÆ | ÆV | V | Æ | ÆÆ | ÆV | V | theoretical | experi-mental | % | |
| 3 | 4 | 2 | 2 | 2 | 4,82 | 4,89 | 5,57 | 3,65 | 4,75 | 4,83 ± 0,38 | 1,7 |
| 5 | 8 | 2 | 2 | 2 | 5,01 | 5,06 | 5,69 | 3,43 | 4,89 | 4,88 ± 0,18 | 0,2 |
| 7 | 12 | 2 | 2 | 2 | 4,85 | 5,16 | 5,68 | 3,54 | 4,83 | 4,80 ± 0,24 | 0,6 |
| Average | 4,89 | 5,04 | 5,65 | 3,54 | 4,82 | 4,83 ± 0,25 | 0,2 | ||||
Table 2: Loop length of fillet knit structure with 1 chain loop at repeat.
| Quantity of tricot loops | Quantity of each type loops in repeat | Loop length, mm | Average loop length in repeat, mm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Æ | ÆÆ | ÆII | VI | Æ | ÆÆ | ÆII | VI | theore-tical | experi-mental | % | |
| 3 | 4 | 2 | 2 | 4 | 4,57 | 4,99 | 5,39 | 4,13 | 4,63 | 4,78 ± 0,13 | 3,2 |
| 5 | 8 | 2 | 2 | 4 | 4,88 | 5,27 | 5,50 | 4,17 | 4,83 | 5,02 ± 0,14 | 4,0 |
| 7 | 12 | 2 | 2 | 4 | 4,73 | 5,32 | 5,61 | 4,09 | 4,75 | 4,89 ± 0,27 | 3,0 |
| Average | 4,73 | 5,20 | 5,50 | 4,13 | 4,74 | 4,99 ± 0,20 | 3,4 | ||||
Table 3: Loop length of fillet knit structure with 2 chain loop at repeat.
Conclusion
A 3D loop length model for part-set two guide bar warp knit structure has been presented. To evaluate the presented model, average loop length of fillet warp knitted fabric which is formed by alternation of tricot and chain courses at repeat were obtained theoretically and experimentally. The investigation showed that theoretical average loop length of repeat corresponds to experimental value. It can be concluded that the loop length model can predict geometrical properties of half set two guide bar warp knitted fabric.
References
- Allison GL (1958) Warp-knitting calculation made easy. Skinner’s Silk Rayon Record 32: 281-283.
- Grosberg P (1964) The geometrical properties of simple warp-knit fabric. Journal of Textile Institute 55: T18-T30.
- Dalidovich AS (1970) Basics of knitting technology. Legkaya Industriya, Moscow, Russia.
- Goktepe O, Harlock SC (2002) A 3D loop model for visual simulation of warp-knitted structures. Journal of the Textile Institute 93: 11-28.
- Dabiryan H, Jeddi AA (2011) Analysis of warp knitted fabric structure. Part 1: a 3D straight model for warp knitted fabrics. Journal of the Textile Institute 102: 1065-1074.
- Ermolenko I, Kyzymchuk O (2011) The creation of hexagonal cells in fillet knitted fabric. Bulletin of Kyiv National University of Technologies and design 1: 97-100.
- Ermolenko I, Kyzymchuk O (2013) Loop length of the fillet interlooping. Izvestiya VUZov. Technology of Light Industry 3: 3-7.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi