Research Article, J Fashion Technol Textile Eng S Vol: 0 Issue: 1
Modelling of Porosity in Knitted Fabrics
Serin Mezarciöz* and R Tuğrul Oğulata
Department of Textile Engineering, University of Cukurova, 01330 Adana, Turkey
Corresponding author: Serin Mezarciöz
Department of Textile Engineering, Faculty of Engineering and Architecture, Cukurova University, 01330, Adana, Turkey
Tel: +90 322 338 60 84; Fax: +90 322 338 61 26
E-mail: smavruz@ cu.edu.tr
Received: December 05, 2014 Accepted: April 25, 2015 Published: April 30, 2015
Citation: Mezarciöz A, Ogulata RT (2015) Modelling of Porosity in Knitted Fabrics. J Fashion Technol Textile Eng S1:005. doi:10.4172/2329-9568.S1-005
Abstract
Air permeability is defined as the volume of air (in liters) that is passed in 1 min through 100 cm (10 cmx10 cm) of the fabric at a pressure difference of 10 mm head of water. An experiment to determine the air permeability is very important as it defines the properties of keeping warm, protection against the wind, breathability etc. of knitted fabrics used as clothing. In this study, it has been attempted to establish a theoretical model for the porosity and predicted air permeability of plain knitted fabrics. A theoretical model was created to predict the porosity and air permeability of a knitted structure depending on the geometrical parameters.
Keywords: Fiber science, 3D Printing, e-textiles
Introduction
Knitting technology has advanced considerably during the past two decades with the introduction of various knitted structures, use of new and modified yarns and design of versatile knitting equipments [1]. Knit fabrics provide outstanding comfort qualities and have long been preferred as fabrics in many kinds of clothing. Since knit fabrics are produced on different machines with different knit stitches and conditions to create different patterns and fabric types, we expect them to have different qualities [2].
Air permeability is an important factor in comfort of a fabric as it plays a role in transporting moisture vapor from the skin to the outside atmosphere. The assumption is that vapor travels mainly through fabric spaces by diffusion in air from one side of the fabric to the other.
The porosity of a knitted structure will influence its physical properties such as the bulk density, the moisture absorbency, the mass transfer and the thermal conductivity.
Air flow through textiles is mainly affected by the pore characteristics of the fabrics. It is quite clear that pore dimension and distribution is a function of the fabric geometry. The yarn diameter, surface formation techniques, number of loop count for knitted fabrics per unit area are the main factors affecting the porosity of textiles. The porosity of a fabric is connected with certain important features of it, such as air permeability, water permeability, dyeing properties etc. [3].
Establishing a more complex theory to express air permeability related to all fabric parameters will have difficulties. To simplify the matter, certain important parameters such as the pore of the fabric were taken into account in the calculation of air permeability. Three factors are mainly considered that are related to the pores in fabrics.
1) Cross-sectional area of each pore
2) Depth of each pore or the thickness of the fabric and
3) The number of pores per unit area or the number of courses and wales per unit area.
In this work, these parameters are considered to develop a theoretical model for porosity and air permeability.
Materials and Methods
Materials
In order to compare the values of experimental and theoretical air permeability, we carried out 9 different knitted samples with various knitting parameters. The yarns were made of cotton fibers and the knitting type of each sample was plain. Plain knitted fabrics were on circular knitting machine compact yarns.
Knitted samples were conditioned for 48 hours in the atmospheric conditions of temperature 20 ± 2ºC and relative humidity 65 ± 2 %, before the tests were taken. Air permeability of the samples (mm/s) was measured via standard TS 391 EN ISO 9237 method, using the Textest FX 3300 air permeability tester. The measurements performed at a constant pressure drop of 100 Pa (20 cm2 test area). Also, loop length, wales per cm, courses per cm, thickness and weight of the fabrics were measured according to the relevant standards [4-7].
Methods
Theory: The calculation method of air permeability of knitted fabrics by means of Darcy’s Law was explained as follows [3]:
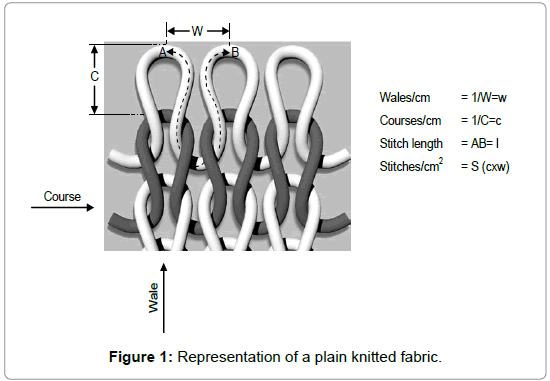
A knitted fabric consists of one or more looped yarns. Plain knitted fabric, which is illustrated in Figure 1, is one structure of knitted fabrics. W and C represent the wales spacing and course spacing whereas w and c correspond to the number of wales per cm and number of courses per cm respectively. (Wales per cm; the number of visible loops per unit length (cm) measured along a course. Courses per cm; the number of visible loops per unit length (cm) measured along a wale. Stitch length; the length of yarn in a knitted loop) (Figure 1).
The pressure gradient through a textile is a function of viscosity, density, rate of fluid flow and porosity, just as in the case of flow through a pipe [8].
The dependence of the friction coefficient f on the Reynolds Number Re for laminar and turbulent flow is described by the Blasius equation:
f = λ.Re-n (1)
where λ is the coefficient of laminar or turbulent flow, n is a coefficient indicating the flow regime.
Laminar flow: λ=64, n=1
Turbulent flow: λ=0,3164, n=0,25
The type of flow depends on Reynolds number. The Reynolds number represents the ratio of inertia force to viscous force [9].
The Reynolds number is calculated as:
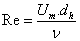 (2)
(2)
where Um is the mean flow velocity, dh is the hydraulic diameter of a pore, ν is the kinematic viscosity of the air [9,10].
The pressure drop of the flow through a duct over the thickness of the fabric is related to the friction factor f by the Darcy’s formulation.
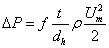 (3)
(3)
where t is the thickness of the fabric, ρ is the air density [11].
The knitted fabric is porous structure. For this reason, the air velocity in pores must be taken into consideration.
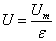 (4)
(4)
where U is the air velocity through pores, ε is rate of void area (porosity) [9].
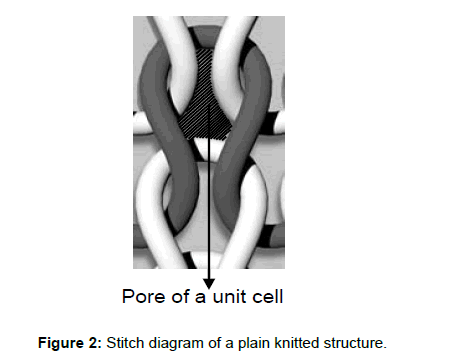
Figure 2 shows the pore within a loop. Our theoretical model was created by considering one repeating unit cell of the knitted structure. By determining the course (c) per cm, wale (w) per cm, thickness (t), yarn diameter (dy) and loop length (l), the porosity is as follows [12]:
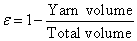 (5)
(5)
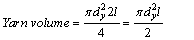 (6)
(6)
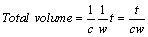 (7)
(7)
Finally,
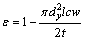
The air velocity through pores of the fabric has not usually a high value. Therefore, the fluid flow in the pores is laminar flow. For the kinetic theory, if the Reynolds number is below 2320, the flow in the tube is laminar [9,10]. For this reason, the mean air velocity through one pore can be expressed as:
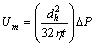 (9)
(9)
The flow rate of the air for the fabric with porous material Q becomes:
Q = m.A1.U (10)
where m is the number of pores, A1 is the cross-sectional area of pore [9]
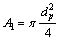 (11)
(11)
where, dp is pore diameter (In this study, the loops are assumed to be composed of ideal yarns which are circular in cross-section and have a constant diameter throughout their length, yarn deformation at crossover points is omitted, so, it is accepted dp = dh).
Thus, equation (10) can be written as follow:
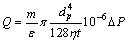 (12)
(12)
The value of air permeability (R) is calculated according to the following equation
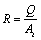 (13)
(13)
where At is the tested fabric area.
These equations which are developed in this study will be used to predict the pore size and air permeability of plain knitted fabrics.
Results and Discussion
Fabric properties (yarn number, loop length, course count per cm, wale count per cm, thickness, weight) and measured (experimental) air permeability values are presented in tabulated form in Table 1.
| Sample number |
Yarn number (tex) |
Loop length (cm) |
Course count per cm | Wale count per cm | Thickness (cm) | Weight (g/m2) |
Experimental air permeability (mm/s) |
|---|---|---|---|---|---|---|---|
| 1 | 19,72 | 0,260 | 24 | 13 | 0,0060 | 159,48 | 1532 |
| 2 | 19,72 | 0,286 | 19 | 13 | 0,0058 | 143,72 | 1647 |
| 3 | 19,72 | 0,330 | 15 | 13 | 0,0062 | 134,22 | 1948 |
| 4 | 14,79 | 0,261 | 24 | 13 | 0,0059 | 126,10 | 2459 |
| 5 | 14,79 | 0,280 | 18 | 13 | 0,0060 | 118,24 | 2966 |
| 6 | 14,79 | 0,250 | 15 | 13 | 0,0065 | 107,16 | 3708 |
| 7 | 11,83 | 0,251 | 24 | 13 | 0,0052 | 98,30 | 3128 |
| 8 | 11,83 | 0,290 | 18 | 13 | 0,0056 | 89,58 | 3306 |
| 9 | 11,83 | 0,330 | 15 | 12 | 0,0060 | 76,82 | 4616 |
Table 1: Fabric properties and experimental air permeability values.
According to the Table 1, the fabric with the lowest course count per cm and yarn number (tex) has the highest air permeability values. Therefore, rising loop length caused more looser surface in fabric increased the air permeability.
In order to predict the air permeability values for knitted fabrics, it was used the values of porosity, radius of pores and yarns and flow rate calculated via new developed equations expressed in part of the theoretical model.
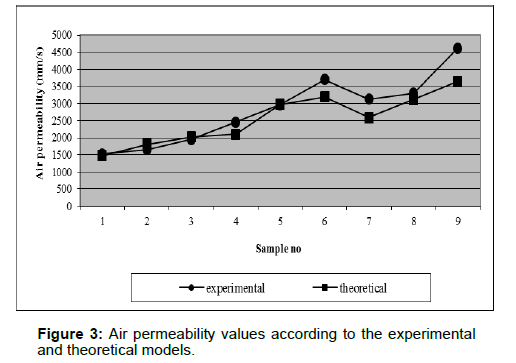
Comparing the method of theoretical model (Equation 13) and that using experimental air permeability values, we obtained the result demonstrated in Figure 3.
Conclusion
The experimental study is carried out for developing the theoretical model to predict the air permeability values for knitted fabrics. Before manufacturing, theoretical model is aimed to establish to predict the value of the air permeability via pore size and some fabric properties. Closeness of the results of the predictions based on the calculated values from the theoretical model and experimental values show that our model can be used successfully prediction of the air permeability for knitted fabrics.
References
- Kane CD, Patil UJ, Sudhakar (2007) Studies on the Influence of Knit Structure and Stitch Length on Ring and Compact Yarn Single Jersey Fabric Properties. Text Res J 77: 572-582.
- Emirhanova N, Kavusturan Y (2008) Effects of Knit Structure on the Dimensional and Physical Properties of Winter Outerwear Knitted Fabrics. Fibres & Textiles in Eastern Europe 16: 966-976.
- Ogulata RT, Mavruz S (2010) Investigation of Porosity and Air Permeability Values of Plain Knitted Fabrics. Fibres & Textiles in Eastern Europe 18: 71-75.
- TS EN 14970 (2006) Textiles - Knitted fabrics - Determination of Stitch Length and Yarn Linear Density in Weft Knitted Fabrics. Turkish Standards Institution, Turkey.
- TS EN 14971 (2006) Textiles - Knitted fabrics - Determination of Number of Stitches per Unit Length and Unit Area. Turkish Standards Institution, Turkey.
- TS 7128 EN ISO 5084 (1998) Textiles-Determination of Thickness of Textiles and Textile Products. Turkish Standards Institution,Turkey.
- TS 251 (1991) Determination of Mass per Unit Length and Mass per Unit Area, Turkish Standards Institution, Turkey.
- Booth JE (1977) Textile Mathematics. (3rd edtn), The Textile Institute, UK.
- Xu G, Wang F (2005) Prediction of the Permeability of Woven Fabrics, Journal of Industrial Textiles. 34: 243-254.
- Holman JP (1992) Heat Transfer. (7th edtn), McGraw-Hill Book Company, USA.
- TS 391 EN ISO 9237 (1999) Textiles-Determination of the Permeability of Fabrics to Air. Turkish Standards Institution, Turkey.
- Benltoufa S, Fayala F, Cheikhrouhou M, Nasrallah SB (2007) Porosity Determination of Jersey Structure, AUTEX Research Journal 7: 63-69.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi