Research Article, J Chem Appl Chem Eng Vol: 1 Issue: 2
Oxidation Number, Oxidant and Reductant as Derivative Concepts within GATES/GEB Formulation
Anna Maria MichaÅ‚owska-Kaczmarczyk1, Aneta Spórna-Kucab2 and Tadeusz MichaÅ‚owski2*
1Department of Oncology, The University Hospital in Cracow, 31-501 Cracow, Poland
2 Department of Analytical Chemistry, Technical University of Cracow, 31-155 Cracow, Poland
*Corresponding Author : Tadeusz Michałowski
Faculty of Chemical Engineering and Technology, Cracow University of Technology, Warszawska 24, 31-155 Cracow, Poland
Tel: +48126282035
E-mail: michalot@o2.pl
Received: October 23, 2017 Accepted: November 11, 2017 Published: November 18, 2017
Citation: MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A, MichaÅ‚owski T (2017) Oxidation Number, Oxidant and Reductant as Derivative Concepts Within GATES/GEB Formulation. J Chem Appl Chem Eng 1:2. doi: 10.4172/2576-3954.1000109
Abstract
Formulation of Generalized Electron Balance (GEB) according to Approach II to GEB, based on linear combination f12 = 2�??f(O) – f(H) of elemental balances: f(H) for H and f(O) for O, is illustrated on the titration of NaBr + H2SO4 (as titrand, D) with Ce(SO4)2 + H2SO4 solution (as titrant, T), according to GATES/GEB principles. Some fundamental advantages inherent in linear combination of f12 with other elemental/core balances are indicated. The prior information on oxidation numbers of all elements participating the redox system is not needed. The multipliers needed to obtain the simpler form of the balance resulting from the linear combination are equal to oxidation numbers of the elements participating the related system. This way, the f12 provides the criterion distinguishing between nonredox and redox systems. The f12 is linearly independent on other balances in a redox system, or linearly dependent in non-redox systems; the D and T are considered here as non-redox subsystems of the D+T redox system. All available physicochemical knowledge related to the D+T system can be involved in the iterative computer program used for calculation purposes.
Keywords: Redox titration; GATES/GEB; Linear combination; Oxidation number
Introduction
Redox systems are the most important/complex electrolytic systems. Redox reactions are usually coupled with acid-base, and – frequently – with complexation and/or precipitation reactions. There are redox systems with one (disproportionation, symproportionation), two or more electron-active elements. Moreover, a particular type (e.g. complexation) reaction may be exemplified by different representatives (here: ligands).
The commonly known viewpoint on titrations in electrolytic redox systems was introduced mainly in the 1960s in a series of papers by Bard and Simonsen [1], Bishop [2,3], followed by the articles of Goldman [4-10], and outlined later by Goldman [11]. The viewpoint (well-being) of those authors on their own achievements in this regard, expressed (among others) in the titles of their papers, was so amazingly contagious and convincing for the next generations of chemists, that it was replicated in numerous papers and handbooks issued later, e.g. [12-14], and in learning materials, available today in the Internet. Those elaborations/viewpoints, based on stoichiometric inferences, were totally criticized/disqualified in the review paper [15], and in [16-20].
The correct resolution of electrolytic redox systems, made according to the principles of Generalized Approach to Electrolytic Systems (GATES) [21], was presented in [15-46]. When referred to redox systems, GATES, involves the Generalized Electron Balance (GEB) in the software denoted as GATES/GEB.
Within the GATES formulation, the species in an electrolytic system are considered in their natural forms, particularly as hydrates 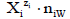 in aqueous solutions [16] (p. 520), where zi (zi = 0, ±1, ±2,…) is the charge of Xizi , expressed in terms of elementary charge unit e = F/NA (F – Faraday constant, NA – Avogadro’s constant); ni≡niW≡niH2O (≥ 0) is the mean number of water (W = H2O) molecules attached to Xizi . The known chemical formulas of the Xizi and their respective external charges provide the information necessary/sufficient to formulate the respective balances for elements or cores.
in aqueous solutions [16] (p. 520), where zi (zi = 0, ±1, ±2,…) is the charge of Xizi , expressed in terms of elementary charge unit e = F/NA (F – Faraday constant, NA – Avogadro’s constant); ni≡niW≡niH2O (≥ 0) is the mean number of water (W = H2O) molecules attached to Xizi . The known chemical formulas of the Xizi and their respective external charges provide the information necessary/sufficient to formulate the respective balances for elements or cores.
The terms: components and species are distinguished. In the notation applied here, N0j (j=1,2,…,J) is the number of molecules of the component of j-th kind, including water, forming the static or dynamic D+T system, from titrand D and titrant T composed separately. The mono- or two-phase electrolytic system thus obtained involves N1 molecules of H2O and Ni species of i-th kind, 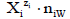 (i=2, 3,…,I), denoted briefly as Xizi (Ni,ni); then we have: H+1 (N2,n2), OH-1 (N3,n3),… .
(i=2, 3,…,I), denoted briefly as Xizi (Ni,ni); then we have: H+1 (N2,n2), OH-1 (N3,n3),… .
The process considered is the titration, where V0 mL of titrand D is titrated with V mL of titrant T; V is the volume of T added up to a defined point of the titration; the D and T are considered as subsystems of the D+T mixture thus formed. The volume of D+T at this point of the titration is V0+V, if the assumption of additivity in volumes is admitted/tolerable. The Ni species 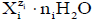 in the D+T mixture are denoted as Xizi (Ni,ni), i=2,…,I, whose molar [mol/L] concentrations are denoted as [Xizi ], and
in the D+T mixture are denoted as Xizi (Ni,ni), i=2,…,I, whose molar [mol/L] concentrations are denoted as [Xizi ], and
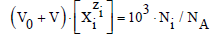 (1)
(1)
Some species in a system may involve a core, i.e., a common group/cluster of elements with defined composition, structure and external charge, that is unchanged during a process realized in the system. For example, in Ce(SO4)2 (C) + H2SO4 (C1) solution, applied as a titrant T in cerimetric [47] titrations we have, among others, the hydrated species of: HSO4-1, SO4-2, CeSO4+2, Ce(SO4)2 and Ce(SO4)3 -2, with SO4-2 as the common core.
Balancing of electrolytic systems according to GATES/GEB principles
When balancing an electrolytic system, where K different elements/cores are involved, we apply the rules of:
(a) charge conservation, expressed by charge balance, f0 = ChB, and
(b) elements/cores conservation, termed as elemental/core balances, fk = f(Yk),
where Yk is an element or core of k-th kind (k=1,…,K); in particular, we have: f1 = f(H) for Y1= H, f2 = f(O) for Y2= O.
The numbers Ni of the species are interrelated in the charge balance, f0 = ChB,
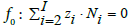 (2)
(2)
In fact, only charged species (zi≠0) enter Equation 2. The Ni and N0j are interrelated in elemental/core balances fk, written as follows
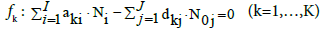 (3)
(3)
In particular, we have:
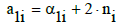 (4)
(4)
for H (k=1), where α1i is the number of H-atoms involved in Xizi, and
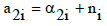 (5)
(5)
for O (k=2), where α2i is the number of O-atoms involved in Xizi. Then from Equations 4, 5 we get:
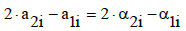 (6)
(6)
i.e., the numbers ni of water molecules are cancelled, at any i-value. From Equations 3, 6 we have the balance
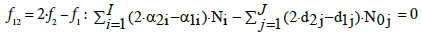 (7)
(7)
where d1j and d2j are the numbers of atoms: H and O, resp. in one molecule of the j-th component Y0j. For k=3,…,K, aki is a number of elements/cores of i-th kind in Xizi, and dkj (k=1,…,K) is a number of elements/cores of k-th kind in Y0j. Linear combination of the balances: 2, 7 and 3 for k=3,…,κ, where κ ≤ K, with pre-assumed coefficients/ multipliers mk, gives
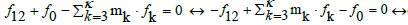 (8)
(8)
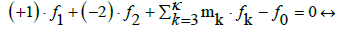 (9)
(9)
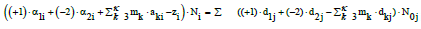 (10)
(10)
When the multipliers mk are equal to the oxidation numbers of elements in the corresponding balances (3) for k=3,…, κ, we get the simpler(st) forms of the linear combinations, not involving the species composed only from electron-non-active elements. Note that m1= +1 and m2= –2 in Equation 10 are the oxidation numbers for H and O in components and the species of the system in question [47].
It is advisable to start formulation of the system from balances interrelating the numbers N0j of particular components Yj forming V0 mL of titrand (D) and V mL of titrant (T) and the numbers Ni of particular species 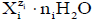 formed in the D+T mixture, at a given point of the titration.
formed in the D+T mixture, at a given point of the titration.
This article refers immediately to a dynamic redox system, considered in [48] according to the old viewpoint, commented above. The system will be formulated here according to GATES/GEB principles.
On cerimetric titration of bromide
Referring to the example raised in [48], we consider V0 mL of titrand D composed of: NaBr (N01 molecules), H2SO4 (N02 molecules) and H2O (N03 molecules), titrated with V mL of titrant T composed of Ce(SO4)2∙4H2O (N04 molecules), H2SO4 (N05 molecules) and H2O (N06 molecules). In V0+V mL of the D+T mixture thus formed we have the species:
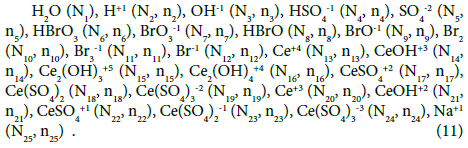
Note, for example, that:
N6 species of HBrO3∙n6H2O, denoted for brevity as HBrO3 (N6, n6), involve: N6(1+2n6) atoms of H, N6(3+n6) atoms of O, and N6 atoms of Br;
N04 molecules of Ce(SO4)2∙4H2O involve: 8N04 atoms of H, 12N04 atoms of O and O, 2N04 atoms of S, and N04 atoms of Ce.
As we see, different species are considered in their natural form, i.e. as solvates, e.g. hydrates in aqueous media. These remarks can be extended also on binary- [34,49-51] and mixed-solvent media [29,52], where formation of the species 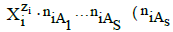 ≥0) is admitted, assuming that at least one of the co-solvents As (s ∈ <1,S>) has amphiprotic properties.
≥0) is admitted, assuming that at least one of the co-solvents As (s ∈ <1,S>) has amphiprotic properties.
Applying, for the convenience of notation, the common enumeration of the species as one presented in the set (11), we formulate the balances, separately for D, T, and D+T. We will check the properties of linear combinations of charge and elemental/core balances for each of these three solutions. Separate balancing of D and T aims to show/prove that D and T, when treated as separate solutions, are here non-redox systems.
A very useful/effective manner for checking/stating the linear dependence of the balances is the transformation of an appropriate system of equations to the identity, 0 = 0 [17,42]. To facilitate these operations, we apply the equivalent forms of the starting equations 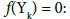
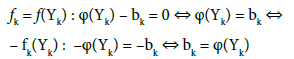
In this notation, f(Yk) will be essentially treated not as the algebraic expression on the left side of the equation f(Yk) = 0, but as an equation that can be expressed in alternative forms presented above. The equations in the form φ(Yk) – bk = 0 are applied in the minimization function of the computer program (Appendix).
Balancing of D
The balances for elements/species in D (NaBr + H2SO4 + H2O) and their linear combinations are as follows:
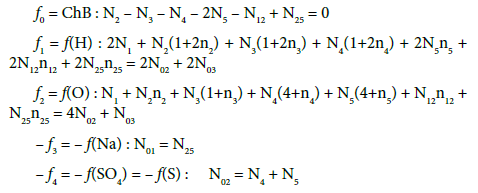
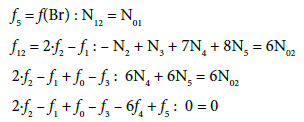
Balancing of T
The balances for elements/species in T (Ce(SO4)2∙4H2O + H2SO4 + H2O) and their linear combinations are as follows:
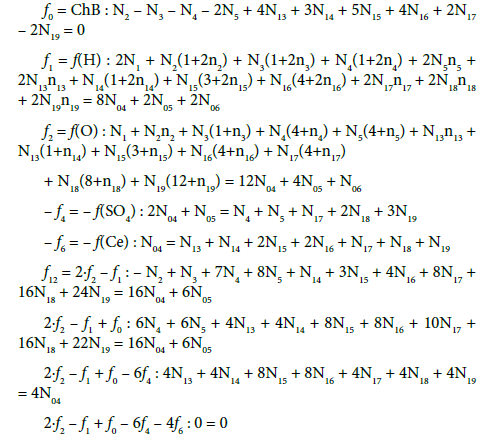
Balancing of D+T
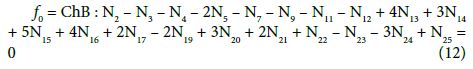
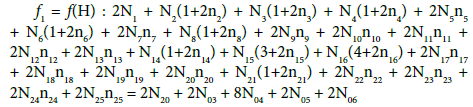
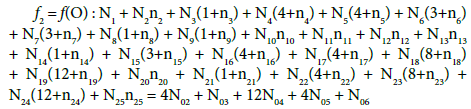
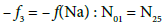 (13)
(13)
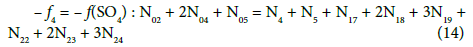
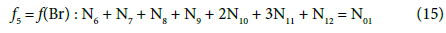
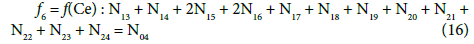
On this basis we formulate the linear combinations of the balances:
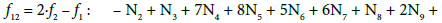
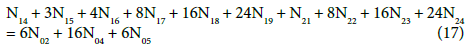
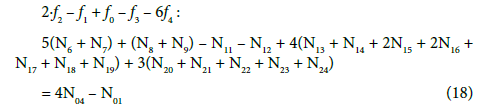
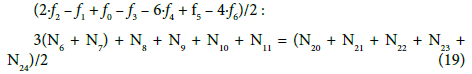
Applying atomic numbers: ZBr = 35 for Br, ZCe = 58 for Ce, we get
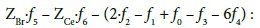
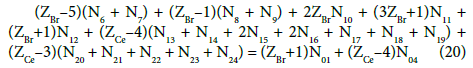
Applying the relations: Equation 1 and: C0V0 = 103∙N01/NA, CV = 103∙N04/NA, C01V0 = 103∙N02/NA, C1V = 103∙N05/NA, from the balances (12) – (20) we obtain the relations expressed in terms of molar [mol/L] concentrations:
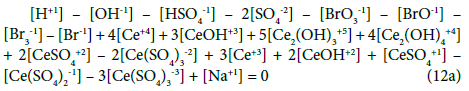
[Na+1] = C0V0/(V0+V) (13a)
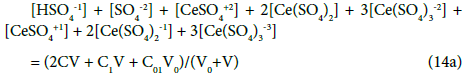
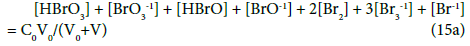
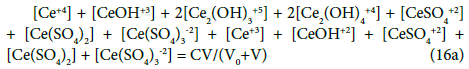
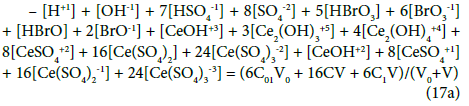
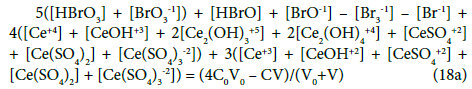
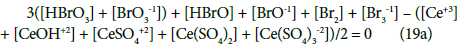
The N01 and N04 were not involved in Equation 19 and then C0 and C are not involved in Equation 19a.
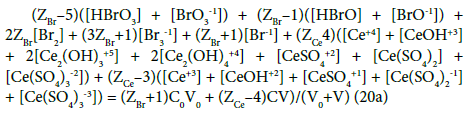
The distinguishing role of f12 = 2∙f(O) – f(H)
For all redox systems, any linear combination of f12 = 2∙f(O) – f(H) with charge balance f0 = ChB and other elemental/core balances fk = f(Yk) (k=3,…,K) related to a redox system of any degree of complexity does not give the identity, 0 = 0 [17,41,45]. The f12 is linearly dependent on f0,f3,…,fK when related to non-redox systems. In other words, the set of K independent balances f0,f12, f3,…,fK is applied for a redox system, or a set of K–1 balances f0,f3,…,fK is applied to a non-redox system with K–2 independent elemental/core balances fk = f(Yk) for Yk ≠ H, O. The independency or dependency property of f12 is then the general criterion distinguishing between redox and non-redox systems [17,28,45] of any degree of complexity, also in mixed-solvent media [29,49,52].
The difference between redox and non-redox systems is then ‘coded’ in f12. This unique, general property explains clearly why the elemental balances: f1 and f2 are not formulated for non-redox systems, of any degree of complexity. The f12 and any linear combination of f12 with f0,f3,…,fK for a given system retain full properties of the GEB. In other words, f12 is fully compatible with other (f0,f3,…,fK) balances and enables to resolve any electrolytic (mono- or/and two-phase) redox system within GATES, and GATES/GEB in particular.
All the inferences made within GATES/GEB are based on firmly established physical, physicochemical and algebraic foundations.
A choice of the independent equations and variables
Equations (17a), (18a), (19a) and (20a), are equivalent forms of the Generalized Electron Balance (GEB). This equivalence is perceived from the viewpoint of the linear combination of f12 with the balances related to the system in question. For calculations we take one of these equations. In the computer program in Appendix, the shortest balance expressed by Equation 19a, has been chosen.
The GEB (Equation 19a) completes the set of equations composed of charge balance (12a) and concentration balances for: Br (Equation 15a), Ce (Equation 16a), S (14a) – together 5 equations. The balance 13a, involving only one species, is not considered as equation, but as an equality [47], as a number that can be put, as such, into Equation 12a.
The set of independent variables is arranged in the (transposed) vector x = (E,pH,pSO4,pBr,pCe3)T, where E – potential [V], pH = –log[H+1], pSO4 = –log[SO4-2], pBr = –log[Br-1], pCe3 = –log[Ce+3]. informally, E is ascribed to GEB, pH to ChB, and pSO4, pBr, pCe3 to the related concentration balances.
The number of the (independent, ‘homogeneous’) variables equals to the number of equations, 5 = 5; this ensures a unique solution of the equations related to the system in question, at the preset C0, C, C01, C1 and V0 values, and the V-value at which the calculations are realized, at defined step of the calculation procedure offered e.g. by MATLAB [21], and realized according to the iterative computer program presented in Appendix.
On this basis, the functional dependencies: E = E(Φ), pH = pH(Φ) and speciation curves 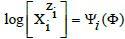 can be presented graphically for different species Xizi , where
can be presented graphically for different species Xizi , where 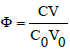 is the fraction titrated; it introduces a kind of normalization (independency on V0 value) in graphical presentation of the titrimetric procedure, compare with the related plots drawn for D+T system, where FeSO4 + H2SO4 solution as D is titrated with Ce(SO4)2 + H2SO4 solution as T [25,30].
is the fraction titrated; it introduces a kind of normalization (independency on V0 value) in graphical presentation of the titrimetric procedure, compare with the related plots drawn for D+T system, where FeSO4 + H2SO4 solution as D is titrated with Ce(SO4)2 + H2SO4 solution as T [25,30].
The Approach II to GEB versus the Approach I to GEB
GEB is perceived as a law of the matter conservation, as a relatively new Law of Nature [16,21,42]. From historical viewpoint, two equivalent approaches to GEB were applied. The Approach I to GEB is based on a “card game” principle, with electron-active elements as “players”, electron-non-active elements as “fans”, and electrons as “money”. This analogy is broadly and suggestively depicted in [42] (pp. 41-43). The transmission of electrons occurs between different species formed by players, whereas such transmission does not occur between fans (the fans’ accounts are intact). Another version of GEB is the Approach II, formulated on the basis of linear combination f12 = 2·f(O) − f(H), presented above.
In the D+T redox system considered here, Br and Ce are two electron-active elements, brought to the system in the salts: NaBr and Ce(SO4)2 ∙4H2O; the elements: H, O, Na and S are considered here as ‘fans’. W=H2O (owner of fans: H and O) is neither oxidized nor reduced in this system. N01 molecules of NaBr brings into the system (ZBr+1)N01 bromine electrons, whereas N04 molecules of Ce(SO4)2∙4H2O brings here (ZCe–4)N04 cerium electrons. The common pool of electrons brought here equals (ZBr+1)N01 + (ZCe–4)N04. A part of these electrons form new bromine species and new cerium species. It is involved with transmission of electrons as “money” between Br and Ce as “players”. W=H2O accompanies formation of oxidized forms of Br, e.g. Br-1 + 3H2O – 6e-1 = HBrO3 + 5H+1. In this reaction, O does not change its oxidation number, that is equal –2 both in H1O and in BrO3-1. Likewise, H does not change its oxidation number; it is equal +1 in H2O and in H+1. So, on a particular stage of D+T formation, N6 entities of HBrO3∙n6H2O as the species formed in this reaction contains (ZBr – 5)N6 bromine electrons, … , N24 entities of Ce(SO4)3-3∙n24H2O contains (ZCe – 3)N24 cerium electrons (see the set (2) and Equations 15, 16). Applying the summation similar to that shown in [42] (p. 22), we obtain Equation 20, and then Equation 20a. Knowing that in a system of compatible equations [17], the equation obtained by any linear combination of a given equation with other equations are equivalent to one another; we can thus conclude that the Approach I to GEB is equivalent to the Approach II to GEB [42].
GEB, charge and concentration balances, together with the set of independent equilibrium constants, provide the numerical algorithm, implemented to software packages that support advanced programming, such as MATLAB computing environment. The calculation procedure enables the desired relationships to be plotted in 2D or 3D space [36].
In the version presented above, the GEB applies to systems where no radioactive transformations occur, and the composition of a matter reflects the natural isotopic composition of individual elements. The elements preservation principle is referred to stable elements. However, an extension of GATES on some systems where nuclear (α, β-, β+, or electron capture) transformations of radioactive elements occur is possible, assuming the known decay scheme of these elements [15].
Comments on the Oxidation Numbers
The remarks resulting from the calculations presented above for D and T as the non-redox subsystems (when considered separately) of the redox D+T system (as the mixture of D and T), can be summarized as follows.
(1) Within f12 = 2∙f2 –f1 = 2∙f(O) – f(H) (Equation 11), all numbers involved with water (W=H2O), i.e., N1, N03, N06 and all ni = nW values were cancelled in D, T and D+T in aqueous media; This is an extremely advantageous situation, when perceived from the calculation viewpoint.
(2) The linear combinations: 2∙f2 –f1 + f0 –f3 – 6f4 + f5 for the titrand D and 2∙f2 – f1 + f0 – 6f4 – 4f6 for the titrant T, after multiplying by –1, can be presented in equivalent forms:
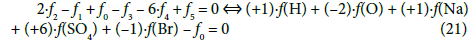
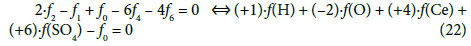
are transformed into identity, 0 = 0. The appropriately selected multipliers of the corresponding balances are equal to the oxidation numbers of the elements in the corresponding species included in these balances.
(3) The linear combination 2∙f2 –f1 + f0 –f3 – 6f4, involving all electron-non-active elements of the system, can be presented in equivalent forms:
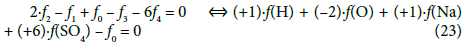
This combination (Equation 18a) involves all components and species formed by the electron-active elements of the system in question; it can be rewritten into the equivalent form
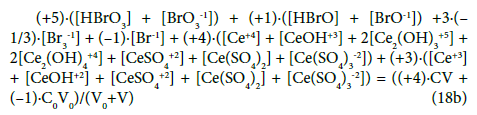
In other words, all the species involved with ‘fans’ (H, O, Na and S) were cancelled within the linear combination (23). As we see, the multipliers for concentrations of the corresponding electronactive elements (Br, Ce) in the related components and species in Equation 18b are equal to oxidation numbers of these elements in the components and species. It is the exciting property from the viewpoint of the oxidation number which, after all, is seen in chemistry as the contractual concept [55-57]. It follows naturally from a proper linear combination of charge and elemental balances, which result from the basic principles of charge and elements preservation. The Approach II shows that GEB is based on a reliable law of the elements conservation, and – in this regard – it is equally robust as equations for charge and concentration balances.
On the step of formulation of the balances according to GATES/ GEB principles, the term “oxidation number” is not ascribed to any element in a complex species present in the system considered according to Approach II to GEB; in this context, it is the redundant concept only. A known composition of all the species, expressed by their formula and external charge, provides information sufficient to formulate the related balances. These facts are of capital importance when redox equilibria are involved, e.g., with complex organic species [17]. Different species, also radicals and ion-radicals, can be included in these balances. None information about a structure of the species is needed.
The terms: oxidant and reductant are also redundant terms, not necessary (not applicable) as starting terms for further considerations on a redox system [15]. However, the oxidation degree can easily be calculated for simple compounds and species and then the Approach I to GEB is more applicable for this purpose, as a shorter (from the viewpoint of derivation only!) form of GEB. It is the case in the example of D+T system presented in this paper.
Final Comments
The Generalized Electron Balance (GEB) concept, obligatory for description of redox systems and formulated by Michałowski as the Approach I (1992) and the Approach II (2006) to GEB, is fully compatible with charge balance (ChB) and concentration balances, and complete set of relations for the corresponding equilibrium constants.
A keystone for the overall, thermodynamic knowledge on electrolytic systems is the linear combination f12 = 2·f(O) – f(H) of elemental balances: f(H) for H and f(O) for O. The 2∙f(O) – f(H) can be formulated both for non-redox and redox systems, in aqueous, non-aqueous and mixed-solvent systems, with amphiprotic (co) solvent(s) involved. The independent equation for 2·f(O) – f(H), considered as the primary form of GEB, pr-GEB = 2∙f(O) – f(H), is the basis of GEB formulation according to Approach II to GEB. The 2·f(O) – f(H) is linearly independent on ChB and other balances, for elements/cores f(Ym) ≠ H, O, in any redox system. For any non-redox system, 2·f(O) – v(H) is linearly dependent on those balances. Then the linear independency/dependency of 2·f(O) – f(H) on the other balances is the general criterion distinguishing between redox and non-redox systems.
This manner of GEB formulation needs none prior information on oxidation numbers for elements in components forming a (static or dynamic) system and in the species of the system thus formed. Within GATES/GEB, the roles of oxidants and reductants are not indicated a priori at the stage of formulation of the related balances in redox systems.
References
- Bard AJ, Simonsen SH (1960) The general equation for the equivalence point potential in oxidation-reduction titrations. J Chem Educ 37: 364-366.
- Bishop E (1962) Some theoretical considerations in analytical chemistry. Part VI. The precise calculation of data for redox titration curves. Anal Chim Acta 26: 397-405.
- Bishop E (1962) Some theoretical considerations in analytical chemistry: The influence of absolute concentration on the parameters of redox titrimetry. Anal Chim Acta 27: 253-261.
- Goldman JA (1965) The equivalence point potential in redox titrations. Anal Chim Acta 33: 217-218.
- Goldman JA (1966) A general equation for the description of redox titration curves. J Electroanal Chem 11: 255-261.
- Goldman JA (1966) Further considerations on redox titration equations. J Electroanal Chem 11: 416-424.
- Goldman JA (1967) The locations of inflection points on titration curves for symmetrical redox reactions. J Electroanal Chem 14: 373-383.
- Goldman JA (1968) Redox equilibria IV. Titration curve equations for homogeneous and symmetrical redox reactions. J Electroanal Chem 16: 47-59.
- Goldman JA (1968) Redox equilibria V. The locations of inflection points on titration curves for homogeneous reactions. J Electroanal Chem 18: 41-45.
- Goldman JA (1968) Redox equilibria VI. A completely general titration curve equation for homogenous and symmetrical redox reactions. J Electroanal Chem 19: 205-214.
- Goldman JA (1983) Oxidation reduction equilibria and titration curves, In: Treatise on analytical chemistry, Part 1, Theory and Practice. Kolthoff IM, Elving PJ (Edts) Solution Equilibria and Chemistry (Continued), Wiley, New York, 1-79.
- Butler JN, Cogley DR (1998) Ionic equilibrium: Solubility and pH calculations. J Wiley & Sons Inc, Chichester, 318-364.
- de Levie R (2001) How to use excel® in analytical chemistry and in general scientific data analysis, University Press, Cambridge.
- Burgot JL (2012) Ionic equilibria in analytical chemistry. Springer, New York, 193-418.
- MichaÅ‚owska-Kaczmarczyk AM, Asuero AG , Toporek M, MichaÅ‚owski T (2015) “Why not stoichiometry” versus “Stoichiometry – why not?” Part II. GATES in context with redox systems. Crit Rev Anal Chem 45: 240-268.
- Michałowski T, Toporek M, Michałowska-Kaczmarczyk AM, Asuero AG (2013) New trends in studies on electrolytic redox systems. Electrochimica Acta 109: 519-531.
- Cerimetry.
- Michałowska-Kaczmarczyk AM, Michałowski T (2013) Comparative balancing of non-redox and redox electrolytic systems and its consequences. Am J Analyt Chem 4: 46-53.
- Michałowski T (2010) The generalized approach to electrolytic systems: I. Physicochemical and analytical implications. Crit Rev Anal Chem 40: 2-16.
- Michałowski T, A Pietrzyk, M Ponikvar-Svet, M Rymanowski (2010) The generalized approach to electrolytic systems: II. The generalized equivalent mass (GEM) concept. Crit Rev Anal Chem 40: 17-29.
- MichaÅ‚owska-Kaczmarczyk AM, Asuero AG, MichaÅ‚owski T (2015) “Why not stoichiometry” versus “Stoichiometry – why not?” Part I. General context. Crit Rev Anal Chem 45: 166-188.
- Michałowski T (2011) Application of GATES and MATLAB for resolution of equilibrium, metastable and non-equilibrium electrolytic systems, In: Applications of MATLAB in science and engineering. Michałowski T (edt) InTech, Rijeka, Croatia, 1-34.
- Michałowski T, Baterowicz A, Madej A, Kochana J (2001) An extended Gran method and its applicability for simultaneous determination of Fe(II) and Fe(III), Anal Chim Acta 442: 287-293.
- MichaÅ‚owski T, Rymanowski M, Pietrzyk A (2005) Nontypical Brönsted’s acids and bases. J Chem Educ 82: 470-472.
- Michałowski T, Toporek M, Rymanowski M (2005) Overview on the Gran and other linearization methods applied in titrimetric analyses. Talanta 65: 1241-1253.
- Michałowski T, Kupiec K, Rymanowski M (2008) Numerical analysis of the Gran methods. A comparative study. Anal Chim Acta 606: 172-183.
- Ponikvar M, Michałowski T, Kupiec K, Wybraniec S, Rymanowski M (2008) Experimental verification of the modified Gran methods applicable to redox systems. Anal Chim Acta 628: 181-189.
- Michałowski T, Ponikvar-Svet M, Asuero AG, Kupiec K (2012) Thermodynamic and kinetic effects involved with pH titration of As(III) with iodine in a buffered malonate system. J Solution Chem 41: 436-446.
- Michałowski T, Michałowska-Kaczmarczyk AM, Toporek M (2013) Formulation of general criterion distinguishing between non-redox and redox systems. Electrochimica Acta 112: 199-211.
- Michałowska-Kaczmarczyk AM, Michałowski T (2014) Generalized electron balance for dynamic redox systems in mixed-solvent media. J Analyt Sci, Methods Instrumentation 4: 102-109.
- Michałowska-Kaczmarczyk AM, Rymanowski M, Asuero AG, Toporek M, Michałowski T (2014) Formulation of titration curves for some redox systems. Am J Analyt Chem 5: 861-878.
- Toporek M, Michałowska-Kaczmarczyk AM, Michałowski T (2014) Disproportionation reactions of HIO and NaIO in static and dynamic systems. Am J Analyt Chem 5: 1046-1056.
- Michałowska-Kaczmarczyk AM, Michałowski T (2014) GATES as the unique tool for simulation of electrolytic redox and non-redox systems. J Analytical Bioanalyt Tech 5: 1-5.
- Michałowska-Kaczmarczyk AM, Michałowski T (2015) General relation valid for electrolytic systems. JASMI 5: 74-85.
- Michałowska-Kaczmarczyk AM, Michałowski T (2014) Compact formulation of redox systems according to GATES/GEB principles. JASMI 4: 39-45.
- Michałowska-Kaczmarczyk AM, Toporek M, Michałowski T (2015) Speciation diagrams in dynamic Iodide + Dichromate system. Electrochimica Acta 155: 217-227.
- Toporek M, Michałowska-Kaczmarczyk AM, Michałowski T (2015) Symproportionation versus disproportionation in bromine redox systems. Electrochimica Acta 171: 176-187.
- MichaÅ‚owska-Kaczmarczyk AM, MichaÅ‚owski T, Toporek M, Asuero AG (2015) Why not stoichiometry” versus “Stoichiometry – why not?” Part III, Extension of GATES/GEB on complex dynamic redox systems. Crit Rev Anal Chem 45: 348-366.
- Michałowska-Kaczmarczyk AM, Michałowski T, Toporek M (2016) Formulation of dynamic redox systems according to GATES/GEB principles. Int J Electrochem Sci 11: 2560-2578.
- Meija J, Michałowska-Kaczmarczyk AM, Michałowski T (2017) Redox titration challenge. Anal Bioanal Chem 409: 11-13.
- Michałowski T, Michałowska-Kaczmarczyk AM, Meija J (2017) Solution of redox titration challenge. Anal Bioanal Chem 409(17): 4113-4115.
- MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A, MichaÅ‚owski T (2017) A general property differentiating between redox and non-redox electrolytic systems and its consequences. IJMSI 6: 67-76.
- MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A, MichaÅ‚owski T (2017) Generalized electron balance (GEB) as the law of nature in electrolytic redox systems, In: Redox: principles and advanced applications, MA Ali Khalid (edt), InTech, Rijeka, Croatia, 10-55.
- MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A , MichaÅ‚owski T (2017) Some remarks on solubility products and solubility concepts, In: Descriptive inorganic chemistry. Researches of metal compounds T Akitsu (edt), InTech, Rijeka, Croatia, 93-134.
- MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A , MichaÅ‚owski T (2017) Principles of titrimetric analyses according to GATES, In: Advances in titration techniques Vu Dang Hoang (Edt), InTech, Rijeka, Croatia, 133-171.
- MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A , MichaÅ‚owski T (2017) A distinguishing feature of the balance 2∙f(O) – f(H) in electrolytic systems. The reference to titrimetric methods of analysis, In: Advances in titration techniques, Vu Dang Hoang (edt), InTech, Rijeka, Croatia, 174-207.
- MichaÅ‚owska-Kaczmarczyk AM, Spórna-Kucab A, MichaÅ‚owski T (2017) Formulation of simple electrolytic redox systems according to GATES/ GEB principles. J Chem Appl Chem Eng 1:1.
- Whiteley Jr. RV (2015) The simulation of an oxidation−reduction titration curve with computer algebra. J Chem Educ 92: 950-953.
- Michałowski T, Pilarski B, Asuero AG , Michałowska-Kaczmarczyk AM (2014) Modeling of acid-base properties in binary-solvent systems In: Handbook of solvents. George Wypych (edt), (1stedn) ChemTec Publishing, Toronto, 623-648.
- Pilarski B, Dobkowska A, Foks H, Michałowski T (2010) Modelling of acid-base equilibria in binary-solvent systems: A comparative study. Talanta 80: 1073-1080.
- Michałowski T, Pilarski B, Dobkowska A, Młodzianowski J (2010) Mathematical modeling and physicochemical studies on acid-base equilibria in binary-solvent systems. Wiad Chem 54: 124-154.
- Michałowska-Kaczmarczyk AM, Michałowski T (2014) Linear dependence of balances for non-redox electrolytic systems. Am J Analyt Chem 5: 1285-1289.
- Lurie Yu (1971) Handbook of Analytical Chemistry, Mir Publishers, Moscow.
- Nikolsky BP (1964) Guide for Chemists: Chemical equilibrium and kinetics, In: Properties of solutions, Electrode Processes (3rdedtn), Publishing House, Moscow.
- Karen P, McArdle P, Takats J (2014) Toward a comprehensive definition of oxidation state (IUPAC Technical Report). Pure Appl Chem 86: 1017-1081.
- Karen P (2015) Oxidation state, a long-standing issue! Angew Chem Int Ed Engl 54: 4716-4726.
- Karen P, McArdle P, Takats J (2016) Comprehensive definition of oxidation state (IUPAC Recommendations 2016). Pure Appl Chem 88: 831-839.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi