Research Article, J Fashion Technol Textile Eng S Vol: 0 Issue: 4
Psychophysical Testing of Virtual Fabric Drape
Kalaoglu F1*, Buyukaslan E1 and Jevsnik S2
1Textile Engineering Department, Istanbul Technical University, Istanbul/Turkey
2Faculty of Technology, University of Banja Luka, Republic of Srpska
*Corresponding Author : Kalaoglu Fatma
Professor, Textile Engineering Department, Istanbul Technical University, Turkey
Tel: +90 212 2518808
Fax: +90 212 2518829
E-mail: kalaoglu@itu.edu.tr
Received: December 12, 2017 Accepted: February 28, 2018 Published: March 05, 2018
Citation: Kalaoglu F, Buyukaslan E, Jevsnik S (2018) Psychophysical Testing of Virtual Fabric Drape . J Fashion Technol Textile Eng S4:017. doi:10.4172/2329-9568.S4-017
Abstract
In this study, we tested five woven fabrics and observed their virtual drape behaviors. Fabrics’ mechanical properties were measured by Fabric Assurance by Simple Testing (FAST) system and simulations were created by O/Dev simulation software by Optitex. Drape behaviors of fabrics on a circular disc model were simulated and obtained virtual drape images were processed by image analysis software to calculate drape parameters. The purpose of this study is to understand the visual perception of people when looking at a fabric drape simulation. Which feature of drape is actually more significant to human eye? A psychophysical test was developed to understand human selectivity for drape geometry in virtual environment. Finally, 27 participants’ psychophysical test results were compared to calculated values. Participants found to be most sensitive to evenness and placement of folds while they were least sensitive to fold sizes.
Keywords: Virtual drape; Fabric simulation; Psychophysics; Drape geometry
Introduction
Fabric simulation is a complex phenomenon when compared to other materials simulation. Fabrics exhibit a non-linear, viscoelastic behavior even under very low forces which make the mathematical modelling behind simulation complicated [1]. Simulation of fabrics is very important for several industries such as animation, game and apparel. For apparel industry, fabric/garment simulations are particularly important from two perspectives: product development and online shopping [2]. Prototyping is a time consuming and expensive stage for product development. Sometimes three or four prototype is prepared before production to make sure that the garment meets the required aesthetic and physical fit. A realistic simulation may help manufacturers to minimize the number of prototypes. Online shopping is the other perspective where fabric/ garment simulation is outstanding [3]. Online apparel shopping is growing since 2000’s. However, consumers suffer that they cannot estimate how the garment will look and fit on their own body while purchasing in front of a computer screen [4]. Therefore, the main issue for online apparel shopping is the garment fit. A realistic garment fit simulation should meet the consumers requirements. Current studies concentrate on 3D scanning consumers and virtually dressing scanned images by simulation software to create a realistic experience. Consumer can observe the virtual garments on their own body model by some commercially available software. Optitex is one of the companies offering simulation software. This software enable users to insert fabric properties (such as bending rigidity, shear rigidity and extension) to create the most accurate and realistic simulations [5].
The main issue with simulations has been always the reality and accuracy so far [6,7]. However it is also important to understand what people see when they look at a virtual image. How sensitive they are to virtual stimuli where the stimuli are a virtual fabric? In this study, we aim to understand the visual selectivity of consumers to drape behavior of fabrics in virtual environment. In real context, fabric drape properties are generally measured by drapemeters [8]. Cusick’s drapemeter is one of the commercially available, easy to operate and inexpensive instruments [9]. In real drape meter testing, a circular fabric lay on a disc and drapes over it freely. In this study, we 3D modeled the disc of a drape meter by 3ds Max and virtually draped fabrics on the created disc model in O/Dev software by Optitex. Simulation images were saved and processed by image analysis software (ImageJ) to calculate virtual drape parameters. After quantitatively measuring virtual drape parameters we used a psychophysical test to understand consumers capability to distinguish drape behavior of virtual fabrics. As each measured drape parameter corresponds to a drape property (for example; drape coefficient, DC, corresponds to drape of the fabric. Lower DC values usually indicate a more drapery fabric), we tried to see if participants were successful to identify the variations of drape parameters.
Literature
“Drape” has been a long-term discussed phenomenon in textile researches as it directly effects fabric assessment and garment fit. Drape is the hanging behavior of a fabric under its own weight [10]. Another definition of drape is the orientation capability of textile material into eye pleasing folds under gravity [11]. Since “eye pleasing” is a subjective notion, researchers have developed a “drape meter” to measure drape properties objectively [9]. Drape coefficient (DC) is one of the significant parameter, which can be measured by drape meter, and gives an idea about the fabric drape behavior. However, DC is not enough to judge drape behavior of a fabric as two different fabrics might have same DC values. Therefore, additional drape parameters are required to understand drape behavior of fabrics deeply. Three items are important for drape geometry. These items are: drape area, fold number and fold shape [12]. Over time various drape parameters were suggested to measure geometry of drape. Some of these parameters are employed in this study. “Circularity” (CIRC) of drape is a parameter to establish proximity extent of drape shape to a circle [13]. Jevsnik and Zunic-Lojen used “angle between two neighboring peaks (α)” as a drape parameter [14]. In this study we calculated “standard deviation of angle between neighboring peaks (SD PA)” to assess evenness of fold placement. To best of our knowledge, governing SD PA as a drape parameter is new to literature. “Node severity” (NS) is a drape parameter to analyze fold sizes. It is the ratio of node height (wave height) to node width (wave length) [13]. Node height (NH) is radius from the center of supporting disk measured in centimeters and node width (NW) is the angle between neighboring peaks [15]. “Mean node severity” (MNS) is used for measuring node size of the overall drape profile. Each node has a different size and their size variation gives an idea about the uniformity of the nodes in a drape profile. A larger variation indicates non-uniformity of node sizes. Variability of node severity was initially used by Robson and Long and determined by standard deviation of node severity [13].
Psychophysics is a science to understand human reaction to various stimuli. During a psychophysical testing, participants are exposed to a stimuli and their reaction is measured by several methods. Ranking is one of these methods [16]. Participants are asked to rank the samples in an order according to the dimension that’s being questioned. In this study, “images (pictures) of virtually draped fabrics were used as stimuli.
Method
A virtual disc (18 cm diameter, 2 mm thickness) was initially created by 3ds Max software. The virtual disc was a simulation of Cusick drape meter’s disc. The simulation file was opened by O/Dev 3D garment simulation software. The created disc was used as pedestal while simulating drape of fabrics.
Five different woven fabrics were used in this study to observe their virtual drape behavior. Selected fabrics weights ranged between 168 to 215 g/m2 , four of them were 2/1 twill weave cotton and cotton blend fabrics while one of them was 100% wool fishbone weave fabric. The selected fabrics were quite similar in weight, weave and thickness. The reason of doing so was that participants are expected to easily distinguish drape differences of very different fabrics. However it is critical to understand the selectivity of individuals for similar fabrics.
After selecting fabrics, mechanical properties of them were necessary to create virtual fabrics in O/Dev software. Therefore, Fabric Assurance by Simple Testing (FAST) was used for measurement [17]. FAST involves a set of instruments to measure tensile, compression, bending properties of fabrics. Measured mechanical properties were converted to O/Dev validated units by “fabric editor” tool available in the software.
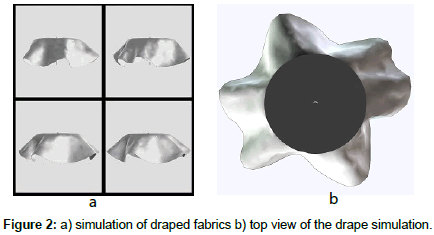
To create fabric simulation, 36 cm diameter circular patterns were prepared in 2D pattern design system (PDS) module of O/Dev. After inserting O/Dev validated mechanical properties of the fabrics to the software, fabric simulations were achieved on virtual disc shown in Figure 1. The simulation parameters were kept as default offered by the software (size of time steps: 0,02 and number of time steps: 10). The simulated drape images were saved from 5 different views (front, back, left, right and top).
As mentioned in literature, there are many different drape parameters to identify drape behavior of fabrics. Drape parameters used in this study and what they actually represent are given in Table 1.
| Drape Shape Parameter | Components of Shape Parameters |
|---|---|
| Area | Drape Coefficient (DC) |
| Circularity of the draped sample (CIRC) | |
| Number of Nodes | Number of nodes(NN) |
| Node shapes | Average fold size (Mean node severity, MNS) |
| Similarity of folds (Standard deviation of node severity, SDNS) |
|
| Placement of folds (Standard deviation of peak angles, SDPA) |
Table 1: Drape parameters used in the study.
The drape parameters of simulations were calculated by considering the “top view” as actual drape parameter tests also consider the 2D view of the drape to measure properties. Image analysis is a useful way to calculate drape parameters [13,18]. “Image J” is an open access software to analyze images and it was used in this study. The drape parameters in Table 1 were calculated according to literature [12-15].
After calculating drape parameters of virtual fabrics, we showed fabric drape simulations to 27 participants. Participants were the volunteers from college (students, professionals) and their ages were between 18 to 65. Only female participants were asked to attend the study as gender is thought to be a significant factor for psychophysical testing.
The virtual stimulis were the simulation images of five virtual fabrics from five different views as demonstrated in Figure 2. A questionnaire was developed for this research study. The questions included a definition of drape parameters. For example we explained what “similarity of folds” to participants with presenting them below paragraph. Similarity of folds” is the comparison of fold shapes for each image. There occur several folds on a fabric sample when fabric hangs freely. The shapes and the sizes of these folds may vary. Similarity of folds is said to be high when the fold sizes and fold shapes are similar.
After the description, participants are asked to rank samples according to “fold similarity” from 1 to 5. “1” meant to be the “minimum similarity of the folds” while “5” was the “maximum similarity”. The test involved 6 questions similarly to cover each drape parameter (see Table 1). Finally calculated drape parameters of simulation were compared to the ranking of participants.
Results and Discussion
FAST measured mechanical properties of test fabrics are given in Table 2. Calculated drape parameters of simulations, are given in Table 3. Participants answers to psychophysical test were analyzed by descriptive statistics. True rank order of each parameter was determined according to Table 3.
| Fabric | Bending Rigidity (B) (µNm) | Shear Rigidity (G) (N/m) |
Extension (E5) (%) | Thickness (mm) |
|||
|---|---|---|---|---|---|---|---|
| Warp | Weft | Warp | Weft | ||||
| A | 1,70 | 0,64 | 40,11 | 0,23 | 0,60 | 0,54 | |
| B | 2,54 | 1,75 | 115,31 | 0,60 | 0,66 | 0,60 | |
| C | 1,55 | 1,98 | 78,51 | 0,33 | 0,53 | 0,60 | |
| D | 10,6 | 1,76 | 238,06 | 0,23 | 0,53 | 0,80 | |
| E | 1,15 | 0,64 | 19,07 | 0,73 | 1,33 | 0,60 | |
Table 2: FAST measurements of test fabrics.
| Fabric | Number of Nodes | Circularity (no unit) | DC (%) | MNS (no unit) | SD of NS (no unit) | SD of Peak Angles |
|---|---|---|---|---|---|---|
| A | 6 | 0,65 | 0,49 | 3,55 | 1,63 | 16,47 |
| B | 6 | 0,50 | 0,39 | 3,57 | 1,62 | 20,33 |
| C | 7 | 0,44 | 0,30 | 3,22 | 1,05 | 13,51 |
| D | 6 | 0,73 | 0,57 | 3,47 | 1,59 | 21,40 |
| E | 9 | 0,55 | 0,45 | 4,45 | 1,02 | 5,81 |
Table 3: Calculated drape parameters of test fabrics.
Table 4 was developed to show the results of psychophysical testing of participants. To clarify the reading of the table, the bottom line of the table mentions the true ranking of the samples which was ranked according to calculated drape parameters listed in Table 3. For example, Fabric C circularity ranking order should be “1” (least circular) (see Table 3, third column). However only 11% of the participants answered correctly (highlighted numbers in Table 4 represents the % percentage of participants which ranked correctly). According to Table 4, 55% of the participants ranked circularity of A correctly; 30% of the participants ranked B correctly; 11 % of the participants ranked C correctly; 37 % of the participants ranked D correctly; 22 % of the participants ranked E correctly. If we calculate the correct ranking percentage, we conclude that success rate for ranking circularity is 31 % average.
| Circularity | Drapery | Average fold size | Similarity of folds | Placement of folds | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Participant Ranking | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| % of participants | A | 4* | 4 | 30 | 55 | 7 | 29 | 48 | 15 | 8 | - | - | 4 | 15 | 51 | 30 | 7 | 15 | 48 | 30 | - | 7 | 7 | 52 | 30 | 4 |
| B | 48 | 30 | 18 | - | 4 | 11 | 11 | 70 | 4 | 4 | 8 | 15 | 66 | 7 | 4 | 70 | 26 | 4 | - | - | 75 | 18 | 7 | - | - | |
| C | 11 | 47 | 8 | 34 | - | - | 4 | 4 | 81 | 11 | 33 | 59 | - | 8 | - | - | 18 | 15 | 67 | - | - | 12 | 18 | 70 | - | |
| D | 15 | 15 | 22 | 11 | 37 | 56 | 37 | 7 | - | - | - | - | 4 | 30 | 66 | 22 | 41 | 33 | 4 | - | 18 | 59 | 22 | - | - | |
| E | 22 | 4 | 22 | - | 52 | 4 | - | 4 | 7 | 85 | 59 | 22 | 15 | 4 | - | - | - | - | - | 100 | - | 4 | - | - | 96 | |
| True Rank Order | C | B | E | A | D | D | A | E | B | C | C | D | A | B | E | B | A | D | C | E | D | B | A | C | E | |
Table 4: Psychophysical test results.
Drapery of samples was ranked according to DC value in Table 3. Accordingly true drapery orders of fabrics are: C is the most drapery fabric while D is the least drapery. When we read all the values in the Table 4 for drapery, 48% of the participants ranked A correctly; 4% of the participants ranked B correctly; 11 % of the participants ranked C correctly; 56 % of the participants ranked D correctly; 4 % of the participants ranked E correctly. If we calculate the correct ranking percentage, we conclude that success rate for ranking drapery is 25 % average.
Mean node severity value in Table 3 corresponded to the average fold size. Accordingly fabric E has the highest average fold size (rank order 5) while Fabric C has the smallest average fold size (rank order 1). When we read all the values in the Table 4 for average fold size, 4% of the participants ranked A correctly; 7% of the participants ranked B correctly; 33 % of the participants ranked C correctly; 4 % of the participants ranked D correctly; none of the participants ranked E correctly. If we calculate the correct ranking percentage, we conclude that success rate for ranking average fold size is 10 % average.
Standard deviation of mean node severity (SD of MNS) value in Table 3 corresponded to the similarity of folds. The smallest standard deviation value meant that the fabric is more even in terms of fold shapes. Accordingly fabric E has the highest similarity of folds (rank order 5) while Fabric B has the least similarity of folds (rank order 1). When we read all the values in the table for similarity of folds, 15% of the participants ranked A correctly; 70% of the participants ranked B correctly; 67 % of the participants ranked C correctly; 33 % of the participants ranked D correctly and all of the participants ranked E correctly. If we calculate the correct ranking percentage, we conclude that success rate for ranking similarity of folds is 57% average.
Finally, standard deviation of peak angles (SD of PA) value in Table 3 corresponded to the placement of folds. The smallest standard deviation value meant that the fabric folds were evenly distributed along the perimeter. Accordingly, fabric E has the most even placement (rank order 5) while Fabric D has the most uneven placement of folds (rank order 1). When we read all the values in the Table 4 for placement of folds, 52 % of the participants ranked A correctly; 18% of the participants ranked B correctly; 70% of the participants ranked C correctly; 18% of the participants ranked D correctly and 96% the participants ranked E correctly. If we calculate the correct ranking percentage, we conclude that success rate for ranking of placement of folds is 51% average.
Conclusion
In this study, fabric drape simulation images were used as stimuli and participants’ capability to capture variations of drape features were analyzed psychophysically. Participants’ success rate for ranking circularity, drapery, average fold size, similarity of folds and placements of folds were 31, 25, 10, 57 and 51% respectively. As similarity of folds and placements of folds are a function of “evenness analysis of a shape”, results indicate that subjects are more sensitive to the changes regarding evenness. However, they were not very sensitive fold sizes. Surprisingly the subjects were not very selective of drapery differences. Nevertheless, it should be noted that the drapery was only considered according to DC values in Table 3. However it is a fact that different fabrics might have same DC values. Therefore, DC value may not be enough to justify the drapery ranking of samples. Finally, subjects were somewhat sensitive to distinguish circularity of fabrics. This study was done by only considering five woven fabrics, however more fabrics and more participants might give more reliable results. The participants’ demographic differences might be also considered for further studies.
References
- Hearle JWS, Amirbayat J (1986) Analysis of drape by means of dimensionless groups. Text Res J 56: 727-733.
- Magnenat Thalmann N (2010) Modeling and Simulating bodies and garments.
- Fontana M, Rizzi C, Cugini U (2005) 3D virtual apparel design for industrial application. Comput Des 37: 609-622.
- Kim DE, LaBat K (2013) Consumer experience in using 3D virtual garment simulation technology. J Text Inst 104: 819-829.
- Optitex (2017) O/DEV - Design, visualize & perfect; in a single 2D/3D environment.
- Song HK, Ashdown SP (2015) Investigation of the validity of 3D virtual fitting for pants. Cloth Text Res J 33: 314-330.
- Yan WYC (2011) An investigation on the reliability of 3d clothing simulation for garment fit evaluation.
- Sanad RA, Cassidy T (2015) Fabric objective measurement and drape. Text Prog 47: 317-406.
- Cusick GE (1968) 21-The measurement of Fabric drape. J Text Inst 59: 253-260.
- Peirce FT (1930) 26-The handle of cloth as a measurable quantity. J Text Inst Trans 21: T377-T416.
- Chu CC, Cummings CL, Teixeira NA (1950) Mechanics of Elastic Performance of Textile Materials: Part V: A Study of the Factors Affecting the Drape of Fabrics--The Development of a Drape Meter. Text Res J 20: 539-548.
- Chu CC, Platt MM, Hamburger WJ (1960) Investigation of the factors affecting the drapeability of fabrics. Text Res J 30: 66-67.
- Robson D, Long CC (2000) Drape analysis using imaging techniques. Cloth Text Res J 18: 1-8.
- ŽuniÄ Lojen D, Jevšnik S (2007) Some aspects of fabric drape. Fibres Text East Eur 15: 39-45.
- Sanad R, Cassidy T, Cheung V (2012) Fabric and garment drape measurement - Part 1. J Fiber Bioeng Informatics 5: 341-358.
- Manning SA (1967) Classical psychophysics and scaling.
- De Boos A, David Tester (1994) SiroFAST Fabric Assurance by Simple Testing.
- Schneider CA, Rasband WS, Eliceiri KW (2012) NIH Image to Image J: 25 years of image analysis. Nat Methods 9: 671-675.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi