Research Article, J Fashion Technol Textile Eng Vol: 6 Issue: 1

Regularities in Variation of Support Functions of Physically Nonlinear Elastic-Visco-Plastic Law of Strain of Cotton Yarn

Sultanov KS^1*, Ismоilova SI¹ and Mamatova NR²

¹Institute of Mechanics and Seismic Stability of Structures of the Academy of Sciences of the Republic of Uzbekistan

²Tashkent Institute of Textile and Light Industry, Uzbekistan

*Corresponding Author : Karim Sultanovich Sultanov
Institute of Mechanics and Seismic Stability of Structures of the Academy of Sciences of the Republic of Uzbekistan, Durmon yuli,31, Tashkent, 100125, Uzbekistan
Tel: +(871) 262-71-32
Fax: (871) 262-71-52
E-mail: sultanov.karim@mail.ru; sultanov.karim@gmail.com

Received: December 26, 2017 Accepted: February 09, 2018 Published: February 09, 2018

Citation: Sultanov KS, Ismоilova SI, Mamatova NR (2018) Regularities in Variation of Support Functions of Physically Nonlinear Elastic-Visco-Plastic Law of Strain of Cotton Yarn. J Fashion Technol Textile Eng 6:1. doi:10.4172/2329-9568.1000166

Abstract

Keywords: Cotton yarn; Nonlinear law; Variable modulus of strain; Parameters of modulus change; Experiment; Yarn strength; Linear density of yarn

Problem Statement

On the basis of fundamental concepts [1-3] and principles of the mechanics of structurally unsteady bodies and media under strain [4-7], a physically nonlinear elastic-visco-plastic law of strain of cotton yarn under tension to breakage was proposed [8]. Taking into account the unloading, this law takes the following form.

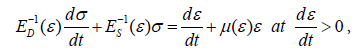(1)

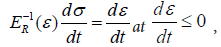(2)

where σ is a longitudinal tensile stress, t − a longitudinal strain of yarn, t − time.

A nonlinear function E_S(ε) a quasi-static modulus of strain under cotton yarn tension is defined. The methods for determining E_D(ε) a function of dynamic strain modulus, μ(ε) a function of viscosity parameter, E_R(ε) a function of unloading modulus are also considered [8]. Strain law (1) is developed on the basis of a linear viscoelastic model of a standard linear body.

It was shown in [8] that the nonlinear function of the change in modulus of cotton yarn strain E_S(ε) has the following parameters: E_N is an initial value at ε= ε_N=0; E_e is a minimum value at ε= ε_e; E_m is a maximum value at ε= ε_m; E_k is a critical value of the strain modulus at ε= ε_k at the moment of yarn breakage. Here a value of strain modulus in the interval [ε_m ε_k], denoted by E_S at ε= ε_S has also been introduced. The point is that strain modulus in the interval [ε_m ε_k], is not always decreasing. In some cases, after reaching the value E_m, with further rise in strain, the decline of E ceases, and remains approximately constant or increases. This moment at ε= ε_S and E = E_s is fixed as an additional point. Behind this point, the value of E either continues to decrease or remains constant, or increases.

Thus, the parameters of strain modulus E(ε) variation under yarn tension to breakage are E_N, E_e, E_m, E_S, E_k,ε_N, ε_e, ε_m, ε_S, ε_k. The values of these parameters depend on linear density of cotton yarn as the results of experiments show [8]. The aim of this work is to determine the dependence of these parameters on linear density of cotton yarn.

Determination of the Parameters of Strain Modulus

Experiments on cotton yarn tension to breakage were carried out with the nominal linear densities: T=14.0 (2); 15.4 (2); 16.5 (2); 18.5 (5); 29.0 (16); 50.0 (10); 72.0 (4); 100.0 (3); 160.0 (1) tex [8]. The number of spools with given linear density is indicated in parentheses. A total of 45 spools were produced. Before the test, as noted in [8], linear density of the yarn for each spool was determined separately [8]. As a result, actual linear densities of the yarn in each of the 45 spools [8] were obtained, which are given below.

For given nominal density T=14.0 tex: 14.56 and 14.6 tex; for T=15.4 tex: 14.7 and 15.0 tex; for T=16.5 tex: 16.7 and 16.9 tex; for T=18.5 tex: 17.73; 18.41; 18.6; 19.2 and 20.2 tex; for T=29.0 tex: 27.7; 28.10; 28.30; 28.50; 28.52; 28.61; 28.63; 28.7; 28.96; 29.03; 29.1; 29.27; 29.4; 29.5; 29.56 and 31.3 tex; for T=50.0 tex: 48.18; 48.2; 48.54; 49.10; 49.16; 49.32; 49.8; 50.03; 50.02 and 50.7 tex; for T=72.0 tex: 70.68; 71.41; 71.21 and 71.42 tex; for T=100.0 tex: 97.36; 97.4; 102.76 tex and T=162.13 tex.

Cotton yarns from each spool were tested on the «Statimat C» device consistently for 50 times, i.e. the experiment is repeated for 50 times. Then, the obtained 50 dependences of tensile force F (�?Ð) versus strain ε (%) are averaged by the software installed in the device. From the obtained average dependence F(ε) we determine the change in strain modulus E(ε) by the method described [8]. From each dependence E(ε) (total number of dependences E(ε) is 45), the values of parameters E_N, E_e, E_m, E_S, E_k in MPa and ε_e, ε_m, ε_S, ε_k in dimensionless form were determined according to the method described in [8]. The value of ε_N is taken equal to zero (ε_N=0).

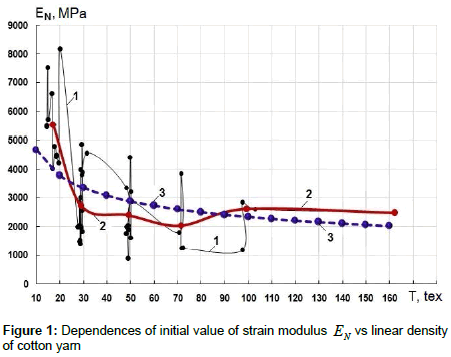
Figure 1 shows the changes in initial values of strain modulus E_N in MPa, depending on the actual linear density T in tex (1 tex = 10^��?5 N/m), based on experimental data (curve 1). Here, linear density of cotton yarn T corresponds to the actual measured value before the experiment for each yarn spool.

As seen from Figure 1, the change in actual initial values E_N at different actual values of T (curve 1) has a significant scattering.

The general trend of change in curve 1, Figure 1, is decreased with increased T. However, the very stochastic change in functions T and E_N (T) according to curve 1, Figure 1, could not be described analytically, so this curve was averaged over the nominal values of linear densities of cotton yarn. At the same time, close values of nominal linear densities were also combined into one group. As a result, the following six groups of linear densities were obtained.

The first group includes the yarns related to the nominal linear densities of T =14.0; 15.4; 16.5; 18.5 tex. The second group consists of yarns related to T =29.0 tex. The third group includes the yarns related to T =50.0 tex. The fourth group includes the yarns related to T =72.0 tex. The fifth group includes the yarns related to T =100.0 tex and the sixth group consists of yarns with T =160.0 tex. For each group, the values of linear density and the parameters E_N, E_e, E_m, E_S, E_k,, ε_N, ε_e, ε_m, ε_S and εk were also averaged.

Curve 2, Figure 1, was obtained using the averaged values of T and E_N for six groups. As seen from Figure 1 (curve 2), the change in mean values of E_N for T groups has already some explainable pattern of variation with increasing linear density of yarn. For small values of T, the initial value of strain modulus E_N is the greatest, and then the value of EN decreases with increasing T. At nominal values of T =100.0 and 162.0 tex, a slight increase in value E_N was observed. Now, curve 2, Figure 1, can be approximated by an analytic function. To do this, we choose a decreasing power function in the form

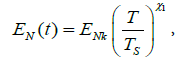(3)

Where E_Nk, T_S and , E_Nk, T_S and 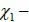are the coefficients of function (3), which must be determined. The ratio T/T_S is taken in order to have a dimensionless value in parenthesis in relationship (3). With the value of T_S = 50.0 tex, in most cases the values of dependence parameters E(ε) become steady or increasing.

The remaining two parameters of formula (3) E_Nk and χ₁ are determined by the method of least squares on a computer, and they are: E_Nk =2872.944 MPa and χ₁ = â�?�?0.302174. Here 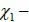is a dimensionless quantity. Curve 3, Figure 1, is constructed using formula (3).

The change in strain modulus E_N with increasing linear density of cotton yarn T, according to curve 3 (dotted curve), Figure 1, occurs monotonically, without any leaps. Thus, with certain transformations and averaging of curve 1 (Figure 1), obtained as a result of processing the results of the experiments, we obtain curve 3, which already indicates a certain pattern of change in the strain modulus E_N at different values of linear density of cotton yarn T.

With increasing linear density of cotton yarn T the value of strain modulus E_N gradually decreases. This statement, in general, does not contradict the results given in [1-3]. Using formula (3), it is possible to determine the value of strain modulus E_N for any value of linear density of the yarn obtained by pneumo-mechanical method of card system spinning.

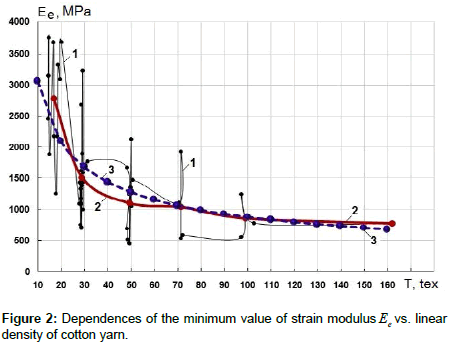
Figure 2 shows the change in the second parameter E(ε), of the minimum value of strain modulus E_e, in MPa, depending on linear density of cotton yarn.

Here, as in Figure 1, curve 1 – is a variation in actual values of E_e depending on actual values of linear density of the yarn T. Curve 2 – is a variation in averaged values of E_e depending on average values of actual values of T. As seen from Figure 2 (curve 2), the value of E_e with increasing linear density of the yarn sharply decreases to the value of T_S = 50,0 tex, while at T>50.0 tex its decrease is not so intensive.

Approximate curve 2 (Figure 2) with power function in the form

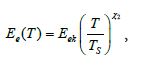(4)

The coefficients E_ek = 1274.765 Ð�?Pa and χ₂ = â�?�?0.544665 are determined by the method of least squares.

Curve 3, Figure 2, is constructed using formula (4). This curve is already a monotonically decreasing function of E_e , depending on the value of linear density of the yarn T.

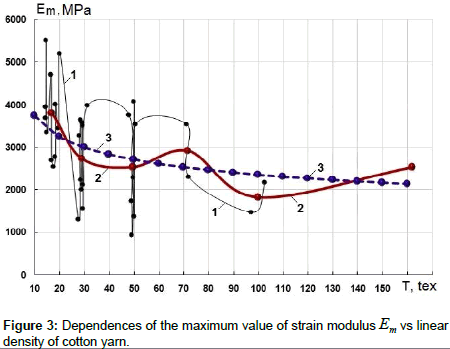
Figure 3 shows similar variations in the parameter of E_m − the maximum value of strain modulus of cotton yarn versus linear density of the yarn T.

Here, curve 1 is a variation in actual values of E_m, depending on actual values of linear density. Curve 2 is constructed from average values of E_m and T by groups of linear densities of yarn.

Variations in the maximum average value of strain modulus E_m, depending on averaged values of linear density of the yarn (curve 2, Figure 3), change in a more complicated way. To describe this curve, a power function is taken in the form

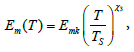(5)

Here, the values of coefficients E_mk =2705.089 Ð�?Pa and χ₃ = â�?�?0.202455 are determined by the method of least squares. Here, T_S =50.0 tex. At linear density from 10 tex to 160 tex, in 10 tex steps, the value of E_m is calculated and curve 3 is obtained according to formula (5) (Figure 3).

Curve 3 is actually an approximating curve 2 (Figure 3) and according to formula (5) the value of E_m as well as E_N and E_e (Figures 1 and 2) decreases monotonically with increasing linear density of yarn T.

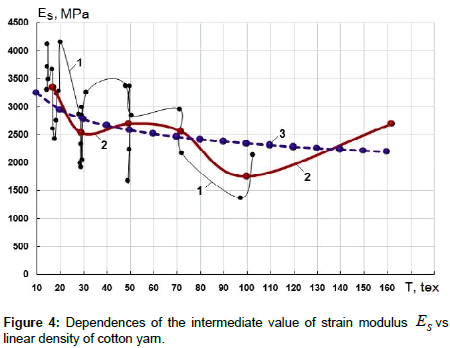
Figure 4 shows the variations in the actual (curve 1), averaged (curve 2) and approximating (curve 3) values of strain modulus E_S (intermediate between E_m and E_k), depending on the values of linear density of cotton yarn T.

Curve 3 is obtained with formula

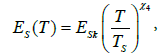(6)

where E_Sk = 2579.042 Ð�?Pa and χ₄ = â�?�?0.141952 both quantities are determined by the method of least squares using the averaged values of E_S and T by groups of linear densities.

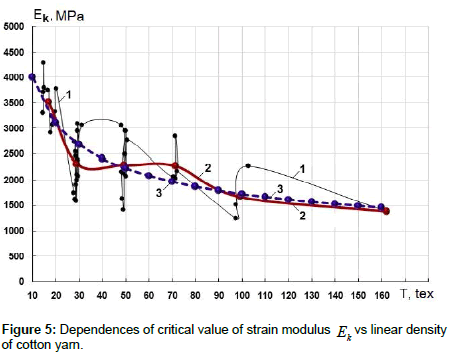
Figure 5 shows similar changes in the critical strain modulus E_k reached before the breakage of cotton yarn, depending on its linear density. Here, too, curve 1 is plotted by actual values of E_k and T, curve 2 is plotted by averaged values of E_k and T.

Curve 3 is obtained with formula

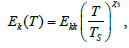(7)

The values of coefficients E_kk = 2222.351 Ð�?Pa and χ₅ = â�?�?0.365873 are determined using the least squares method. Here T_S=50.0 tex.

The nature of variations in actual, average and approximate curves E_k(T) (curves 1-3, Figure 5) is similar to the changes in E_N, E_e, E_m and E_S depending on the values of linear density of cotton yarn T.

Thus, the change in the parameters of functions of strain modulus E(ε), initial modulus , E_N minimum modulus E_e, maximum modulus E_m, intermediate modulus E_S and critical modulus E_k are determined on the basis of the results of processing experiments on cotton yarn tension to breakage [8].

The nature of the change in functions E_N(T), E_e(T), E_m(T), E_S(T) and E_k(T) according to Figures 1-5 is approximately the same: they generally decrease with increasing linear density of cotton yarn.

Formulas (3)-(7) allow us to determine by calculation the values of E_N, E_e, E_m, E_S and E_k for any values of linear density of yarn T. The obtained values of strain modulus E_N, E_e, E_m, E_S and E_k correspond to a certain average value of these modules for cotton yarns with linear density T of the card system produced by pneumo-mechanical spinning. For other systems and spinning methods, these parameters must be determined from the results of corresponding experiments on yarn tension to breakage.

Determination of Strain Parameters

Strain parameters of the function of modulus change E(ε), are ε_N, ε_e, ε_m, ε_S and ε_k Initial value of strain modulus of cotton yarn E_N from dependence E(ε), obtained from experimental results, was determined at ε_N =0.00025, i.e. very close to zero. Therefore, the value of ε_N in all cases is assumed to be zero, i.e. ε_N=0. In fact, E_N is a strain modulus of non-deformable cotton yarn at ε_N=0 But the value of E_N at ε_N=0 cannot be determined. Therefore, in the determination of modulus E_N, the strain value is taken very close to zero. Consider the change in remaining strain parameters of dependence E(ε), versus linear density of cotton yarn.

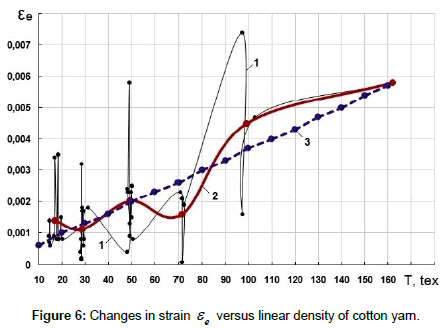
Figure 6 shows the dependence of ε_e,when strain modulus E reaches the value of E_e, on linear density of cotton yarn. Here, curve 1 is plotted according to actual values ε_e and T, i.e. it shows an actual change in parameter ε_e from the actual values of linear density of the yarn used in experiments.

As seen from Figure 6, the change in curve 1 is chaotic and does not yield to any analytical description. Having the average values of ε_e and T by groups of linear densities of cotton yarn, curve 2 is obtained. From the character of curve 2, it can be stated that with increasing linear density of yarn, the value of εe tends to increase. It is possible to analytically describe curve 2 by a more complicated function. However, for simplicity, it is approximated by a linear function in the form

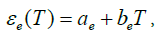(8)

where a_e=0.000321; b_e=0.000034 tex^��?1, determined by the method of least squares on the basis of dependence (8). Straight line 3 in Figure 6 is constructed using formula (8), setting a value of T from zero to 160 tex, in 10 tex steps. As seen from Figure 6, line 3 is actually the average straight line for curve 2.

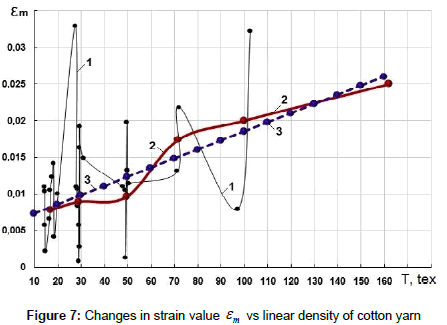
Figure 7 shows the changes in strain parameter ε_m, at which strain modulus of the yarn E reaches its maximum value E_m, depending on the values of linear density of cotton yarn T.

Here, too, curve 1 is an actual change of ε_m versus actual value of T. Curve 2 is the change in average values of ε_m and T by groups of linear densities.

Curve 3 in Figure 7 is an approximation of curve 2, just as in the previous case, by a straight line in the form

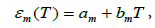(9)

where a_m=0.006054; b_m=0.000125 tex^â�?�?1 – are the coefficients whose values are determined by the method of least squares.

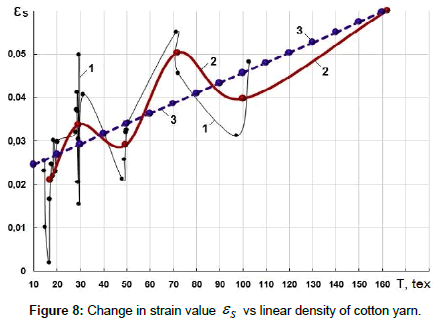
Figure 8 shows the dependencies ε_S(T) obtained by processing the results of experiments.

Curve 1 is obtained on the basis of actual values ε_S with actual values of linear densities.

Curve 2 is constructed on the basis of average values ε_S and T by groups of linear densities. Curve 3 in Figure 8 is an approximation of curve 2, just as in the previous case, by a straight line in the form

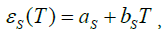(10)

Where a_S=0.022211; b_S=0.000235 tex^â�?�?1 – are the coefficients determined using the least squares method.

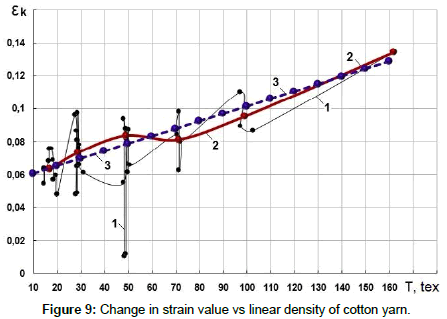
The change in critical value of strain ε_k at the moment of cotton yarn breakage versus linear density of the yarn is shown in Figure 9.

Here, too, curve 1 describes the change in critical strain ε_k versus actual linear density of the yarn. As seen from Figure 9, this curve also changes in a complex, stochastic manner.

Curve 2 in Figure 9 is constructed from the average data values of ε_k and T by groups of linear densities.

Certain regularity is already observed in the character of the change in curve 2 (Figure 9). This curve is also approximated by a linear function in the form

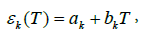(11)

where the values of a_k and b_k are determined by the method of least squares and they are: a_k = 0.056204; b_k = 0.000453 tex^��?1.

As seen from Figure 9, the straight line 3, constructed according to formula (11), describes the curve 2 with satisfactory accuracy. The value of critical strain ε_k, for cotton yarn with certain linear density is considered constant. For different values of linear density the values of εk are determined using formula (11).

Thus, the specific values of the parameters of functions E(ε)- E_N, E_e, E_m, E_S, E_k,, ε_N, ε_e, ε_m, ε_S and ε_k (ε_N=0), for specific values of linear densities of cotton yarn T, are determined from equations (3) - (11). With known values of these parameters, according to the procedure given [8], the change in strain modulus for cotton yarn with specific linear density T, is approximated versus the values of longitudinal strain ε under yarn tension to breakage.

As was noted above, equations (3) - (11) are valid only for cotton yarn of a carded spinning system produced on a pneumo-mechanical spinning machine from medium-fiber cotton of the 1st grade, of the 1st group of maturity, of the 4th type of fiber [8]. For yarns obtained by other technological methods and from other types of cotton, the values of function parameters E(ε) and equations (3) - (11) should be re-established according to the results of experiments on stretching these yarns to breakage and from the results of their processing.

The physically nonlinear elastic-viscoplastic law (1) [8], describing the process of strain of cotton yarn to breakage, includes functional parameters E_S(ε), E_D(ε and μ(ε). The function of quasistatic change of cotton yarn strain modulus ES(ε) includes nine parameters E_N, E_e, E_m, E_S, E_k,, ε_N, ε_e, ε_m, ε_S and ε_k. The values of these parameters are determined from equations (3) - (11). The function of dynamic strain modulus E_D(ε) is determined through the relation E_D(ε)=γ E_S(ε). As stated in [8], value of γ , for cotton yarn varies from 1.1 to 4. The current value of γ , the function of viscosity parameter μ(ε) and the unloading function E_R(ε) were determined from the relations proposed [8]. The unloading functions must be determined from the results of the corresponding experiments.

Thus, all functional parameters of the nonlinear law (1) and (2) become approximately known. This allows us to use the proposed law in applied problems of mechanics of yarns and in evaluating and predicting the strength of cotton yarn.

Conclusion

1. Based on the analysis of processing results of experiments on cotton yarn stretching, functional changes in the parameters of quasistatic modulus of yarn strain E_S(ε) are determined versus the values of linear density of cotton yarn.

2. The proposed functional relationships describing the changes in parameters ES(ε) make it possible to determine the values of these parameters E_N, E_e, E_m, E_S, E_k, ε_N, ε_e, ε_m, ε_S and ε_k depending on linear density of cotton yarn. This makes it possible to use the proposed nonlinear law of cotton yarn strain in applied problems of mechanics of textile yarns and threads.

3. Based on the proposed methods, it is possible to determine the functional parameters of the proposed nonlinear law for various types of yarns and textile threads and to assess the applicability of the proposed law under tension of these materials; this is a challenge for the future.

Funding

This work was funded by the Fund for Support of Fundamental Research of the Academy of Sciences of the Republic of Uzbekistan (FPFI AS RUz), Grants F.12-12 and F.9-14.

References

1. Morton WE, Hearle JWS (2008) Physical properties of textile fibers. (4th Edtn), Woodhead Publishing Limited, UK.
2. Shcherbakov VP (2013) Applied and structural mechanics of fibrous materials.
3. Ilyushin AA (2004) Izbrannye trudy. Tom 2 (1946-1966) Plastichnost.
4. Sultanov KS(1998)A non - linear law of the deformation of soft soils. J. Applied Mathematics and Mechanics 62: 465-472.
5. Sultanov KS (2002)The Attenuation of Longitudinal Waves in Non - Linear Viscoelastic Media. J Appl Math Mech 66: 115-122.
6. Bakhodirov AA, Ismailova SI, Sultanov KS (2015) Dynamic Deformation of the Contact Layer When there is Shear Interaction Between a Body and the Soil. J Appl Math Mech 79: 587-595.
7. Ismailova SI, Sultanov KS (2015) Nonlinear Deformation Laws for Composite Threads in Extension. Mechanics of Solids 50: 578-590.
8. Sultanov KS, Ismailova SI (2017) Physical Nonlinear Elastic - Viscoplastic Law of Strain of Cotton Yarn under Tension to Breakage. J Fashion Technology & Textile Engineering S: 3.