Research Article, Jceit Vol: 9 Issue: 3

SiMAMT: An Interactive 3D Graphical Simulation Environment for StrategyBased Multi-Agent Multi-Team Systems

Michael Franklin^*

Department of Computing of Software Engineering, Kennesaw State University, Marietta, GA, USA

*Corresponding Author: Michael Franklin
Department of Computing of Software Engineering, Kennesaw State University, Marietta, GA, USA
Tel: +25-19224-06360
E-mail: mfranklin@trulyintegrated.com

Received: July 02, 2020 Accepted: July 21, 2020 Published: July 28, 2020

Citation: Franklin M (2020) SiMAMT: An Interactive 3D Graphical Simulation Environment for Strategy-Based Multi-Agent Multi-Team Systems. J Comput Eng Inf Technol 9:3. doi: 10.37532/jceit.2020.9(3).224

Abstract

Keywords: Artificial intelligence; Multi-agent systems; Strategy; Simulation

Introduction

When multi-agent scenarios move beyond singular, short- term goals and into the realm of multi-layered strategies the complexity quickly scales out of the practical [1]. Much of the research in multiagent systems revolves around single- goal systems where multiple agents each work independently to achieve the same goal [2]. This does not accurately model the real-world scenarios found in larger systems where each Column Break independent agent has their own initiatives but still works together to achieve team goals. The SiMAMT framework is designed to allow a hierarchical strategy structure that works at each level to enforce policies that work at that particular level. Each sub-level of the hierarchy then works at its’ particular level order while considering the orders filtered down from the higher level. In this manner, the entire structure incorporates a multi-level strategy without having to use a large, monolithic policy (these large policies arise from applying small-scale solutions to much larger problems). When policies are allowed to grow in scale with the number of agents and the complexity of the system, they become computationally too complex to be applied, recognized, and changed in interactivetime. Strategy- based systems utilize group policies to aggregate the policies of individuals into a larger team policy (which we refer to as a strategy). Each of these strategies can be grouped together into a larger strategy at the next level. The SiMAMT framework creates a system to setup, model, control, and analyze multi- level strategies such as these.

It has been shown that strategies offer significant performance enhancement to artificially intelligent agents, that strategies can be recognized in real-time when complexity is limited, and that AI’s utilizing strategy inference will outperform their originally superior opponents [3]. The entire SiMAMT system can be reviewed in the journal article in which it is explained in detail [4], but some relevant back- ground is provided here for context. Additional content on the development of the strategy inference engine can be reviewed in [5].

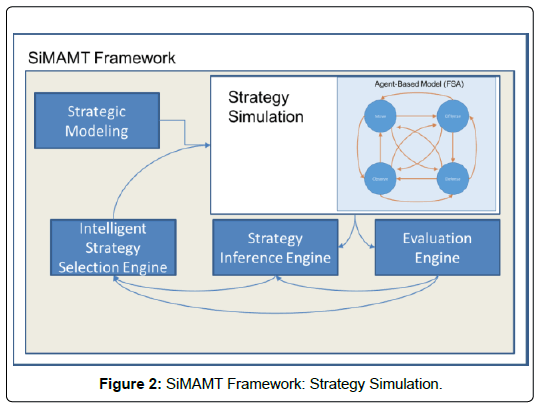
SiMAMT creates a realistic and complex environment in which the agents and teams of agents will act. The SiMAMT Framework is comprised of five distinct phases of processing in Figure 1, with the Strategy Simulation Module expanded. The first phase is the initialization phase called Strategic Modeling. SiMAMT is contingent on the ability to model strategy (i.e., to formulate complex systems of behavior into cohesive models). Once the models are in place the process commences with the Strategy Simulation module. This paper concerns itself with this module of the SiMAMT Framework. The simulation module produces data that is fed into the Strategy Inference Engine (SIE) for processing. Once this data is consolidated and processed it is moved forward to the Evaluation Engine where it is analyzed. This evaluation is then forwarded to the Intelligent Strategy Selection Engine (ISSE) where a final decision is made as to the current strategy that should be in place given the evaluation. The cycle then repeats as the simulation continues until termination. This framework provides high-fidelity modeling of real-world interactions at each hierarchical level according to individual policies, behaviors, and group strategies.

Related works

In the work of Anchez PS [6], the authors propose a multi-agent simulation system for modeling traffic and emission from traffic. Their approach is agent-based. This system is based on discrete events and models stations where vehicles can arrive, be serviced, and depart. This system is much simpler that the system proposed herein, and is typical of many well-received simulations extant today. Their system is fine for this application, but there are many simplifying assumptions made to keep the interaction limited and the number of agents low. There is also a reduced complexity to the overall system, such as agents of the same type having the same policy, or stations having similar policies. To accomplish the goals of increased, strategic complexity, our system offers individual agents, each with their own policy, comprising teams, which also have their overall group policy, Column Break that are part of an organized hierarchy with policies at each layer. Further, each of these policies can be changed during operation in reaction to real-time data analysis.

Similarly, in the work of Firdausiyah N [7], the authors are attempting to analyze traffic flow patterns in an effort to reduce emissions. They are also using multi-agent systems, and are having to take steps to reduce the overall complexity due to the inherently complex nature of multi-agent systems. However, these authors chose two additional steps that produce stronger results: first, they are using Adaptive Dynamic Programming (ADP) to attempt a more reactionary learning and adaption method; second, they are using Reinforcement Learning (RL) to learn from experience. These two methods move their solution closer to ours, but they are still using fixed policies with small adjustable parameters, and they are using the same policy generator for the same class of agent in their simulation. Our solution adapts in real-time, uses strategic thinking, and reacts to both teammates and enemy (again, our simulation is multi- team as well).

In a work that is similar to another application of the SiMAMT framework [5,8], the authors, Zhou Y [9] propose the use of a multiagent simulation to delve into the world of energy. Their work takes on peer-to-peer (P2P) energy sharing mechanisms. Their system uses multi-focal evaluations and heuristics to tune the policies of the agents to maximize energy sharing and reduce energy waste (or loss). Their approach is proof positive of the applications of multi-agent simulations within this context. However, their approach models the systems as cooperative, but does not model the environment or other energy reduction elements as adversarial teams. That is, they do not have intelligence modeling the counter effects, a hallmark of SiMAMT.

Though the context is different, the article from Treuille A [10] elucidates the increasing complexities of simulations that require interactive-time interactions amongst many disparate elements. Further, in [11] this idea is built upon and grown. The authors present several correlated instances where the simulation must simulate, detect, and adjust for multitudinous particles inter- acting in a variety of patterns, flows, and avoidances.

In the work of Laviers [12], the authors seek to make an alternative play based on reading the opponent’s previous formations and predicting their current play. If the current play they recognize is predicted to outperform their own play, they attempt to make the change to a better play in real-time. Their work is not multi-agent in that it considers the play itself and not the individual actions of the players, nor is its multi-team as they are only considering one team (namely, the opponent). Their procedure and overall idea are very well done and informative for our work.

This work provides a general background in both Game Theory and Decision Theory [13], specifically as it applies to multi-agent system [14]. It introduces Game Theory into multi-agent learning. These works give several approaches to solving multi- agent learning systems and their mathematical foundations. These reference works provide the underpinning of the work that will be introduced herein in multi-agent systems and large-scale game solutions.

There is much foundational work in both game theory and learning in multi-agent systems. Rather than review each of the multitudinous examples like [15,16 17] in this proposal, there is a larger work that summarizes each of these and compares them. Bowling, M [18] also firmly establishes this background while entrenching itself in the multi-agent learning scenario, and in particular in how the related work from game theory (e.g., the Nash equilibrium) fits into the more limiting field of multi-agent learning. This served as a check for the formulation of the stochastic game introduced in this research so that individual agents can exhibit behaviors that lead to the inference of their own behaviors, and subsequently lead to the inference of the team strategy. Without this mathematical foundation and exemplary work to stand on, this proposal would be weighed down with many more proofs and theorems. Instead, this work utilizes these wellformed ideas and builds on them.

An excellent treatise on team management, role assignment, and in-game communication can be found in [19]. This work gives good design principles and framework information on exactly the type of scenario envisioned by this proposal - multi-agent team coordinated behavior with both cooperative and adversarial elements. This paper provides much of the initial material for considering teamwork inside of the stochastic game presented in this proposal and in the communication sections of the multi-agent and strategy inference portions.

Strategy- based system specification (SIMAMT)

It utilizes a model-based approach to agent management, but the actual model is flexible. Previous iterations have used finite state machines and search tree implement. When the strategies, and their associated policies, can be derived (or provided) probabilistically then they can be represented as either Finite-State Automatons (FSAs) or Probabilistic Graphical Models (PGMs). These models can then be encapsulated in two ways: first, as diverse sets of graphs for each such policy where the relevant walks in the graph represent strategic action chains (representing policies); second, as multiple isomorphic graphs where the weighting of the edges encodes the decision process. This means that multiple agents interacting within the same environment can use strategies (with their related set of policies) to execute their actions and, thus, act intelligently. In this scenario, then, it is possible to reverse engineer this strategic interaction based on observations of the actions taken by a particular agent (this is the work of the SIE). By comparing the observed actions with the probable actions of each policy a belief network (BN) can be formed that leads the particular agent to predict the policy of another agent within the system. Combining the agent’s observations of policies inferred from the observation of other agent’s actions, the team leader can then infer the most likely strategy in play by the other teams in the scenario. In a system with increasing complexity, where calculating multiple factors may be time-prohibitive, the ability to match these candidate graphs (e.g., PGMs) with the currently forming belief network Column Break image (another graph) in real time can be challenging. As noted in [20], an approximate solution is available and can perform this matching in real-time.

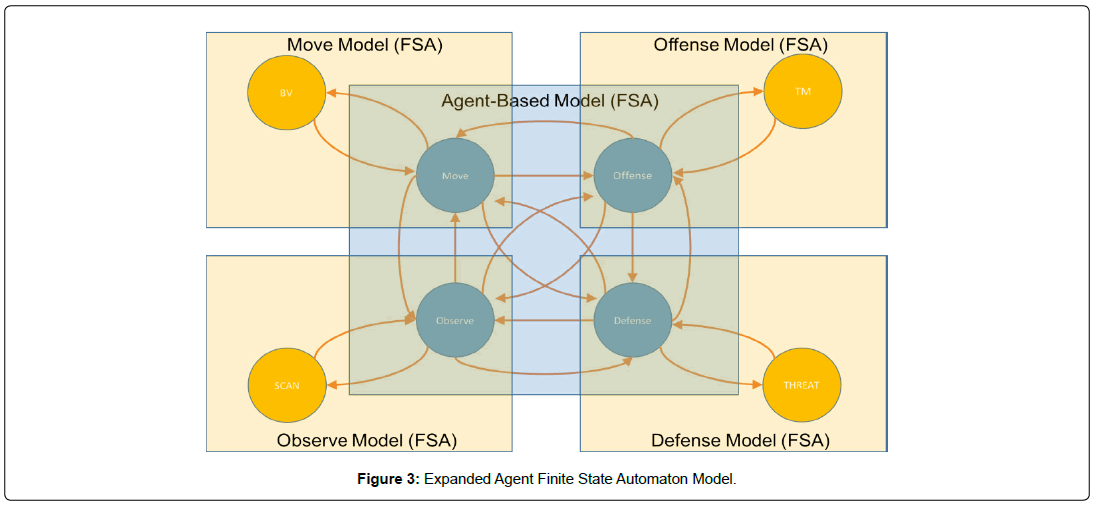
This work utilizes a FSA that allows for a similar action set for each agent but with customizable factoring (probabilistic progression through the model), shown in Figure 2. The distinct phases can be thought of as Markov random fields with multiple variables, reflecting real-world agents. The model progresses through the states (e.g., a move, a cover, a fire, or an observation phase). The weighting (factoring) of each agent action is probabilistically determined by the individual agent’s policy. This policy is given to them from the strategy the team is following. Thus, the agent considers their action with their own probability (based on their player type) which reflects their own ‘personality’. This probability is then modified by the policy according to the overall policy goals. Finally, the team strategy weighs in on the probability. This gives the effect of individualized performance with overall short- term goals and team performance with match-wide long-term goals. This is critical to the real-world performance of the simulation system: it must emphasize individualized activities but constrain them (or at least influence them) by the team’s overall goals (as realized in the team strategy).

In particular, the FSA will model the basic behaviors and their probabilistic pathing. In the FSA shown in Figure 3, the agent starts in the Idle position. They have a probability of making a move, seeking cover, and firing on the other team. They have a certainty of observation, both active (noting other agents in view) and passive (noticing zones from which they are receiving fire). These observations of the other agent’s positions, and, most notably, their transitions from position to position, are the key elements of the strategic inference during the simulation.

By way of example, let’s examine the inner-workings of a model utilized in a peak-shaving algorithm simulation or energy modeling. In this scenario, there are two teams. The first team is the campus. It is a hierarchical network of rooms, aggregated into sections, aggregated into floors, aggregated into buildings, aggregated into a campus. The second team is the population. They are a hierarchical network of people, aggregated into groups, aggregated into preferences, aggerated into years, aggregated into the population. These two teams are adversarial. The population is using energy, the campus is trying to save energy. The simulation allows for the preferences of each element, at each hierarchical level, to be expressed (i.e., modeled and simulated with variability within the set of agents). With this structure in mind, we can inspect one or two small elements within this simulation to see how they are motivated. A person has a set of preferences. These preferences are sliding values that can be assigned pseudo- randomly, statistically, or modeled as a distributed population.

Text Box Text Box (e.g., w.r.t. heating and cooling preferences, 20% prefer 3 degrees, 30% prefer 2 degrees, 40 % prefer 1 degree and 10% are neutral.) This means that during their Move phase they will determine if there is better environment nearby and move there or they will move to their next scheduled location (according to their individual customized policy). In their Offense (action) phase they will adjust the thermostat to suit their needs. During their Defense (adjust) phase, they will remove a jacket or pick up a blanket, for example. In their Observe phase they will take measurements of their surroundings and the time of day. Within each of these phases, there is a system that chooses the next or best action from the set of actions. This is accomplished using a probability analysis of the preferences matched to the simulated environment. The policies are modeled as FSA’s, as mentioned, and so the simulation moves them through their progression of states according the probabilistic pathing through the policy space as laid out in the FSA. Further, these policies are evaluated at each stage and can be swapped out with the next best policy according to the strategy being employed by the group. Next, viewed from the opposite side, the rooms are modeled similarly. Each room has it own characteristics, such as heat loss, exposure to sun, etc. Each room is simulated in response to the day as it progresses, the heat outside, the weather, etc. The simulation moves each room through its own progression, just as it does for every other agent. The room will use its Move phase to determine if it can move (it likely cannot). It will use the Offense (action) phase to manipulate any settings it controls, like lowering shades or opening a set of baffles. The Defense phase will be its reaction to the agent’s actions, like mitigating against the actions of the person in the room by column break limiting the adjustments or restricting controls (per its policy). Finally, the Observe mode is used to gather new information from the environment. This is a small example, but it should be emphasized that each policy is customized for every single agent and, while the steps are similar, the simulation will take customized actions for each of them.

Strategy simulation

Creating simulations for multi-agent multi-team interactions is a daunting task. It is non-trivial to compose a situation where each individual agent maintains their own ‘personality’ while still following the assigned policy dictated by a team’s central command. Further, the complexity is inflated by ensuring that each of these agent policies is coordinated into a cohesive team strategy. Finally, peaking the complexity, is evaluating the performance of the team’s strategy against other teams’ strategies in interactive time. This is the work of this research, proposing SiMAMT, the simulation space for multi-agent multi-team engagements, and testing it. We will first cover the system and how well it models the virtual environment for strategic interaction. Second, we will deliver results from a practical test of strategy inference within such an environment using the SIE (Strategy Inference Engine).

In multi-agent multi-team scenarios, teams of agents are often trying to use the observed actions of the other team’s agents to predict the behavior of the other team. Strategy inference in such environments assumes that there is some underlying strategy that these teams are following, that such strategies can be inferred through observed actions, and that they can counter such strategies in interactive time by selecting a superior strategy. These strategies may be modeled using various graph structures such as trees, finite state machines (FSMs), or probabilistic graphical models (PGMs). To best determine which strategy a team is following it is necessary to match prospective models representing observed behaviors or policies with known models (each of which represents previously learned strategies and their related policies). Matching these models is difficult when their progression is probabilistic, the models can be homeomorphic (one is a subgraph of the other) or isomorphic (the bijection is true (i.e., homeomorphic in both directions)), and there are a variety of factors weighting each branch of the tree [21]. Such intensive matching is taxing even on HPC systems, especially when interactive time decision making is key to the scenario. Further, the complexity of the multiple teams, each of which is running their own strategy, and multiple players, each of which is following a distinct policy customized for them by their strategy, make interactive time computation challenging. The results will show that the environment, which shall be of a satisfactorily complex nature, is successfully modeled as a multi-agent system (i.e., each agent following their own policy, each of these policies coordinated by a strategy at the team level) with multiple teams; further, the environment is able to be analyzed by the SIE, and that experiments verify both the execution of strategies and their recognition (inference). Finally, the experiments will show that this inference leads to interactive time decision making within the match.

It will be shown that strategies offer significant performance enhancement to artificially intelligent agents, that strategies can be recognized in interactive time when complexity is limited, and that AI’s utilizing strategy inference will outperform their originally superior opponents. In contrast, classical ma- chine learning requires repetitive trials and numerous iterations to begin to form a hypothesis as to the intended actions of a given agent. There are numerous methodologies employed in an attempt to reduce the number of examples needed to form a meaningful hypothesis. The challenge arises from the difficulty created by the diversity of possible scenarios in which the machine learning algorithm is placed. Given enough time and stability a machine learning algorithm can learn reasonably well in a fixed environment, but this does not replicate the real world very accurately. As a result, strategies offer an opportunity to encapsulate much of this policy-space in a compact representation. Strategies have to be learned as well, but the AI is learning smaller, individualized models rather than one large, monolithic policy. These models are also transmutable to another instance of a similar problem. Additionally, they can be pre-built and then modified to suit the exact situation. If these strategies are represented as graphs then they can be classified, categorized, identified, and matched. In particular, they can be represented as a variety of highly expressive graphs such as PGMs, FSMs with probabilistic progression, or other graph structures composed of complex elements. The SIE uses Column Break FSAs to build a belief network of candidate strategies from which it selects the most likely strategy an opposing agent is using. Once created, this research scales this to work at even larger scales and with higher complexity.

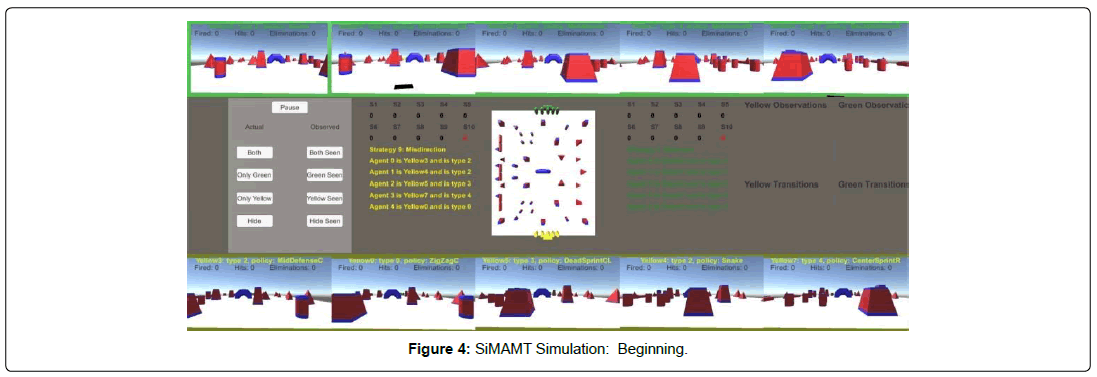
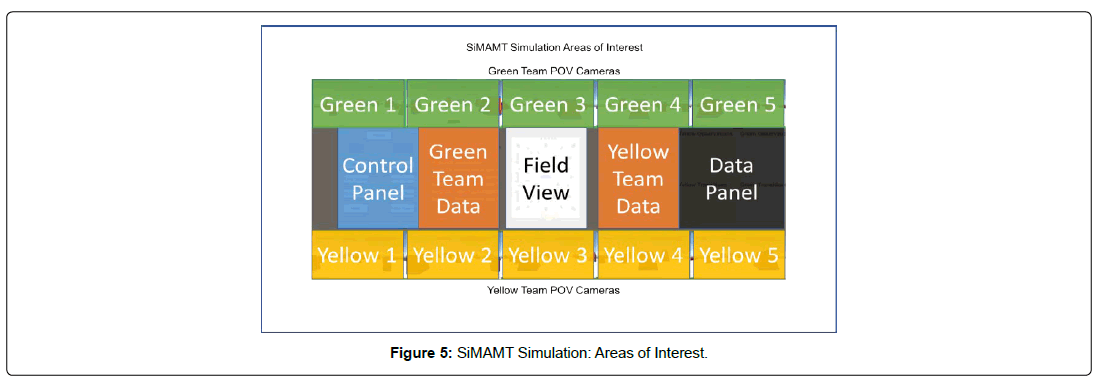
The main view of the Strategy Simulation module’s output, the simulation itself, can be seen in Figure 4. This view shows the POV cameras for each team, the control panel for the simulation, the team’s data panels, the simulation’s data panel, and the field view (Figure 5 shows the layout of these modules).

Through the Strategy Simulation module, SiMAMT is coordinating the individual agents, each of which has their own unique features (e.g., speed, armament, etc.). It then groups these agents into any number of teams, as requested by the simulation configuration. These teams, then, have a leader (e.g., coach, captain, etc.). This leader first selects which agents on its roster to make active, then assigns a role and a policy to each agent according to the strategy for the team. This means that the list of roles (i.e., types of behaviors in the simulation) is distinct from the agents. Since the team leader is assigning roles to the individual agents on their team then matching the right agent to the right role is imperative for success. This may be a good matching or a poor matching (this variability allows for unique combinations of teams, roles, and agents, and thus adds ‘role assignment’ to the list of elements the simulation is modeling). Further, the individual agent’s policy contains many variables about how the agent will act in the various game phases. This accomplishes the goal of maintaining individuality while imprinting each agent with their portion of the team plan. This could lead to individual agents breaking away from their orders and rebelling (where the agent’s personal desires overwhelm their policy-assigned behavior), or it could lead to an agent’s compliance (where the policy settings take precedence). This is an example of the many factors available for each agent, and reflective of the expressivity of the simulation (that claims to model complex strategic interaction between team members and between other teams). Additionally, the team leader has more policies available than players, so they can reassign, switch, or drop policies during the match. The leader is also responsible for evaluating the overall performance of the team and, ultimately, deciding if the team should switch to another strategy. This process is addressed in the SIE portion of the research.

The Strategy Simulation follows the model loaded for execution. This model is hierarchical in that it incorporates a model built of models. Each layer of the hierarchy corresponds to a layer of the execution model in the simulation - strategy models, policy models, etc. For example, consider Figure 2 that shows an expansion of the Strategy Simulation with a sample model. This model shows the procedure for simulating the action of a single agent in a particular scenario. The agent is initialized by assigning all of their characteristics to an agent created inside the simulation (this agent will have distinctive qualities from other similarly created agents because of the variety of the characteristics and control variables even though the model may be the same). Once initialized, the simulation starts the agent control loop. Depending on the desired functionality, these various steps, shown here in a cycle, can be done serially or in parallel. The robustness of the simulation is that it follows the models, so it can work either way. Regardless of the mode of execution, the various steps are examined as indicated by the model. In this example, the agent makes a determination about whether or not it should move, take an offensive action, make observations, and take any defensive actions. There are a variety of factors that go into each of these decisions, but the overall view is that the strategy has initiatives, realized through the policies’ behaviors, that direct the individual agent. The agent, however, has innate characteristics that determine how likely it is to obey the orders directly without question or to act as an autonomous agent. The simulation progresses each agent through this cycle and relays commands to the agents and receives observations from the agents to pass along to the SIE.

Additionally, SiMAMT can also enforce additional constraints in the simulation, such as not being able to shoot or observe when under cover. It can set maximums or minimums, control overall conditions (e.g., weather, duration, etc.), and observe the overall performance of each team, each agent, and the simulation itself. The simulation engine can handle any number of players, active players, field positions, policies, and strategies as long as the data files provided detail each of them.

The simulation environment is constructed from data files. The files contain all of the configurable data that describes each aspect of the simulation in detail. The simulation engine is designed so that the inner workings of the engine are held within the system specifically so that it can be easily adapted to new simulations. As illustrated previously in the model- based diagram for SiMAMT, Figure 2, the data files that configure the simulation are held in the Strategic Modeling portion of the framework. This section is separate from the execution-cycle elements of SiMAMT because it is the portion of the framework where the users can configure the models, parameters, and any other necessary configuration elements of the simulation. With the files configured and the scenario confirmed in the models, the framework then proceeds to the execution-cycle. Again, this portion of the framework utilizes those models that were input, so the inner workings of the framework do not have to be altered for simulation execution. Once all of the data is loaded that configures the framework, the agents are then recruited onto teams. Once fully configured, the simulation assigns strategies to each team. These strategies then match agents with agent types (e.g., commander, sniper, etc.) and assigns an initial policy to each. Each player’s policy then assigns them a particular behavior, complete with their movement diagram. Each player is then moved to their initial state (the home position on them movement diagram) and then the simulation begins.

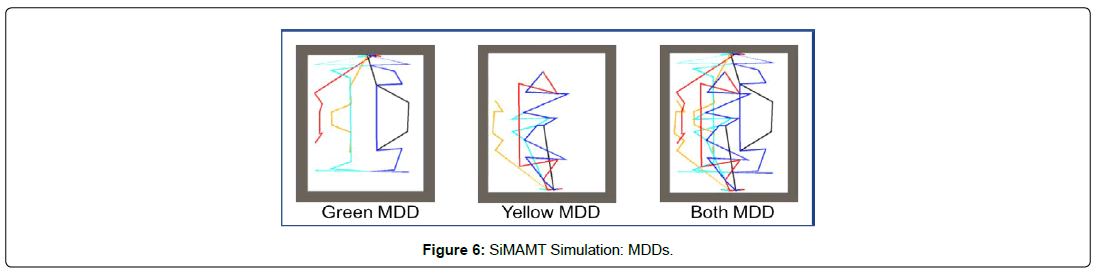
One critical element to understanding and deploying strategy within a simulated environment is the Movement Dependency Diagram (MDD). The MDD is a diagram that is the result of a search through the entire state space (in each sys) Column Break teem, states are defined by that system as locations, positions, or situations where an agent is located and from which they can take actions to shift their state). Generically, the state space of an environment is the list of connected states that are reachable through every possible action. In strategic simulations this is the entire list of movements - that is, any and every action that moves an agent from one position to another. This creates a diagram that shows all possible movements and all possible subsequent movements from those, thus creating a Total Movement Dependency Diagram. The Total Movement Dependency Diagram can be made into sub-graphs where each sub-graph contains a particular set of connected moves within the larger set of moves. These sub-graphs can then be tied to certain strategic behavior (e.g., playing a particular position in soccer).

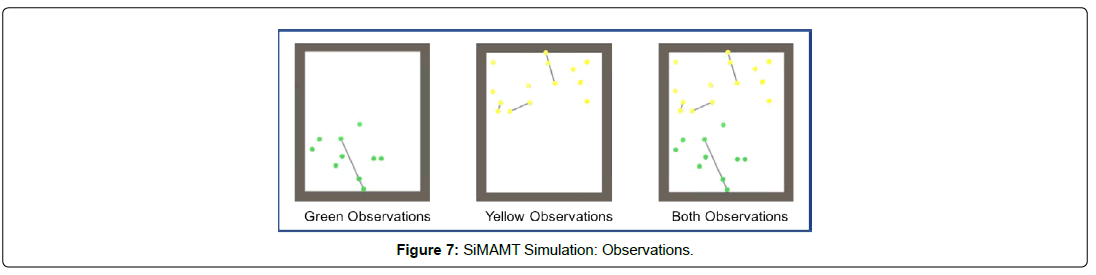
Figure 6 shows the aggregate MDD’s for the green team, the yellow team, and both teams. Each color represents the MDD for each team member. The sum total of these MDDs shows the team’s MDD, and, thus, their overall strategy being. This team MDD is a subset of the Total MDD. Correspondingly, as the simulation progresses and observations are being made the teams begin to formulate their best estimate of the other team’s MDD. This can be seen in the simulation progress images shown in Figure 7. This forms the basis of the Strategy Inference Engine’s Belief Network (matching these sub-graphs to the known set of strategy graphs). Each of these images are close-ups of the central screen of the simulation engine, the overhead view, shown previously in Figures 4 and 5.

The simulation is a discrete-time simulation where each agent (and each element of the environment) can both exe- cute and receive actions at each interval. This is an agent- based simulation (or, agent-model-based, to be more precise). Algorithm 1 is utilized in the execution of the simulation. As previously mentioned, the FSA for each agent makes decisions at each interval. Based on the FSA shown earlier Figure 8, the various sub-models are executed in the order needed (some steps can be skipped, done more than once, etc., depending on the model selected or the strategy in force). Using this sample FSA, each action can be considered in turn. First, the agent examines its behavior to determine the next move. This is done probabilistically based on the behavior (that lists each next move and its accompanying probability). Next, the probability of a move is based on the Movement feature of the strategy. If a move is issued, the agent proceeds to the next state at the speed dictated by the policy. It should be noted that the speed with which they move determines their vulnerability during the move and the ability to aim during the transition. This provides an added realism to the simulation that is sensible (e.g., if an agent sprints, they are less likely to be hit, but less likely to aim correctly). The next action for consideration is defense. The probability is based on the Aggression and Posture factors. Again, defense may choose cover, and under cover the agent is unlikely to be hit but is unable to fire or make active observations. The next probable action to consider is offense. This probability is based on the strategy factor of Aggression and Posture and metered by the agent type and policy. The next action to consider is observe. This involves the same basic flow as the firing phase, but they are only noting which agents are visible and noting any transitions. If they are being fired upon then these positions are inferred to contain other agents and are so noted (this uses an inverse kinematic to determine reverse trajectories based on those positions observable from this current position). This completes the action selection FSA for this agent and the simulation moves on to the next stage.

To better understand the strategy factors involves examining them in context. For example, in the 5-vs-5 speedball paintball scenario, the Aggression speaks to how the strategy might overwhelm the policy to force a player to move where they might not have otherwise. It may also overwhelm their choice to take cover. Likewise, the Movement factor controls how likely they are to move and also in which direction. For example, the players may start to retreat (move backwards through their move list) as the number of active players remaining on their team diminishes. The Distribution often overrides move probabilities to move players closer to each other or farther apart depending on this setting. The Posture factor controls fire aggression, movement aggression, and the agent’s likelihood to stand and fire vs. retreat. Finally, there is a Persistence factor that keeps the players on their current policy or freeze them to move to another policy. These factors, as well as the subset of policies, differentiate the strategies one from another. It is important to note that the complexity of this environment is possible even with each agent in the simulation following the same model (though with different probabilities). If the models varied, the SIE would be even more effective because the engine would have more diversity in the observations provided for inference. The simulation is comprised of a series of engines that drive in Figure 9.

Algorithm 1 Simulation Engine for Strategic Multi-Agent the action of the simulation forward. As the simulation runs it is gathering data and passing the data on to both the Evaluation Engine (EE) and the Strategy Inference Engine (SIE). The Evaluation Engine (EE) analyzes the policies in place for the team based on their strategy and decides if any players need to be assigned new policies for better performance. The SIE gathers data on what is being observed by the agents in the field and decides on the most likely policies and strategies being followed by the other teams in the system. Both of these engines produce output, and this output (i.e., their evaluation) is fed into the Intelligent Strategy Selection Engine (ISSE). The ISSE takes this evaluation data and analyzes it in comparison to the most likely strategies in play by other teams. It then decides if a change in strategy is warranted. The ISSE makes the final decisions on strategies in play, strategy comparisons, and strategy decisions.

Results

The experiments pit the same 16 players, placed on the same two teams (Red and Blue), against one another while varying the strategies that each team is using. A match is configured as two teams, 8 player max per team, 5 active players per team, and 1 - 3 hits to eliminate a player from the contest. As a result, even though the players do not change, they are assigned differing roles, differing overlying strategic factorizations, differing policies to follow, and each match is still probabilistically projected. There are nine available strategies comprised of a combination of the 26 policies used in this experiment.) For example, the Strong Defense strategy has two Heavies, two Riflemen, and one Commander. One heavy takes the back right defensive position and, as a heavy, will concentrate fire on the enemy while protecting its own team members. The heavies are not very mobile, so they make up for that fact with heavier fire rates. The two riflemen move rapidly to the front right and left position to set up the forward attacking position and spotting the flag. Finally, the commander oversees the battlefield and provides support to both of these pairs of players while keeping the team together. As a result, the commander stays more centrally located in the field but keeps under cover. Each of the strategies is formulated for such an effect (e.g., offense, defense, balanced, etc.).

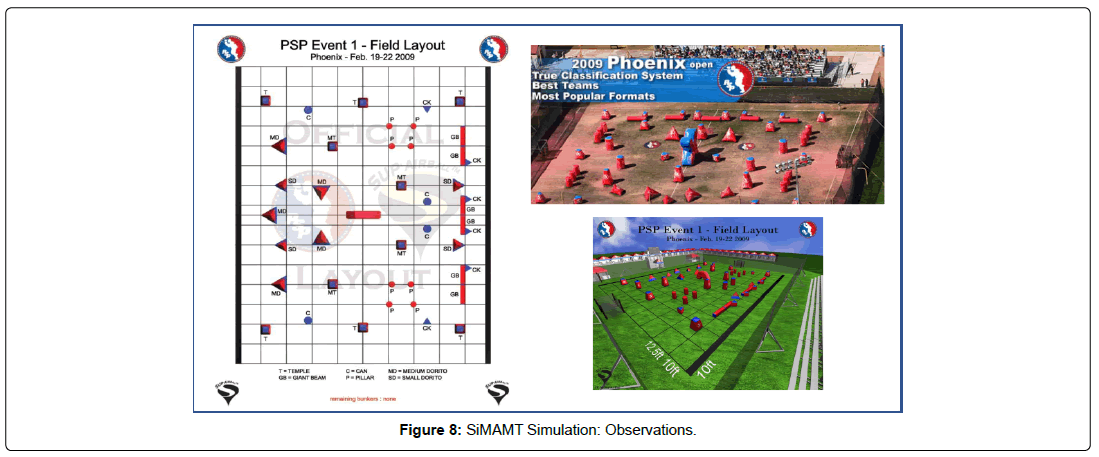
Each team has their own side with a number of obstacles of varying size, protection, and position. While both sides are similar, they are mirrors of each other, so there is a right- and left-hand portion to each side of the course. Figure 10 shows an official field diagram from the PSP Event held in Phoenix, AZ [22]. Additionally, it shows a television still frame of the actual field, and provides a 3D model of the same field. This field was then rendered in Unity as a 3D model with each obstacle created as a distinct object. The agents were then placed in this 3D environment at their default state (here, home base). The simulation then uses the underlying strategic models with their policies and behaviors to move the players through the field. In so doing, the agents form strategic formations and have a coordinated plan of attack. Additionally, they begin to gather observations and transitions about the agents on the other team and that is used in the strategy inference. The agents can also begin to eliminate agents from the other team as they observe them and fire paintballs at them. The simulation uses ray casting to determine which agents can be observed and which can be fired upon. As noted previously, the firing process is probabilistic and governed by the simulation variables, to their varying degrees of accuracy.

As an important note, even though the simulation engine is a multi-agent multi-team simulator with the particular application of 5-vs-5 speedball paintball, it could easily be converted to run any similar system with any number of teams, players, policies, or strategies.

Some additional settings in this particular simulation: no blindfiring (a player must see another player before it is allowed to fire), no stacking (no double-occupancy of any one side of a particular obstacle), and all match stats are tracked (e.g., the number of hits before elimination, size of each team, etc.).

There are a number of variables that affect the decisions made by the simulation engine as it progresses players through the simulation. First, the rate of fire is determined by the player and the player type. The fire probability is measured once per round fired. Second, the strategy factors of Distribution (how close the agents on a team stay to each other), Aggression (how likely the agents are to move or fire), and Posture (offensive, defensive, etc.) weigh in. Additionally, the policy itself speaks to the firing positions and lanes where the player can fire. Finally, there are a number of global simulation variables that determine if shots fired actually hit or affect the target (e.g., general accuracy of paintball guns, probability of breakage of the paintball, etc.). These provide a stronger level of realism for the simulation and demonstrate the flexibility and expressibility of the framework.

As the simulation is running the control panel controls the view of the main field (overhead view). It can be toggled, as indicated, to show the simulation field with all agents visible, the MDDs for each team or the aggregate of both of them, the inference models observed thus far, and the aiming and progress of the agents. The data panel for each team is showing the current inference data for each known strategy, highlighting the current most likely strategy in force for the other team(s). The simulation data panel shows the observations and transitions noted so far. When combined with POV cameras for each agent, the simulation output shows the progress of the simulations while provided analysis and insight into the step-wise progress of each agent, each team, and the overall simulation. This panel proved an invaluable tool in understanding the interactions of strategy-based teams and agents as the progress through their assigned tasks. The simulations can also be easily recorded to be walked back through in even greater detail.

The simulation was run effectively and efficiently, the strategies were realized accurately, and the matches run with high-fidelity. The results have been published previously with the standard simulation, but this new simulation produced the same results strategic interactions can be implemented, inferred, and adjusted while the simulation is running.

Conclusion

The goal of this work was to create an interactive-time strategybased simulation that provided constant feedback to the user. This goal was fully realized, with high-fidelity to real- world versions of the game simulated. This work proves that the strategy-based SiMAMT framework can be used in highly- interactive 3D environments that mimic strongly their real- world counterparts. Additionally, the insight provided by the simulations output proved to be an invaluable tool in assessing strategy (both at the individual agent and team level). This success has shown that this highly-complex type of interaction can be modeled, simulated, analyzed, and understood; further, the tool itself can be used to learn more about this type of strategic interaction and to share such data with others.

Future work

This work will next be applied to higher-degree hierarchical structures, like military simulations. This will further prove the applicability of this framework and the usefulness of this simulation environment.

References

1. Luke S, Cioffi-Revilla C, Panait L, Sullivan K, and Balan G, et.al. (2005) “Mason: A multiagent simulation environment,” Simulation, 81: 517-527
2. Horni A, Nagel K, Axhausen KW (2016) The multi-agent transport simulation MATSim. Ubiquity Press London.
3. Franklin DM (2015) “Strategy Inference in Stochastic Games Using Belief Networks Comprised of Probabilistic Graphical Models,”Proceedings of FLAIRS.
4. Franklin DM, Hu X (2017) “SiMAMT: A Framework for Strategy-based Multi-Agent Multi-Team Systems,” International Journal of Monitoring and Surveillance Technology Research.
5. Franklin DM (2016) “Strategy Inference in Multi-Agent Multi-Team Scenar- ios,”Proceedings of the International Conference on Tools for Artificial Intelligence.
6. Anchez PS, Pato D, Martın G (2019)  “Ctransport:  Multi-agent-based simulation”.
7. Firdausiyah N, Taniguchi E, Qureshi A (2019) “Modeling city logistics using adaptive dynamic programming based multi-agent simulation,” Transportation Research Part E: Logistics and Transportation Review, 125: 74-96.
8. Franklin DM (2019) “Hierarchical modeling for strategy-based multi-agent multi-team systems,” in 2019 IEEE Second International Conference on Artificial Intelligence and Knowledge Engineering (AIKE): 259–266.
9. Zhou Y, Wu J, Long C (2018) “Evaluation of peer-to-peer energy sharing mechanisms based on a multiagent simulation framework,” Applied Energy, 222:993-1022.
10. Treuille A, Lewis A, Popovi Z (2006) “Model reduction for real-time fluids,” in ACM SIGGRAPH  2006 Papers, ser.  SIGGRAPH ’USA 826–834
11. “Model reduction for  real-time  fluids (2006) ACM  Trans.  Graph, 25,826-834.
12. Laviers k, Sukthankar G, M. Molineaux DW Darken (2009) “Improving offensive performance through opponent modeling.” in AIIDE.
13. Model reduction for  real-time  fluids (2006) ACM  Trans.  Graph, 25,826-834
14. Michael B, Manuela V (2002) “Multiagent Learning using a Variable Learning Rate,” Artificial Intelligence, 136:212-250.
15. M. Littman M (1994) “Markov games as a framework for multi-agent reinforce- ment learning,” in Proceedings of the Eleventh International Conference on Machine Learning, 157:163.
16. Hu J, Wellman M (1998) “Multiagent reinforcement learning: Theo- retical framework and an algorithm,” in Proceedings of the Fifteenth International Conference on Machine Learning, vol. 242:250.
17. Greenwald A, Hall K, Serrano R (2003) “Correlated Q-learning,” inICML, 20: 242.
18. Simon P, Michael W (2002) “Game Theory and Decision Theory in Multi-Agent Systems,” Autonomous Agents and Multi-Agent Systems, 5:243-254.
19. Stone PVM (1999) “Task decomposition and dynamic role as- signment for real-time strategic teamwork,”Intelligent Agents V: Agents Theories, Architectures, and Languages,293-308.
20. Franklin DM (2016) “Strategy Inference via Real-time Homeomorphic and Isomorphic Tree Matching of Probabilistic Graphical Models,” Proceedings of FLAIRS.
21. Bowling, M (2004) “Existence of multiagent equilibria with limited agents,” J. Artif. Intell. Res. (JAIR) 22:353-384.
22. Vazirani VV (1989) “{NC} algorithms for computing the number of perfect matchings in k3,3-free graphs and related problems,” Information and Computation, vol. 80:152 -164.