Review Article, Res J Econ Vol: 2 Issue: 1
Upper Semicontinuous Representability of Maximal Elements for Non total Preorders on Compact Spaces
Gianni Bosi1*, Paolo Bevilacqua2 and Magali Zuanon3
1Bruno de Finetti Department of Economics, Business, Mathematics and Statistics (DEAMS), University of Trieste, Italy
2Department of Engineering and Architecture, University of Trieste, Italy
3Department of Economy and management, University of Brescia, Italy
*Corresponding Author : Gianni Bosi
Bruno de Finetti Department of Economics, Business, Mathematics and Statistics (DEAMS), University of Trieste, Italy
Tel: +39-040-558-7115
E-mail: gianni.bosi@deams.units.it
Received: October 20, 2017 Accepted: January 02, 2018 Published: January 08, 2018
Citation: Bosi G, Bevilacqua P, Zuanon M (2018) Upper Semicontinuous Representability of Maximal Elements for Non total Preorders on Compact Spaces. Res J Econ 2:1.
Abstract
We discuss the possibility of determining all the maximal elements of a preorder on a compact topological space by maximizing all the functions in a suitable family of upper semicontinuous orderpreserving functions.
Keywords: Preorder; Order-preserving function; Weak utility; Maximal element; Upper semicontinuous function
Introduction
White’s theorem [1] is important since, for every maximal element xo relative to a preorder 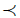 on set X, it guarantees the existence of an order-preserving function u on the preordered set (X,
on set X, it guarantees the existence of an order-preserving function u on the preordered set (X, ) attaining its maximum at xo, provided that an order-preserving function uˈ on (X,
) attaining its maximum at xo, provided that an order-preserving function uˈ on (X,  ) exists. So, at least theoretically, every maximal element is obtained by maximizing a real-valued order-preserving function. When this happens, it is clear that every maximal element is potentially optimal in the sense of Podinovski et al. [2] (i.e., for every maximal element there exists a total preorder extending the original preorder with respect to which such maximal element is best preferred).
) exists. So, at least theoretically, every maximal element is obtained by maximizing a real-valued order-preserving function. When this happens, it is clear that every maximal element is potentially optimal in the sense of Podinovski et al. [2] (i.e., for every maximal element there exists a total preorder extending the original preorder with respect to which such maximal element is best preferred).
In this paper, we generalize White’s theorem to the upper semicontinuous case. This means that we present conditions on a preorder  on a topological space (X,τ) under which, for every maximal element xo relative to
on a topological space (X,τ) under which, for every maximal element xo relative to  , there exists an upper semicontinuous order preserving function u on the preordered topological space (X,τ,
, there exists an upper semicontinuous order preserving function u on the preordered topological space (X,τ,  ) attaining its maximum at xo, provided that an upper semicontinuous order-preserving function uˈ on (X,τ,
) attaining its maximum at xo, provided that an upper semicontinuous order-preserving function uˈ on (X,τ,  ) exists. It should be noted that Bevilacqua et al. [3] already characterized the property according to which every maximal element relative to a preorder on a compact topological space can be obtained by maximizing a transfer weakly upper continuous weak utility for its strict part (see the generalization of Weierstrass Theorem presented by Tian et al. [4]).
) exists. It should be noted that Bevilacqua et al. [3] already characterized the property according to which every maximal element relative to a preorder on a compact topological space can be obtained by maximizing a transfer weakly upper continuous weak utility for its strict part (see the generalization of Weierstrass Theorem presented by Tian et al. [4]).
It is clear that these results are important due to the well-known fact that every upper semicontinuous (more generally transfer weakly upper continuous) function attains its maximum on a compact topological space, and the nearly obvious consideration that a point xo at which an order-preserving function u for a preorder (or, more generally, a weak utility for its strict part) attains its maximum is also a maximal element for  .
.
Notation and preliminaries
Let X be a nonempty set (decision space). A binary relation  on X is interpreted as a weak preference relation, and therefore, for any two elements x, y ϵ X, the scripture
on X is interpreted as a weak preference relation, and therefore, for any two elements x, y ϵ X, the scripture 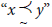 has to be thought of as “the alternative y ϵ X is at least as preferable as x ϵ X “. As usual,
has to be thought of as “the alternative y ϵ X is at least as preferable as x ϵ X “. As usual, 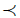 denotes the strict part of a binary relation
denotes the strict part of a binary relation  (i.e., for all x, y ϵ X, x
(i.e., for all x, y ϵ X, x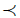 y if and only if
y if and only if 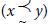 and not
and not 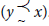 . A preorder is a reflexive and transitive binary relation. An anti-symmetric preorder
. A preorder is a reflexive and transitive binary relation. An anti-symmetric preorder  is referred to as an order. Furthermore, ∼ stands for the indifference relation (i.e., for all x, y ϵ X, x ∼ y if and only if
is referred to as an order. Furthermore, ∼ stands for the indifference relation (i.e., for all x, y ϵ X, x ∼ y if and only if 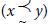 and
and 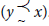 . We have that ∼ is an equivalence relation on X whenever
. We have that ∼ is an equivalence relation on X whenever  is a preorder.
is a preorder.
For every x ϵ X, we set
l(x)={z ϵ X : z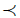 x} i(x)={ z ϵ X : x
x} i(x)={ z ϵ X : x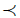 z}
z}
Given a preordered set (X, ), a point xo ϵ X is said to be a maximal element for
), a point xo ϵ X is said to be a maximal element for  if for no z ϵ X it occurs that xo
if for no z ϵ X it occurs that xo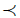 z. In the sequel we shall denote by
z. In the sequel we shall denote by 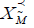 the set of all the maximal elements of a preordered set (X,
the set of all the maximal elements of a preordered set (X, ). Please observe that
). Please observe that 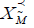 can be empty.
can be empty.
We recall that a function u: (X,  ) → (R, ≤) is said to be
) → (R, ≤) is said to be
i. isotonic or increasing if, for all x, y ϵ X , x  y → u(x) ≤ u(y);
y → u(x) ≤ u(y);
ii. a weak utility for 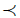 if, for all x, y ϵ X , x
if, for all x, y ϵ X , x  y → u(x) < u(y);
y → u(x) < u(y);
iii. Strictly isotonic or order-preserving if it is both isotonic and a weak utility for 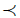 .
.
Strictly isotonic functions on (X,  ) are also called Richter-Peleg representations of
) are also called Richter-Peleg representations of  in the economic literature (see e.g. Richter et al. [5] and Peleg et al. [6])
in the economic literature (see e.g. Richter et al. [5] and Peleg et al. [6])
A preorder  on a topological space (X, τ) is said to be
on a topological space (X, τ) is said to be
i. upper semicontinuous if, for all x, y ϵ X , i(x)={ z ϵ X : x  z} is a closed subset of X for every x ϵ X;
z} is a closed subset of X for every x ϵ X;
ii. Quasi upper semicontinuous if there exists an upper semicontinuous preorder  on (X , τ) such that
on (X , τ) such that 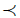 ⊂<.
⊂<.
An upper semicontinuous preorder Ward et al. [7] or more generally a quasi-upper semicontinuous preorder Bosi et al. [8, Theorem 3.1]  on a compact topological space (X , τ) admits a maximal element. As usual, for a real-valued function u on X, we denote by arg max u the set of all the points x ϵ X such that u attains its maximum at x (i.e., arg max u={z ϵ X:(u(z)≤u(x))∀zϵX}
on a compact topological space (X , τ) admits a maximal element. As usual, for a real-valued function u on X, we denote by arg max u the set of all the points x ϵ X such that u attains its maximum at x (i.e., arg max u={z ϵ X:(u(z)≤u(x))∀zϵX}
If τ is a topology on a set X, and  is a preorder on X, then the triplet (X, τ,
is a preorder on X, then the triplet (X, τ,  ) will be referred to as a topological preordered space. The (natural) (interval) topology on the real line R will be denoted by τnat .
) will be referred to as a topological preordered space. The (natural) (interval) topology on the real line R will be denoted by τnat .
Finally, we recall that a real-valued function u on a topological space (X , τ) is said to be upper semicontinuous if u-1(]-∞, α[)={x ϵ X: u(x) < α} is an open set for all αϵR. A very well know result guarantees that every upper semicontinuous real-valued function u on a compact topological space (X , τ) attains its maximum.
Maximal elements of preorders from maximization of upper semicontinuous functions
The following theorem was proved by White et al. [1]. Given any maximal element xo relative to a preorder  on a set X, it guarantees the existence of some order-preserving function u attaining its maximum at xo, provided that an order-preserving function uˈ: (X,
on a set X, it guarantees the existence of some order-preserving function u attaining its maximum at xo, provided that an order-preserving function uˈ: (X,  ) → (R, ≤) exists. Therefore, in order to determine all the maximal elements of a preorder
) → (R, ≤) exists. Therefore, in order to determine all the maximal elements of a preorder  on a set X, the agent maximizes all the functions u in a family U of bounded order-preserving functions for
on a set X, the agent maximizes all the functions u in a family U of bounded order-preserving functions for  . Needless to say, this is a very important opportunity, at least theoretically.
. Needless to say, this is a very important opportunity, at least theoretically.
Theorem: (White et al. [1]): Let (X,  ) be a preordered set and assume that there exists an order-preserving function uˈ: (X,
) be a preordered set and assume that there exists an order-preserving function uˈ: (X,  )→(R, ≤). If
)→(R, ≤). If 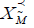 is nonempty, then for every xo ϵ
is nonempty, then for every xo ϵ 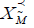 there exists an orderpreserving function u:(X,
there exists an orderpreserving function u:(X,  )→(R, ≤). Such that arg max u=[x0]={zϵ X:z∼xo}.
)→(R, ≤). Such that arg max u=[x0]={zϵ X:z∼xo}.
We now present a generalization of the above theorem to the “upper semicontinuous case”.
Theorem: Let (X, τ,  ) be a topological preordered space, and assume that
) be a topological preordered space, and assume that 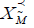 is nonempty. Consider an element xoϵ
is nonempty. Consider an element xoϵ 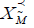 . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
i. There exists an upper semicontinuous order-preserving function uˈ:(X, τ,  )→(R, τnat,≤) and [x0]={z ϵ X:z∼x0} is a closed subset of X;
)→(R, τnat,≤) and [x0]={z ϵ X:z∼x0} is a closed subset of X;
ii. There exists an upper semicontinuous order-preserving function u:(X, τ,  )→(R, τnat, ≤) such that arg max u=[x0]={z ϵ X:z∼x0}.
)→(R, τnat, ≤) such that arg max u=[x0]={z ϵ X:z∼x0}.
Proof: Consider a topological preordered space (X, τ,  ).
).
i) ⇒ (ii) Let uˈ be an upper semicontinuous order-preserving function on (X, τ, X). Without loss of generality, we can assume uˈ to be bounded. Consider a point xo ϵ 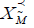 and define the real-valued function u on X as follows for any choice of a positive real δ:
and define the real-valued function u on X as follows for any choice of a positive real δ:
uˈ(x) if not (x∼xo)
u(x)={
sup uˈ(x)+δ if (x∼xo)
White et al. [1, Theorem 1] proved that the above function u is order-preserving for  as soon as uˈ is order-preserving for
as soon as uˈ is order-preserving for  . For the sake of completeness, let us recall here the arguments supporting this consideration. It is clear that uˈ (x) ≤ u (x) for every x ϵ X. In order to show that u is increasing with respect to
. For the sake of completeness, let us recall here the arguments supporting this consideration. It is clear that uˈ (x) ≤ u (x) for every x ϵ X. In order to show that u is increasing with respect to  , consider any two points x, y ϵ X such that x
, consider any two points x, y ϵ X such that x  y. If y∼xo, then it is clear that u(x) ≤ u (x) from the definition of u, On the other hand, if not(y∼xo), then it must be also not(x
y. If y∼xo, then it is clear that u(x) ≤ u (x) from the definition of u, On the other hand, if not(y∼xo), then it must be also not(x  xo), since xo ∼ x
xo), since xo ∼ x  y would imply(xo
y would imply(xo  y ),, and in turn xo∼y due to the fact that xo is a maximal element relative to
y ),, and in turn xo∼y due to the fact that xo is a maximal element relative to  . Hence, since neither x ∼ xo nor y ∼ xo, we have that u(x)=uˈ(x)\≤ uˈ(y)= u(y) from the definition of u and the fact that uˈ is increasing with respect to
. Hence, since neither x ∼ xo nor y ∼ xo, we have that u(x)=uˈ(x)\≤ uˈ(y)= u(y) from the definition of u and the fact that uˈ is increasing with respect to  . In order to show that u is a weak utility for
. In order to show that u is a weak utility for 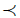 , consider any two points x, y ϵ X such that x
, consider any two points x, y ϵ X such that x 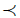 y. Then we have that not(x∼xo), since xo ∼ x
y. Then we have that not(x∼xo), since xo ∼ x 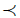 y implies that xo ∼ y (a contradiction, since xo is assumed to be a maximal element for
y implies that xo ∼ y (a contradiction, since xo is assumed to be a maximal element for  ). Therefore, from the definition of u and the fact that uˈ is a weak utility for
). Therefore, from the definition of u and the fact that uˈ is a weak utility for 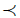 , we have that u(x)=uˈ(x)<uˈ(y)≤u(y), which obviously implies that u(x)<u(y). Further, u attains its maximum at xo and actually, since δ is a positive real, it is clear that (i) arg max u=[xo]={z ϵ X:z∼xo} Therefore, it only remains to show that under our assumptions u is upper semicontinuous. It is clear that u is upper semicontinuous at every point x ϵ X such that x ∼ xo. Therefore, consider any point x ϵ X such that not x ∼ xo and α ϵ R such that u(x)< α. We can limit our considerations to the case when α ≤sup uˈ (x) +δ. Since in this case u(x)=uˈ(x), from upper semi continuity of uˈ there exists an open set Uxˈ containing x such that uˈ(z)< α for every zϵUxˈ. Since [xo] is closed, we have that Ux=Uxˈ-[xo] is an open set containing x such that uˈ(z)=u(z)< α for every zϵ Uxˈ. Hence, u is an upper semicontinuous function.
, we have that u(x)=uˈ(x)<uˈ(y)≤u(y), which obviously implies that u(x)<u(y). Further, u attains its maximum at xo and actually, since δ is a positive real, it is clear that (i) arg max u=[xo]={z ϵ X:z∼xo} Therefore, it only remains to show that under our assumptions u is upper semicontinuous. It is clear that u is upper semicontinuous at every point x ϵ X such that x ∼ xo. Therefore, consider any point x ϵ X such that not x ∼ xo and α ϵ R such that u(x)< α. We can limit our considerations to the case when α ≤sup uˈ (x) +δ. Since in this case u(x)=uˈ(x), from upper semi continuity of uˈ there exists an open set Uxˈ containing x such that uˈ(z)< α for every zϵUxˈ. Since [xo] is closed, we have that Ux=Uxˈ-[xo] is an open set containing x such that uˈ(z)=u(z)< α for every zϵ Uxˈ. Hence, u is an upper semicontinuous function.
(ii) ⇒ (i) Assume that there exists an upper semicontinuous order-preserving function u:(X, τ,  )→(R, τnat,≤) such that arg max u=[xo]={z ϵ X:z∼xo}. If [xo] is not closed, then there exists an element zϵ X-[xo] such that Uz ∩[xo] ≠Φ for every neighborhood Uz of the element z. But this contradicts the fact that u is upper semicontinuous, since in this case u-1(]-∞,u(xo)[), an open set containing z, should contain an element zˈϵ [xo], for which u(zˈ)=u(xo). This consideration completes the proof.
)→(R, τnat,≤) such that arg max u=[xo]={z ϵ X:z∼xo}. If [xo] is not closed, then there exists an element zϵ X-[xo] such that Uz ∩[xo] ≠Φ for every neighborhood Uz of the element z. But this contradicts the fact that u is upper semicontinuous, since in this case u-1(]-∞,u(xo)[), an open set containing z, should contain an element zˈϵ [xo], for which u(zˈ)=u(xo). This consideration completes the proof.
Remark: It is clear that Theorem 3.2 generalizes White’s theorem, due to the fact that these two results precisely coincide when we consider the discrete topology τ on X.
Since in order to determine a maximal element relative to preorder  on a set X it suffices to maximize a weak utility for the strict part
on a set X it suffices to maximize a weak utility for the strict part 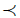 of
of  , the following corollary can be considered as useful. Indeed, the reader can easily verify that the implication “(i) ⇒ (ii)” in Theorem 3.2 is still valid if one considers weak utilities for
, the following corollary can be considered as useful. Indeed, the reader can easily verify that the implication “(i) ⇒ (ii)” in Theorem 3.2 is still valid if one considers weak utilities for 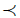 instead of orderpreserving functions uˈ for X
instead of orderpreserving functions uˈ for X
Corollary: Let (X, τ,  ) be a topological preordered space with τ a compact topology. If there exists an upper semicontinuous weak utility uˈ for
) be a topological preordered space with τ a compact topology. If there exists an upper semicontinuous weak utility uˈ for 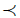 , and [x]={z ϵ X:z∼x} is a closed set for all xϵ
, and [x]={z ϵ X:z∼x} is a closed set for all xϵ 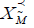 , then for every xo ϵ
, then for every xo ϵ 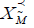 there exists an upper semicontinuous weak utility u for
there exists an upper semicontinuous weak utility u for 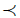 such that arg max [x]={z ϵ X:z∼xo}.
such that arg max [x]={z ϵ X:z∼xo}.
Bosi et al. [8, Theorem 2.11] proved that there exists an upper semicontinuous weak utility for the strict part 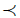 of a quasi-upper semicontinuous preorder
of a quasi-upper semicontinuous preorder  on a second countable (i.e., with a countable base) topological space(X, τ). Hence, we get the following corollary.
on a second countable (i.e., with a countable base) topological space(X, τ). Hence, we get the following corollary.
Corollary: Let (X, τ,  ) be a topological preordered space. Assume that τ is a compact and second countable topology, and that
) be a topological preordered space. Assume that τ is a compact and second countable topology, and that  is quasi upper semicontinuous. If [x]={z ϵ X:z∼x} is a closed set for all xϵ
is quasi upper semicontinuous. If [x]={z ϵ X:z∼x} is a closed set for all xϵ 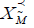 , then for every xo ϵ
, then for every xo ϵ 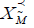 there exists an upper semicontinuous weak utility u for
there exists an upper semicontinuous weak utility u for 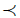 such that arg max [x]={z ϵ X:z∼xo}.
such that arg max [x]={z ϵ X:z∼xo}.
Conclusion
In this paper, following the spirit of a theorem of White et al. [1], we have presented some results concerning the representation of the set of all maximal elements of a preorder on a compact topological space by means of the maximization of all functions in a suitable family of bounded upper semicontinuous order-preserving functions. The more delicate problem of characterizing the possibility of representing all the maximal elements for a preorder on a compact topological space by means of the maximization of finitely many upper semicontinuous order-preserving functions will be hopefully considered in a future paper.
References
- White DJ (1980) Notes in decision theory: optimality and efficiency II. Eur J Oper Res 4: 426-427.
- Podinovski VV (2013) Non-dominance and potential optimality for partial preference relations. Eur J Oper Res 229: 482-486.
- Bevilacqua P, Bosi G, Zuanon M (2018) Maximal elements of preorders from maximization of transfer upper continuous weak utilities on a compact space. Far East J Math Sci 103: 213-221.
- Tian G, Zhou J (1995) Transfer continuities, generalizations of the Weierstrass and maximum theorems: a full characterization. J Math Econ 24: 281-303.
- Richter MK (1966) Revealed preference theory. Econometrica 34: 635-645.
- Peleg B (1970) Utility functions for partially ordered topological spaces. Econometrica 38: 93-96.
- Ward LE (1954) Partially ordered topologicl spaces. P Am Math Soc 5: 144-161.
- Bosi G, Zuanon ME (2017) Maximal elements of quasi upper semi continuous preorders on compact spaces. Econ Theory Bulletin 5: 109-117.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi