Research Article, J Hydrogeol Hydrol Eng Vol: 8 Issue: 1
A Laboratory Scale Drawdown Testing for the Determination of a Model Sand Pack Aquifer Hydraulic Parameters
1Department of Process Engineering and Applied Science, Dalhousie University, Halifax, Nova Scotia, Canada
2Department of Chemical Engineering, School of Science and Technology, Cape Breton University, NS B1P 6L2, Canada
*Corresponding Author : Amadu M
Part time Assistant Professor, Process Engineering and Applied Science, Dalhousie University, Nova Scotia, Canada
E-mail: mm846771@dal.ca
Received: June 19, 2019 Accepted: July 05, 2019 Published: July 12, 2019
Citation: Amadu M, Miadonye A (2019) A Laboratory Scale Drawdown Testing for the Determination of a Model Sand Pack Aquifer Hydraulic Parameters. J Hydrogeol Hydrol Eng 8:1.
Abstract
Naturally occurring hydrocarbon fluids and ground water are two major geological resources essential for both energy and domestic driven civilizations at all levels of human activities. These two resources are hosted by subsurface geologic media commonly called reservoirs or aquifers. The development and supply of these resources in a systematic and guaranteed manner requires knowledge of their subsurface environments of flow. In both ground water and petroleum engineering communities, the same diffusion type equation describes subsurface fluid flow and most importantly, the analytical solutions of these equations have been greatly exploited for both formation and resource evaluation purposes. This study uses a newly installed ground water flow unit at the Chemical Engineering Laboratory of Dalhousie University (Halifax- Nova Scotia Canada) to obtain the first ever laboratory-scaledrawdown testing data for the determination of the hydraulic conductivity of a model sand pack aquifer.Conventional plots of experimental data in this study have been found to be perfectly similar to those obtained using actual field data from field-scale drawdown testing. Accordingly, absolute permeabilities, hydraulic conductivities, skin factors and other theoretically deduced parameters based on rigorous mathematical analysis of drawdown test data have been found to be physically realistic.
Keywords: Diffusion equation; Permeability; Pressure transient; Total compressibility; Skin factor
Introduction
It is noteworthy that the efforts of groundwater and petroleum engineers have led to the presentation of what is popularly known in the literature as the radial diffusion equation [1,2]. In principle, scientists have put together the principle of mass balance, the fundamental equation for flow in porous media presented by Darcy [3] and an equation of state linking fluid density to pressure to arrive at an equation that links subsurface fluid flow pressure to distance and time. This is the radial diffusion equation. The analytical solution to this equation has provided a fundamental tool for determining hydraulic conductivity and other related parameters in groundwater well testing [4]. In petroleum engineering practice, the solution based on the logarithm approximation to the solution of the radial diffusion equation has been used for permeability and skin factor determination in well testing [5].
In both groundwater and petroleum engineering practices, hydraulic parameters such as hydraulic conductivity, permeability and skin factor have been deduced from solutions of the radial diffusion equation using field tests data in well testing [6] Consequently, any system that permits measurement of time and pressure in a manner that can be described by any of the known theoretical foundations governing permeability measurements in the literature can be effectively exploited for the determination absolute permeability. What is more, in the hydrogeological literature, excellent laboratory scale studies involving simulation and or determination of aquifer constants have been reported, in addition to a recent laboratory scale investigation of skin [7] but none has been reported involving drawdown testing.
One major problem encountered by geotechnical engineers is dewatering during excavation [8-10]. The Groundwater unit H 167 was originally built with the intent to study the 3 dimensional groundwater flow in addition to studies of dewatering problems in geotechnical engineering. Owing to its excellent features, which permit it to be adopted for transient pressure measurements integrating a sand pack as a model aquifer and a perforated tube as a model well, laboratory-scale drawdown or pumping test experiments will be conducted in the present study. In this regard, it is intended to create a model reservoir or aquifer using the newly built groundwater flow unit installed at Dalhousie University Department of Process Engineering and Applied Science laboratory, and to conduct hydraulic experiments aimed at collecting data for determining the absolute permeability of a sand pack. The basis of the test will be the hydrogeological drawdown testing on a laboratory scale.
Literature Review
The role of laboratory scale model in hydrogeological studies
In the hydrogeological literature, some numerical software have been used to calculate groundwater flow in fractured rocks under different assumptions, employing the MODFLOW-CFP for hybrid modelling [11]. On the other hand, laboratory analog models were widely used before the advent and proliferation of computer supported numerical modelling and these models are nowadays being considered very important, helping to understand hydrological processes and verify numerical models. For example, laboratory models were made by Faulkner [12] and Wu and Hunkeler in 2013. In Hungary, well-known laboratory model researches were made by Öllõs [13,14]. Two numerical groundwater models based on a laboratory scale karst analog model by [11] were created using CFP and MODFLOW-2005 to determine if CFP simulates flow in karst conditions more accurately. The analog model was rectangular and constructed out of Plexiglas, with a 2 cm diameter conduit located at the bottom of the model, and a matrix domain composed of glass sand sized beads overlying the conduit. Overall, the analog model was 60 cm long, 26 cm wide and 2 cm thick. The interior of the matrix domain, including the inflow and outflow reservoirs was 57.8 cm long, 24.1 cm wide, and 2 cm thick. The conduit portion of the analog model was 57.8 cm long, 2 cm wide and 2 cm thick. However, in spite of their importance, there are only few available studies about laboratory analog models of groundwater flow in fractured rocks, not to speak of their applications to laboratory scale drawdown testing. this knowledge gap will be filled. In the following sections, the Petrophysical and hydrogeological bases of the present study and their interrelationships will be reviewed briefly, but concisely as part of the literature resources for achieving the ultimate objective.
Permeability models and their bases
Permeability is the ability of sediments to transmit fluids under pressure gradients. Two types can be distinguished. One is the absolute permeability, defined as the ability of a porous system to transmit fluid under conditions where there is100 percent saturation of the flowing fluid. The other is the effective permeability, defined for the case where multiphase flow of different fluids occurs in a porous medium. Two types of permeability models can be distinguished. They are Petrophysical and hydraulic models. Petrophysical models link permeability to Petrophysical parameters such as porosity, grains, pore sized distribution index and pore throat diameter [15] The hydraulic model, famous among which is the Darcy equation links permeability to pressure gradient, flow rate, the dynamic viscosity of the flowing and the cross sectional area of flow. In the following sections, the Petrophysical and hydraulic models of permeability will be reviewed.
Derivation of a petrophysical model of absolute permeability from a hydraulic model
Hydraulic model: For a porous system, the rate of fluid flow under a given pressure gradient is directly proportional to the product of the cross sectional area orthogonal to flow and the imposed pressure gradient and inversely proportional the dynamic viscosity of the flowing fluid. The constant of proportionality is empirically called permeability and this is the basis of the Darcian law written as [16]:
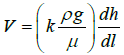 (1)
(1)
Where:
v =specific discharge
ρ =density of fluid-kg/m3
g =dynamic viscosity of flowing fluid-Pa.s
g =gravitational constant m/s2
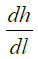 = hydraulic gradient-Pa/m
= hydraulic gradient-Pa/m
k =absolute permeability-m2
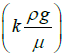 =hydraulic conductivity-m/s
=hydraulic conductivity-m/s
Petrophysical permeability models: In the geologic literature, attempts to link sediment permeability to material parameters abound, and excellent summaries exist [17,18]. In this regard, a widely used permeability model was proposed by Kozey in 1927 [19] and another by Carmen in 1956 [20]. To account for the permeability of a mixture system, Yin in 1993 derived an equation based on the Kozeny-Carmen equation [21].
The derivation of Kozey’s famous equation is based on a bundle of parallel capillary tube model having a definite cross-sectional area of flow. Accordingly, the flow through each tube was modelled like the Hagen Poisseuille flow through a capillary tube, derived from the solution of the Navier Stokes equation. Consequently, by equating the volumetric flow rate to Darcy’s equation, Kozeny arrived at the following equation for absolute permeability [16]:
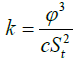 (2)
(2)
Where:
St =sediment porosity-fraction
St =specific surface area per unit volume of sedimemt-m-1
C=c is a dimensionless constant that depends on grain shape and orientation of tubes
Kozeny’s equation is such that the specific surface area per unit volume contains indirect information about both pore size and pore volume. To separate the two Petrophysical parameters, the specific surface area per unit volume was linked to the specific surface area of sediment per unit mass as [20]
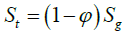 (3)
(3)
Following this modification, Kozeny’s equation can be written as the Kozeny Carmen equation as:
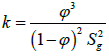 (4)
(4)
Where:
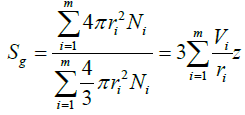 (5)
(5)
Vi =volume fraction of the ith component
ri =radius of the ith component
Ni =number of spheres of component i
Derivation of permeability model for a mixture system
To derive a permeability model of a sandy-clay mixture system, Eqn. (3) was substituted into the Kozeny-Carmen equation and this led to the following equation [21]
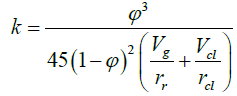 (6)
(6)
Where:
Vg=grain volume
rg=radium of grain
Vcl=volume of clay
rcl=radius of clay mineral
Flow model in porous media
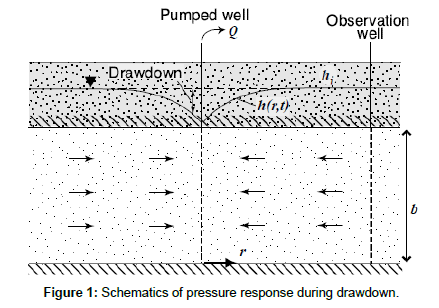
Field Scale Based Model in Hydrogeology: The equation governing the transient or unsteady state ground water flow in an aquifer (Figure 1) is given as [1]
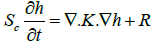 (7)
(7)
In this equation, 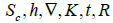 are storage coefficient, hydraulic head, differential operator, hydraulic conductivity, time, and source term respectively [22].
are storage coefficient, hydraulic head, differential operator, hydraulic conductivity, time, and source term respectively [22].
The source term could result from induced filtration from streams, steady and unsteady state leakage from confining beds as well as recharge from precipitation and evapotranspiration.
For radial flow geometry, Eqn. (1) can be written in terms of partial derivatives as [23]
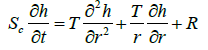 (8)
(8)
Where:
SC=storage coefficient- [Pa-1]
T=transmissivity- [m2 s-1]
h=hydraulic head [m]
r=radial distance from well [m]
t=source term-[s]
R=[ms-1]
Equation (1) has been derived on the basis of mass balance, equation of state approach and the fundamental Darcy equation for flow in porous media. The analytical solution of this equation based on the appropriate boundary conditions gives hydraulic head as a function of time and space in the flow field. The following section will be devoted to aspects of the analytical solution.
Solution in hydrogeology: Several analytical solutions exist for the radial diffusion equation in one dimension [24-26]. The most widely used analytical solution for pressure transient testing in groundwater engineering is that due to Thesis [27]
This is given as:
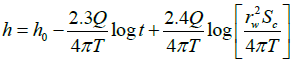 (9)
(9)
In this equation, ho and h are initial head before drawdown testing and transient head respectively.
In Eqn. (9), the gradient of the plot is given as:
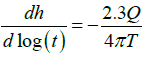 (10)
(10)
Where:
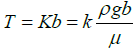 =Transmissivity of aquifer
=Transmissivity of aquifer
μ =Dynamic viscosity of the fluid
ρ =density of flowing fluid-[kgm3]
g=gravitational acceleration-[ms2]
b=aquifer thickness-[m]
Q=flow rate-[m3s-1]
K=hydraulic conductivity [ms-1]
k=absolute permeability of sediment-[m2]
Substituting gives:
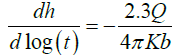 (11)
(11)
Hence,
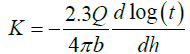 (12)
(12)
Equation (12) will be referred to in the appropriate section regarding how it can be put to use to achieve the principal objective of this paper.
The skin and wellbore storage effects
For a single well pumping from a confined aquifer, the two most important factors that cause a deviation from the theoretical straight line described by Eqn.(9) are skin and wellbore storage effects [28], which cause additional drawdown in the wellbore that is not representative of the drawdown in the aquifer. For a well fully penetrating an aquifer, where non-linear losses are negligible, integration of skin into the solution to the radial diffusion equation leads to the following equation [29]:
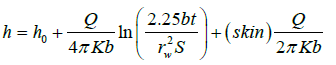 (13)
(13)
Hence:
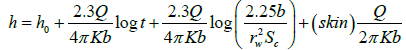 (14)
(14)
Where:
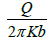 =skin effect-m
=skin effect-m
skin =skin factor-dimensionless
Equation (8) can be written as
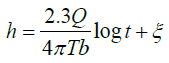 (15)
(15)
Equation (14) can be written as
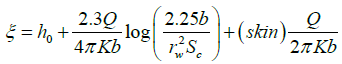 (16)
(16)
Therefore, a plot of drawdown versus the natural logarithm of time gives a straight line with a vertical intercept from which the skin factor can be deduced to access the extent of damage or stimulation of a well in the drilling operation. Such an intercept is defined by ξ, from which the skin can be computed as:
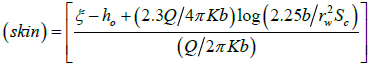 (17)
(17)
The storage coefficient is a measure of a system’s (water plus sand) compressibility and it is given as [30]
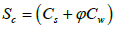 (18)
(18)
Where,
Cw =storage coefficient-[m-1]
Cw =compressibility of water-[Pa-1]
Õ =porosity of sand pack
Cs =compressibility of sand -[Pa-1]
Sand pack compressibility in the absence of centrifugal induced gravity is calculated as [31]
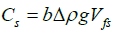 (19)
(19)
Where:
Δρ =density difference between sand and water- [kgm-3]
Vfs =volume fraction of sand
g=gravitational acceleration [ms-2]
Insertion of Eqn. (11) and Eqn. (12) into Eqn. (10) gives skin as:
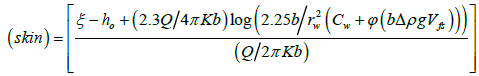 (20)
(20)
Equation (20) will be used for computation of skin in this paper.
Generally, the effect of wellbore storage is to delay fluid flow from the aquifer to the wellbore during drawdown testing [32]. In the literature, a rigorous mathematical analysis of early transient test data taking into account fluid expansion in the wellbore leads to the following equation [33]:
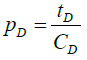 (21)
(21)
Where:
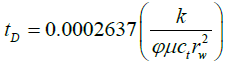 (22)
(22)
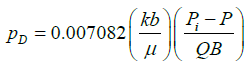 (23)
(23)
The dimensionless wellbore storage coefficient is linked to the wellbore storage constant (C) as
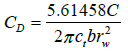 (24a)
(24a)
Thus, the well bore storage constant can be calculated as:
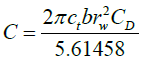 (24b)
(24b)
In this equation, C is the wellbore storage constant in m3Pa-1
Therefore, a plot of dimensionless pressure versus dimensionless time will give a straight line through the origin, where the gradient is given by the reciprocal of the dimensionless wellbore storage coefficient.
Determination of aquifer absolute permeability using hydraulic flow model
In this study, our objective is to determine the absolute permeability of a model sand pack aquifer using the flow model, which is also the hydraulic model. In this regard, Eqn. (9) shows that a plot of the logarithm of head versus time will give a straight line with a negative gradient, such that, the following can be written. Therefore, Eqn. (9) provides an opportunity for experimentally determining the absolute permeability of a model Aquifer. Consequently, the gradient of the plot which is Eqn. (10) can be algebraically manipulated to solve for absolute permeability. In this regard, apart from the gradient which is calculated from the plot, all other parameters (fluid density, fluid dynamic viscosity, tube or well radius and gravitational acceleration constant) are known or can be measured under experimental conditions. Absolute permeability determination from experimental data is, therefore, a possibility.
Experimental capabilities of the groundwater flow unit and our experimental objective
Experimental capabilities of the groundwater flow unit: A perfect understanding of the hydrological principles governing ground water flow is useful for the design of reliable structures involving excavation, pits and drainage systems. The groundwater flow unit HM 167 (Figure 2) permits a three-dimensional investigation of groundwater flow. It has a trainer, which consists of a tank into which sand can be loaded for filling. Consequently, various hydraulic or Petrophysical models can be created based on sand grain sizes. Water can be admitted into the tank via two open-seam tubes that can be separately activated via valves. This advantage results in different experimental possibilities using this system. In this regard, the investigation of different methods of groundwater extraction is made possible and easy by using two wells with open-seam. These tubes are also individually activated by valves.
Our experimental objective: In view of the above mentioned hydraulic sophistication of the groundwater flow system, our principal objective in this study is to use the valve and well system to induce flow in a porous sand pack system. Accordingly, we intend to determine the absolute permeability of a sand pack system using the hydraulic model of absolute permeability derived through the analytical solution of the radial diffusion equation (3). Therefore, the generation of pressure transient pulses through the application of impulses or flow rates [34] will be Key to achieving our objective using the well-valve system.
Experimental program: The experimental program involved acquiring well flowing head/pressure versus time in drawdown testing. and the testing of data against Eqn. (9), and to also facilitate hydraulic conductivity and skin factor computations using Eqn. (12) and Eqn. (9) respectively.
Materials and Methods
Equipment
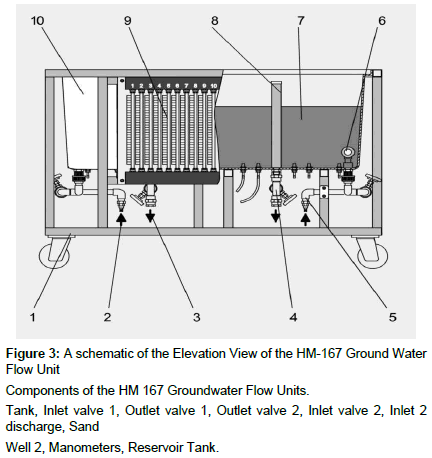
The system for the model reservoir is a newly installed ground water flow unit in Dalhousie University Chemical Engineering laboratory (Figure 3). This unit was manufacture by G.U.N.T. Gerätebau GmbH in Germany. It is capable of simulating ground water flow by indicating flow pressure variation with time at various points of the unit using corresponding manometers. The following are the dimensions:
Length: (1.10 m) 3 feet 3 inches
Breadth: (0.65 m) 2 feet
Depth: (0.70 m) 2 feet 2 inches
Components of the HM 167 Groundwater Flow Units
Tank, Inlet valve 1, Outlet valve 1, Outlet valve 2, Inlet valve 2, Inlet 2 discharge, Sand
Well 2, Manometers, Reservoir Tank
Materials
The following materials and equipment were available
Sandy material
Stop Watch (Fisher Scientific Clip-On Stopwatch)
Beakers
Experimental procedure
Creating a model aquifer in the laboratory: Using the HM 167 Ground Water Flow unit, a model aquifer was made with coarse sand grains [35] using using Ottawa sand and tap water as the flowing fluid. Sand fractions were sieved using sieve numbers 40 to 60 (Figure 4) and this provided a sand pack with grain diameter ranging from 2 mm to 4 mm.
The following were the procedures involved in creating the model system:
1. About 100 kg of sand was sieved from the bulk pile using the sieve equipment assembly in order to get the required range between 2 mm and 4 mm diameter of sand grains.
2. The HM 167 tank was filled with the sieved sand to a level of 200 mm.
3. The inlets valves were connected to the laboratory water source and the outlet valve were connected to the laboratory discharge container (beaker).
4. Several test experiments were run based on the instructions from the manual of the HM 167 as required if equipment is ready.
5. A well (2) was created using a perforated metal tube such that flow was through the entire length in the sand pack
Determining model aquifer porosity: Saturation method, in which the pore volume of a porous sample may be determined from the difference between saturated and dry masses was used in this study [36]. In determining the porosity of the model reservoir, a sample of the sand was weighed in a cylindrical tube of known volume 1800 ml when dry and again when water was added to fill the entire void of the sand. The difference between the mass of the sand plus beaker and water and sand plus beaker gives the mass of the water which fills the void space. The approach for porosity determination is reported in Appendix A2.
Drawdown testing procedure
Achieving bottom-hole pressure conditions similar to actual field conditions of flow: Under typical pressure transient testing in petroleum reservoir engineering and drawdown testing in ground water engineering, transient pressure and head responses of the reservoir are measured using bottom-hole pressure gages installed at the bottom of the well [37]. Since bottom hole pressure gage was not available, the strategy adopted was to select from among the various manometers the one that is closest to the well. Accordingly, the transient pressure/head readings of the manometer number 4 were those regarded as representative of the pressure or head responses of the flow system. The following were the experimental procedures:
1. The first draw down test was run using well 1. Well 2 was shut down during the whole experiments.
2. The water level in the tank was filled up to different levels in each experiment
3. The well was produced through outlet valve 1 and the bottomhole pressure and flow rate were determined versus time.
4. The bottom-hole head variation corresponding to transient pressure response was recorded against time.
5. In all, 3 drawdown experiments were performed at ambient conditions (standard laboratory conditions)
6. Accordingly, pressure versus time data enabled pressure data to be calculated to transient head data.
Results and Discussion
Semi-log plots
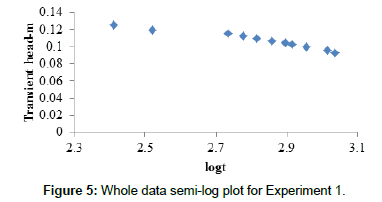
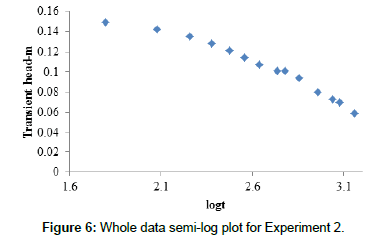
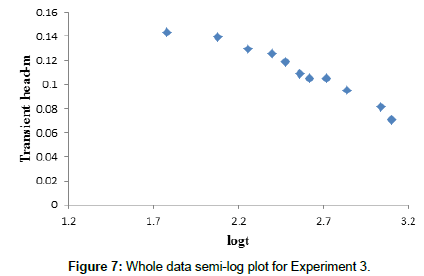
The properties of a confined aquifer can be found by developing the time drawdown relationship based on Eqn. (9). If the pumping time is sufficiently long, a plot of the transient h(r,t) observed in a particular piezometer at distance r from the pumped well versus the logarithm of time t, will appear as a straight line. Therefore, a whole experimental data plot will only reveal the theoretical straight line after transient pressure or head pulse has propagated long enough from the wellbore into the aquifer (Figures 5-10). Accordingly, Figure 5 through Figure 7 show whole experimental data plots taken from Appendices C1, C2 and C3, with the semi-log straight lines appearing sometime after the start of the tests.
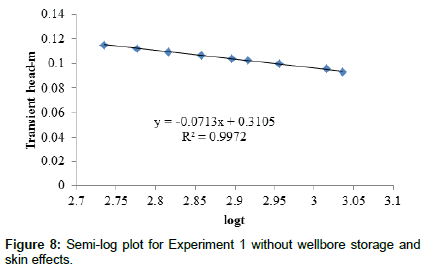
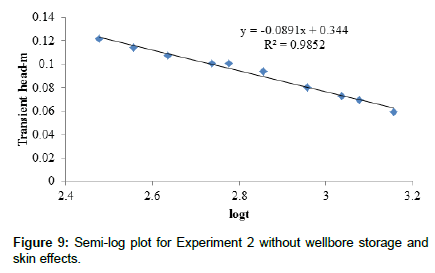
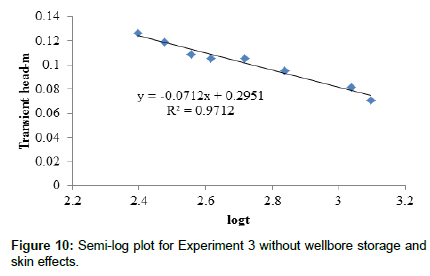
Figure 8 through Figure 10 show portions of the data for experiments 1, 2 and 3 respectively, where test data based on Appendices B1, B2 and B3, were acquired after long enough times to develop the theoretical semi-log plots. Accordingly, the gradients of the plots for experiments 1, 2 and 3 are -0.0713, -0.0891 and -0.0712 respectively, with regression coefficients 0.99, 0.98 and 0.97 respectively. The mean for gradients is -0.0772 while that for regression coefficients is 0.98. In this regard, the mean regression coefficient of 0.98 is sufficient enough to fit experimental data into theoretical development.
Table 1 shows aquifer parameters computed using the gradients of the plots. Accordingly, Column 2 shows computed absolute permeabilities using the definition for tranamissivity while Column 3 shows the milliDarcy equivalence. Column 4 shows hydraulic conductivity values computed using the gradient of the plot in Eqn. (12), while Column 5 shows computed dimensionless skin factors using Eqn. (20). Equation (18) was used for calculating the storage Coefficient (Sc) of aquifers. Column 6 shows computed apparent wellbore radius using the relationship between apparent wellbore radius, true wellbore radius and the dimensionless skin factor parameter (Matthews and Russel, 1967). The last column, Column 7, shows computed grain radii using computed absolute permeability values and the experimentally determined porosity of the sand pack. In this regard, the petrophysical absolute permeability model (Eqn.6)) that integrates sediment porosity, grain radius of sediment component and the volume fraction of sediment component was used, assuming the volume fraction of clay is zero (i.e. 100% sand grain).
| Experiment no. | Permeability (m2*10-10) | Permeability Md |
Hydraulic conductivity (ms-1*10-3) |
Skin | Apparent radius (m) |
Grain radius (mm) |
|---|---|---|---|---|---|---|
| 1 | 4.19 | 530.8 | 4.13 | -1.7 | 0.26 | 3.25 |
| 2 | 5.31 | 538.33 | 4.24 | -2.08 | 0.38 | 3.67 |
| 3 | 4.34 | 549.65 | 3.9 | -1.69 | 0.26 | 3.31 |
| Average | 4.61 | 539.6 | 4.1 | -1.83 | 0.34 | 3.41 |
Table 1: Computed aquifer and well parameters from graphical plots.
Computed grain radii as indicated in Column 7 of Table 2 are 3.25 mm, 3.67 mm and 3.31 mm for Experiments 1, 2 and 3 respectively, with a mean value of 3.41 mm. Based on the standard approach for grain size classification [38], the computed valaues and their mean fall within coarse grain size fractions.
| Experiment no. | Dimensionless wellbore Storage coefficient | Wellbore storage constant bbl psi-1*10-9 | Regression coefficient |
|---|---|---|---|
| 2 | 21.28 | 4.51 | 0.93 |
| 3 | 23.81 | 5.1 | 0.96 |
| Average | 22.55 | 4.31 | 0.96 |
Table 2: Dimensionless wellbore storage coefficients and computed wellbore storage constant.
Domenico and Schwartz [39] studied the permeabilities of different sediments cosnsiting of different grain sizes and or ranges of grain sizes for unconsolidated sediments. Appendix D, shows their results. The sand pack aquifer in the present study was constructed using sand grains with grain sizes within coarse grain sizes. The hydraulic conductivity values computed in the present study range from 3.90 *10-3 ms-1 to 4.2 *10-3 ms-1 with a mean value of 4.10*10-3 ms-1. Appendix D, shows that the hydraulic conductivity for unconsolidated coarse grain sand sediment ranges from 9*10-7 ms-1 - 6*10-3 ms-1. Therefore, the mean value of hydraulic conductivity obtained in the present study based on sand pack aquifers with the same coarse grain sand fraction falls within that reported by Domenico and Schwartz implying values of experimentally determined absolute permeabilities and their average value represent true hydraulic parameters various sand pack aquifers. What is more, Mavis and Wisely [40] studied the permeability of Ottawa Sands and plotted hydraulic conductivity versus porosity. Appendix C shows their work. The porosity of the sand pack in the present study is 0.40. Then graph of [40] shows that the hydraulic conductivity of Ottawa Sands pack with porosity 0.40 coincides with a line whose vertical permeability value is 1100 ft per day, which is equivalent to 4.13 *10-3 ms-1 and very close to the mean of 4.10*10-3 ms-1 in Table 1.
The dimensionless skin factor parameter serves to describe the damage or improvement to the region surrounding the wellbore that is caused by drilling and completion practices [41-43]. Generally, a negative skin refers to well stimulation while a positive value refers to damage or permeability impairment. What is more, a positive skin is referred to a zone near the well having lower permeability than the original formation due to well construction. On the other hand, A negative skin is a zone which has higher than other part of aquifer formation [44]. In the present study, values of the parameter are negative, implying well stimulation that stems from the mechanical agitation of the sand pack in the vicinity of the perforated tube used as a model well in the sand pack aquifers. Accordingly, apparent wellbore radius must be bigger than actual tube or well radius, and this is seen in Table 1.
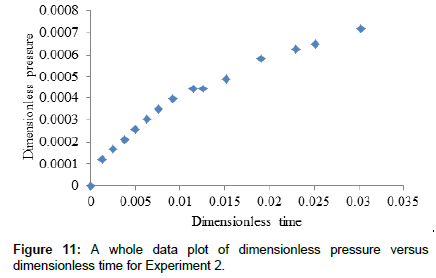
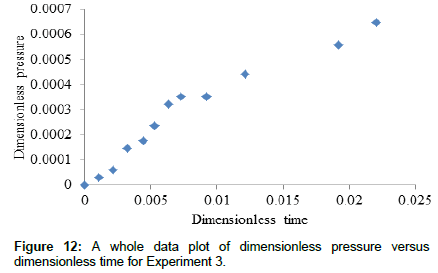
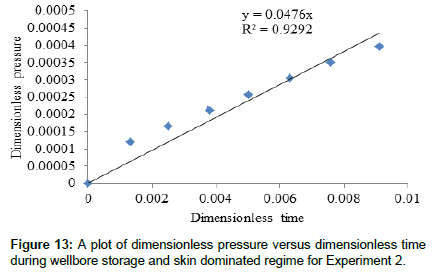
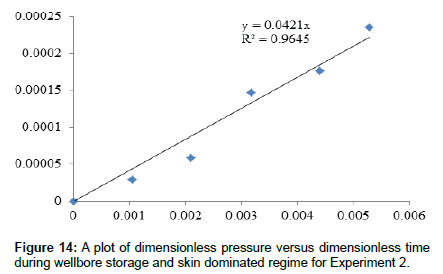
Dimensionless data plots
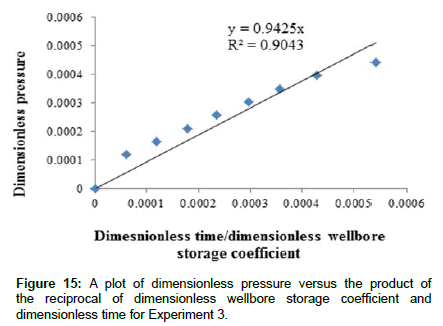
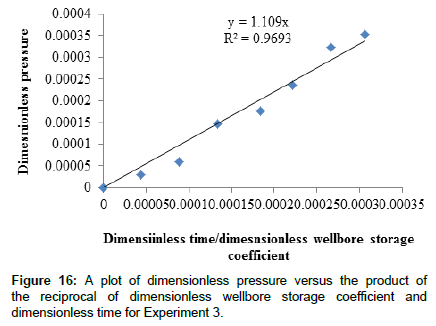
Figures 11 and 12 show plots of dimensionless pressure versus dimensionless time for all experimental data while Figures 13 and 14 show similar plots for wellbore storage and skin effects dominated regime. Data for plots were taken from Appendix B4 and Appendix B5. Theoretically, a plot of dimensionless pressure versus dimensionless time during wellbore storage and skin effect should give a straight line passing through the origin with a gradient equal to the reciprocal of the dimensionless wellbore storage coefficient, Accordingly, Figure 11 and Figure 12 show two obvious trends where early data plots tend to fall on straight line, with that of Figure 12 tending to clearly obey theory. Therefore, Figure 13 and Figure 14 show straight line plots with gradients 0.0476 and 0.0421 and regression coefficients 0.93 and 0.96 respectively, the coefficients being sufficient enough to account for the theoretical basis [33] of the plots.
Table 2 shows computed wellbore dimensionless storage coefficient and wellbore storage coefficients for all tests using the gradients from Figure 13 and Figure 14. The values are 21.28 and 23.81 for Experiment 2 and Experiment 3 respectively with a mean value of 22.55, all to 2 decimal places. Accordingly, computed wellbore storage constants using Eqn. (24b) are 4.51 *10-9 and 5.10*10-9 bbl Pa-1 for experiment 2 and Experiment 3 respectively with a mean value of 4.32*10-9 bbl Pa-1. Data for Experiment 1 were not considered for dimensionless plots because from Figure 2, only two data points are found related to the wellbore storage and skin dominated regime, and this gives reason for discounting this experiment. Generally, wellbore storage which also depends on well fluid compressibility acts to delay flow of fluid from aquifer formation [32]. In this regard, examination of the logarithm of time for the beginning of the theoretical semi-log plot straight lines for Experiment 2 and Experiment 3, shows that the former straight line begins at log(t) equal to 2.48 while that for the latter begins at log(t) equal to 2.4. The constant pumping rates for the two tests are 3.51*10-4 m3s-1 and 2.81* 10-4 m3s-1 respectively, with a mean of 3.16 * 10-4 m3s-1 which is very close to any of the flow rates. Therefore, values of dimensionless parameters regarding the wellbore storage mechanism for both tests represent the non-linear behavior of transient pressure/head pulse propagation for the same sediment during early time.
Theoretically, Eqn. (21) shows that a plot of dimensionless pressure versus the reciprocal of dimensionless wellbore storage coefficient multiplied by dimensionless time, should give a straight line passing through the origin with a unit slope. Accordingly, Appendix B6 shows processed data and Figures 15 and 16 show plots for Experiment 2 and Experiment 3 respectively. The gradients are 0.94 and 1.10 to 2 decimal places for experiment 2 and Experiment 3 respectively. The average gradient is 1.10.These values are closer to unity, which testifies to the validity of experimental data regarding the theoretical model. Also, the regression coefficients for the plots are 0.90 and 0.97 to 2 decimal places with a mean of 0.94 and these are further testimonies of the validity of experimental data pertaining to the wellbore storage and skin effect dominated regime [28].
Compared to typical values of wellbores storage constant encountered in connection with petroleum well tests, which are 0.001 to 0.01 [45], values deduced in this study are very low as seen in Table 2. The reason is that petroleum accumulations are encountered at elevated temperatures which increase well fluid compressibility. The exceptionally very low values obtained in the present study can be explained based on the concept of the parameter. Theoretically, it is the change in fluid volume per unit pressure drop when the well is suddenly put on production. Generally, the bigger the extent to which the bottom hole fluid is compressed by overlying fluid column in the well bore, the bigger will be the decompression of bottom hole fluid following production, and the greater will be the delay in the production of formation fluid. Under this condition, well bore storage constant will be bigger. In the present study, the column of fluid or water is very small compared to that in a petroleum well or actual aquifer environment. Therefore, the original compression of water at the bottom of the model well was very small, meaning decompression of compressed water was very negligible leading to very small values of well bore storage constant.
Aquifer transmissivity and yield
The transmissivity was estimated using the simplified form of the Thesis solution developed by [46] called the Cooper-Jacob method. The approach is based on the assumption that after a significantly long pumping time when pressure pulse has propagated far from the well bore, test data obeys a straight line semi-log plot. Under this condition, the slope of the line can be used for transmissivity computation as:
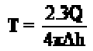
In this equation Δh is the draw down occurring over one log cycle.
Table 3 shows computed transmissivities and yields, Values of transmissivities are very close to each other with a mean of 0.00064, which is also very close to calculated values. The yields are also very close to each other except that for Experiment 1. In all, computedtransmissivities and yields indicate that they all belong to the same sand pack aquifer.
| Experiment no. | 1 | 2 | 3 | Average |
|---|---|---|---|---|
| Transmissivity (m2s-1) | 0.0005 | 0.0007 | 0.00072 | 0.00064 |
| Yield-m3d-1 | 23.56 | 30.21 | 31.02 | 28.26 |
Table 3: Computed aquifer transmissivity and yield.
Engineering importance of our work
That newly installed groundwater flow model was built with the intent to study 3 dimensional groundwater flow regimes and to also study dewatering problems during excavations. Consequently, the importance of the present study stems from the fact it draws the attention of both researchers in academia and the manufacturer to the possibility of its adoption for drawdown testing at laboratory scale, making it possible to estimate hydraulic conductivity of sandpacks and or sand filters. Accordingly the results of this study will also permit the use of the groundwater flow unit for the determination of sediment samples for the design of filtration systems [47-49]. In applied hydrogeology, values of hydraulic conductivities and yields obtained in this study serve as a guide to expected ones in connection with aquifers of alluvial valleys and alluvium in tectonic valleys [50].
Conclusion
The model aquifer was considered to be initially saturated with tap water of ambient dynamic viscosity and density (room temperature experimental conditions). It is further assumed that aquifer drawdown is everywhere small in comparison to the initial saturated thickness,b , such that b can be considered as constant. Ground water withdrawn is assumed to derive from aquifer storage of a constant Sc, calculated using an equation that exists elsewhere [51] and drainage from the water table decline. This study has managed to provide the first laboratory experimental data that fit into the analytical solutions of the radial diffusion equation which describes hydrocarbon and ground water flow in porous media. The following sums up the conclusion of this study:
1. Using transient pressure data associated with draw down testing of a model aquifer in this study, a model aquifer hydraulic characteristics associated with those commonly determined for field-scale drawdown testing in hydrogeology practice have been determined,
2. The hydraulic conductivity values and mean determined in this study for Ottawa sand agree with that of a reported value for Ottawa sand pack of the same porosity found in the literature,
3. The mean value of hydraulic conductivity determined in this study agree with that reported in the literature based on the hydraulic conductivity values for coarse sand fraction
4. Values of well bore storage constants deduced in this study agree with the characteristic of the model aquifer, given the test conditions,
5. Values of parameters determined for the model aquifer for different tests show that the aquifer was constructed using the same sand grain fractions,
6. The negative values of skin factors calculated in this study show that in all cases, the model wells were stimulated, which is quite consistent with the creation of the model aquifer-well system.
Acknowledgements
In preparing this manuscript, we acknowledge the immense support from the professor in charge of the newly installed ground water flow unit, Dr. Robert Jameson of the Department of Process Engineering and Applied Sciences of Dalhousie University who permitted access to the equipment used in this research work. We also wish to acknowledge the support of the department engineer, Matt Kudjatt who made available the required sand aggregate for the model aquifer. The faculty of Engineering of Dalhousie University and Cape Breton University are also greatly acknowledged for their supports in diverse ways.
References
- Peng HY, Yeh HD, Yang SY (2002) Improved numerical evaluation of the radial groundwater flow equation. Adva Water Resour 25: 663-675.
- Moench AF, Prickett TA (1972) Radial flow in an infinite aquifer undergoing conversion from artesian to water table conditions. Water Resour Res 8: 494-499.
- Whitaker S (1986) Flow in porous media I: A theoretical derivation of Darcy's law. Transport in porous media 1: 3-25.
- Bouwer H (1989) The Bouwer and Rice slug test: an update. 27: 304-309.
- Chaudhry A (2004) Oil Well Testing Handbook.
- De swaan oa (1976) Analytic solutions for determining naturally fractured reservoir properties by well testing. SPE J 16: 117-122.
- Barrash W, Clemo T, Fox JJ, Johnson TC (2006) Field laboratory and modeling investigation of skin effect at wells with slotted casing, boise hydrogeophysical research site. J Hydro 326: 181-198.
- TurÄÂek P, Frankovská J, Súľovská M, Hulla J, kovac L, et al. (2013) Stability and dewatering Problems of Deep Excavations in Bratislava. pp: 2107-2110.
- Angel ML, Johnston S, O’Steen K, Brown CJ (2015) Groundwater Control Issues in Transportation Engineering: A Short Review of Dewatering Methods and Lessons Learned. 8 : 8-13.
- Sadeghpour AH, Ghanbari A, Fadaee M (2008) Groundwater Lowering in Deep Excavation (CaseStudy: Foundation Excavation of Shahid Madani Dam). pp: 1-5.
- Faulkner J (2008) Laboratory analog study of groundwater Flow and Solute Transport in a Karst Aquifer with Conduit and Matrix Domains.
- Faulkner J, Hu B, Kish S, Hua F (2009) Laboratory Analog and Numerical Study of Groundwater Flow and Solute Transport in a karst aquifer with conduit and matrix domains. J Cont Hydr 110: 34–44.
- Öllõs G, Szakvélemény NE (1960) Study of the Physical Modeling of the Flow Processes in Fractured Rock.
- Öllõs G (1964) An Investigation into Hydraulic Phenomena in Karstic Systems. 44: 21–28.
- Mortensen J, Fabricius IL, Engtrom F (1998) The relation among porosity, permeability and specific surface of chalk from the Gorm Field, Danish North Sea. SPE Reser Eva Eng 3: 245-251.
- Knoll MD, Knight R, Brown E (1995) Can Accurate Estimates of Permeability be Obtained From Measurement of Dielectric Properties? pp: 25-35.
- Bear J (1972) Dynamics of Flyuid in Porous Media pp: 784.
- Scheidegger A (1974) The physics of flow through porous media. Univ of Toronto Press.
- Kozeny J (1927) Ueber kapillare leitung des wassers im Boden: Sitzungsber Acad Wiss Wien 136: 271-306.
- Carmen P (1965) Flow of Gases Through Porous Media. pp: 182.
- Yin H (1993) Acoustic velocity and attenuation of rocks.
- Barlow PM, Moench AF (1999) A computer program for calculating drawdowns and estimating hydraulic properties for confined and water-table aquifers. Water-Resour Invest Rep: 99-4225.
- Mercer JW, Faust CR (1980) Ground water Modeling-Mathematical Models 18: 212-222.
- Tolikas P, Sidiropoulos E, Tzimopoulo C (1984) A simple analytical solution for the boussinesq one-dimensional groundwater flow equation. Water Resour Res20: 24-28.
- Danesfaraz R, Kaya BA (2009) Numerical solution of the one dimensional groundwater flow by transfer matrix method. J Sci Tech 3: 161-164.
- Saffi Y (2014) Analytic solution to a one-dimensional leaky and heterogeneous transient Aquifer mode. Hydro Sci J 59 : 138-153.
- Loáiciga HA (2009) Derivation Approaches for the Theis (1935) Equation. NGWA 48 : 2-5.
- Agarwal R, Al-Hussainy R, Ramey HJ (1970) An investigation of wellbore storage and skin effect in unsteady liquid flow, 1. Analytical treatment. SPE 249: 279-290.
- Chen CS, Chang CC (2003) Well hydraulics Theory and Data Analysis of the Constant Head Test. Water Resour Res 39: 7-14.
- Duffield GM (1989) AQTESOLVE.
- Lafata L (2014) Effect of Particle Shape and Size on Compressibility Behavior of Dredged Sediment in a Geotextile Tube Dewatering Application.
- Liu P, Li W, Xia J (2016) Derivation and application of mathematical model for well test analysis with variable skin factor in hydrocarbon reservoirs. AIP Adv 6: 1-10.
- Earlougher JC, Kersch KM (1974) Analysis of Short-Time Transient Test Data By Type-Curve Matching. JPT: 793-800.
- Okuda K, Morita J, Shinjuku-ku (1984) Patent No. United States Patent.
- Wentworth C (1922) A scale of grade and classterms for clastic sediments. The Journal of Geology 30(5): 377-392.
- Rock Mechanics IS (1977) Suggested Methods for Determining Water Content, Porosity, Density, Absorption and Related Properties and Swelling and Slake-Durability Index Properties.
- Nardone JP (2009) Well Testing Project Management.
- Alden A (2019) All About Sediment Grain Size.
- Domenico P, Schwartz F (1990) Phys Chem Hydro.
- Mavis FT, Wisely EF (1936) A Study of the Permeability of Ottawa Sand. University of Iowa.
- Park E, Zhan H (2002) Hydraulics of a finite-diameter horizontal well with wellbore storage and skin effect. Adv Water Resour 25: 389-400.
- Papadopoulos I, Cooper Jr H (1967) Drawdown in a well of large diameter. Water Resour Res: 241-244.
- Moench A (1985) Transient flow to a large-diameter well in an aquifer with storative semiconï¬Âning layers. Water Resour Res 21: 1121-1131.
- Wang C, Yeh H, Tsai C (2012) Transient drawdown solution for a constant pumping test iï¬Ânite two-zone conï¬Âned aquifers in ï¬Ânite two-zone conï¬Âned aquifers. Hydrol Earth Syst Sci 16: 441-449.
- Testwells (2016) Wellbore Storage.
- Cooper H, Jacob CE (1946) A generalized graphical method for evaluating formation constants and summerizing Ell field history. Am Geophy Union 27: 526-534.
- Mushila C, Otieno F, Ochieng G (2016) Hydraulic design to optimize the treatment capacity of multi-stage filtration units. Physics and Chemistry of the Earth Parts A/B/C. 92: 85-91.
- Kuan-Mu Yao (1971) Water and waste water filtration. Concepts and applications. Environ Sci Technol 5: 1105-1112.
- Agriculture US (1994) Chapter 26 Gradation Design of Sand and Gravel Filters.
- Fetter CW (2001) Applied Hydrogeology Fourth Edition.
- Sharp JM (1976) Momentum and energy balance equations for compacting sediments. Math Geo
- Beyer L, Clutsom F (1978) Density and Porosity of Oil Reservoir and Overlying Formation from Borehole Gravity Measurement.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi