Research Article, Res Rep Math Vol: 1 Issue: 1

A Simpler Proof of the Characterization of Quadric CMC Hypersurfaces in Sn+1

Aquino CP^1* and De Lima HF²

¹Department of Mathematics, Universidade Federal do Piaui, Teresina, Brazil

²Department of Mathematics, Universidade Federal de Campina Grande, Campina Grande, Paraiba, Brazil

*Corresponding Author : Aquino CP
Department of Mathematics, Universidade Federal do Piaui, Teresina, Brazil
Tel: (86) 3215-5525
E-mail: cicero.aquino@ufpi.edu.br

Received: August 10, 2017 Accepted: September 01, 2017 Published: September 07, 2017

Citation: Aquino CP, De Lima HF (2017) A Simpler Proof of the Characterization of Quadric CMC Hypersurfaces in Sⁿ⁺¹. Res Rep Math 1:1.

Abstract

Keywords: Euclidean sphere; Constant mean curvature hypersurfaces; Support functions; Totally umbilical hypersurfaces; Clifford torus

Introduction

In 2008, Alias, Brasil and Perdomo studied complete hypersurfaces immersed in the unit Euclidean sphere 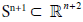, whose height and angle functions with respect to a fixed nonzero vector of the Euclidean space 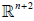are linearly related. Let us recall that, for a fixed arbitrary vector 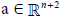the height and the angle functions naturally attached to a hypersurface 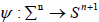endowed with an orientation ν are defined, respectively, by 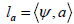and 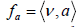In this setting, they showed the following characterization result concerning the quadric constant mean curvature hypersurfaces of Sⁿ⁺¹ [1,2]:

Theorem 1

Let 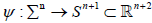be a complete hypersurface immersed in Sⁿ⁺¹ with constant mean curvature. l_a=λ f_a for some non-zero vector 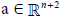and some real number λ, then Σⁿ is either a totally umbilical hypersurface or a Clifford torus 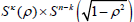, for some k = 0; 1;..; n and some k=0,1,…,n and ρ>0.

Later on, working with a different approach of that used in [2], the first and second authors characterized the totally umbilical and the hyperbolic cylinders of the hyperbolic space Hn+1as the only complete hypersurfaces with constant mean curvature and whose support functions with respect to a fixed nonzero vector a of the Lorentz- Minkowski space are linearly related (see Theorem 4:1 of [3,4], for the case that a is either space like or time like, and Theorem 4:2 of [5], for the case that a is a nonzero null vector). In this short article, our purpose is just to use a similar approach of that in [4,5] in order to present a new and more simple proof of Theorem 1 (cf. Section 3). For this, in Section 2 we recall some preliminaries facts concerning hypersurfaces immersed in Sⁿ⁺¹.

Preliminaries

Let 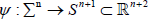be an orientable hypersurface immersed in the Euclidean sphere. We will denote by A the Weingarten operator of Σⁿ with respect to a globally defined unit normal vector ν.

In order to set up the notation, let us represent by ∇⁰ , ∇and ∇ the Levi-Civita connections of 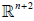, Sⁿ⁺¹ and Σⁿ respectively. Then the Gauss and Weingarten formulas for Σⁿ in Sⁿ⁺¹ are given, respectively, by

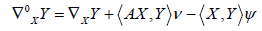
and

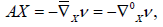
for all tangent vector fields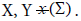

In what follows, we will work with the first three symmetric elementary functions of the principal curvatures λ₁,… λ_n of ψ, namely:

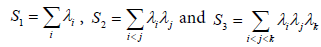
where i, j, k ∈ {1,…, n}.

As before, for a fixed arbitrary vector a 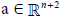let us consider the height and the angle functions naturally attached to which are defined, respectively, by 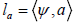and 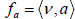. A direct computation allows us to conclude that the gradient of such functions are given by 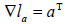and 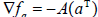, where a^Τ is the orthogonal projection of a onto the tangent bundle Τ Σ , that is,

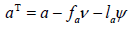
Taking into account that 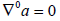and using Gauss and Weingarten formulas, we obtain 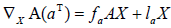for all 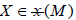. We use this previous identity jointly with Codazzi equation to deduce that

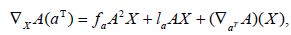
For all that 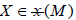Thus according to [6] (see also [3]), it follows from the last two identities that

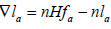(2.1)

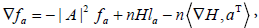(2.2)

where H = (1/n) S₁ is the mean curvature function of Σⁿ

For what follows, it is convenient to consider the so-called Newton transformation

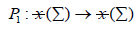
P₁= S₁-A

where I is the identity operator. Naturally associated with the Newton transformation P1, we have the Cheng-Yau’s square operator [7], which is the second order linear di erential operator 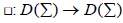given by

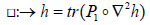(2.4)

Here 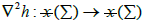stands for the self-adjoint linear operator metrically equivalent to the hessian of h, and it is given by

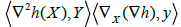
For all X, Y∈ x (Σ) .

Based on Reilly’s seminal paper [8-10], Rosenberg [6] showed the following idenfitities related to the action of on the functions l_a and f_a:

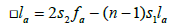(2.5)

And

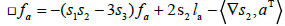(2.6)

To close this section, we quote a suitable Simons-type formula which can be found in [1] or [11].

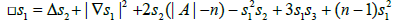(2.7)

Proof of Theorem

Now, we are in position to proceed with our alternative proof of Theorem 1.1. If λ=0 then l_a= λf_a=0, that is

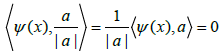
for all 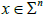and, consequently, Σⁿ is a totally umbilical sphere of Sⁿ⁺¹.

So, let us assume that λ≠0. We have Δla₌λΔfa _and using the fact that H is constant, from (2.1) and (2.2) we conclude that

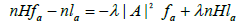
Or equivalently,

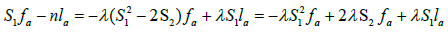
Hence, we get that

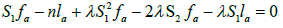(3.1)

By (3.1), we obtain

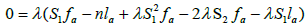
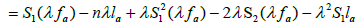
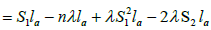
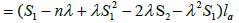
Thus,

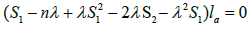(3.2)

We define a function

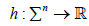by

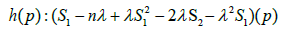
Suppose that h(p₀)≠0 for some p₀ ∈ Σⁿ Since h is smooth, there exists a neighbourhood u of p₀ in Σⁿ in which h(p)≠0 all p∈ u From (3.2) we conclude that l_a=0 in u and, hence f_a=0 in u. since λ≠0. we arrive at a contradiction because in Σⁿ we have

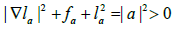
Therefore, h = 0 on Σⁿ, that is,

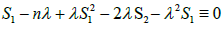(3.3)

Consequently, S₂ is constant on Σⁿ . Repeating the previous argument for the operator L₁ and using the fact that S₂ is constant, we also obtain that

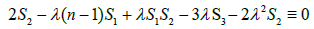(3.4)

We observe that the above equation shows that S₃ is also constant on Σⁿ . We also note that this argument shows, in fact, that S_r is a constant function on Σⁿ for all 2≤r≤n. From (2.7) we get

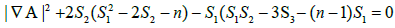
More precisely,

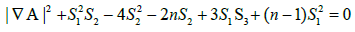(3.5)

We observe that if H=0, then S1=0 and, consequently, |A|²=−2s₂ From (3.3), we have 2S₂ =−n and |A|₂ = n. Therefore, since

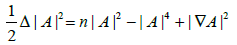
We have that 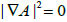and, hence, from Theorem 4 of [9], we conclude that Σⁿ must be a Clifford torus

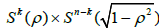, for some k=0,1,…,n and some ρ>0.

Now, suppose that H≠0 By equation (3.4) we get

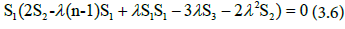
that is,

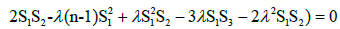(3.7)

From equation (3.5) we have

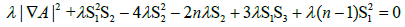(3.8)

Furthermore, from a straightforward computation we can verify that

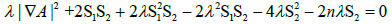(3.9)

Hence, if S₂ = 0 we obtain of (3.9) that 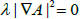consequently, |∇A|² =0 and, since Σⁿ is complete, it follows once more from Theorem 4 of [9] that Σⁿ must be a Clifford torus.

If S₂≠0 then 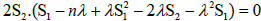implies

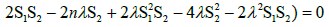(3.10)

We note that (3.10) and (3.9) imply 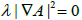and, hence, repeating the previous argument we also get that Σⁿ is a Clifford torus. Therefore, we conclude the proof of Theorem 1.

References

1. Alencar H, do Carmo M, Colares G (1993 )Stable hypersurfaces with constant scalar curvature. Math Z 213: 117-131.
2. Alias LJ, Brasil Jr A, Perdomo O (2008) A characterization of quadratic constant mean curvature hypersurfaces of spheres. J Geom Anal 18: 687-703.
3. Alias LJ, Dajczer M (2006) Uniqueness of constant mean curvature surfaces properly immersed in a slab. Comment Math Helv 81: 653-663.
4. Aquino CP, de Lima HF (2012) On the Gauss map of complete CMC hypersurfaces in the hyperbolic space, J Math Anal Appl 386: 862-869.
5. Aquino CP, de Lima HF (2014) On the geometry of horospheres. Comment Math Helv 89: 617-629.
6. Rosenberg H (1993) Hypersurfaces of constant curvature in space forms. Bull Sc Math 117: 217-239.
7. Cheng SY, Yau ST (1977) Hypersurfaces with constant scalar curvature. Math Ann 225: 195-204.
8. Garding L (1959) An inequality for hyperbolic polynomials. J Math Mech 8: 957-965.
9. Lawson HB (1969) Local rigidity theorems for minimal hypersurfaces. Ann Math 89: 187-197.
10. Reilly RC (1973) Variational properties of functions of the mean curvature for hypersurfaces in space form. J Di Geom 8: 447-453.
11. Caminha (2006) On hypersurfaces into Riemannnian spaces of constant sectional curvature. Kodai Math J 29: 185-210.