Research Article, J Hydrogeol Hydrol Eng Vol: 9 Issue: 5
A Strategy for Calibration and Validation of a Physically Based Distributed Hydrological Model in Tropical Catchments: Case Study of São Paulo, Brazil
Lara Gabrielle Garcia1*, Aline Aparecida Fransozi2, Diana Yulieth Peña Sierra2, Patrick Lane3 and Silvio Frosini de Barros Ferraz21 Forest Science Department, Forestry Science and Research Institute, Av. Comendador Pedro Morganti, Piracicaba, Brazil
2 Forest Science Department, University of São Paulo (USP), São Paulo, Brazil
3 Forest Science Department, University of São Paulo (USP), São Paulo, Brazil
*Corresponding Author : Lara Gabrielle Garcia
Forestry Science and Research
Institute, Av. Comendador Pedro Morganti, Piracicaba, Brazil
Tel: (+55)
019982151254
E-mail: lara@ipef.br
Received date: November 19, 2020; Accepted date: November 04, 2020 Published date: December 11, 2020
Citation: Garcia LG, Fransozi AA, Peña Sierra DY, Lane P, de Barros Ferraz SF (2020) A Strategy for Calibration and Validation of a Physically Based Distributed Hydrological Model in Tropical Catchments: Case Study of São Paulo, Brazil. J Hydrogeol Hydrol Eng 9:4.
Abstract
Hydrological modeling is an important tool for water resources planning, and calibration and validation are one of the main steps for the right use of models. The intrinsic characteristics of the tropical region, such as temperature, precipitation and soils, require special attention in the modeling processes to increase simulation accuracy of physically based distributed models. In this paper we describe and analyze calibration and validation steps of these models to understand the challenges of hydrological modeling in the tropical region. A catchment located in the tropical region was used for the calibration and validation of a physically based distributed hydrological model (Mike SHE). The results showed that the saturated zone has a fundamental role in the hydrological responses, mainly for the minimum flow simulations; however, the land use parameters results in low influence on the annual flow. Adjustments of maximum flow in tropical regions seem to be more influenced by intensity of precipitation. Therefore, the results suggest that the strategy of fitting the base flow followed by the adjustment of the maximum flow and the evapotranspiration and transpiration processes is an efficient procedure to calibrate the model.
Keywords: Distributed hydrological model; Parameter model; Sensitivity analysis; Manual calibration
Introduction
Hydrological models are important tools to assist the management of water resources [1] and for land use planning when the goal is to quantify the availability of hydrological services [2,3], by simulating hydrological indicators based on future scenarios [4,5]. However, the reliability of simulation information depends on an important step in the modeling processes: the calibration and validation of the models with data observed in the field.
The aim of model calibration and validation is to increase the accuracy between observed and simulated data, and, consequently, decrease the errors and prediction uncertainties [6,7]. Physically based distributed hydrological models require a high number of parameters and input information, which increases the time of parameterization stage for these models [8,9].
It has been argued that calibration and validation of such models require particular attention when used in tropical systems [10,11], as critical hydrological process interactions may differ significantly from those in temperate regions, where most of the models are structured [12,13].
In terms of these process/response differences, perhaps the most significant are high precipitation, high temperatures, and highly weathered soils [14]. Precipitation is far higher, both in volume and intensity, than in temperate zones; up to 40% of events may be classified as high intensity, whereas in temperate areas they represent only 5% [15]. Tropical soils also have different characteristics, as a function of the precipitation regime and high temperatures, vegetation type, organic matter content, among other factors, resulting in accelerated physical and biological processes in soils [13,16]. Thus, in the tropical zone, it is common to find soils with a high degree of weathering, which results in greater soil depth and a higher proportion of clay [17]. The intrinsic characteristics of the region can modify the processes and the way the models simulate them in other systems [18].
We argue that to understand the hydrological functioning of tropical systems and to model the dynamics of land use in these systems, physically based distributed hydrological models are an important research tool. Thus, the objectives of this study were to describe and analyze the calibration and validation steps of a physically based distributed hydrological model and understand the uncertainties and challenges of the modeling process in the tropical region.
Materials and Methods
Study area
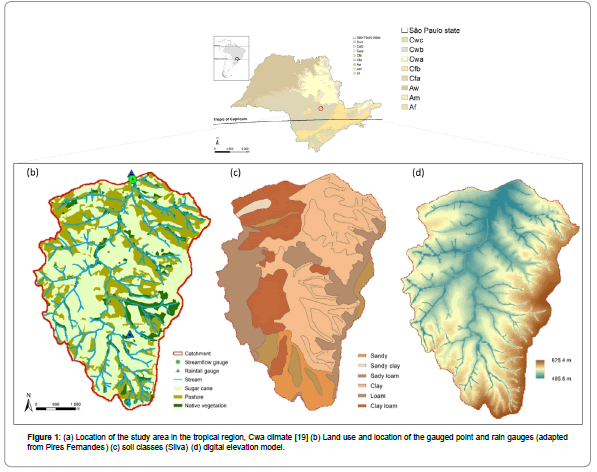
Calibration and validation (C&V) of the hydrological model was performed in a catchment (2,194.8 ha) located in the tropical region, in the state of São Paulo, Brazil (Figure 1). The local climate is Cwa with rainfall concentrated in the summer and dry winter [19], characterizing a high seasonality of precipitation and elevated temperatures.
Precipitation (P) was measured with two rain gauges located in the catchment. The streamflow (Q) and precipitation datasets used in this study correspond to the period from 1999 (P=1219 mm, Q=469.5 mm) to 2000 (P=1296 mm, Q=405.7 mm). Although two year could be a short period for calibration and validation processes, it was used a hot start period of three months before calibration period for warn-up the model [20,21]. Reference evapotranspiration was calculated using the FAO modified Penman-Monteith method [22]. The land use class was divided into: sugar cane, (1,273.9 ha, 58%); pasture (731 ha, 33%); and native vegetation (186.5 ha, 9%). The soil type characterization used was obtained on a 1:20.000 scale [23,24] and categorized by texture: clay (42%), clay loam (21%), sandy clay (1%), loam (6%), sandy (7%) and sandy loam (23%).
The calibration and validation present (1999 and 2000) represents typical years considering precipitation, streamflow and evapotranspiration variables.
Model code and parameterization
In this work, the C&V process was carried out using the physically based distributed hydrological model MIKE SHE [25,26]. A detailed description of the modeling methods can be found in Abbott et al. [25,27] and DHI [28,29].
Supplementary material
Here we present all the parameters used in calibration and validation stages discussed in the paper. Soil parameters values measured in the field (Table 1); land use parameters (Table 2); surface roughness and river bed resistance (Manning’s number) (Table 3); evapotranspiration actual and overland flow processes (Table 4).
| Soil texture | Area | K0 | α | m | n | l | |
|---|---|---|---|---|---|---|---|
| ha | % | mm h-1 | 1 cm-1 | - | - | - | |
| Clay A | 909,2 | 42,0 | 7,3 | 0,018 | 0,413 | 1,703 | 0,5 |
| Clay B | 7,3 | 0,018 | 0,413 | 1,703 | 0,5 | ||
| Clay loam A | 439,7 | 20,3 | 33,2 | 0,024 | 0,459 | 1,853 | 0,5 |
| Clay loam B | 11,6 | 0,024 | 0,448 | 1,811 | 0,5 | ||
| Sandy clay A | 23,4 | 1,1 | 74,2 | 0,049 | 0,449 | 1,816 | 0,5 |
| Sandy clay B | 17,3 | 0,017 | 0,414 | 1,705 | 0,5 | ||
| Loam A | 137,9 | 6,4 | 20,4 | 0,033 | 0,389 | 1,641 | 0,5 |
| Loam B | 20,4 | 0,033 | 0,389 | 1,641 | 0,5 | ||
| Sandy A | 160,1 | 7,4 | 6,0 | 0,009 | 0,398 | 1,661 | 0,5 |
| Sandy B | 6,0 | 0,009 | 0,398 | 1,661 | 0,5 | ||
| Sandy loam A | 496,7 | 22,9 | 16,4 | 0,022 | 0,449 | 1,816 | 0,5 |
| Sandy loam B | 5,7 | 0,016 | 0,370 | 1,587 | 0,5 | ||
Table 1: Soil parameters values for soil classes in two layers (A=surface and B=subsurface); K0=saturated hydraulic conductivity; α, m and n are van Genutchen parameters [31]; and l=shape factor.
| Day | LAI(1) | Kc(2) | RD(3) | LAI(1) | Kc(4) | RD(4) | LAI(1) | Kc(4) | RD(5) |
|---|---|---|---|---|---|---|---|---|---|
| m2 m-2 | - | mm | m² m-2 | - | mm | m2 m-2 | - | mm | |
| Sugar cane | Pasture | Native vegetation | |||||||
| 31 | 1,61 | 1,13 | 1.914 | 1,7 | 0,75 | 1 | 3,8 | 1,0 | 7 |
| 61 | 1,71 | 1,15 | 2.471 | 1,6 | 0,75 | 1 | 4,1 | 1,0 | 7 |
| 92 | 1,76 | 1,17 | 3.029 | 2,2 | 0,75 | 1 | 3,4 | 1,0 | 7 |
| 122 | 1,77 | 1,18 | 3.586 | 1,5 | 0,75 | 1 | 3,0 | 1,0 | 7 |
| 153 | 1,89 | 1,20 | 4.143 | 1,8 | 0,75 | 1 | 2,8 | 1,0 | 7 |
| 184 | 2,15 | 0,95 | 4.7 | 1,9 | 0,75 | 1 | 2,5 | 1,0 | 7 |
| 212 | 0,00 | 0,00 | 0 | 1,5 | 0,75 | 1 | 3,0 | 1,0 | 7 |
| 243 | 0,33 | 0,50 | 200 | 0,9 | 0,75 | 1 | 2,3 | 1,0 | 7 |
| 273 | 0,66 | 0,80 | 300 | 1,1 | 0,75 | 1 | 2,4 | 1,0 | 7 |
| 304 | 0,59 | 1,00 | 500 | 1,0 | 0,75 | 1 | 2,8 | 1,0 | 7 |
| 334 | 0,87 | 1,10 | 800 | 0,9 | 0,75 | 1 | 3,7 | 1,0 | 7 |
| 365 | 1,38 | 1,12 | 1.357 | 1,3 | 0,75 | 1 | 3,9 | 1,0 | 7 |
| Note: (1) [32]; (2) [33]; (3) [34]; (4) [35]; (5) [36] | |||||||||
Table 2: Parameters value used to characterize land use in catchment study. LAI: Leaf Area Index; Kc: Crop Coefficient; RD: Root Depth.
| Land use | Soil classes | M |
|---|---|---|
| m-1/3 s-1 | ||
| Native vegetation1 | Oxisols | 7 |
| Ultisols | 15 | |
| Inceptisols | 25 | |
| Entisols | 32 | |
| Pasture1 | Oxisols | 13 |
| Ultisols | 24 | |
| Inceptisols | 34 | |
| Entisols | 42 | |
| Sugar cane1 | Oxisols | 7 |
| Ultisols | 17 | |
| Inceptisols | 27 | |
| Entisols | 34 | |
| River bed resistance2 | 28 | |
| Note: (1) [30]; (2) [37] | ||
Table 3: Parameter values of Manning’s number (M).
| Process | Parameters | Unit | Land use | |||
|---|---|---|---|---|---|---|
| Uniform | Native vegetation | Pasture | Sugar cane | |||
| Evapotranspiration actual (ETR) | CINT | mm | 0,5 | - | - | - |
| C1 | - | 0,3(1) | - | - | - | |
| C2 | - | 0,2(1) | - | - | - | |
| C3 | mm day-1 | 30(4) | - | - | - | |
| AROOT | 1 m-1 | 0,1(1) | - | - | - | |
| Overland flow | S | mm | - | 5(2) | 2(3) | 2(3) |
| Note:(1) [28]; (2) [39]; (3) [40]; (4) [41] | ||||||
Table 4: Parameters values used to model evapotranspiration actual and overland flow processes (CINT: canopy interception storage; C1, C2 e C3: Evapotranspiration coefficients of [38]; AROOT: root distribution; S: detention storage).
The values of the soil water retention curve and saturated hydraulic conductivity (K0) was measured in the field [30] and are presented in Table 1. Previous studies were used to characterize the three land uses present in the catchment. Vegetation parameters such as Leaf Area Index (LAI), Root Depth (RD) and crop coefficient (Kc) were distributed over time (Table 2). The surface roughness (M) was distributed in terms of land use and soil type (Table 3). Detention storage (S) and the evapotranspiration parameters (interception coefficient – Cint, C1, C2, C3 and AROOT) were distributed according to land use (Table 4).
The water flux between the Saturated Zone (SZ) and river depends on the leakage coefficient (LeakCoef) [28], and was given an initial value of 1.10-3 s-1 that corresponds to minimum flow in the catchment (Q99).
Horizontal and vertical hydraulic conductivity was measured in the field [30], and its value (9.44E-8 m s-1) was considered uniform. In the same way, uniform values of specific yields (SY=0,2) and specific storage (SS=1.10-4 L-1) were used. Efficiency criteria used to evaluate the C&V performance was presented in Table 5.
Calibration and validation procedure
Calibration steps: The sensitivity analysis (SA) was carried out as the maximum absolute ratio of variation of three variables (hydrological indicators derived from the flow duration curve): annual streamflow (Q), maximum flow (Q5), and minimum flow (Q70-99). Thirteen parameters were selected to quantify the sensitivity: horizontal hydraulic conductivity (Kx), vertical hydraulic conductivity (Ky), saturated hydraulic conductivity (K0), surface retention (S), Manning’s number (M); Manning’s number for channel (M_channel), leakage coefficient (LeakCoef), interception coefficient (Cint), Leaf Area Index (LAI), evapotranspiration coefficients (C1, C2 and C3) and root distribution (AROOT) [45].
The C&V process was based on the manual method. Regarding the parameter adjustment stage, we proposed a three-part approach: optimization of minimum flow, optimization of maximum flow and optimization of the hydrological process (actual evapotranspiration ETR and interception-INT).
Comparative analyses
The efficiency of C&V performance was evaluated in three ways: visual (analysis of flow duration curves – FDC), relative (relationship between observed and simulated data) [42,44] and by efficiency criteria: Nash-Sutcliffe (NSE), Nash-Sutcliffe for minimum flows (NSE_base); modified Kling-Gupta (KGE’); and percent bias (PBIAS). Details of the efficiency criteria functions can be found in Table 5-SM.
Results
Calibration steps
The sensitivity analysis (SA) results showed that horizontal hydraulic conductivity (Kx) had large influence on annual flow (Q) and minimum flow (Q70-99) (34.4% and 134.4%, respectively), while the LeakCoef had a sensitivity of 0.2% for Q70-99. Saturated hydraulic conductivity (K0) and M-Channel were highlighted as the most sensitive to maximum flow (Q5), followed by M, S and Ky. Looking at the ETR and INT process, the Cint influenced the annual flow by 0.8%.
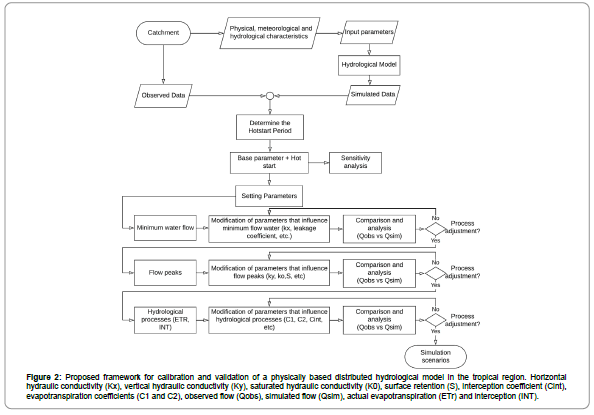
The steps used in minimum and maximum flow optimization and hydrological processes followed the framework proposed in Figure 2, where the phases for the C&V of a model are described, considering the better approach to obtain the efficiency indexes required for adjustments.
Figure 2: Proposed framework for calibration and validation of a physically based distributed hydrological model in the tropical region. Horizontal hydraulic conductivity (Kx), vertical hydraulic conductivity (Ky), saturated hydraulic conductivity (K0), surface retention (S), interception coefficient (Cint), evapotranspiration coefficients (C1 and C2), observed flow (Qobs), simulated flow (Qsim), actual evapotranspiration (ETr) and interception (INT).
Warm-up and hot start
In the early stages of C&V process, a hot start of three months was obtained for warm up of the model aiming to avoid biased results. The base simulation, with initial parameters and a hot start, overestimated the annual flow by 17.4% compared to observed data, and the minimum flows were the most overestimated (582%).
Optimization of minimum and maximum flows
The parameters Kx (4.7 × 10-7 m s-1) and LeakCoef (10-9 s-1) were modified for adjustments in minimum flows, and these changes showed lower differences between observed and simulated data for Q90 (difference of 13.8%). Besides, the efficiency indexes NSE_BASE (0.65) and KGE’ (0.76) reached the minimum suitable values for model calibration after these changes. Once the best fit for minimum flow is obtained, the values of calibrated parameters were maintained until the final step of calibration.
After the adjustments of minimum flows, the Q5 was underestimated by 6.3%. The initial value of the S parameter (1.5 mm) was reduced and the initial value of M_Channel (43 m-¹/3 s-¹) was increased aiming to raise the speed and volume of surface runoff. The changes in S value decrease to 5.2% the difference between observed and simulated maximum flows, and to 0.7% the relative difference between annual flows. The efficiency indexes remained equal, except PBIAS, which decreased to 0.71%.
Optimization of the hydrological processes
After the adjustments of maximum and minimum flows, the ETR was 67% of the annual precipitation, and the interception process was about 6.1%. The parameter Cint (1.5 mm) was modified aiming to increase the interception. This change increased the interception to 13.3%, while the results of evapotranspiration showed a slight increase (from 67% to 68%). However, when analyzed for each soil use, we can see that the larger percentages of ETR follow the differences in land use (native vegetation=86%; sugarcane=67%; pasture=58%). Therefore, this new value of Cint was maintained in the model for future simulations.
Calibration and validation processes
With all adjustments completed, the calibration (year 1999) and validation (year 2000) indexes were obtained (Table 6). The simulated flow was underestimated both in calibration and in validation (-2.2% and -4.7%, respectively). Corroborating these data, the efficiency indexes were within the accepted range to consider the model efficient in predicting scenarios, with errors at 2% in calibration and 5% in validation.
| Steps | Modified parameters | Efficiency index | ||||||
|---|---|---|---|---|---|---|---|---|
| Kx | LeakCoef | S | Cint | NSE | NSE_BASE | KGE' | PBIAS | |
| m s-1 | s-1 | mm | mm | |||||
| Calibration | 4.7 × 10-7 | 10-Sep | 1.5 | 1.5 | 0.56 | 0.66 | 0.76 | 2.21 |
| Validation | 4.7 × 10-7 | 10-Sep | 1.5 | 1.5 | 0.6 | 0.64 | 0.78 | 4.71 |
| Abbreviations: Kx: horizontal hydraulic conductivity parameter; LeakCoef: Leakage Coefficient; S: surface retention parameter; Cint: Interception Coefficient; NSE: Nash-Sutcliffe Efficiency Index; NSE_BASE: Adaptation of Nash-Sutcliffe Efficiency Index for Base Flow; KGE’: modified Kling-Gupta Efficiency index; PBIAS: Bias of Data in Percentage. | ||||||||
Table 6: Results of efficiency indexes and total flow for calibration (year 1999) and validation (year 2000).
Discussion
Calibration and validation process
With respect to the first research question, sensitivity analysis (SA), the changes in the Kx parameter resulted in the highest sensitivity of the annual flow (34.4% sensitivity), which may be related to the importance of the saturated zone in the distributed models [25]. The influence of Kx on minimum flows was observed in the current study, highlighting the importance of this parameter in the C&V steps [46]. It was found that there is a direct relationship between the Kx parameter and the annual flow and flow base in the tropical region.
On the other hand, Q5 did not show high sensitivity to changes in Kx (2.5% of sensitivity) as occurs in the temperate region [47]. This result may be explained by the characteristics of tropical soils [48]: deeper soils can reduce the influence of the saturated zone on the peak flow because water table in these soils is deeper. Therefore, the variable Q5 could be more influenced by the intensity of precipitation than by the proximity of the water table.
Warm-up and hot start
In this study, warming up the model to start the calibration process allowed initial soil conditions to become more similar to the observed ones, since model warm-up plays an important role in adjusting hydrological processes [49]. This adjustment is an important step in the modeling of tropical catchments, since in this region, there are soils with higher clay content [17] and deep soils [50]. Overall, it is important that the initial conditions were adjusted before the period considered for C&V.
Optimization of minimum flow
In relation to the C&V processes for optimization of minimum flows, the first parameter adjusted was Kx, as it is an important parameter for the regulation of the saturated zone, and these results are in line with those of previous studies [51,52]. Modifying Kx was sufficient to reduce the relative difference in both the minimum flow index (from 582% to 191%) and the annual flow (from 17.4% to -0.8%). The decrease in leakage coefficient resulted in a lower minimum flow index and better NSE_BASE index (from 0.3 to 0.6). This improvement in the efficiency indexes showed that adjusting minimum flow is fundamental in the C&V process, since its adjustment allowed a considerable gain in the efficiency indexes.
This relation of leakage coefficient and minimum flows in the tropical region may be related to the importance of the saturated zone in this region, because of the characteristics of deeper soils, more intense rainfall and seasonality of rain [13]. These results highlight the saturated zone as an important compartment in the C&V processes.
Optimization of maximum flow
The change in the S parameters resulted in better efficiency indexes; however, in other C&V procedures carried out in temperate zone systems these gains had even better results in the calibration of the peak flow than those found in this study [53]. Adjusting the peak flow rates after the minimum flow rates was efficient in this case, since few changes occurred with changes in land use parameters.
The adjustment of peak flows seems to be directly related to the intensity of precipitation. In intense precipitation, changes in land use parameters show low sensitivities in C&V processes [54]. Thus, the intensity of precipitation seems to be a more important variable in modeling in the tropical region.
Optimization of hydrological processes
After the adjustments in the minimum and maximum flow index, the efficiency indexes had already reached a satisfactory C&V value. However, when analyzing the interception and actual evapotranspiration processes, adjustments were still necessary. The simulated interception was 6.1% and the values measured in this catchment vary from 14% to 24% of the precipitation [55,56]. The need for adjusting the empirical parameters of hydrological process during calibration can be explained by the difference in climate and soil features between the region where methods are adjusted (temperate) and the region where we are simulating (tropical). For example, for a C&V process in temperate zone, the authors consider the influence of Cint parameters negligible on the final results [52], or without significant effect on the results [57]. On the other hand, a study in tropical zone shows that change in vegetation parameters (C1, C2 and Cint) produced better results [41].
Thus, especially when the focus is on the hydrological processes that are taking place in the scenarios, it is important to check not only the efficiency indexes of the models, but also the simulated hydrological processes, since the hydrological models were adjusted in regions with different characteristics of soil and precipitation.
Model limitation for tropical region
In this study, the C&V process was efficient to fit observed and simulated flows and could be considered acceptable; however, since it is a manual calibration, the interrelationships between the parameters remain as sources of options not fully explored, as they depend on an automatic calibration [58,59].
As it is one of the most important inputs, the quality of the precipitation data is proportional to the quality of the calibration [60,61], particularly in the tropical region with more intense and seasonal precipitation [62]. In the present study, the presence of only two rainfall gauges may not have been sufficient for accurately representing precipitation [58,63].
One of the greatest difficulties encountered was that our model consistently overestimated the minimum flow, and this model limitation has been reported in other studies [64]. This was more frequent in dry periods, in which the model often overestimated the minimum values [64-66].
Conclusion
The calibration and validation processes of a hydrological model in the tropical region show that the saturated zone has a predominant influence on this process, mainly on the responses of the minimum flows. Concerning peak flow adjustments in tropical regions, the intensity of precipitation plays a fundamental role. For a suitable calibration and validation step, it is necessary to adjust the simulated hydrological processes, such as evapotranspiration and interception. Due to this influence, the strategy of following a sequence of adjustments, starting from minimum flows, followed by maximum flows and hydrological processes, showed to be an efficient procedure to calibrate the model.
Acknowledgement
This work was supported by the Brazilian federal agency for support and evaluation of graduate education (CAPES).
References
- Zégre N, Skaugset AE, Som NA, McDonnell JJ, Ganio LM (2010) In lieu of the paired catchment approach: Hydrologic model change detection at the catchment scale. Water Resour Res 46: 1-20.
- Birkel C, Soulsby C, Tetzlaff D (2012) Modelling the impacts of land-cover change on streamflow dynamics of a tropical rainforest headwater catchment. Hydrol Sci J 57: 154-1561.
- Guswa A, Brauman K, Brown C, Hamel P, Keeler B et al. (2014) Ecosystem services: Changes and opportunities for hydrologic modeling to support decision making. Water Resour Res 1-10.
- Marhaento H, Booij MJ, Hoekstra AY (2018) Hydrological response to future land-use change and climate change in a tropical catchment. Hydrol Sci J 63: 1368-1385.
- Wijesekara GN, Gupta A, Valeo C, Hasbani JG, Qiao Y et al. (2012) Assessing the impact of future land-use changes on hydrological processes in the Elbow River watershed in southern Alberta, Canada. J Hydrol 412-413: 220-232.
- Engel B, Storm D, White M, Arnold J, Arabi M (2007) A hydrologic/water quality model application protocol. J Am Water ResourAssoc 43: 1223-1226.
- Yuan Y, Khare Y, Wang X, Parajuli PB, Kisekka I et al. (2015) Hydrologic and water quality models: sensitivity. T ASABE 58: 1721-1744.
- Refsgaard JC, Storm B (1990) Construction, calibration and validation of hydrological models. In: Abbott MB, Refsgaard JC eds Distrib. Hydrol Model Springer Dordrecht pp: 41-54.
- Refsgaard JC (1997) Parameterisation, calibration and validation of distributed hydrological models. J Hydrol 198: 69-97.
- Boyero L, Ramírez A, Dudgeon D, Pearson RG (2009) Are tropical streams really different? J NAm Benthol Soc 28: 397-403.
- Taniwaki RH, Piggott JJ, Ferraz SFB, Matthaei CD (2017) Climate change and multiple stressors in small tropical streams. Hydrobiologia 793: 41-53.
- Gücker B, BoËchat IG, Giani A (2009) Impacts of agricultural land use on ecosystem structure and whole-stream metabolism of tropical Cerrado streams. Freshw Biol 54: 2069-2085.
- Wohl E, Barros A, Brunsell N, Chappell NA, Coe M et al. (2012) The hydrology of the humid tropics. Nat Clim Change 2: 655-662.
- Pascale S, Lucarini V, Feng X, Porporato A, Hasson S ul (2015) Analysis of rainfall seasonality from observations and climate models. Clim Dyn 44: 3281-3301.
- Hudson N (1982) Conservación del suelo. Barcelona, Editorial Reverté S.A.
- Buringh P (1981) Introduction to the study of soils in tropical and subtropical regions. Soil Sci 131: 66.
- Minasny B, Hartemink AE (2011) Predicting soil properties in the tropics. Earth-Sci Rev 106: 52-62.
- Beskow S, Norton LD, Mello CR (2013) Hydrological prediction in a tropical watershed dominated by oxisols using a distributed hydrological model. Water Resour Manag 27: 341-363.
- Alvares CA, Stape JL, Sentelhas PC, De Moraes Gonçalves JL, Sparovek G (2013) Köppen’s climate classification map for Brazil. Meteorol Z 22: 711-728.
- Daggupati P, Pai N, Ale S, Zeckoski RW, Jeong J et al. (2015) A recommended calibration and validation strategy for hydrologic and water quality models. T ASABE 58: 1705-1719.
- malone rw, yagow g, baffaut c, gitau mw, qi z et al. (2015) Parameterization guidelines and considerations for hydrologic models. T ASABE 58: 1681-1703.
- Allen RG, Pereira LS, Raes D, Smith M (1998) FAO Irrigation and drainage Paper No.56. Rome, FAO.
- Ranieri SBL, Sparovek G, Souza MP, Dourado Neto D (1998) Aplicação de índice comparativo na avaliação do risco de degradação das terras. Rev Bras Ciênc Solo 22: 751-760.
- Teramoto ER, Lepsch IF, Vidal-Torrado P (2001) Relações solo, superfície geomórfica e substrato geológico na microbacia do ribeirão Marins (Piracicaba - SP). Sci Agric 58: 361-371.
- Abbott M, Bathurst J, Cunge J, O’Connell P, Rasmussen J (1986) An introduction to the European Hydrological System—Systeme Hydrologique Europeen,“SHE”, 1: History and philosophy of a physically-based, distributed modelling. J Hydrol 87: 45-59.
- Vázquez RF, Feyen L, Feyen J, Refsgaard JC (2002) Effect of grid size on effective parameters and model performance of the MIKE-SHE code. Hydrol Process 16: 355-372.
- Abbott M, Bathurst J, Cunge J, O’Connell P, Rasmussen J (1986) An introduction to the European hydrological system — systeme hydrologique Europeen, “SHE”, 2: Structure of a physically-based, distributed modelling system. J Hydrol 87: 61-77.
- DHI (2016) Mike SHE - Volume 1: User guide. Hørsholm, Denmark.
- DHI (2016) Mike SHE - Volume 2: Reference guide. Hørsholm, Denmark.
- Mingoti R (2012) Efeitos da espacialização da cobertura florestal e da profundidade dos solos na produção de água de uma bacia hidrográfica. Univesidade de São Paulo
- van Genuchten MT (1980) A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci Soc Am J 44: 892–898.
- Xavier AC, Vettorazzi CA (2004) Mapping leaf area index through spectral vegetation indices in a subtropical watershed. Int J Remote Sens 25: 1661–1672.
- Monteiro LA, Sentelhas PC (2014) Potential and actual sugarcane yields in southern Brazil as a function of climate conditions and crop management. Sugar Tech 16: 264–276.
- Battie Laclau P, Laclau JP (2009) Growth of the whole root system for a plant crop of sugarcane under rainfed and irrigated environments in Brazil. Field Crops Research 114: 351–360.
- Allen RG, Pereira LS, Raes D, Smith M (1998) FAO Irrigation and drainage paper No.56. Rome, FAO.
- Canadell J, Jackson R, Ehleringer J, Mooney HA, Sala OE et al. (1996) Maximum rooting depth of vegetation types at the global scale. Oecologia 108: 583–595.
- Chow V te (1959) Open-channel hydraulics.
- Kristensen KJ, Jensen SE (1975) A model for estimating actual evapotranspiration from potential evapotranspiration. Nordic Hydrology 6: 170–188.
- Jayatilaka CJ, Storm B, Mudgway LB (1998) Simulation of water flow on irrigation bay scale with MIKE-SHE. J Hydrol 208: 108–130.
- Wang S, Zhang Z, Sun G, Strauss P, Guo J et al. (2012) Multi-site calibration, validation, and sensitivity analysis of the MIKE SHE Model for a large watershed in northern China. Hydrol Earth Syst Sci 16: 4621–4632.
- Sahoo GB, Ray C, De Carlo EH (2006) Calibration and validation of a physically distributed hydrological model, MIKE SHE, to predict streamflow at high frequency in a flashy mountainous Hawaii stream. J Hydrology 327: 94–109.
- Thirel G, Andréassian V, Perrin C, Audouy JN, Berthet L et al. (2015) Hydrology under change: An evaluation protocol to investigate how hydrological models deal with changing catchments. Hydrological Sciences Journal 6667: 1–16.
- Ritter A, Munoz-Carpena R (2013) Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J Hydrol 480: 33–45.
- Moriasi DN, Gitau MW, Daggupati P (2015) Hydrologic and water quality models: Performance measures and evaluation criteria. T ASABE 58: 1763–1785.
- Dubus IG, Brown CD (2002) Sensitivity and first-step uncertainty analyses for the preferential flow model MACRO. J Environ Qual 31: 227.
- Jaber FH, Shukla S (2012) Mike She: Model use, calibration, and validation. T Asabe 55: 1479-1489.
- Feyen L, Vázquez R, Christiaens K, Sels O, Feyen J (2000) Application of a distributed physically-based hydrological model to a medium size catchment. Hydrol Earth Syst Sci 4: 47-63.
- Bruijnzeel LA (2004) Hydrological functions of tropical forests: Not seeing the soil for the trees? Agric Ecosyst Environ 104: 185-228.
- Yilmaz KK, Gupta H V, Wagener T (2008) A process-based diagnostic approach to model evaluation: Application to the NWS distributed hydrologic model. Water Resour Res 44: 1-18.
- Christina M, Nouvellon Y, Laclau JP, Stape JL, Bouillet JP et al. (2016) Importance of deep water uptake in tropical eucalypt forest. Funct Ecol In press: 1-11.
- Liu J, Luo M, Liu T, Bao A, de Maeyer P et al. (2017) Local climate change and the impacts on hydrological processes in an arid alpine catchment in Karakoram. Water (Switzerland) 9: 1-17.
- Doummar J, Sauter M, Geyer T (2012) Simulation of flow processes in a large scale karst system with an integrated catchment model (Mike She): Identification of relevant parameters influencing spring discharge. J Hydrol 426-427: 112-123.
- Sultana Z, Coulibaly P (2011) Distributed modelling of future changes in hydrological processes of Spencer Creek watershed. Hydrol Process 25: 1254-1270.
- Lørup JK, Styczen M (1990) Soil erosion modelling. In: Abbott M, Refsgaard JC (eds)Distrib. Hydrol. Model. Springer, Dordrecht. pp: 93-120.
- Pires Fernandes R, Willians da Costa Silva R, Felippe Salemi L, Morgan Berteli de Andrade T, Marcos de Moraes J et al. (2017) The influence of sugarcane crop development on rainfall interception losses. J Hydrol 551: 532-539.
- Silva RW da C, Salemi LF, Fernandes RP, de Andrade TMB, de Moraes JM et al. (2016) Throughfall patterns in sugarcane and riparian forest: understanding the effect of sugarcane age and land use conversion. Hydrol Process 30: 2579-2589.
- Xevi E, Christiaens K, Espino A, Sewnandan W, Mallants D et al. (1997) Calibration, validation and sensitivity analysis of the MIKE-SHE model using the neuenkirchen catchment as case study. Water Resour Manag 11: 219-242.
- Boyle DP, Gupta H V., Sorooshian S (2000) Toward improved calibration of hydrologic models: Combining the strengths of manual and automatic methods. Water Resour Res 36: 3663-3674.
- Madsen H, Jacobsen T (2001) Automatic calibration of the MIKE SHE integrated hydrological modelling system. In: 4th DHI Softw. Conf. Helsingør, Denmark. pp: 6-8.
- Andersen J, Refsgaard JC, Jensen KH (2001) Distributed hydrological modelling of the senegal river basin - model construction and validation. J Hydrol 247: 200-214.
- Butts MB, Payne JT, Kristensen M, Madsen H (2004) An evaluation of the impact of model structure on hydrological modelling uncertainty for streamflow simulation. J Hydrol 298: 242-266.
- Strauch AM, MacKenzie R a., Giardina CP, Bruland GL (2015) Climate driven changes to rainfall and streamflow patterns in a model tropical island hydrological system. J Hydrol 523: 160-169.
- Lane PNJ, Feikema PM, Sherwin CB, Peel MC, Freebairn AC (2010) Modelling the long term water yield impact of wildfire and other forest disturbance in Eucalypt forests. Environ Model Softw 25: 467-478.
- Dai Z, Li C, Trettin C, Sun G, Amatya D et al. (2010) Bi-criteria evaluation of the MIKE SHE model for a forested watershed on the South Carolina coastal plain. Hydrol Earth Syst Sci 14: 1033-1046.
- Lu J, Sun G, Amatya DM, Harder SV, McNulty SG (2006) Understanding the hydrologic response of a coastal plain watershed to forest management and climate change in South Carolina, U.S.A. In: Williams T (ed) Hydrol. Manag. For. Wetl. Proc. Int. Conf. St. Joseph, MI, American Society of Agricultural and Biological Engineers. pp: 231-239.
- Lørup JK, Refsgaard JC, Mazvimavi D (1998) Assessing the effect of land use change on catchment runoff by combined use of statistical tests and hydrological modelling: Case studies from Zimbabwe. J Hydrol 205: 147-163.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi