Research Article, J Nucl Ene Sci Power Generat Technol Vol: 11 Issue: 1
An Efficient Design of FSM Based 32-Bit Unsigned Pipelined Multiplier Using Verilog HDL
Prasanna Mishra*, V. M. Murugesan, G. Anand Raj
Department of Automobile Engineering, PSG College of Technology, Coimbatore,Tamil Nadu, India
*Corresponding Author: Prasanna Mishra
Department of Automobile Engineering, PSG College of Technology, Coimbatore, Tamil Nadu, India,
Tel: 9490303888;
E-mail: prasannamishra234@gmail.com
Received date: 29 December, 2021, Manuscript No. JNPGT-21-45675;
Editor assigned date: 31 December, 2021, PreQC No. JNPGT-21-45675(PQ);
Reviewed date: 14 January, 2022, QC No. JNPGT-21-45675;
Revised date: 21 January, 2022, Manuscript No. JNPGT-21-45675(R);
Published date: 24 January, 2022, DOI: 10.4172/2325-9809.1000253
Citation: Mishra P, Murugesan VM, Raj GA (2021) Design and Analysis of Suspension Test Rig. J Nucl Ene Sci Power Generat Technol 11:1.
Abstract
This paper shows a modification to FSM based 32-bit pipelined multiplier. It uses Carry Look Ahead Adders (CLA’s) and Carry Select Adders (CSA) in place of Ripple Carry Adders (RCA’s) in 32-bi t FSM based pipelined multiplier for reducing the carry propagation delay. The proposed hardware design is based on shift and add algorithm for multiplication process. Our suggested pipelined multiplier design has reduced adder and added the partial product sequentially to increase maximum operating frequency and reduce hardware resources. Synthesis report shows that modified FSM based 32-bit pipelined multiplier has less delay, less usage of logical resources, than FSM based pipelined multiplier. Simulation was done in Xilinx Vivado 2017.4(Verilog HDL).
The proposed design instantiates carry select adder for the partial product addition process, carry select adder is faster than ripple carry adder. The tradeoff between delay and power, Delay has been reduced and power increased when compared to the existing method. The proposed method can be used for the high-speed pipelined multiplication operation.
Keywords: Carry Look Ahead Adders (CLA); Ripple Carry Adders (RCA); Carry Select Adder (CSA) Finite State Machine (FSM); Partial product generators and shifters
Introduction
Multiplier circuit is a building block in digital design such as Digital Signal Processing, Microprocessors, Multiply Accumulator block, Arithmetic Logic Unit blocks, etc. Main Challenge in designing multiplier block is computation process, i.e., how efficient the multiplication process has been completed. There should be minimum computation time for multiplication. This is the reason for repeated addition method has been more preferred than multiplier blocks. There are n number of digital logic multipliers available, important factor to be considered in the multiplier logic is the computation time and time complexity. The Computation time in the logic circuit design is the amount of time required to complete the entire process in the design. When compared to adder, multiplier has more computational time and complexity. The multiplication techniques mainly involve the computing set of partial products, then summing of the partial products. The partial products are defined as the output formed by multiplying the multiplicand with each bit of the multiplier. There are mainly two types of multiplier implementation, they are combinational implementation method and pipelined implementation method [1].
In the combinational multiplier, the multiplication process is by multiplying the multiplicand against the multiplier. There are various types of multiplier logic design, in which combinational multiplier is one of the types. The other multiplier types are Array multiplier, sequential multiplier, Wallace tree multiplier, logarithm multiplier, booth multiplier, modified booth multiplier. Array multiplier, is for multiplying the two binary numbers by using an array of full adders and half adders, to form the various product, an array of AND gates is used before the adder array design. Sequential multiplier, is an outdated method in the multiplication of two binary numbers, but its relevant in many architectural designs. The below figure represents the 4-bit sequential multiplier with a3, a2, a1, a0 and b3, b2, b1, b0 are the inputs and s7, s6, s5, s4, s3, s2, s1, s0 are the outputs.
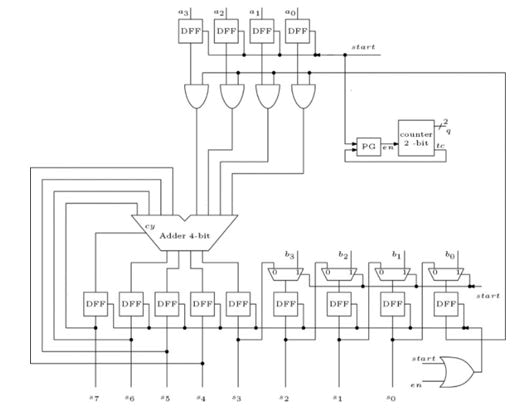
Figure 1: 4-bit Sequential multiplier.
Wallace tree multiplier is the variant of long multiplication. The Wallace tree multiplier steps are as follows, the first step is to multiply the bit of a factor by the other digit, the obtained partial products have equal weight to the product of its factors. The final product value is calculated by summing up the resultant net partial products. In this paper, we have proposed a new model approach for an efficient design of 16-bit unsigned multiplier using pipelined stages. The pipelined mechanism involves storing and executing the instruction in a sequential process. The pipeline mechanism is divided into different stages based on the architecture. The main stages of pipelining involve Fetch, Decode, Execute, Memory access and Writeback. In the proposed method, the partial product is stored in the pipelined registers in the different stages of the partial product addition. For example, for 4 row partial product block at the end of 2nd row set of pipelined registers are employed to complete the partial product addition [2].
The result supersedes the previous combinational multiplier design approach in clock cycle and operating frequency. The method used in the proposed design is repeated shift and addition operations for the partial product and the adder used in the design is Carry Select Adder for the further reduction in the delay in the carry propagation part of the instantiated adder design. To control the Finite State Machine (FSM) model, we have used mux and demux in the design.
Literature Review
Literature review discuses about different methods in designing adders and multipliers and their design comparison. The design comparison between 32 Carry look ahead adder (CLAA) bit unsigned integer multiplier and 32 bit Carry Select Adder unsigned integer multiplier were discussed. The Carry Look Ahead Adder produces carry in a faster way due to the parallel generation of the circuitry. The calculation of the carry signal propagation due to the input signal is the main reason for the circuit to be faster. In Carry Select Adder both the sum and carry bits propagated were calculated in the alternative way, Cin=0 and Cin=1, instead of waiting for Cin to propagate the Sum is computated thus by avoiding the waiting time for carry propagation, thus by greatly improving the speed. The parallel addition for the partial product and the implementation in the multiplier design were discussed the micro architecture and pipeline-based multiplier design were discussed in the paper also clarifies the pipeline stages of signed and unsigned multiply instructions. The proposed method in the paper also explains about the reduction in the count of partial products from 17 to 16, thus reducing the area of the design up to 11.6%, CISC microarchitecture used in the paper [3].
The usage of Carry Select Adder reduces the delay in the propagation in the Vedic multiplier circuit, this were discussed. The CSA is known to be one of the fastest adder, thus the Vedic multiplier is implemented using the Carry Select Adder. The results of Carry Select Adder are compared with the conventional Carry Select Adder and the modified Carry Select Adder. The main aim is to reduce the number of gates involved in the design. A novel approach to design the signed and unsigned multiplication were proposed using simple sign control unit with help of multiplexers were discussed in the method demonstrated in 0.18μm technology and the result shows reduction in silicon area overhead up to 0.45%. In addition to that, modified booth encoding techniques were employed to reduce the number of partial products in the multiplication process. Various techniques on implementing 32-bit unsigned multiplier based on pipelined architecture and combinational architecture can be found in the literature. A 32-bit unsigned multiplier is implemented in FPGA using Vedic algorithm and maximum combinational path delay achieved was 22.829 ns. Pipelined multiplier
Existing Method
The existing multiplier design is based on the FSM hardware architecture with partial product generator block, Datapath register block and FSM module. The existing architecture uses Ripple Carry Adder for the partial product addition process. The FSM block that controls the datapath module addition, mux and demux operation for the partial product. The outputs of the partial product blocks are the inputs for the datapath block, the datapath block consists of the Ripple Carry Adder and the mux, demux operation. The first stage of the block having 32 36 bit partial product and 16 bit addition, thus it needs 4 clock cycles to complete the 16 addition operation, these addition data stored in the register. Similarly, there are 16 36-bit partial products needs 8 36-bit additions. So it needs 2 clock cycles to complete these 8 additions. (P1_to_4, P5_to_8, P9_to_12, P13_to_16, P17_to_20, P21_to_24, P25_to_28, and P29_to_32) are modified into 40-bit partial product (P1_to_4 m, P5_to_8 m, P9_to_12 m, P13_to_16 m, P17_to_20m, P21_to_24 m, P25_to_28 m, and P29_to_32 m), first 36 bits assigned in the first block of the adder and then remaining 28 bits are assigned to the second block of the adder [4].
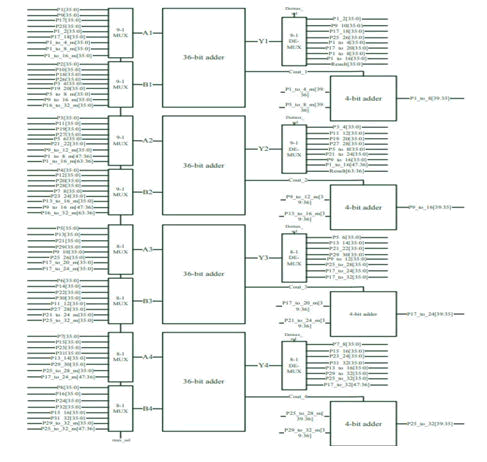
Figure 2: Datapath block.
The complete datapath block is shown in the above Figure 2. The FSM logic having the mux and demux (sel input) for the datapath block. The present state logic having the register and the next state logic having the combinational block (adder circuit).
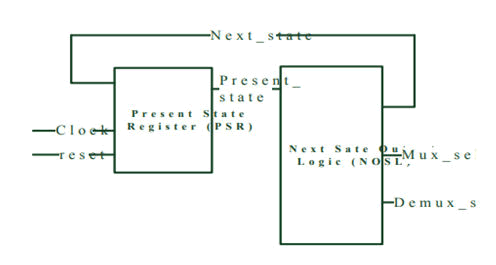
Figure 3: Finite state machine block.
Proposed Hardware Design Methodology
Design method
In this paper, we have applied repeated shift and add operation for the multiplication process. In general, n-bit multiplicand and n-bit multiplier will generate 2n-bit product. The generated n number of partial products are left shifted to one bit and added the partial product [5].
Design approach example
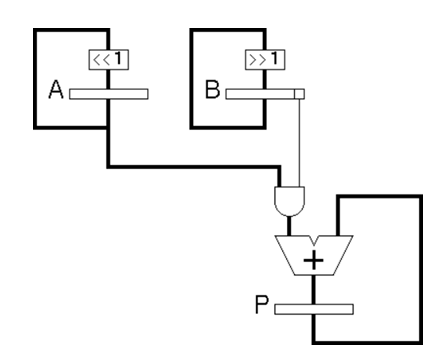
Figure 4: Shift and add multiplication block.
The figure 4 illustrates the example of shift and add operation in the design, the inputs are A and B, output Product P. Bit select operation in the least significant bit (LSB) of input B, i.e., B[0] has been taken and performed AND operation with the input A vector. In the first cycle A is added to P if the least significant bit of B is '1'. A is shifted left while B is shifted right. The process is repeated in subsequent cycles and completes when the right shifted B register has become zero (B=0). Figure 5 illustrates the multiplication process having the partial product addition method, 4-bit multiplicand and 4-bit multiplier results in 8-bit product with 4-bit partial product outputs.
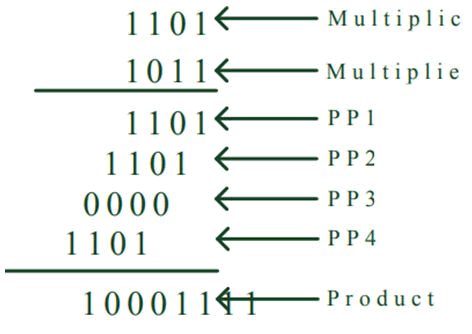
Figure 5: Multiplication example.
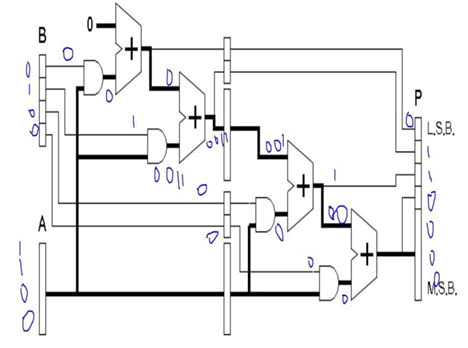
Figure 6: Pipelined multiplication.
The figure 6 shows the stages in the pipelined multiplication process. The first stage consists of set of registers with Adder, AND gate block. The LSB and the immediate next bit of the LSB of the multiplier was taken and performed the AND operation with the multiplicand, the results of the above operation stored in the register. The output of the register taken as the input for the next stage of the pipelined multiplication.
Adder comparison
The existing approach uses Ripple Carry Adder for the addition of the partial product. The carry generated in each adder gets propagated to the next adder and the carry gets sum up. Thus, the carry should propagate through the cascaded full adder stages. These encounters delay in the addition process. For 32-bit addition, the instantiated addition process takes time for the computation. Thus, the overall addition process takes delay in the computation.
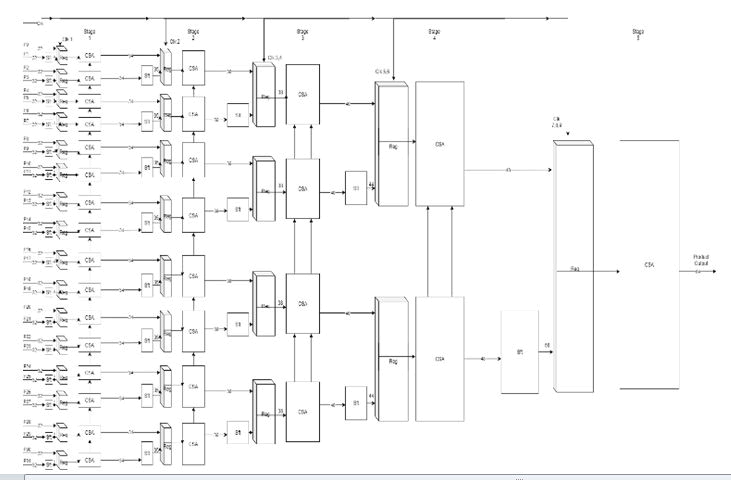
Figure 7: Proposed design block diagram.
The proposed approach suggests the usage of Carry Select Adder in the addition process for the partial product block. The instantiation of the Carry Select Adder in the place of Ripple Carry Adder may reduce the encountered delay in the addition.
Implementation of the Design
The proposed pipelined multiplier design has carry select adder instantiated for the partial product addition, the delay in the computation time for the addition process would be reduced with the help of carry select adder when compared to the ripple carry adder method.
Carry save adder design
A type of Digital adder to efficiently compute the sum of two or more binary numbers. These adders can outperform the computation operation in the multiplication. Instead of using the entire ripple carry adder instantiation in the whole partial product addition process, the carry save adder can be employed to perform the higher bit addition process. The carry save consists of n-full adders, each computes a single sum and carry bit on corresponding bits of three input numbers. The numbers are a, b and c, it produces a partial sum ps and a shift carry sc. The entire sum of the operation can be calculated by the following process. First, Shifting the carry sequence sc left by one place. Second, appending a 0 to the front of the partial sum sequence ps. Third, using a full adder to add these two together and produce the result (n+1) bit value [6].
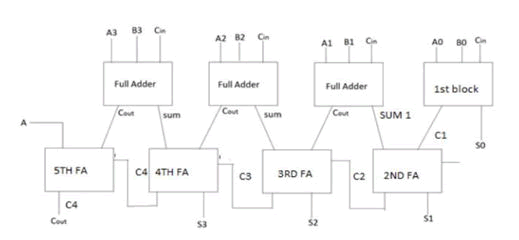
Figure 8: 4-bit carry save adder.
The above Figure shows the instantiated 4-bit Carry Save Adder for the partial product addition computation. The delay response was compared with the corresponding Ripple Carry adder and the Carry Select Adder designs.
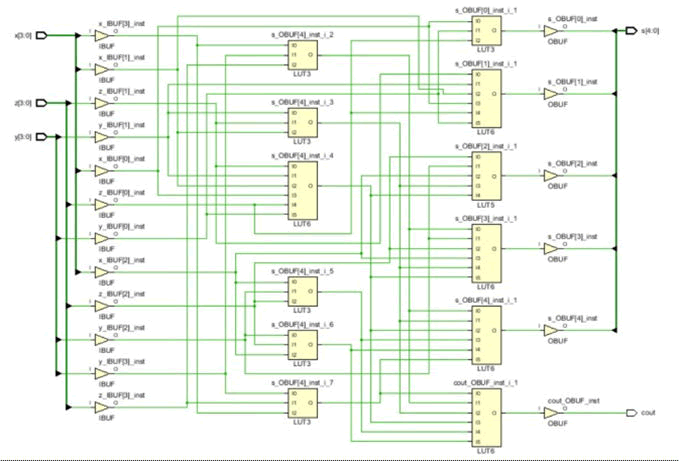
Figure 9: Synthesized schematic design of carry save adder.
Carry select adder
Carry Select Adder is an arithmetic combinational logic unit which sums up two N bit binary sum and 1 bit carry, the main difference in the Carry Select Adder and Ripple Carry Adder is the delay in the propagation of the carry. The Ripple Carry Adder will have longer delay in the carry propagation than the Carry Select Adder.
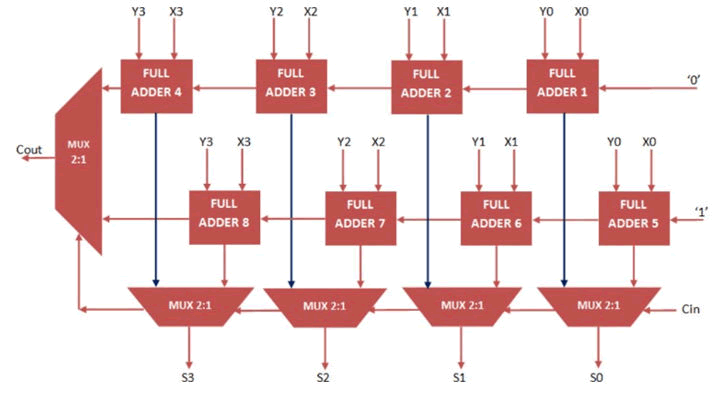
Figure 10: 4-bit carry select adder.
The above figure represents the instantiated 4-bit Carry Select Adder. At the fourth stage of the adder, the propagated carry Cout was taken out and provided as an input to the next stage of the Carry Select Adder.
Pipelined FSM multiplier design
The Proposed pipelined multiplier design with fixed latency FSM, the instantiated adder (Carry Select Adder) in the design based on the delay comparison. The FSM Block controls the Mux and Demux of the Partial product generator blocks.
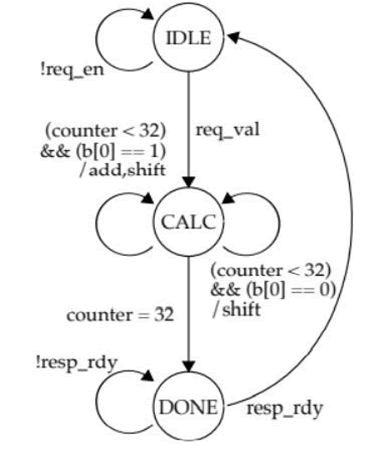
Figure 11: FSM for fixed latency.
The above figure represents the state changes for the FSM (fixed latency), the FSM has a counter to check the repeated shift and add operation. The resp_rdy signal controls the mux select lines. The counter value resets and goes back to the idle state when it reaches 32. The counter remains in Calc state (when counter less than 32) where the multiplication process is done.
Simulation Result
The schematic design of the proposed pipelined multiplier was simulated in the Vivado 2017.4. The proposed multiplier having similar five stages of the existing multiplier, the instantiated adder for the partial product addition is Carry Select Adder (due to less delay in the propagation of the carry).
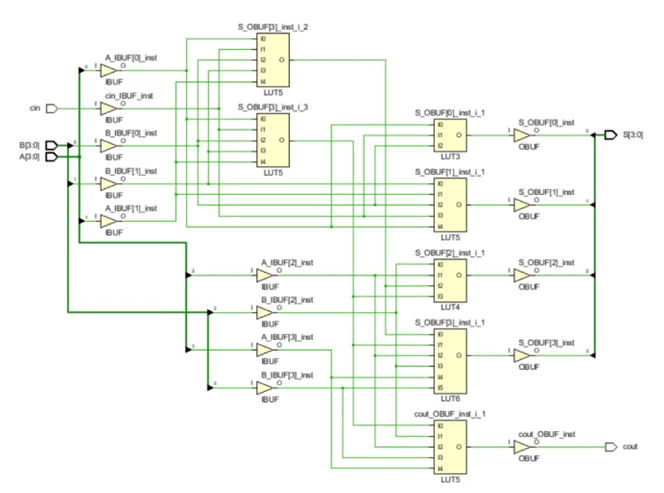
Figure 12:Synthesized schematic design of carry select adder.
The following report shows the delay comparison report of Ripple Carry Adder, Carry Save Adder and Carry Select Adder. The minimum accountable delay should be considered for the design of pipelined multiplier.
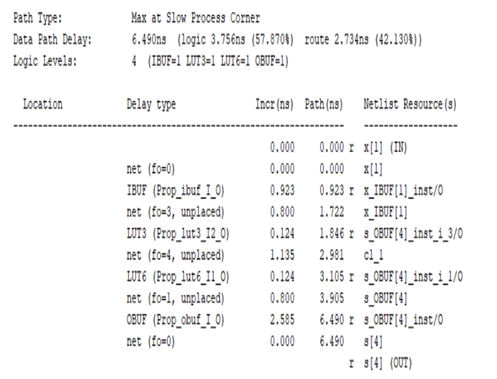
Figure 13:Timing summary of ripple carry adder.
The overall critical path delay for the ripple carry adder design is 6.49 ns. The reason for the delay is the propagation of the carry in each and every adder stages.
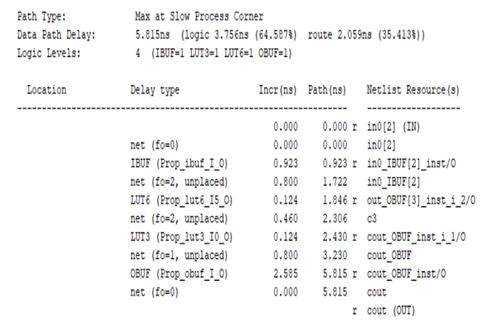
Figure 14:Timing summary of carry select adder.
The above timing summary shows the path delay for Carry Select Adder is 5.815 ns. The delay summary report of the Carry Save Adder design.
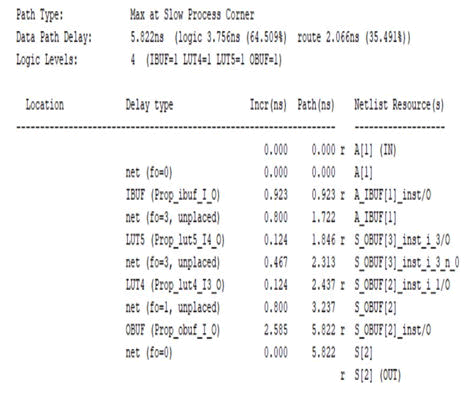
Figure 15:Timing summary of carry save adder.
The above timing summary shows the path delay for Carry Save Adder is 5.822 ns. There is a small difference in the delay between Carry Save Adder (5.822 ns) and Carry Select Adder (5.815 ns).
Figure 16: Schematic design of the proposed pipelined multiplier.
The delay reports were compared and thus the Carry Select Adder were instantiated in the Pipelined Multiplier design.
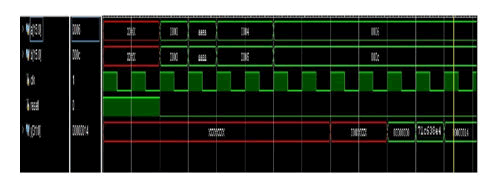
Figure 17: Simulation waveform of pipelined multiplier.
The above figure represents the simulated waveform of the pipelined multiplier, Inputs in Decimal (a-23, b-10, output of the multiplier at 9th cycle-230 in decimal). Timing Constraints include Critical path delay (the maximum delay in the reg-to-reg datapath).

Figure 18: Timing report of proposed multiplier.
The above figure shows the timing summary report of the proposed pipelined multiplier, the overall critical path delay for the multiplier is 4.01 ns (Instantiated Carry Select Adder).
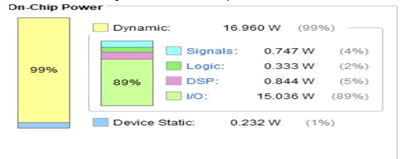
Figure 19: Power summary report of proposed pipelined multiplier.
Observation
From the above Delay comparison table, we can observe that by using Ripple Carry Adder instantiation in the design produces a delay of 7.01 ns, whereas Carry Select Adder produces a delay of 4.01 ns, clearly states that by using Carry Select Adder we can optimize the delay and improve the speed and performance of the design [7]. RCA Pipelined multiplier calculation: The inverse of the Critical path delay (max delay) gives the operating max frequency [8].
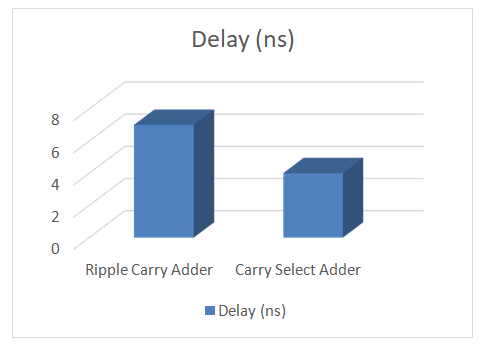
Figure 20: Delay comparison table for ripple carry adder, carry select adder, carry save adder.
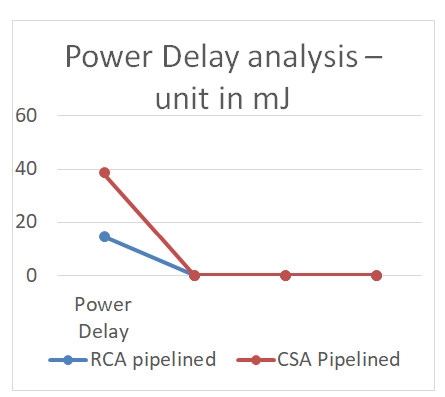
Figure 21: Power delay analysis between RCA and CSA pipelined multiplier.
The speed of the pipelined multiplier can be improved by instantiating Carry Select Adder than Ripple Carry Adder in the partial product addition process. The Power consumption of the overall Pipelined multiplier using Ripple Carry Adder (104 m W), Carry Select Adder (232 mW) [8]. We can clearly observe that there is a tradeoff between Speed and Power (i.e., Delay-Power Tradeoff in the design).
Conclusion
In the presented paper, we have designed 32- bit pipelined multiplier using Carry Select Adder, the main advantage of the Carry Select Adder instantiation is to improve the speed of the partial product addition process. The Carry Select Adder is faster than Ripple Carry Adder instantiation. The overall critical path delay for the proposed design is reduced by 17.21% than the existing path delay. The throughput has been increased by 21.02% than the existing throughput he latency and the clock cycle for the computation of the multiplication process is 9 cycles with 326 MHz frequency. The tradeoff in the proposed design is between Power and Delay. We can go for the proposed pipelined multiplier for high- speed application without the consideration of power usage.
References
- Arif S, Lal RK (2015) Design and performance analysis of various adder and multiplier circuits using VHDL. Int J Appl Eng Res 10: 17016-17020.
- Gowthami M, Jalall K, Kiruthika K (2021) High speed and performance analysis of multiplier in field programming gate array. IOP Conference Series: Mater Sci Eng 1084: 012062.
- McCanny JV, McWhirter JG (1982) Completely iterative, pipelined multiplier array suitable for VLSI. IEE Proceed G-Electr Circuit Syst 129: 40-46.
- Yan M, De-li W (2010) The design of an architecture-aware 32-bit signed/unsigned multiplier. Int Confer Compu Eng Technol 7: V7-354.
- Pekmestzi KZ, Kalivas P, Moshopoulos N (2001) Long unsigned number systolic serial multipliers and squarers. IEEE Transact Circuits Syst II: Analog Digital Signal Process 48: 316-321.
- Di J, Yuan JS, Demara R (2006) Improving power-awareness of pipelined array multipliers using two-dimensional pipeline gating and its application on FIR design. Integration 39: 90-112.
- Mounica Y, Kumar KN, Veeramachaneni S (2021) Energy efficient signed and unsigned radix 16 booth multiplier design. Comput Electric Eng 90: 106892.
- Antelo E, Montuschi P, Nannarelli A (2016) Improved 64-bit radix-16 booth multiplier based on partial product array height reduction. IEEE Transact Circuits Syst I: Regular Papers 64: 409-418.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi