Short Communication, Res Rep Math Vol: 4 Issue: 1

Bounded Energy on Compressible Fluid Dynamics and Plasma Physics with Air/Gas Flow

Tim Tarver^*

Department of Mathematics, Bethune-Cookman University, USA

*Corresponding Author : Tim Tarver
Professor, Department of Mathematics, Bethune-Cookman University, USA
Tel: +386-481-2000
E-mail: ttarver31@gmail.com

Received: March 27, 2018 Accepted: August 04, 2018 Published: October 11, 2018

Citation: Tarver T (2018) Bounded Energy on Compressible Fluid Dynamics and Plasma Physics with Air/Gas Flow. Res Rep Math 2:3.

Abstract

Keywords: Velocity vector; Partial Integratio; Exponentials

Introduction

There are problems in the field of fluid dynamics displaying difficulty to analyze fluid flow. Scientists are in the process of conceptualizing fluid flow beginning with streamlines. The goal was to generate new concepts creating some defined velocity vector 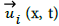and associated pressure p(x, t). According to McDonough et al. [1], a streamline is defined as a continuous line within fluids where the tangent plane at each point is the direction of some velocity vector at that point. The kicker is a velocity vector on a fluid was unknown for some time until just recently.

Body

These new ideas can possibly be used in the field of Computational Fluid Dynamics to analyze flow. The word turbulent implies unsteady fluid flow with respect to time. Contrarily, steady flow without time. The new definitions can be applied to hydrodynamics; the study of liquid flow. The flow of gases is said to have favoring characteristics as fluid flow with existing differences. If the density is unchangeable through a fluid flow field, then the fluid is incompressible. If the density of fluid flow does change, it is compressible [2]. The difference between fluids and gas come in on the natural forces being applied to liquids instead of gases.

Air, gas and fluid flow can be laminar or turbulent [3]. Laminar flow is defined as a smooth, motion of fluid where there exist deviations caused by some force [4]. The definition implies a smooth, divergence free velocity vector field 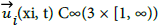with applied pressure over a streamline of liquid. Recall and note C∞ to be the set of infinite partial derivatives 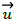with respect to x ∈ 3, showing the fluid’s incompressibility and existing bounded energy, ∀t>0.

Bounded energy

Let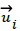 (x, t) be equal to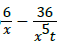

Then, we should find its bounded energy by finding the absolute value of vector 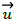squared. For example, let the velocity begin at point A (1,2). We want to determine the bounded energy of the velocity vector after it stops at point B (4,6). Next, we take the absolute value of the given vector squared to calculate the bounded energy on 3. Thus, by partial integration with exponentials we obtain

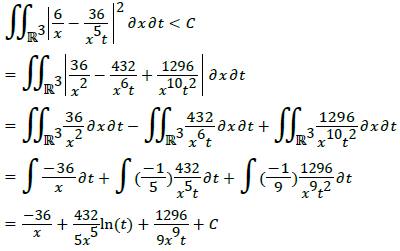
For all t strictly greater than 0 and is a subset in the differentiability class, C∞.

Streamline displacement velocity

The bounded energy can be calculated as streamline displacement velocity from point A to B. The calculations of this concept are as follows,

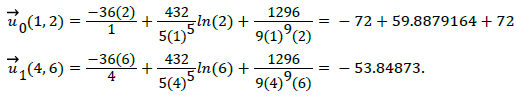
Conclusion

Thus, the displacement velocity of the given streamline vector is

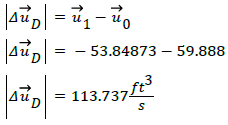
References

1. McDonough JM (2009) Lectures in Elementary Fluid Dynamics: Physics, Mathematics and Applications. University of Kentucky, Kentucky, USA.
2. Balachandran P (2006) Fundamentals of Compressible Fluid Dynamics. PHI Learning, Delhi, India.
3. Lucas J (2014) What is Fluid Dynamics? Live Science, Purch Group, Utah, USA.
4. McMurtry P (2000) Observations About Turbulent Flows. University of Utah, Utah, USA.