Research Article, J Fashion Technol Textile Eng Vol: 3 Issue: 2
Determining the Optimum Size Combination of Three-Layered Cold Protective Clothing in Varying Wind Conditions and Walking Speeds: Thermal Manikin and 3D Body Scanner Study
| Kirsi Jussila1*, Marjukka Kekäläinen2, Leena Simonen2, Helena Mäkinen1 | |
| 1Finnish Institute of Occupational Health, Aapistie 1, FI-90220 Oulu, Finland | |
| 2Centria University of Applied Sciences, Talonpojankatu 2, FI-67100 Kokkola, Finland | |
| Corresponding author : Kirsi Jussila Finnish Institute of Occupational Health, Aapistie 1, FI-90220 Oulu, Finland Tel: +358 30 474 6089 E-mail: kirsi.jussila@ttl.fi |
|
| Received: April 1, 2014 Accepted: February 23, 2015 Published: February 27, 2015 | |
| Citation: Kirsi J, Kekäläinen M, Simonen L, Mäkinen H (2015) Determining the Optimum Size Combination of Three-Layered Cold Protective Clothing in Varying Wind Conditions and Walking Speeds - Thermal Manikin and 3D Body Scanner Study. J Fashion Technol Textile Eng 3:2. doi:10.4172/2329-9568.1000120 |
Abstract
Garment fit and still air between clothing layers affect heat transfer through the clothing and thus the thermal insulation. Wind and body movement decreases clothing insulation by causing ventilation inside the clothing and by compressing air layers. The objective was to find the optimum size combination of three-layered clothing at two different wind speeds, and in stationary and walking situations, and to evaluate the effect of the wind direction on thermal insulation and air gaps inside the clothing. The clothing ensembles consisted of three layers (base, mid, outermost layer) in twelve different size combinations. The thermal insulation of the ensembles were measured in a climatic chamber (ambient temperature 10 °C, wind speed 0.3 m/s and 8 m/s) using both a static and moving thermal manikin. Whole body and cross-sectional figures of each clothing layer were taken by a 3D body scanner. The results showed that in calm conditions, static total thermal insulation was higher when the mid- and outermost layers were larger in size. When air movement was added by wind and body movement, thermal insulation reached its highest value when the outermost layer was one size larger than recommended in EN 13402-3.
Keywords: Cold protective clothing; Clothing size; Thermal manikin; 3D body scanning; Cold; Wind
Keywords |
|
| Cold protective clothing; Clothing size; Thermal manikin; 3D body scanning; Cold; Wind | |
Abbreviations |
|
| AG = thickness of the air layer | |
| Ia = thermal insulation of the boundary air layer measured with a stationary thermal manikin | |
| Iar = thermal insulation of the boundary air layer measured with a moving thermal manikin | |
| Icle = effective thermal insulation from skin to outer clothing surface measured with a stationary thermal manikin | |
| Icler = resultant effective thermal insulation from skin to outer clothing surface measured with a moving thermal manikin | |
| It = total thermal insulation from skin to ambient measured with a stationary thermal manikin | |
| Itr = total resultant thermal insulation from skin to ambient measured with a moving thermal manikin | |
| SD = standard deviation | |
Introduction |
|
| In cold conditions, the thermal insulation of clothing must be adequate for sustaining body heat balance. If both ambient temperature and physical activity are low, the required thermal insulation is so high that a multi-layered clothing system is needed. It is well known that garment fit and still air between clothing layers and in textiles affect heat transfer through the clothing and thus also affect thermal insulation [1-4]. In a previous study using one clothing layer on the torso, the thermal insulation value increased with a thicker air layer entrapped between the clothing and skin, but the value started to drop if being higher than the optimum air layer thickness [1]. Another study determined the maximum thermal insulation value of twolayered clothing on the torso in relation to air volume between the garment layers [3]. | |
| In real conditions, air between clothing layers does not form uniform layers, but air gaps are formed. Air gaps inside clothing are not evenly distributed over the body and the number of small air gaps is greater than of large ones [5]. It has been found that in tight-fitting clothing, air gap thickness was almost constant for all body parts, whereas in loose-fitting clothing the air gap thickness was typically about 40% larger, and the largest differences were distributed around the sections of abdomen, lower back, lumbus and anterior and posterior pelvis [6]. | |
| Several environmental and user-related factors are known to influence the thermal insulation of cold protective clothing. Wind increases convective heat loss and compresses air content inside the clothing, which decreases thermal insulation [2,7-9]. It is also known that body movement causes a ‘pumping effect’, which increases air movement and ventilation inside the clothing, and thus heat transfer from the clothing increases and clothing insulation is reduced [2,8,10,11]. As regards the interaction effects of body movements and wind on thermal insulation, it has been reported that the higher the wind speed, the smaller the effect of movement, such as walking [8,12]. In addition, the ‘pumping effect’ was found to be greater when clothing permeability was lower [8]. When evaluating the insulation properties of clothing, the effects of wind speed and human movement can be taken into account by correcting for static insulation values [8,10]. Clarification is needed of these effects on the clothing thermal insulation of different clothing sizes. Based on the scientific literature, it is still not properly known how wind direction towards the body affects the thermal insulation of cold protective clothing. | |
| Air content in clothing can be measured by pinching the fabric from different points of the body or by calculating the difference between the clothing measures and manikin or test subject [1, 13]. Recently, 3D body scanning methodology has been used to analyse garment fit and air gaps inside clothing. This method has also been used in several studies to evaluate air layers in flame protective clothing and their relation to thermal insulation and burn injuries [5,14,15]. The 3D scanning method has proven to give comparable results with manual measurements and is a valuable tool for objective ratings and the fit evaluation of garments [3,5,6,16-19]. | |
| The aim of this study was to find the optimum size combination of three-layered, cold protective clothing through measurements using a thermal manikin and 3D body scanner in a climate chamber. The purpose was to deepen the knowledge on the effects of air content and clothing size in cold and windy conditions. In addition, we aimed to clarify the influence of wind direction against the body, and its influence on effective thermal insulation and air gap distribution inside the clothing. | |
Materials and Methods |
|
| Thermal manikin and clothing ensembles | |
| An aluminum thermal manikin (Finnish Institute of Occupational Health, Helsinki, Finland) consisting of twenty segments was used in the measurements. It has the size of male person with a height of 176 cm, chest circumference of 96 cm, waist 88 cm, hip 96.5 cm, thigh 55 cm, calf 37 cm, and 1.89 m² body surface area. According to the body measures, the body type of the thermal manikin was ‘normal’ (C), the height group was 176 ± 3 cm, and the clothing size was M or between sizes 48 and 50, based on girth measures of the chest and waist [20,21]. | |
| The measured clothing ensembles included three layers (base, midand outermost). The outermost layer was two-piece clothing in four sizes (48, 50, 52, 56), the mid-layer was in three sizes (XS, M, XL), and the base layer was size S in all cases (Figure 1). | |
| Figure 1: The three measured clothing layers in different sizes and nude thermal manikin from upper left: nude thermal manikin and base layer (size S); middle left: mid-layer sizes XS, M, L; lower left: outermost layer sizes 48, 50, 52, 56. The measurement points were marked by tape (chest, waist, hip, thigh, calf) to indicate the crosssectional evaluation points in 3D body scanning. | |
| The strap at the hem line of the outermost jacket was slightly tightened. Table 1 provides information on the clothing layer materials and table 2 shows the measured combinations of the different layer sizes. The thickness of the garments was measured in accordance with the EN ISO 5084 standard [22]. | |
| Table 1: Material information of the three clothing layers (base, midand outermost). | |
| Table 2: Sizes of different layers of measured clothing ensembles. | |
| Thermal insulation measurements | |
| The thermal insulation of the dry cold protective clothing ensembles was measured in a climate chamber (length 10.3×width 4.4×height 3.3 m) of the Finnish Institute of Occupational Health. The thermal insulation was measured according to standards EN ISO 15831 [23] and EN 342 [24], using both static and moving (walking speed 0.51 m/s, 45 double steps/min) thermal manikin. The moving thermal manikin simulates walking by moving both arms and legs during the experiment. The thermal insulation values were evaluated on whole body and locally in the separate segments of the thermal manikin. The surface temperature of the thermal manikin was set to 34.0 ± 0.1 °C [23]. Calibration of the used equipment was performed according to the standards. | |
| The ambient temperature in the climatic chamber was adjusted to 10 °C, in accordance with the used standards [23, 24]. The relative humidity in the climatic chamber was not controlled during the experiments and was measured as about 40 ± 5% on average. The EN ISO 15831 standard [23] requires the ambient temperature to be set at least 12 °C below the thermal manikin’s mean surface temperature to provide reliable results. In addition, the simultaneously used 3D body scanning equipment was sensitive to subzero temperatures. Two different wind speeds were selected to simulate low, 0.3 m/s, and high, 8.0 m/s, wind conditions. The low wind conditions were represented by intrinsic air flow in the climatic chamber and simulated calm wind conditions. The effect of the wind direction on thermal insulation, at high wind conditions (8 m/s) was measured by turning the thermal manikin to three different angles towards the wind, 0°, 45° and 90° (Figure 2). The wind (8 m/s) blowing horizontally from the front of the thermal manikin corresponded with the 0° angle, and when the thermal manikin was turned 45° and 90° to the wind, the left side of the thermal manikin was facing the wind. For practical reasons only one ensemble (C3) was chosen to determine the effect of wind direction. | |
| Figure 2: Effects of wind direction (wind speed 8 m/s) on effective thermal insulation (Icle) of clothing ensemble C3, tested at angles of 0°, 45° and 90° to the wind. | |
| The clothing insulation was evenly distributed over the body, thus the total thermal insulation (It) and the resultant total thermal insulation values consisting all garments, enclosed air layers, and boundary air layers were calculated using serial model by Formulas 1 and 2 [23]. The thermal insulation values are presented in SI units (m²K/W). | |
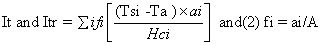 |
|
| where It is the total thermal insulation of the clothing (m²K/W), fi is the surface area factor of each manikin zone, Tsi is the average manikin temperature (°C), Ta is the air temperature (°C), ai is the surface area of the manikin zone (m²), Hci is the wattage of the manikin zone (W), and A is the total surface area of the manikin (m²). | |
| The effective thermal insulation (Icle) and the resultant effective thermal insulation (Icler) from skin to outer clothing surface of the ensembles were determined by Formulas 3 and 4: | |
| (3) Icle = It − Ia and (4) Icler = Itr − Iar | |
| where Ia is the insulation provided by the air layer around the nude static thermal manikin (m²K/W), and Iar is the insulation provided by the air layer around the nude moving thermal manikin (m²K/W). | |
| Evaluation of garment size by 3D body scanning | |
| The undressed static thermal manikin and each clothing layer in different sizes were scanned on the static thermal manikin by a 3D body scanner using Human Solutions ScanWorX: Anthroscan software. A total of 31 scanned whole body pictures were taken. Each separate 3D-scanned clothing layer and undressed thermal manikin was overlaid into one picture using the x,y,z coordinates of the software. This ensured the correct location of each scanned layer. | |
| The same dressing protocol was followed before each experiment to make sure the changes in air gaps were minimized. In all of the whole body pictures, the thermal manikin wore socks and boots. The hip of the thermal manikin was locked to give it a stable standing position. | |
| From the scanned figures, cross-sectional measurements were made at five points: the chest (distance from the ground 133 cm), the waist (113 cm), the hip (94 cm), the thigh (72 cm), and the calf (39 cm). The used software was able to estimate the areas missed during scanning, for example, under the arm and the crotch. However, these missed areas were considered as outliers. The measurement points were marked by tape to indicate the cross-sectional points on the thermal manikin and the different clothing layer surfaces (Figure 1). | |
| Air content determination | |
| To evaluate the air layer thickness inside the clothing system, the body girth of each clothing layer and the thermal manikin were measured by a 3D scanning system at five different points, as described in the previous section. The thickness of the air layer (AG) between the clothing layers was calculated using Formula 5 [1]: | |
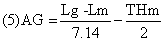 |
|
| where AG is the thickness of the air layer (cm), Lg is the body girth of the upper garment (cm), Lm is the body girth of the manikin (cm), THm is the compressed thickness of fabric (cm), and constant 7.14 is the mean value of 2π and 8, as the real cross-section of the body girth is between a circular and rectangular shape. | |
| The cross-sectional pictures of each clothing combination (C1 – C12) were pooled into one picture illustrating the layered clothing system. The thickness of the air layers between the clothing layers were also estimated at ten sites from these pooled pictures by using the Anthroscan software (Figure 3). Total average values were also calculated at the front and back and both sides. | |
| Figure 3: Effects of wind direction (wind speed 8 m/s) on effective thermal insulation (Icle) of clothing ensemble C3, tested at angles of 0°, 45° and 90° to the wind. | |
Results |
|
| Thermal insulation of different sized clothing ensembles | |
| Static thermal insulation | |
| In calm conditions (0.3 m/s) with the stationary thermal manikin, the effective thermal insulation (Icle) without the boundary air layer was used to analyse relative changes in the insulation values of the different clothing size combinations. The insulation of the surface air layer (Ia) of the nude stationary thermal manikin on clothing area in calm conditions (0.3 m/s) amounted to 0.090 mK/W (0.58 clo). The Icle varied from 0.42 to 0.54 m²K/W (2.7 – 3.5 clo) as shown in figure 4. | |
| Figure 4: Effective thermal insulation (Icle) of clothing ensembles in calm (0.3 m/s) and wind (8 m/s) with static thermal manikin. In each ‘mid-layer size’ section, 1st ensemble consists the smallest outermost clothing and 4th the largest.. | |
| The relative difference in measured values ((Icle_min – Icle_max)/ Icle_max × 100 (%)) was about 23%. The Icle was higher when the midand outermost garments were larger in size. In windy conditions (8 m/s) the boundary air layer around the ensembles broke down due to air movement. In wind the static thermal insulation of the ensembles increased when the outermost garments were larger in size, but the effect of different mid-layer sizes was not significant. The relative decrease in the static clothing thermal insulation caused by wind ((Icle_calm - It_wind)/ It_wind × 100 (%)) was on average about 15% (standard deviation (SD) ± 2.3). The relative decrease by wind was higher when the outermost clothing size was larger. | |
| Closer evaluation of the local Icle values on the torso in calm (0.3 m/s) revealed that the Icle_torso increased when the outermost garment was larger in size, and the size of the mid-layer garment did not have a remarkable influence. The Icle_torso varied from 0.34 to 0.50 m²K/W (2.5 – 3.2 clo) in calm conditions. In windy conditions, the highest static thermal insulation value on the torso was measured when the mid-layer garment size was M and the outermost garment sizes were 52 and 56. The Icle on the legs (thigh and shin) was the greatest when the outermost garment was the largest in both calm and windy conditions. The Icle_legs varied from 0.47 to 0.57 m²K/W (3.0 – 3.6 clo) in calm conditions. Figure 5 presents the relative effect of the wind on the static thermal insulation on part of upper and lower body and whole clothing area. The relative decrease by wind on Icle on the torso as well as the chest was the smallest, 21% (± 2.3) and 33% (± 2.3) respectively, when the outermost garment was a size 52. On the legs (thigh and shin), the relative decrease by the wind on Icle was the smallest, on average about 4% (± 2.3), when the outermost clothing size was the smallest. | |
| Figure 5: Relative effect (%) of wind (8 m/s) on effective thermal insulation (Icle) on different body parts and whole clothing area. In each ‘mid-layer size’ section, 1st ensemble consists the smallest outermost clothing and 4th the largest. | |
| Resultant thermal insulation | |
| The resultant effective thermal insulation (Icler) was used to analyse relative changes in the insulation values of the different clothing size combinations in calm conditions (0.3 m/s) with the moving thermal manikin (walking speed 0.51 m/s). The insulation of the surface air layer (Iar) of the nude moving thermal manikin on clothing area in calm conditions (0.3 m/s) amounted to 0.084 m²K/W (0.54 clo). The Icler of the ensembles in calm varied from 0.37 to 0.42 m²K/W (2.4 – 2.7 clo). The relative difference in measured values ((Icler_min – Icler_max)/ Icler_max × 100 (%)) was about 12%. In wind (8 m/s) the boundary air layer around the ensembles was lost. The clothing thermal insulation measured by the moving thermal manikin in both calm and windy conditions did not reveal significant differences between different mid-layer sizes. When the outermost clothing layer was larger, the clothing thermal insulation tended to be greater. A relative decrease in the resultant clothing thermal insulation caused by wind ((Icler_calm - Itr_wind)/ Itr_wind × 100 (%)) was on average about 10% (SD ± 3.5). The relative decrease of clothing thermal insulation by movement in calm conditions was on average about 17% (SD ± 3.9) and about 13% (SD ± 3.4) in the wind. The combined decrease of the clothing thermal insulation caused by walking and wind (8 m/s) was on average about 26% (SD ± 4.9). The relative decrease by wind, movement or their combination was higher when the outermost clothing size was larger. | |
| Examination of the local Icler on the torso showed that the values were at their highest when the mid-layer size is M and the outermost layer was 52 in both calm and windy conditions (Figure 6). | |
| Figure 6: Resultant effective thermal insulation (Icler) on torso measured in calm (0.3 m/s) and windy (8 m/s) conditions with moving thermal manikin. | |
| The combined effect of wind (8 m/s) and movement decreased Icler on the upper and lower body relatively the greatest when the outermost garments were the largest in size and correspondingly the least when outer garments are the smallest (Figure 7). | |
| Figure 7: Relative effect (%) of wind (8 m/s) and movement (walking) on effective thermal insulation (Icle) on different body parts and whole clothing area. In each ‘mid-layer size’ section, 1st ensemble consists the smallest outermost clothing and 4th the largest. | |
| Air content in layered clothing | |
| The girth of each clothing layer and the difference between the garments and the body at five body points were determined from the cross-sectional pictures, and the differences in the girths are presented in table 3. | |
| Table 3: Difference in girth at the waist compared to girth of unclothed thermal manikin. | |
| The thickness of the air layer (AG) between the outermost garment and the unclothed body was calculated (Formula 5) and measured from the cross-sectional figures. The measured results were about 14% higher than the calculated results (Figure 8). | |
| Figure 8: Thickness of air layer between outermost garment and unclothed thermal manikin at the waist. | |
| Relation between thermal insulation and air content | |
| The thermal insulation in windy and walking situations was highest when the mid-layer was size M. The relation between the thermal insulation on the torso and air layer thickness from the skin surface to the outermost layer at the waist is presented in figure 9. | |
| Figure 9: Effective thermal insulation (Icle) on torso with mid-layer size M in relation to air layer thickness from inner surface of outermost garment to skin at waist. | |
| The figure shows two different curve shapes, one for the static and one for the walking situations. In the static situations, including both calm and windy conditions, the measured Icle tended to be higher when the outermost garment was larger, but in windy conditions, the Icle reached its highest value and indicated no tendency to further increase. The second curve shape in figure 9 represents the walking situations in which the highest cusp of the Icler was when the distance from the inner surface of the outermost garment to the skin was 4.7 cm. The Icler was lower if the garment size was smaller or larger than at the cusp. In addition, higher Icler was seen with the smallest outer garment, when the pumping effect caused by walking was diminished due to thin air layers inside the clothing. It was resulted that when the outermost layer was a size 52 and the mid-layer was a size M the thermal insulation reached its highest value in windy and moving conditions. | |
| Effect of wind direction | |
| The effect of wind direction on the static thermal insulation of the clothing system was evaluated by turning the thermal manikin to a 0°, 45°, and 90° angle to the wind. The effect of the wind on the Icle was greatest when the body was at an angle of 0° to the wind, and smallest when the angle was 45° (Figure 10). The wind effect was the smallest when the direct contact surface with the wind was the smallest. | |
| Figure 10: Relative effect (%) of wind from different directions (0°, 45° and 90° to the body) on effective thermal insulation (Icle) of clothing system (C3). | |
| The thermal manikin was turned left side towards the wind at a 45° and 90° angle. Thus, the wind had a higher compressive and convective heat loss effect on the left side than on the right. Figure 11 shows the differences in the relative effect of the wind direction on the local Icle values of the right and the left side of the body on the upper arm, forearm, thigh and shin. The relative decrease of the local Icle by the wind from the 45° angle on the left side was on average of about 10% ( 5.2) and on the right side about 7% ( 4.5). When the thermal manikin was at a 90° angle to the wind direction, the relative decline on the left side was on average about 13% ( 11.8) and on the right side about 5% ( 9.8). | |
| Figure 11: Relative effect (%) of wind direction on local effective thermal insulation (Icle) values at right and left side on upper arm, forearm, thigh and shin. | |
| The effects of wind direction were the most visible in the air gap movements on the waist area. When the wind direction was at a 45° angle to the body, the evaluation of the air gaps from cross-sectional figures on the waist area revealed that air content had increased on the right side of the body compared to the situation in calm conditions (Figure 12). | |
| Figure 12: Cross-sectional pictures of waist when wind direction was 0° and 45° in calm (0.3 m/s) and in wind (8 m/s). | |
| Similarly, when the wind was blowing from the left side (90° to the body), the air content was compressed on the left side, and greater on the right side (Figure 13). | |
| Figure 13: Cross-sectional pictures of waist when wind direction was 0° and 90° in calm (0.3 m/s) and in wind (8 m/s). | |
Discussion |
|
| This study sought to find the optimum garment size of threelayered clothing systems in order to determine the highest possible thermal protection in cold, static, walking and windy conditions. In addition, the study examined the effects of different wind directions against the body on thermal protection in the cold. In our study we considered the optimum size of the three-layered cold protective clothing system, and therefore did not taking into account the possible effects of clothing size on the increased accident risk of garment grabbing for instance. | |
| Thermal insulation of different sized clothing ensembles | |
| In this study the effective thermal insulation (Icle) and the resultant effective thermal insulation (Icler) without the insulative boundary air layer around the ensembles were used to analyse relative changes in the intrinsic clothing insulation of the different clothing size combinations. Total thermal insulation (It) decreases greatly in windy conditions, due to the breakdown of the boundary air layer around the clothing surface. The thermal insulation of the boundary air layer (Ia) in calm condition (0.3 m/s) with the static thermal manikin was on average about 16% of the total thermal insulation and about 19% with the moving thermal manikin. The differences caused by the outermost and mid-layer clothing sizes were able to identify using effective thermal insulation without the effect of boundary air layer. | |
| It has previously been shown that tight clothing fit has 6–32% lower insulation than loose-fitting clothing in wind speeds of 0.5 − 2 m/s [1-3]. In this study, tight clothing (size 48) provided on average about 17% lower effective thermal insulation in calm conditions and 13% lower in windy conditions (8 m/s) than the loose-fitting clothing (size 56). In calm conditions, static effective thermal insulation was higher when the outermost layer was larger in size. When the outermost garment was loosely fitting, the thermal insulative air layers were thicker under the clothing system providing higher effective thermal insulation. In this study the effect of different materials and fabric constructions on thermal insulation was eliminated by using same materials in each clothing ensemble. It was seen previously that the total thermal insulation differed by about 8% between three fourlayered cold protective clothing systems developed for same purpose, but made from different conventional textile materials [25]. This suggests that clothing size may have relatively the same importance as choices of commonly used textile materials in layered clothing in evaluation of thermal insulation. | |
| In windy conditions (8 m/s) the boundary air layer around the ensembles broke down due to high air movement. In addition, the wind compressed air layers and increased ventilation inside the clothing [2,7,8,10], thus decreasing the effective thermal insulation values. When the outermost clothing was the smallest in size the relative effect of the wind was greatest on the chest, due to almost total compression of the air layers underneath the clothing system. In contrast, when the clothing size was the largest, the relative effect of the wind increased due to convective heat loss by ‘chimney effect’ [26]. Furthermore, the relative effect of the wind was smaller in the lower body parts than in the torso. This is most probably due to the higher contact surface area of the torso with the direct wind, causing a greater compressive effect on the torso than on the lower part of the body. | |
| Movement of the thermal manikin causes a ‘pumping effect’ underneath the clothing which means increased air exchange from the clothing to the ambient air. The effect then increases convective heat loss and decreases the thermal insulation of the clothing. [2, 8, 10] In previous study, it has been proposed that the effect of movement is smaller when the wind speed is higher [8, 12]. Anttonen and Hiltunen [12] found that a walking speed of 0.3−0.8 m/s decreased the total thermal insulation by about 10−20% in low wind speed (0.4 m/s) and about 5% in a wind speed of 18 m/s. The results of this study showed that the relative effect of body movement (walking speed 0.51 m/s) was on average higher in calm (17%) than in windy conditions (13%). This was seen when the two smallest outermost clothing sizes were used. Whereas, the relative effect of body movement was greater in wind with the two largest outermost garments and the effect was the highest with the largest outermost garments. Size M mid-layer provided the highest thermal insulation values in the wind and with movement. This indicates that a tight-fitting mid-layer creates a thick air layer between the mid- and outermost layers, in contrast to a loose fit between the mid- and base layers. An excessively thick air layer increases convection and the pumping effect under the clothing. | |
| Measurements in calm and windy conditions using both a static and moving thermal manikin showed that effective thermal insulation values of the ensembles tended to be higher when the outermost clothing layer was larger. The relative decrease in the effective thermal insulation by wind, movement or their combination was the lowest when the outermost clothing was the smallest and the highest when the outermost clothing was the largest. The relative decrease in the static effective thermal insulation caused by wind was on average about 15%, and by movement about 17%. The combined effect of wind and movement decreased the effective thermal insulation on average about 26%. | |
| Locally, the cusp of the effective thermal insulation of different clothing sizes was more visible. In wind and with movement, midlayer size M provided the highest effective thermal insulation values on the torso, whereas outermost clothing size 52 provided the highest values and had the smallest relative effect caused by wind on the upper body in static situations. The selected base layer size was tight-fitting in the all ensembles. The clothing size of the thermal manikin was M or between 48 and 50, based on the girth measures of the chest and waist [20, 21]. Thus the results infer that the optimum size of the midlayer is similar to those recommended in the standard and that outermost clothing size should be one size larger than recommended. | |
| The thermal manikin tests were performed in this study to be able to produce accurate and comparable results. The reproducibility of the thermal insulation test results in a single has shown to be good and the coefficient of correlation being lower than 3% [27]. The EN ISO 15831 standard [23] contains two different methods for calculating the thermal insulation of clothing ensembles; serial and parallel. Previous literature reveals that the serial method provides slightly higher thermal insulation values than the parallel method [28]. The mean relative difference between the methods in the static and resultant thermal insulation measurements [(static-resultant)/static] has been lower with the serial method than with the parallel method. The relative differences were evaluated as more significant when the distribution of the thermal insulation over the body was uneven [29]. This study only compared the thermal insulation values between the clothing ensembles, and evaluated the relative differences between the ensembles. Thus the calculation method used did not significantly affect the obtained results. | |
| Air content in layered clothing | |
| A previous study reported that thermal insulation increases linearly with the thickness of the air space until about 1.3 cm is measured between the two plates. After this, the insulation decreases due to convection caused by air movement in a wider air space [30]. A previous study showed that the highest thermal insulation value of one-layer clothing was obtained when the thickness of the air layer was 1 cm (corresponding to 7.5 cm difference in girth) in calm conditions and 0.6 cm (corresponding to 5 cm difference in girth) in wind at a speed of 2 m/s [1]. Another study proposed that with two-layered clothing, the highest thermal insulation value without a cooling effect caused by ventilation was obtained by having a distance of 2.3 cm between the body and outer garment on the chest [3]. In our study, the difference in girth was considerably higher, but this result is reasonable when taking into account that two layers of clothing were used underneath the thick outermost layer. The selected base layer size was tight-fitting in all the ensembles, and thus no space for an air layer between the body and inner layer existed. In this study, a size 52 outermost garment had about a 35 cm difference in waist girth (40% larger than body girth), and the distance from the inner surface of the outer layer was 4.7 cm. A size M mid-layer had about an 18 cm difference in waist girth (20% larger than body girth). Air layer thickness between each garment layer was calculated using Formula 5, which extracts the thickness of the fabric. This revealed that the air layer thicknesses were about 2.2 cm and 2.4 cm between the inner and mid layers, and mid and outer layers, respectively. The mid layer divided the air content inside the clothing into two halves between the inner and outer layers, when the inner layer was closely fitted to the skin. | |
| The used software for 3D body scanning, provided accurate body girth measures of the different clothing layers. The software has not been commonly used in the evaluation of air gaps and air layer thicknesses, thus the method in this study was applied in a new context. To provide reliable results regarding the air gaps and layer thicknesses between garment layers, the 3D body scanning results were combined with the calculated air layer thickness values. The method provides solution to evaluate distribution of air gaps inside the clothing and to find the problematic areas of conductive heat loss or ventilation, which gives useful information for cold protective clothing development and design. | |
| Effect of wind direction | |
| The literature contains several studies of the effect of wind on heat transfer by convection [2,7,8]. In most of the studies, the wind has blown horizontally against the front side of the body, the equivalent to the 0° wind direction in our study. This study showed that the heat transfer mechanism was different in the left and the right side of the body when position of the thermal manikin was changed towards the wind direction. The 3D pictures revealed that the wind compressed the thickness of the air layers to the minimum on the left side, and thus the effective thermal insulation was decreased. On the other hand, the air layer thickness was increased on the right side and ventilation inside the clothing due to ‘chimney effect’ occurred. The relative decrease of the effective thermal insulation was about 10% and 13% on the left side and 7% and 5% on the right by the wind from the 45° and 90° angle, respectively. The decreased effect of the wind on the effective thermal insulation appeared to be smallest when the body was turned to a 45° angle to the wind direction and greatest when the wind was blowing directly against the body (0° angle). This seemed to be related to the contact surface area of the direct wind with the body, and thus, the compressed air layer underneath the outermost garments were smallest at a 45° angle to the wind direction. | |
Conclusion |
|
| This study determined the optimum garment size of different layers of three-layered clothing for maximum thermal insulation in the cold, as well as in walking and windy conditions. The results showed that the effective thermal insulation in calm conditions was greater when the mid- and outermost layers were larger in size. When air movement by wind (8 m/s) and movement of the thermal manikin were added, the effective thermal insulation on torso reached its highest value when the mid-layer size (difference in waist girth 18 cm) was in accordance with the recommendations of European standard EN 13402-3 (2004) and the outermost clothing size was one size larger (difference in waist girth 35 cm). If the air layer between the clothing layers increased more, the thermal insulation decreased, especially due to a pumping effect caused by walking. The relative effect of the wind was smaller in the lower body parts than in the torso. Wind had the least effect on effective thermal insulation when the body was at a 45° angle against the wind direction. This suggests that the exposed contact surface to the wind and thus the compressed air layer area underneath the outermost garments were the smallest at this wind direction. | |
| The results of this study provide specific information for cold protective clothing development and design as well as manufacturers, retailers and end users on the optimum body girth looseness of layered cold protective clothing in order to obtain the highest possible thermal insulation. As a result, it is suggested that these results should be taken into account in standardization of protective clothing against cold. Future studies should investigate the optimum size of layered cold protective clothing in different body positions. | |
Acknowledgments |
|
| This research was carried out as part of project called the Protection and safety of travellers and tourism workers, which was financially supported by the European Union (European Social Fund). The authors wish to express their thanks for this support. | |
References |
|
|
|
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi