Research Article, Res Rep Math Vol: 2 Issue: 1
Existence of Solutions for Impulsive Second Order Abstract Functional Neutral Differential Equation with Nonlocal Conditions and State Dependent-Delay
Karthikeyan K1*, Sundararajan P2 and Senthil Raja D1
1Department of Mathematics, KS Rangasamy College of Technology, Tamil Nadu, India
2Department of Mathematics, Arignar Anna Government Arts College, Tamil Nadu, India
*Corresponding Author : Karthikeyan K
Department of Mathematics, K.S.Rangasamy College of Technology, Tiruchengode – 637 215, Tamil Nadu, India
Tel: (04288) 274741 to 274744
E-mail: karthi_phd2010@yahoo.co.in
Received: July 17, 2017 Accepted: January 15, 2018 Published: February 10, 2018
Citation: Karthikeyan K, Sundararajan P, Senthil Raja D (2018) Existence of Solutions for Impulsive Second Order Abstract Functional Neutral Differential Equation with Nonlocal Conditions and State Dependent-Delay. Res Rep Math 2:1
Abstract
In this paper, we study the existence of mild solutions for the impulsive second order abstract partial neutral differential equations with state dependent delay of the form
Keywords: Abstract Cauchy problem; Impulsive differential equations; Cosine function; State-dependent delay
Introduction
In this paper, we study the existence of mild solutions for the impulsive second order abstract partial neutral differential equations with state dependent delay of the form
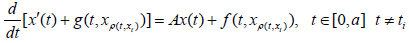 (1.1)
(1.1)
with the nonlocal conditions
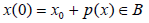 (1.2)
(1.2)
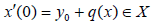 (1.3)
(1.3)
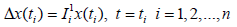 (1.4)
(1.4)
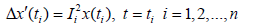 (1.5)
(1.5)
where A is the infinitesimal generator of a strongly continuous cosine function of bounded linear operator (C(t))t∈R defined on a Banach space (X,||.||), the function 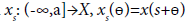 belongs to some abstract phase space B described axiomatically and
belongs to some abstract phase space B described axiomatically and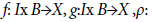
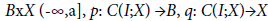 and
and
Ii, Ji: B→X, i=1,2,…,n are appropriate functions and the symbol 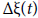 represents the jump of the function ζ at t, which is defined by
represents the jump of the function ζ at t, which is defined by 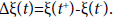
The theory of impulsive differential equations has become an important area of investigation in recent years stimulated by their numerous applications to problems arising in mechanics, electrical, engineering, medicine, biology, ecology etc [1-5].
Neutral functional differential equations with state- dependent delay and non-local conditions appear frequently in applications as model equations and for this reason the study of this type of equations has received great attention. The problem of the existence of solutions for second order functional differential equations with state-dependent delay and also nonlocal conditions have been treated in the literature recently in [6,7].To the best of our knowledge, the existence of solutions the impulsive second order abstract partial neutral functional differential equations with state-dependent delay and also nonlocal conditions is an untreated topic in the literature and this fact is the main motivation of the present work.
Preliminaries
Through this paper, A is the infinitesimal generator of strongly cosine function of bounded linear operators (C(t))t∈R on the Banach space (X,||.||). we denote by (S(t))t∈R the associated sine function which is defined by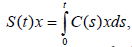 for x∈X and tR In the sequel, N and N are positive constants such that
for x∈X and tR In the sequel, N and N are positive constants such that 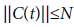 and
and 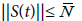 for every t∈I.
for every t∈I.
In this paper [D(A)] represents the domain of A endowed with the graph norm given by ||x||A=||x||+||ax||,
x∈D (A) while E stands for the space formed by the vectors x∈X for which C(.)x is of the class C1 on R. We know from Kisinsky [8-10], that E endowed with the norm 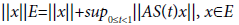 is a Banach space. The operator-valued function
is a Banach space. The operator-valued function
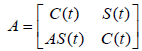 is a strongly continuous group of bounded linear operators on the space ExX generated by the operator
is a strongly continuous group of bounded linear operators on the space ExX generated by the operator 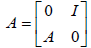 defined on D(A)xE. It follows from this that AS(t): E→X is a bounded linear operator and that AS(t)x→0,t→0, for each x∈E
defined on D(A)xE. It follows from this that AS(t): E→X is a bounded linear operator and that AS(t)x→0,t→0, for each x∈E
Furthermore, if x: (0,∞]→ X is a locally integrable function, then z(t) = ∫ S(t − s)x(s)ds, defines an E-valued continuous function. This is a consequence of the fact that
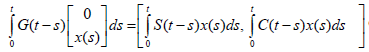 defines an ExX- valued continuous function.
defines an ExX- valued continuous function.
In this work we will employ an axiomatic definition for the phase space B. Specifically, B will be a linear space of functions mapping (-∞,0] into X endowed with a semi norm ||.||B and satisfying the following assumptions:
(A1) If x: (-∞,b]→X, b>0, continuous on [0, b] and x0B, then for every t[0, b] the following conditions hold:
(a) xt is in B
(b) ||x(t)||≤H||xt||B
(c) ||xt||B≤M(t)||x0||B+K(t) sup{||x(s)||: 0≤s≤t}we here H > 0 is a constant; K, M: [0, ∞)→{1, ∞), K is continuous, M is bounded and H,K,M are independent of x( . ).
(A2) For the functions x in (A1), xt is B valued continuous functions on [0,b].
(A3) The space B is complete.
Definition 2.1 (Mild solutions)
A function u: (-∞,a]→X is called a mild solution of the abstract Cauchy problem (1.1) – (1.3) for every s∈I and
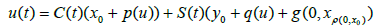
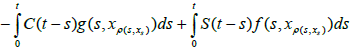
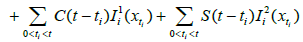
Some of our results is proved using the following well know results.
Theorem 2.2 (Leray Schauder Alternative)[4,pp,61]. Let D be a convex subset of a Banach space X and assume that 0∈D. Let G: D→D be a completely continuous map. Then the map G has a fixed point in D or the set {x∈D : x=λG(x),0<λ<1} is unbounded [11-14].
Theorem 2.3 Sadovskii [15] Let D be a convex, closed and bounded subset of a Banach space X. If F: D→D is a condensing operator, then F has a fixed point in D.
Remark 2.4 The function t→Ï•t is well defined and continuous from the set R(ρ-)=ρ (s,): (s,ψ)∈IxB, (s,ψ)≤0 in to B and there exists a continuous and bounded function JÏ•: R(ρ)→(0,∞) such that ||φt||B≤ J||φt||B for every t∈R(ρ).
Remark 2.5 The condition (2.4) is frequently verified by functions continuous and bounded. In fact, if B verifies axiom C2 in the nomenclature of [12], then there exists L < 0 such that
||φt||B≤L for every φ∈B continuous and bounded function. Consequently, 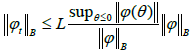 for every continuous and bounded function φ∈B and every t≤0. We also observe that the space
for every continuous and bounded function φ∈B and every t≤0. We also observe that the space 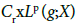 verifies axiom C2. In the rest of this paper, Ma and Ka are the constants defined by Ma=supt∈JM(t) and Ka= supt∈JK(t).
verifies axiom C2. In the rest of this paper, Ma and Ka are the constants defined by Ma=supt∈JM(t) and Ka= supt∈JK(t).
Using the following lemma for proof of our main result:
Lemma 2.6 [10,Lemma 2.1]
Let x:(-∞,a]→X be a function such that x0=φ and x[0,a]∈PC Then
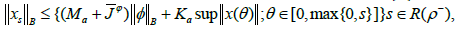 where
where 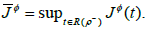
The terminology and notations are those general used in functional analysis. In particular, for Banach spaces Z,W, the notation L(Z,W) stands for the Banach space of bounded linear operators from Z into W and we abbreviate this notation to L(Z) when Z=W. Moreover Br(x,Z) denotes the closed ball with radius r > 0 in Z and for a bounded function x:[0,a]→X and 0≤t≤a we employ the notation ||xt|| for ||xt||=sup{||x(s)||: s∈[0,t]}
This paper has four sections. In the next section we establish the existence of mild solutions for the abstract Cauchy problem (1.1) - (1.3). In section 4 some applications are considered.
Existence of Solutions
In this section, we establish the existence of mild solution for the impulsive abstract Cauchy problem (1.1) – (1.5).
To prove our results, we assume that ρ: IxB→X is a continuous function and that the following conditions are verified.s
(H1) The function f: IxB→X satisfies the following properties,
(a) The function f(.,x):I→X is strongly measurable for every x∈B.
(b) The function f(t.,):B→X is continuous for each t∈I.
(c) There exist an integrable function mf: I→[0,∞) and a continuous nondecreasing function Wf: [0,∞)→ (0,∞) such that ||f(t,x)||B≤mf(t) Wf(||x||).)t,x)∈IxB.
(H2) g: IxB→X is continuous function and verifies the following conditions:
(a) There exists a continuous function mg: [0,∞)→ (0,∞) and a continuous nondecreasing function Wg: [0,∞)→ (0,∞) such that ||g(t,x)||B≤mg(t)Wg(||x||),(t,x)∈IxB
(H3) The maps Ij, Ji are continuous each function Ij is completely continuous and there are positive constants
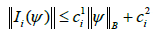
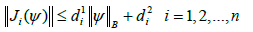
(H4) There are positive constants Pi,Qi such that
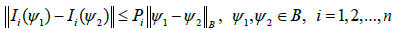
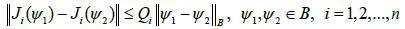
Theorem 3.1 Assume that the conditions (H1) – (H3) are verified and that g(.) is completely continuous. Suppose, furthermore that the following conditions hold:
(a) for every 0<t′ 0, the set U(t,t′,r)={S(t′)f(S,x): s∈{0,t],||x||≤r* is compact in X.
(b) p(.) is completely continuous and there is NP>0 such that ||p(u)||≤NP for every u∈C(I;X)
(c) for every s∈I and every r > 0 the set V(s,r)={S(s)q(x): ||x||≤r* is relatively compact in X and there is Nq>0 such that ||q(u)||≤ Nq for every u∈C(I;X)
if 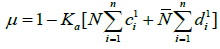 and
and
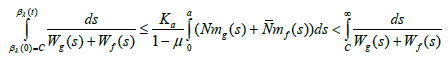
where
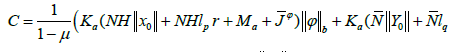
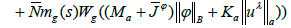
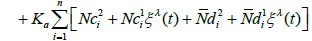
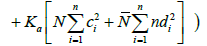
Then there exists a mild solution of (1.1) – (1.5).
Proof
On the space C(I; X) we define the map Γ: C(I;X)→C(I;X) by
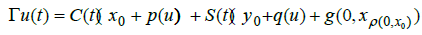
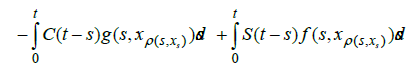
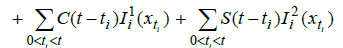
In order to use Leray Schauder alternative and from assumption (A1).
We obtain an a priori bounded for the solution of the integral equation u=λΓ(u), λ∈(0,1) if uλ is a solution of u=λΓ(u), λ∈(0,1)
we get,
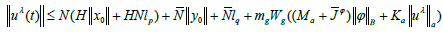
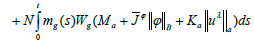
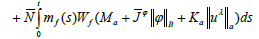
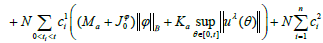
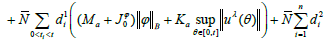
Denoting by the βλ(t) right hand of above equation follows that,
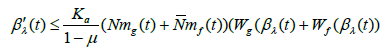
and hence,
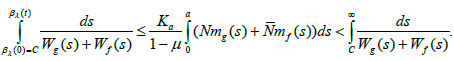
Which implies that the set of function {βλ(.):λ∈(0,1)} is bounded in C(I; R). This prove that {Uλ(.):λ∈(0,1)} is also bounded in C(I; X).
Next, we prove that Γis completely continuous. To this end, we introduce the decomposition Γ=Γ1+Γ2+Γ3 where,
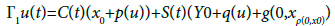

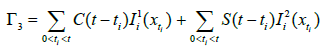
It is easy to show that Γ1 is completely continuous and that Γ2 is continuous. Next, by using Ascoli Arezela we prove that Γ(Br(0,C(I;X))) is relatively compact C(I;X). In the sequel Br=Br(0,C(I;X)).
Step:1
The set Γ2(Br={Γ2u:u∈Br} is equicontinuous on I. Let t∈I and g(.) is completely continuous, there exist δ>0 such that
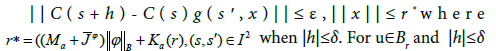
with t+h∈I, we get
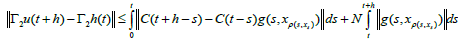
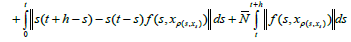
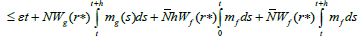
which prove the assertion.
Step:2
The set Γ2(Br)(t)={Γ2u(t):u∈Br} is relatively compact in X for every t∈I Let t∈I and ε>0 If u∈Br, x∈Br from the estimate, ||f(θ,u(θ))||≤mf(θ) wf(||u(θ)||)≤mf(θ)wf(r*) follows that the set U={f(t-s),x(ts); s∈{0,t},u∈Br}is bounded in X. Using that S:I→L(X) is uniformly Lipschitz on I, we can chose 0= S1<S2<…<Sk=t such that ||S(sʹ)y-S(s) y||<É›, y∈U, where S,sʹ∈[Si, Si+1] for some i = 1,2,…,k-1. Let x∈Br Bocher integral see [13,lemma 2.1.3] and fact that V={C(s)g(sʹ,x)} is relatively compact in X, follows that,
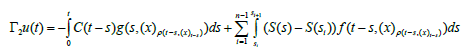
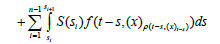
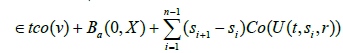
where co(Q) denote the convex hull of a set Q. Thus Γ2(Br)(t) is relatively compact in X. From the steps 1 and 2, follows that Γ2(Br) is relatively compact in C(I; X) and so that Γ2 is completely continuous. Finally, the theorem 1.1 assert that Γ has a fixed in C(I; X). The proof is complete.
If the maps g,p,q fulfill some Lipschitz conditions instead of the compactness properties considered in the preceding theorem, we also can establish a result of existence.
Theorem 3.2
Assume that (H1) and (H4) are verified and that the following conditions hold;
(a) for every 0<tʹ 0, the set U(t, tʹ,r)={S(tʹ)f (s,x): s∈[0,t]} is relatively compact in X.
(b) There exists positive constants lg,lp and lq such that,
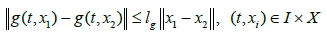
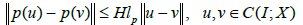
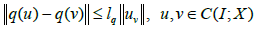
and
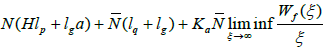
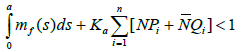 (3.1)
(3.1)
Then there exists a mild solution of (1.1) – (1.5).
Proof
Let Y=C(I;X) and Γ= Γ1+Γ2+Γ3: Y→Y be the map defined by
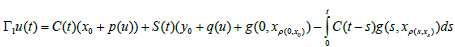
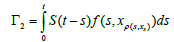
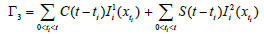
We affirm that there exists r > 0 such that Γ(Br(0,Y))⊂ Br(0,Y) In fact, if we assume the affirmation is false, then for each r > 0 there exists ur∈Br(0,Y) such that ||Γ ur ||>r. which imply that
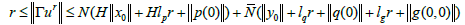
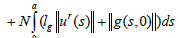
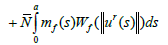
and so that
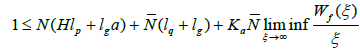
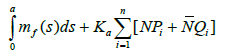
which is an absurd.
Step:1
Let r0>0 such that Γ(Br(0,Y))⊂ Br0(0,Y) using the steps in the proof of theorem (3.1), follows that Γ2 is completely continuous and from the estimate
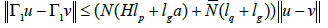
such that Γ1 is a contraction.
Step:2
The map Γ3 is a contraction on Br(0,Y). The assertion follows directly from (3.1) and the estimate,
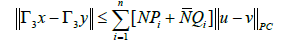
Thus, Γ is a condensing map on 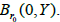 The assertion is now consequence of the Sadovskii’s point theorem, see [15,16].
The assertion is now consequence of the Sadovskii’s point theorem, see [15,16].
The proof is finished.
Conclusion
In this section we consider the applications of our abstract result.
We discuss the existence of solutions for the partial differential system with state-dependent delay and nonlocal conditions:
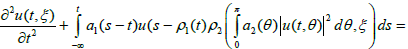
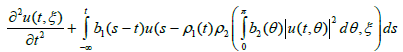 (4.1)
(4.1)
for t∈I=[0,a],ξ∈[0,π], subject to the nonlocal conditions
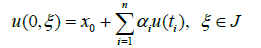 (4.2)
(4.2)
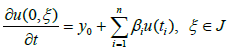 (4.3)
(4.3)
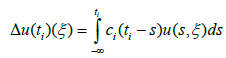 (4.4)
(4.4)
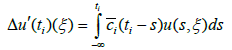 (4.5)
(4.5)
where 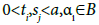 and
and  are fixed numbers
are fixed numbers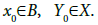 By the definition of the functions
By the definition of the functions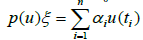 and
and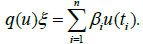 The system (4.1) – (4.3) can be described as the abstract Cauchy problem with state-dependent delay and nonlocal conditions. To apply our abstract results, we consider the space
The system (4.1) – (4.3) can be described as the abstract Cauchy problem with state-dependent delay and nonlocal conditions. To apply our abstract results, we consider the space 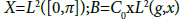 and the operator Af=fʹʹ with domain
and the operator Af=fʹʹ with domain
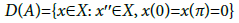
It is well known that A is the infinitesimal generator of a strongly continuous cosine function (C(t))t∈R on X. Furthermore, A has a discrete spectrum, the eigen value are –n2, n∈N, with corresponding eigen vectors the following properties hold
(a) The set {Zn: n∈N}is an orthonormal basis of X.
(b) For 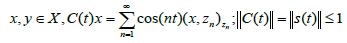 for all t∈R and that S(t) is compact for every t∈R
for all t∈R and that S(t) is compact for every t∈R
(c) If Φ is the group of translations on X defined by 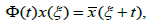 where
where  is the extension x with period 2π, then
is the extension x with period 2π, then 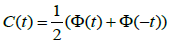 and
and 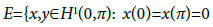 see [4] for details.
see [4] for details.
(d) The function ci∈C([0,∞);R) and 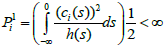
(e) The function 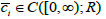 and
and 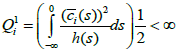
Assume that φ∈B the functions ai: R→R, b:i R→R, and ρi: [0,∞)→ [0,∞), i=1,2 are continuous, a2(t)≥0 and b2(t)≥0 for all t≥0 and 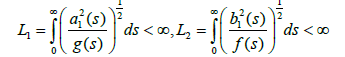
Under these conditions we can define the operators f: IxB→X; g: B→X and Ii,Ji:B→X and ρ: IxB→R by
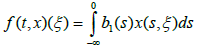
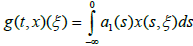
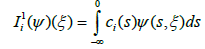
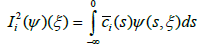
and transform system (4.1) – (4.5) in to the abstract Cauchy problem (1.1) – (1.5). Moreover f is a continuous linear operator with ||f||≤L1,||g||≤L2,ρ, is continuous and ρ(t,ψ)≤s for every S∈[0,a]. ||f(t,ψ)||≤d1(t)+d2(t)||ψ||B for every t∈[0,a] where
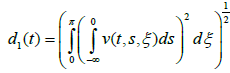 and
and 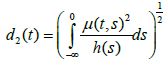
Case(i) Assume that φ satisfies (Remark 2.4). Then there exists a mild solution of (4.1) – (4.5).
Case(ii) If φ is continuous and bounded, then there exists a mild solution of (4.1) – (4.5)
References
- Benchora M, Ntonyas SK (2002) Existence of mild solutions of second order initial value problems for delay integrodifferential inclusions with nonlocal conditions. Math Bohem 127: 613-622.
- Benchora M, Ntonyas SK (2001) Existence of mild solutions of second order initial value problems for differential inclusions with nonlocal conditions. Atti Som Mat Fis Uni Modena 2: 351-361.
- Benchora M, Ntonyas SK (2000) Controllability of second-order differential inclutions in Banach spaces with nonlocal conditions. J Optim Theory Appl 107: 559-571.
- Deimling K (1985) Nonlinear functional analysis, Springer-Verlag, Courier Corporation, USA.
- Fattorini HO (1985) Second order linear differential equations in Banach spaces, North-Holland Mathematics Studies, North-Holland, Amsterdam, USA.
- Hernandez E (2007) Existence of solutions for a second order abstract functional differential eqution with state-dependent delay. Electron J Diff Eqns 21: 1-10.
- Hernandez E, Mauricio LP (2005) Existence results for a second order abstract Cauchy problem with nonlocal conditions. Electron J Diff Eqns 73: 1-17.
- Hernandez E (2003) Existence of solutions to a second order partial differential equation with nonlocal conditions. Electron J Diff Eqns 51: 1-10.
- Hernandez E, Mckibben M (2007) On state-dependent delay partial neutral functional differential equations. App Math Comput 186: 294-301.
- Hernandez E, Prokopczyk A, Ladeira L (2006) A note on state dependent partial functional differential equations with unbounded delay. Nonlin Anal RWA 7: 510-519.
- Hernandez E, Pierri M, Uniao G (2006) Existence results for a impulsive abstract partial differential equation with state-dependent delay. Comput Math Appl 52: 411-420.
- Kisynski J (1972) On cosine operator functions and one parameter group of operators. Studia Math 44: 93-105.
- Martin RH (1987) Nonlinear operators and differential equations in Banacha spaces, Robert E Krieger publ Co, Florida, USA.
- Pazy A (1983) Semigroups of linear operators and applications to partial differential equations, Springer Science & Business Media, New York, USA.
- Sadovskii BN (1967) A fixed-point principle. Funct Anal Appl 1: 151-153.
- Hino Y, Murakami S, Naito T (1991) Functional-differential equations with infinite delay. Lecture notes in Mathematics, Springer-Verlag, Berlin.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi 