Research Article, J Nucl Ene Sci Power Generat Technol Vol: 5 Issue: 4
Fluid Dynamics in Parallel Helical Pipes
| Cristina Bertani, Mario De Salve and Bruno Panella* | |
| Politecnico di Torino, Department of Energy, Italy | |
| Corresponding author : Bruno Panella
C. so Duca degli Abruzzi 24, 10129 Torino, Italy E-mail: bruno.panella@polito.it |
|
| Received: May 09, 2016 Accepted: June 20, 2016 Published: June 24, 2016 | |
| Citation: Bertani C, De Salve M, Panella B (2016) Fluid Dynamics in Parallel Helical Pipes. J Nucl Ene Sci Power Generat Technol 5:4. doi:10.4172/2325-9809.1000158 |
Abstract
Single phase and air-water two-phase flow in 12 mm inner diameter parallel helical pipes are investigated with three different coils diameters. Flow rate distribution, pressure drops and void fraction, along the pipes in the parallel channels are measured. The test pressure drops are compared with theoretical ones, in terms of friction factors and two phase multipliers. The instabilities arisen during the experimental tests are investigated and are related to the void fraction and flow quality. The void fraction values corresponding to the onset of oscillations are compared with a modified RELAP5/MOD3.3 code results at the same fluid dynamic conditions. Then the density wave, the flow pattern and parallel channel oscillations in some simple cases like a single vertical heated channel and in parallel channels, have been predicted by RELAP5/MOD3.3, to investigate the code ability to predict instabilities and to get instability maps for such cases; in particular the stability of the helical steam generators designed for Small Modular Reactors is investigated.
Keywords: Helical pipes; Pressure drops; Two phase flow; Fluid dynamic instability; RELAP5/MOD3.3 code
Keywords |
|
| Helical pipes; Pressure drops; Two phase flow; Fluid dynamic instability; RELAP5/MOD3.3 code | |
Introduction |
|
| Helical pipes steam generators have been adopted in the past for different nuclear power plants, as gas-cooled reactors (Advanced Gas Cooled, HTGR) and SuperPhénix fast reactor (sodium cooled), and are designed for the advanced nuclear reactors, that are likely to be deployed in the next future, in particular for Small Modular Reactors. The two-phase flow investigation in helical pipes is important to improve the performance of the steam generators, regarding heat transfer, fluid dynamics and instability; therefore experimental data can help to obtain a better design and to validate theoretical models. Some authors have carried out experiments on the fluid-dynamics in helical pipes: Xin et al. [1] used an air- water mixture; Santini et al. [2,3] investigated the transition between laminar and turbulent flow by means of water and vapour; Colombo et al. [4] performed a study about the fluid dynamic instabilities in helical pipes. Kakac [5] classified them in terms of static and dynamic instabilities or also in terms of pure or composed ones. Density wave oscillations (DWO) were studied for the first time by Stenning [6]. As suggested by Fukuda [7], parallel channel instabilities seem to be similar to DWO in a single heated channel, that are always due to a variation of flow parameters like pressure drop. Stability maps are a powerful tool to predict the onset of instabilities in fluid dynamics systems and many authors have developed stability maps, either in a theoretical way or by experiments. Yun et al. [8] proposed both a theoretical and an experimental study, whereas Papini et al. [9] performed a comparison of the stability maps obtained experimentally with the RELAP5/ MOD3.3 [10] code prediction in helically coiled parallel channels. In the present paper an experimental investigation about single-phase and two-phase flow in three parallel helically coiled pipes is presented by using an air-water mixture at different flow qualities for every pipes. The flow distributions void fraction and pressure drops are measured at each total mass flow rate. The void fraction values that are measured in correspondence to the onset of instability are compared with the values predicted by a modified RELAP5/MOD3.3 code. The instability analysis by means of this system code has been extended to predict the density wave oscillations, flow pattern oscillations and parallel channel oscillations in some simple cases, like a single vertical heated channel and in parallel channels, both in vertical and inclined layout. In particular the stability maps of the helical steam generators designed for nuclear reactors, with reference to the Small Modular Reactor, are presented. | |
Experimental Facility |
|
| An open tank is connected to three parallel helical pipes by means of two headers (Figures 1 and 2A). Water is driven by a centrifugal pump through an horizontal pipe to the single phase cylindrical header, that is connected to 4 branches; the first one is linked directly with the water tank, whereas the others are disposed in symmetrical way with an angle of 120°. These three branches (Figure 2B) are horizontal and constitute the inlet of the three vertical parallel helically coiled channels that have different geometrical parameters in order to simulate the behaviour of a real steam generator with different length, pitch and turns. The three horizontal branches are all equipped with a flow meter. The two-phase flow is provided by a mixer device that is located at the inlet of each helical pipe. The facility scheme is shown in Figure 1 and the main geometrical parameters are reported in Table 1. Straight pipes of 8 mm inner diameter are located between the outlet of the coils and the inlet of the two phase flow header. The instrumentation consist of 13 differential pressure transducers in the range of 0-130 kPa and with 0.1% of full scale accuracy, an absolute pressure transducer in the range 0-0.7 MPa and with 0.1% of full scale accuracy, an orifice flow meter for the liquid flow rate with 2.5% of full scale accuracy and 2 rotameters for the air flow rate with accuracy of 5% full scale. The total liquid flow rate is measured by a rotameter in the range (0.44 – 4.4) kg/s with 1% of full scale accuracy. | |
| Table 1: Geometrical parameters. | |
| Figure 1: Facility scheme. | |
| Figure 2a: Facility picture (one of the three parallel helical pipes is shown). | |
| Figure 2b: Facility picture (the horizontal branches at the inlet of the three helical pipes are shown). | |
Single Phase Flow Results |
|
| The first tests have been carried out in single-phase flow; this approach is necessary to calibrate the instrumentation and to evaluate the flow rate distribution and pressure drops both in the horizontal channels and in the helically coiled pipes. These tests are performed by varying the total flow rate in the three parallel channels in order to get several flow conditions in the range of total flow rate between 0.45 kg/s and 0.6 kg/s; the ratio between the flow rate in a single channel and the total flow rate is kept constant for each channel (Table 2). | |
| Table 2: Flow rate ratio. | |
| The flow rate ratio is lower as the length increases, due to the hydraulic resistance which increases with the length. The hydraulic resistance depends on several geometrical parameters like diameter, length, roughness and the total length. The loop pressure drops is expressed by Equation 1: | |
| The pressure drops are measured both in the horizontal branches (Figure 3) and in the helical pipes (Figure 4). | |
| Figure 3: Pressure drops in the three horizontal branches. | |
| Figure 4: Pressure drops in the helical pipes. | |
| The pressure drops increase with the mass flux following a power law with an exponent of about 1.64 in the horizontal branches. | |
| This exponent can be explained by considering that the friction factor in case of turbulent flow depends on Re−m, which leads to pressure drop dependence as expressed in Equation 2. | |
| The value of the m coefficient depends on the correlation that is chosen for the friction factor; if the Blasius and Ito correlations are adopted, m is 0.25. Figure 3 shows the pressure drops in the helically coiled pipes as a function of the mass flux: several measurements that are obtained in the same loop are presented in order to check the repeatability of the results. The difference ξ=2-m is a function of the friction factor and in the case of helical pipes is about 0.5 (Figure 4). Looking at the results shown in the Figure 3, the pressure drops values in the second and third helically coiled pipes are consistent with the ones obtained by Castiglia et al. [11] while the pressure drops measured in the first helical channel seems to be a little underestimated. However, even in this case, it is clear a parabolic behaviour of the pressure drops in agreement with the correlations. In order to compare the single-phase flow experimental results with the correlations, the Reynolds numbers from the test data are used to calculate the Fanning friction factors and then the pressure drops by means of the correlations. The Reynolds number is evaluated from the flow rate measured in the channels (Equation 3). | |
| The Fanning friction factor is evaluated by means of the Blasius and Ito correlations for turbulent flows, as reported in Equations 4 and 5. | |
| With: |
|
| The friction factor is used to evaluate the pressure drop through the Equation 6: | |
| As shown in Figure 5, some experimental data are lower than Blasius data of a straight pipe. This results agree with the findings of Santini et al. [3] which introduce a depression zone where the pressure drops in helical pipe are lower than the pressure drops in the straight pipe at the same flow rate. | |
| Figure 5: Pressure drops in the helical pipes compared with Blasius and Ito correlations. | |
Two-Phase Flow Results |
|
| Experimental procedure | |
| The experimental procedure consists in establishing the twophase flow only in one channel, while the two others are in single phase flow condition, in order to simplify the operations; so compressed air is injected in a single channel through the mixer and, as a consequence, the water flow rate splits in the three channels to get the same pressure drops in all parallel channels. The test runs are carried out by varying the flow rate in each channel; the range of Dean number in the different tests is shown in Table 3. | |
| Table 3: Dean number in test data. | |
| The liquid flow rate ratios with respect to the total liquid flow rate versus the superficial air velocity in the channel with two phase flow, are presented in Figure 6: the channel 2 has a different behaviour with respect to the others because, for two-phase flow, the water flow rate in that channel is larger than in the others. | |
| Figure 6: Water flow rate ratio between single channel and total flow rate in parallel helical pipes. | |
| Void fraction measurements | |
| In the tested flow quality range (up to 0.08) typical slug and churn flow patterns have been observed. The void fraction is evaluated by means of the “weight method”, by comparing the amount of water either for single-phase flow or for two-phase flow inside the helically coiled pipes. The void fraction as a function of the flow quality is reported in Figure 7: at low quality values the increase of the void fraction is quite large due to the slug flow pattern occurrence, whereas at larger quality values the void fraction becomes more stable in correspondence of an annular flow pattern. | |
| Figure 7: Void fraction against flow quality in parallel helical pipes. | |
| Pressure drops measurements | |
| The two-phase flow pressure drops values measured in the helically coiled pipes are used to get the two-phase multipliers: the test data are compared with the Xin [12] correlation that takes into account also the effects due to the curvature of the pipes (Equations 7 and 8, where Fr is the Froude number as reported in Equation 9). | |
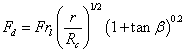 (8) (8) |
|
| The Froude number for the experimental data varies from a minimum value for the first channel up to 25.6 for the second one. The comparison between the experimental multiplier and that predicted by the Xin correlation is shown in Figure 8. The results show that the Xin model correlates the two phase multiplier experimental values within 40% at a confidence level of 75 %. | |
| Figure 8: Comparison of the two-phase multiplier between present experiments and prediction by Xin. | |
| Another comparison is performed between the measured pressure drop and the one predicted by Shannak [13], who evaluated from the Reynolds number (Equation 10) the two-phase friction factor (Equation 11), which determines directly the two-phase pressure drop. | |
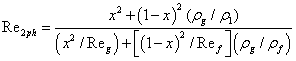 (10) (10) |
|
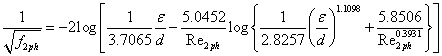 (11) (11) |
|
| There is a poor agreement with the experimental results likely due to the lack of dependence on the helical diameter in the Shannak formulation. | |
Fluid Dynamic Instability |
|
| Measurements for air water two phase flow and comparison with RELAP5/MOD3.3 code | |
| Some tests have experienced the arising of flow rate oscillations in the helical test section with two-phase flow and, as a consequence, also in the other two helical pipes in which there are single phase flow. Frequency, void fraction and flow quality when the oscillations occur are reported in Table 4. In correspondence of the onset of the instability, the void fraction and the flow quality are evaluated; the aim is to identify some critical or limit conditions for which oscillations arise. Looking at the experimental data, a boundary zone is identified at void fraction ranging from 0.7 to 0.8. At void fraction values lower than 0.7 there are no oscillations, whereas for values higher than 0.8 all the tests experience a certain flow rate oscillation. This behaviour suggests that the oscillations are due to the “flow pattern instability” because they are clearly related to the flow pattern transition. More in detail, in case of oscillations, the flow pattern is a fully developed slug flow type, as shown in Figure 9. | |
| Table 4: Onset of oscillation. | |
| Figure 9: Slug flow picture. | |
| The void fraction values that are measured in correspondence to the onset of instability are compared with the values predicted by RELAP5/MOD3.3 code. The aim is to understand if the code is able and reliable to predict the instability, even if one-dimensional. For this analysis the facility has been simulated with three parallel channels that are inclined to simulate the difference between the three helically coiled pipes, but, of course, because of the onedimensional structure of the code, the effects due to the curvature and the secondary flows have been neglected. The comparison between the void fraction predicted results and the experimental ones at the instability onset is shown in Figure 10: the results show that the all the points are correlated within 20%. | |
| Figure 10: Comparison of the void fraction at the instability onset between present experiments and prediction by RELAP5/MOD3.3. | |
Concluding Remarks |
|
| An experimental campaign has been carried out to study the fluid-dynamics in parallel helically coiled pipes. The comparison between the Xin model and the two phase multiplier experimental values shows that it correlates the data within 40% at a confidence level of 75 %. The experimental tests have highlighted the importance of the instability phenomena for certain conditions at high void fraction (Table 5); in particular, in case of a non-heated pipe, the flow pattern instability determines very strong flow rate oscillations with an amplitude up to ± 100% of the average flow rate. The flow pattern instability in a single two-phase channel determines the flow rate oscillations also in the other single-phase channels (parallel channel instability). The comparison of the test data with the results of modified RELAP5/MOD3.3 code shows that, the prediction of the onset of the flow pattern instability is rather good with all test values of the void fraction that are correlated within 20 %. The approximation used for helically coiled pipes in the multichannel systems seems not to affect the instability onset and it seems a rather powerful tool for the fluid dynamic instability prediction. | |
Acknowledgment |
|
| This research has been supported by ENEA. The authors thank the high quality technical team of Politecnico di Torino Department of Energy and in particular R. Costantino and G. Vannelli. | |
References |
|
|
|
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi